分布式光伏发电系统接入城市配电网的优化配置研究

卢 佳，李 涛

(国网浙江省电力公司杭州供电公司，杭州市310009)

0 引 言

由于能源危机和环境保护问题，包括新能源及可再生能源的分布式发电在电力能源工业中日益受到关注。城市配电网作为大电网的有机组成部分，直接关系到主动配电网和智能电网发展的安全性和可靠性，具有显著的综合经济效益。因此，合理规划城市配电网能够更好地实现电力系统的安全、经济、可靠和稳定，保证系统高效运行。为求解光伏发电系统接入配电网的电源规划问题，国内外学者引入人工智能算法，并展开广泛的研究［1-4］。

粒子群优化(particle swarm optimization，PSO)是一种基于集群智能的随机优化算法，由Kennedy 和Eberhart 于20世纪90年代提出。该算法基于鸟群觅食行为，在多维空间中构造粒子群进行寻优，每个粒子通过统计迭代过程中自身和群体发现的最优值修正自己的前进方向和速度［5］。由于该算法操作简便，依赖的经验参数较少，已成功运用于求解多维非线性函数优化［6］。在电力系统中，PSO 已被用于求解输电网扩展规划［7］、机组容量优化组合［8］、无功最优潮流［9］以及补偿电容器优化配置［10］等问题。

1997年，Kennedy 和Eberhart 又提出了改进形式的PSO 算法，即二进制粒子群优化算法BPSO(Binary PSO)［11］，并成功将其应用于求解离散优化问题。在二进制粒子群中，粒子的速度向量不再是粒子位置的变化率，而是粒子位置改变的概率。速度向量表示粒子以某一概率确定是1 状态还是0 状态。根据速度的大小来选择粒子在对应位置上为1 或0。但是，当速度更新公式中含有0 的分量较多，则粒子速度的修正程度将减小，种群多样性大大减弱，影响算法的全局搜索能力［12］。

因此，本文采用有功、无功网损微增率来确定光伏发电系统的接入位置，提出综合微增率，通过计算综合微增率来确保城市配网系统的网损最小。同时本文提出一种配电网接入光伏发电系统的多目标规划方法，充分考虑不可控光伏发电功率、负荷的不确定性，以光伏发电系统的经济成本、网损、环境和电压质量4个方面的指标为评价指标构成多目标的函数，并提出带辅助搜索空间的BPSO 算法进行求解，并通过IEEE－30 系统进行仿真验证。仿真结果表明:采用该方法能够实现配网系统的合理优化配置，从而保证城市配电网的稳定、可靠、安全运行。

1 城市配电网中光伏发电系统优化布置

若设配电网中任何一条支路i-j 的有功网损为

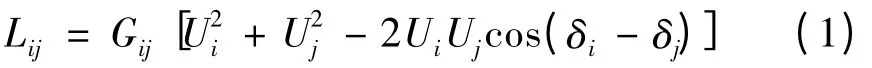
式中:Gij为节点i 与j 之间的节点导纳矩阵元素的实部;Ui，Uj分别为节点i 与j 的电压幅值;δi，δj分别为节点i 与j 的电压相角。

设配电网内总节点数为N，则配网系统中总有功网损为

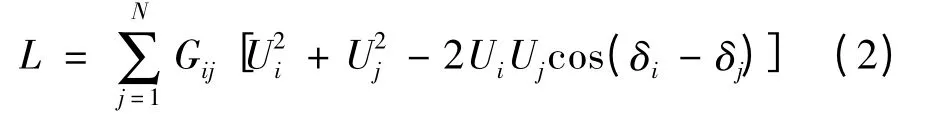
通过对公式(2)求一阶偏导，可得:

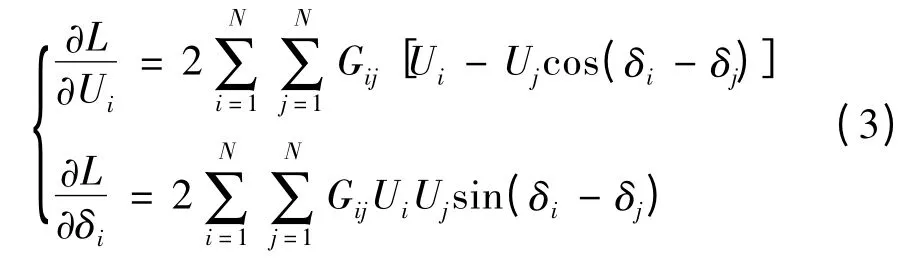
则根据对公式(3)整合，可得:

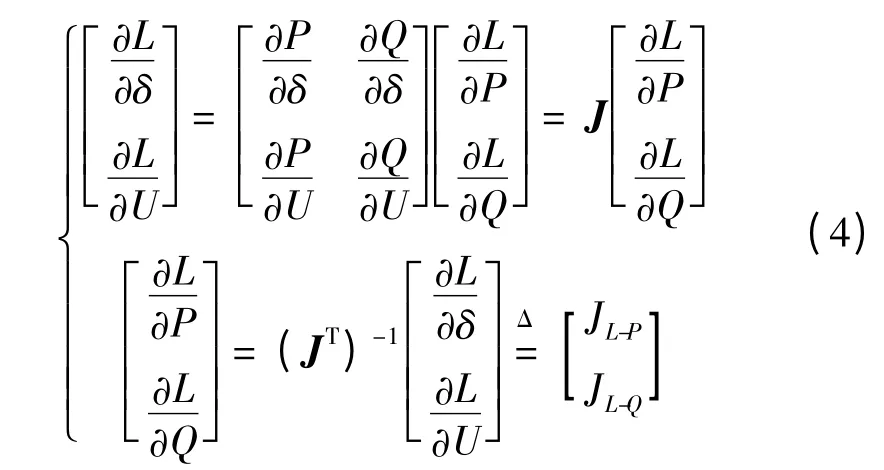
式中:J 为雅可比矩阵;P，Q 分别为节点的有功和无功功率。从而进一步得出配电网系统的各节点有功和无功网损微增率(分别为kPi和kQi)为

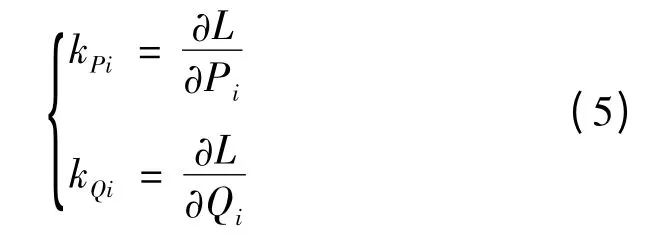
网损微增率是指在系统中节点i，由于系统中单位负荷的增加而导致的系统的网损增加量，即对网损的贡献率。如果节点的网损微增率数值为负，说明在此节点从电网汲取功率，这样有利于降低网损;如果节点的网损微增率数值为正，则相反。因此，考虑到节点有功、无功负荷对网损的贡献率，综合网损微增率综合了节点有功、无功负荷对有功网损的贡献，假设θi为节点i 的功率因数角，计算得节点i 的综合网损微增率dLi:

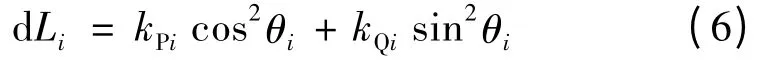
在配电网中针对光伏发电系统的接入，通过对综合网损微增率的大小排序，说明在此节点从电网汲取功率较大，有利于网损的降低。

2 光伏发电系统的容量优化

2.1 光伏发电系统的经济成本指标

针对光伏发电系统的经济成本，本文主要考虑光伏发电系统的年售电收益、初始投资成本的年金现值和年运行与维护成本［13-15］。经济成本指标主要是通过比较年售电收益与初始投资成本的年金现值和年运行与维护成本之间的差值，这样能看出光伏发电系统具有一定的经济性，保证系统的经济运行。

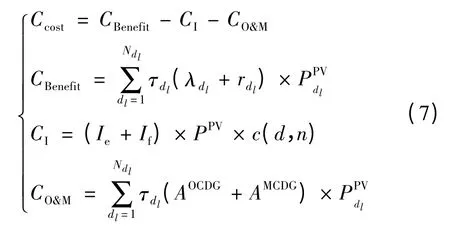
式中:Ccost为光伏发电系统的经济成本;Cbenefit为光伏发电系统的售电收入;CI为初始投资年金现值;CO＆M为光伏发电系统的年运行与维护费用;Ndl为调度时段;τdl为第dl个调度时段的时间;λdl、rdl分别为第dl个调度时段的电价，电价补贴;Vl为光伏发电系统在第dl个调度时段的售电量;Ie，If分别为光伏发电系统单位容量的购置成本和安装成本;c(d，n)为年金现值系数;PPV为光伏发电系统的额定装机容量;AOCDG、AMCDG分别为光伏发电系统的单位发电量的运行成本和维护成本。

2.2 光伏发电系统的网损指标

光伏发电系统的网损指标主要是对比装设光伏发电系统与未安装光伏发电系统的比值，这样能有效对比系统的降损收益，改善电压水平，提高系统的稳定性，保证系统的供电可靠性。假设某配电网中含有N个节点，并有N－1个馈线，因此，配网中的网损功率为

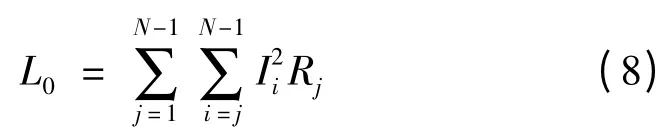
式中:L0为配电网的初始网损;Ii为第i 段馈线的电流值;Rj为第j 段馈线的电阻值。

同时，若将K 点定义为光伏发电系统的接入点，则假设光伏发电系统的节点注入电流为IPV(K)，因此引起的功率损耗为

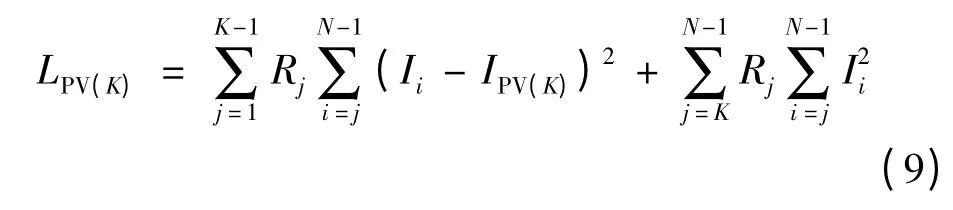
得到光伏发电系统的网损指标为

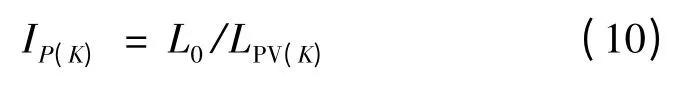
通过比较光伏发电系统安装前后的网损变化情况，能够更好地得出光伏发电系统带来的网损效益，实现光伏发电系统的综合经济效益。

2.3 光伏发电系统的环境指标

与消耗石油、煤炭、天然气等传统化石燃料发电相比而言，光伏发电系统几乎不会排放污染气体，具有较大的社会效益，能够解决当前日益严重的雾霾天气，对维护国家能源安全也具有战略性的意义。因此，本文中的环境指标，主要为未安装PV 和安装PV后排放的污染气体量的比值。这样通过环境指标的对比，可以看出光伏发电系统的接入可以有效地降低二氧化碳、二氧化硫以及氮氧化合物的排放，节能减排，是一种环保友好的新能源发电方式。

第i 种环境污染物的排放量为

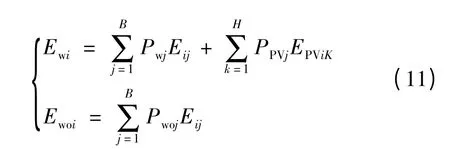
式中:B 为配电网中的传统火电机组的台数;H 为配电网中安装的PV 台数;Pwj和Pwoj分别为传统火电机组在安装PV 装置时和未安装PV 装置时的发电出力;Ewi、Ewoi分别为传统火电机组的第i 种污染物在安装PV 装置时和未安装PV 装置时的污染物排放量;Eij、EPViK为第i 种污染物单位发电的污染物排放量和PV 的单位排放量，由于PV 装置是节能环保装置，因此EPViK一般取0。

第i 中污染物的环境指标为

式中:IEi为第i 中污染物的环境指标，一般都大于1。

但是由于传统火力发电机组会向大气中排放多种污染气体，因此，本文给出了综合环境指标IE，为

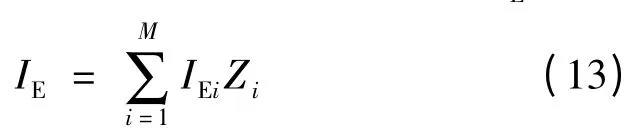
式中:M 为传统火力发电机组污染物排放种类的总数;Zi为第i 种污染物的权重排放因子，而且应该满足以下条件:

2.4 光伏发电系统的电压质量指标

光伏发电系统接入城市配电网会改善线路的电压参数，提高系统的电压质量。因此，本文考虑的电压质量指标主要是对比安装PV 装置时与未安装PV装置时的线路电压幅值，从而更加直观地看出装设了PV 装置后能够显著地提高系统的节点电压，保证电力系统对电压质量的基本要求，确保用户的安全用电。假设某配电网中含有N个节点，第i个节点的节点电压为Ui，负荷为Wi，权重系数为ki，因此电压质量指标为

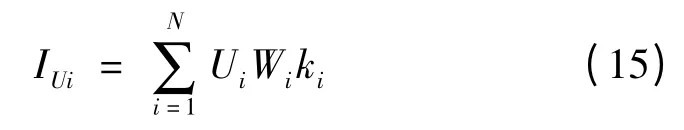
式中IUi为第i个节点的电压质量指标。

本文充分考虑的电压质量改善指标为安装PV装置时与未安装PV 装置时的线路电压幅值的比值，即

式中:IUoi、IUwi分别为安装了PV 装置和未安装PV装置时的线路电压质量的指标。

2.5 优化配置模型以及约束条件

2.5.1 优化配置模型

本文提出一种配电网接入光伏发电系统的多目标规划方法，以配电网运营商规划期的经济成本、网损、环境和电压质量4个方面的指标为评价指标构成多目标函数，结合式(7)、(10)、(13)、(16)得出目标函数为

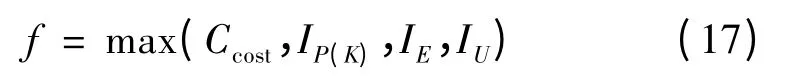
2.5.2 功率平衡约束

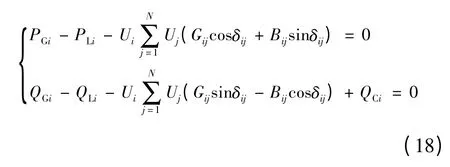
本文考虑的约束条件主要是节点潮流约束，由于光伏发电系统的接入会改变系统的节点潮流流向，因此潮流约束平衡是必须考虑的，即式中:PGi、PLi分别为发电机的有功功率的发电出力和负荷大小;QGi为发电机的无功功率;QLi为无功负荷;Ui为系统的节点电压;δij为节点电压的相角差。2.5.3 不等式约束条件

本文考虑的不等式约束包括发电机的发电功率极限、电压约束、线路的传输功率约束以及穿透功率约束，即

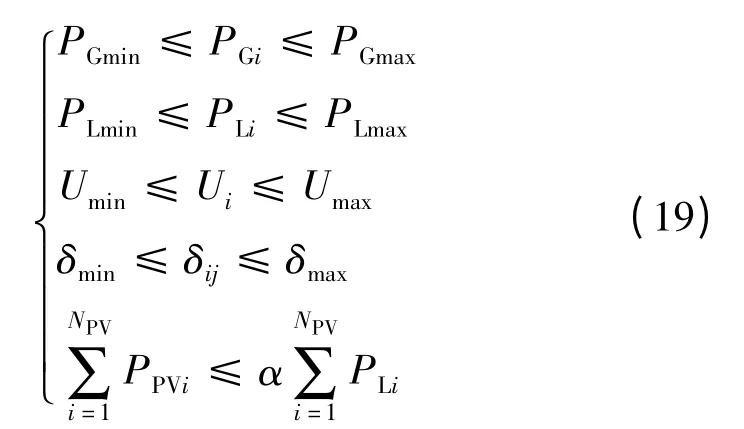
3 改进BPSO 算法

3.1 传统BPSO 算法

二进制粒子群算法是在基本粒子群算法的基础上提出的，适用于离散空间优化问题［16］。在二进制粒子群中，粒子速度和位置更新公式分别为

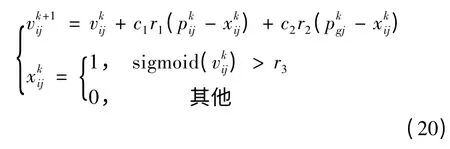
式中:

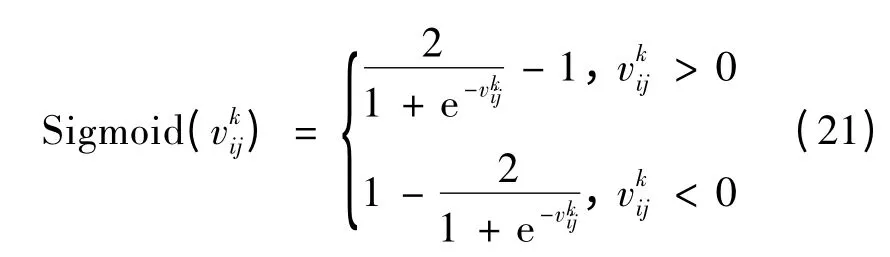
3.2 带辅助搜索空间的BPSO 算法

为了提高粒子的搜索性能，考虑既保留了在连续空间搜索中PSO 所具有的明显优势，又适用于离散空间优化问题，构造一个与解空间Y 同维的辅助搜索空间Y'，Y'⊂Rn，则粒子的位置由解空间Y 中的n 维向量Xi和辅助搜索空间Y'的中的n 维向量Xi'(称之为粒子的辅助位置)共同表示。基于这个辅助搜索空间，种群第i个粒子可由(Xi，Xi'，Pi，P'i，Vi)表示，其中:

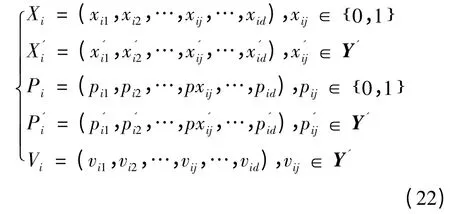
速度更新公式和位置更新公式分别为

粒子个体最优位置和粒子个体最后辅助位置更新公式为

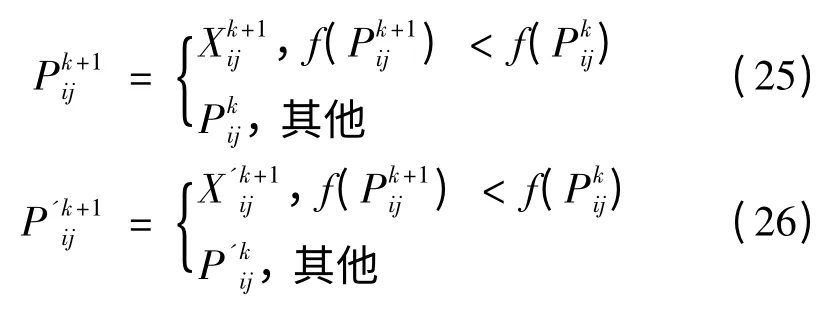
4 算例仿真

4.1 算例介绍

本文采用典型算例IEEE 30 节点系统进行仿真分析，并采用Matlab2012 进行编程计算，IEEE 30 节点系统如图1 所示。节点系统中包括了6 台发电机系统和4个无功补偿装置，其中当地的气候条件、光照强度等如图2 所示，图3 为实时电价曲线，由于采用新能源并网发电，国家发改委规定光伏上网电价为1.11元/(kW·h)。同时系统中的有功负荷为272.8 MW，无功负荷为124.3 MW，其中调度时段见表1，光伏发电系统的设备参数见表2。

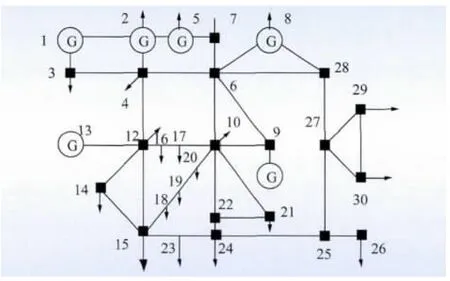
图1 IEEE 30 节点原理图Fig.1 IEEE 30 structure

图2 当地的光照强度曲线图Fig.2 Local light intensity curve

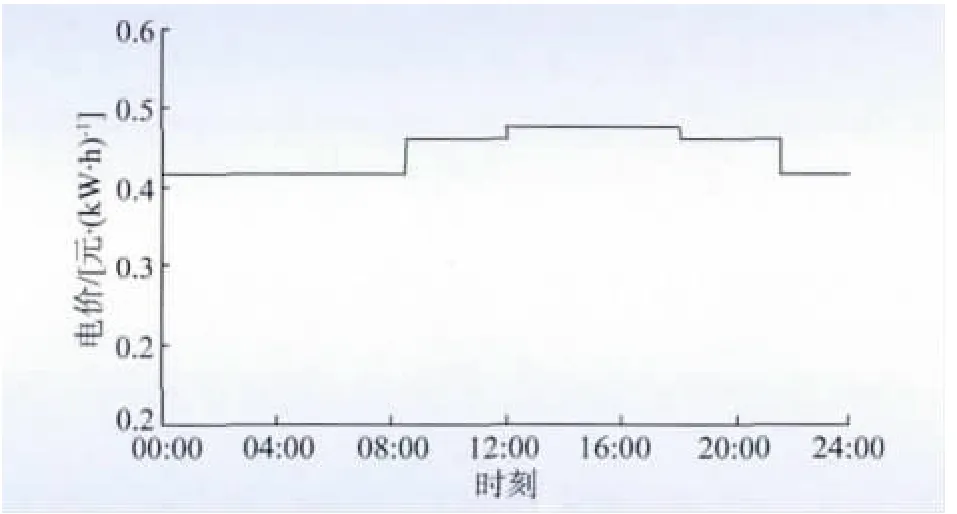
图3 实时电价曲线Fig.3 Spot power price curve

表1 调度时段Table 1 Dispatch interval h

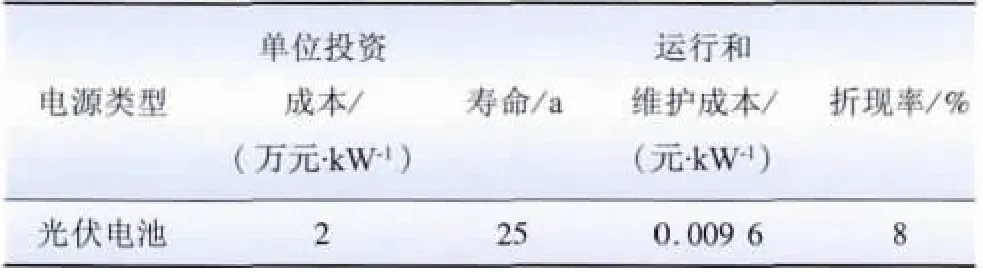
表2 光伏发电系统的设备参数Table 2 Parameters of PV generation system

4.2 结果分析

通过采用第1 节中的综合网损微增率方法进行光伏发电系统的优化布置，如图4 所示，从图4 计算结果可知:节点30 的综合网损微增率dL 绝对值最大节点为0.174 0，其次为节点29 (0.154 6)、节点26(0.159 0)和节点5(0.147 5)，n 表示母线号。可通过比较，在节点30、29、26 和5 装设光伏发电系统，有序地接入，能够更好地提高系统的供电可靠性。

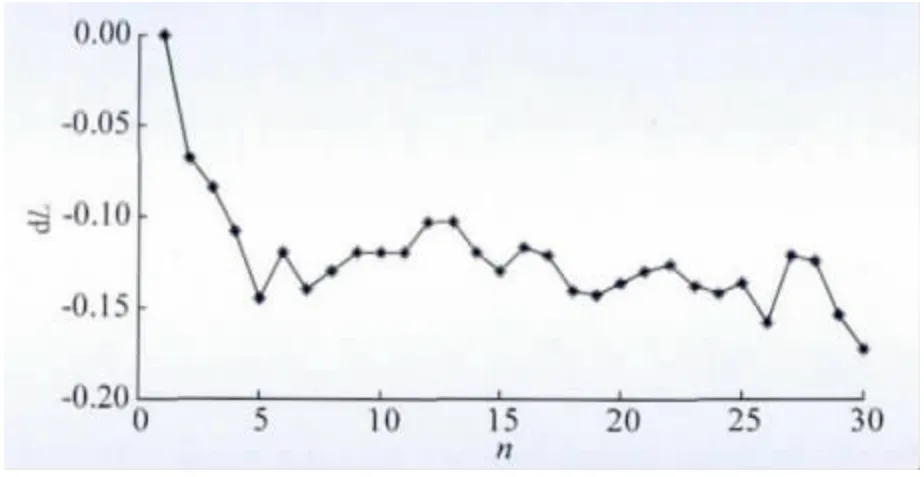
图4 综合网损微增率Fig.4 Comprehensive micro incremental rate

在确认了安装位置后再确定光伏发电系统的容量优化配置。本文考虑了以配电网运营商规划期的经济成本、网损、环境和电压质量4个方面的指标为评价指标构成多目标函数，采用混沌遗传算法进行求解，并通过IEEE －30 系统进行仿真验证，仿真结果表明采用该方法能够实现配网系统的合理优化配置，从而保证城市配网系统的稳定、可靠、安全运行。本文假设只针对1个位置进行光伏发电系统的接入，那么根据综合网损微增率的比较可得，30 节点为光伏发电系统的接入位置，而且假设权重因素都相同，得出如下结果。表3 为发电机污染物的排放量。

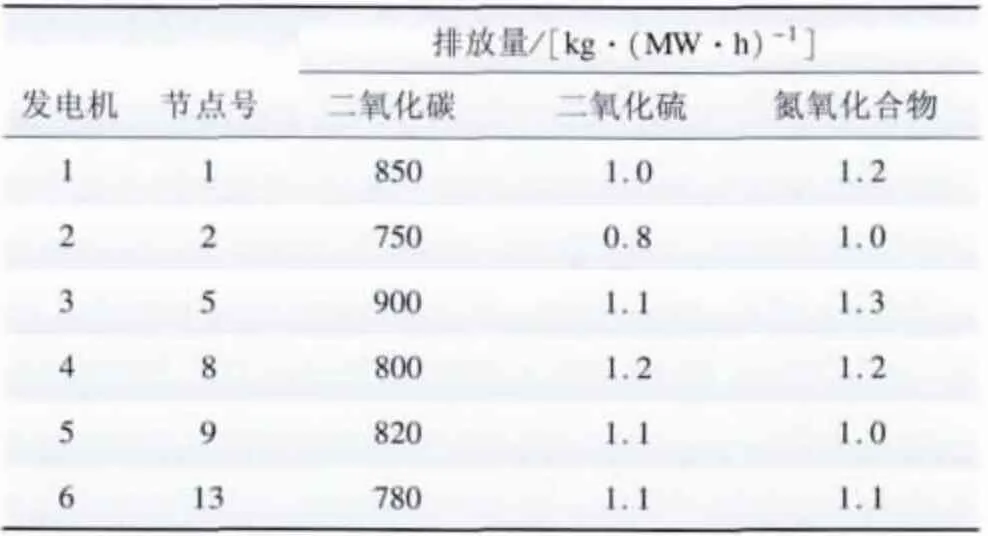
表3 发电机污染物的排放量Table 3 Pollutants mission of generators kg/(MW·h)－1

通过采用带辅助搜索空间的BPSO 算法，得出结果见表4。

表4 运行结果Fig.4 Running results

表4 的运算结果表明，需要在节点30 配置的光伏发电系统的容量为0.455 MW，主要的4个指标分别为经济成本指标为3 436 463元、网损指标为1.190 2、电压质量指标为1.013 7、环境指标为1.190 5，算例结果表明，通过光伏系统的接入有效地降低了系统的网损，提高了系统的环保效益，改善了系统的电压水平，对推进新能源并网发电具有重要的作用。

5 结 论

针对光伏发电系统的选址、定容问题，本文采用有功、无功网损微增率来确定光伏发电系统的接入位置，提出综合微增率，通过计算综合微增率来确保城市配网系统的网损最小。同时提出了一种配电网接入光伏发电系统的多目标规划方法，以配电网运营商规划期的经济成本、网损、环境和电压质量4个方面的指标为评价指标构成多目标的函数，提出带辅助搜索空间的BPSO 算法进行求解，并通过IEEE －30 系统进行仿真验证，仿真结果表明采用该方法能够实现配网系统的合理优化配置，从而保证城市配网系统的稳定、可靠、安全运行。

［1］冉娜．国内外分布式能源系统发展现状研究［J］．经济论坛，2013，10(4):1-6．

［2］郭春菊．分布式电源接入对配电网运行的影响［D］．上海:上海交通大学，2013．

［3］SJEFC． Impact of photo voltaic generation on power quality in urban areas with high PV population［OL］.2013．

［4］Subrata Mukhopadhyay，Bhim Singh． Distributed generation-basic policy，perspective planning，and achievement so far in india［C］//2013 Power ＆Energy Society General Meeting (PES)，Calgary AB，Canada，2012:1-7．

［5］黄少荣．粒子群优化算法综述［J］． 计算机工程与设计，2009，3(30):25-28．

［6］Soroudi A，Ehsan M，Caire R，et al． Possibilistic evaluation of distributed generations impacts on distribution networks［J］． IEEE Transactions on Power Systems，2013，26(4):2293-2301．

［7］Keane A，Ochoa L F，Vittal E，et al． Enhanced utilization of voltage control resources with distributed generation［J］． IEEE Transactions on Power Systems，2011，26(1):252-260．

［8］张文亮，刘壮志，王明俊，等． 智能电网的研究进展及发展趋势［J］．电网技术，2009，33(13):7-11．

［9］常康，薛峰，杨卫东． 中国智能电网基本特征及其技术进展评述［J］．电力系统自动化，2009，33(17):10-15．

［10］刘自发，葛少云，余贻鑫． 一种混合智能算法在配电网络重构中的应用［J］．中国电机工程学报，2010，25(15):73-78．

［11］刘自发，葛少云，余贻鑫． 基于混沌粒子群优化方法的电力系统无功最优潮流［J］．电力系统自动化，2005，29(7):53-57．

［12］Victoire T，Jeyakumar A E． Hybrid PSO – SQP for economic dispatch with valve-point effect［J］． Electric Power Systems Research，2014，71(1):51-59．

［13］Sensarma P S，Rahmani M A． Comprehensive method for optimal expansion planning using particle swarm optimization［C］//Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference．New York，USA，2012:1317-1322．

［14］胡家声，郭创新，曹一家． 一种适合于电力系统机组组合问题的混合粒子群优化算法［J］． 中国电机工程学报，2004，24(4):25-29．

［15］唐剑东，熊信灵，吴耀武，等．基于改进PSO 算法的电力系统无功优化［J］．电力自动化设备，2004，24(7):81-84．

［16］余欣梅，李妍． 基于PSO 考虑谐波影响的补偿电容器优化配置［J］． 中国电机工程学报，2003，23(2):26-30．