含大规模电动汽车的电力系统机组组合问题研究

吴 可，汪 春，孙海顺，张祥文，许晓慧，张 聪

(1．强电磁工程与新技术国家重点实验室(华中科技大学)，武汉市430074;2．中国电力科学研究院，北京市100192)

0 引 言

随着化石能源逐步枯竭、燃料价格不断攀升、全球气候持续变暖所带来的能源危机、环保问题以及新能源的全面开发和利用，电动汽车(electric vehicle，EV)由于其经济和清洁在国际上逐步受到重视［1-3］。当前，美、英、法、日等国已出台了相关政策来推动电动汽车产业的发展，我国也出台了相应的电动汽车国家标准及补贴政策，2014年发改委印发《政府机关及公共机构购买新能源汽车实施方案》，这说明电动汽车是未来汽车工业的发展方向。

大规模EV 接入电网将会对电力系统的规划、运行及市场运营产生很大的影响。一方面，EV 作为电力负荷，它的充电行为具有随机性、间歇性，其充电过程中使用的整流装置在工作时产生的大量谐波会给电网带来谐波污染;另一方面，V2G(vehicle to grid)技术的发展使得EV 可以作为一个个分布式电源，在需要时向电网反馈电能。现有的研究工作表明绝大多数EV 在1 天中96%的时间里是闲置的，从而可以对EV 的充放电进行控制来减小其对电网的不利影响，甚至利用其为电网提供辅助服务［4-5］。

含大规模EV 的电力系统的优化调度是必须要面对和解决的问题［6-7］。对于考虑大规模EV 入网后的机组组合，需要将EV 的充电需求纳入到约束条件中，并对EV 的充电及机组的出力进行协调控制，以使发电成本最小。该问题在国内外已有一些研究成果:文献［8］在目标函数中加入电池电荷状态的罚函数，以保证EV 离网时的SOC 在尽可能不影响机组组合成本的条件下越高越好，但文中没有对EV 的并网时间予以限制;文献［9］以发电机组的运行成本和二氧化碳排放量加权和最小化为目标函数，把每时段内充放电的EV 数量作为可优化调度变量，采用分段线性化方法进行求解;文献［10］建立了考虑入网EV 运用V2G 技术进行反向放电的机组组合模型，使用粒子群算法进行求解，分析表明，利用V2G 技术，EV 可以被看做常规小型发电机组，但该文假设EV 的充电需求都由新能源提供，且没有考虑EV 的充电负荷特性。

本文提出了一种计及电动汽车充电需求的电力系统机组组合模型，以10 机系统为算例，分析了不同EV 规模下，机组启停计划、发电成本及电动汽车充电安排的结果，对比了3 种不同充电控制策略，即无序充电策略、分时电价策略、智能充电策略对电力系统机组最优组合优化结果的影响。

1 电动汽车充电负荷的计算

1.1 电动汽车充电负荷的影响因素

电动汽车规模及类型、充电模式、电池容量、用户出行规律、充电控制策略是影响电动汽车充电负荷的主要因素［11］。

(1)电动汽车规模由电动汽车渗透率，即电动汽车保有量与总汽车保有量的比值来体现。电动汽车类型根据用途可分为私家车、出租车和公交车，根据驱动系统可分为纯电动汽车、插电式混合动力电动汽车及燃料电池电动汽车。

(2)我国电动汽车充电模式根据工业和信息化部于2010年通过的《电动汽车传导式充电接口》，可分为慢速充电、常规充电和快速充电［12］。各种模式额定参数以及典型应用场景如表1 所示。此外，对于公交车和私家车可以采用换电的充电模式，即通过直接更换电池组来达到充电的目的，整个电池更换过程可以在10 min 内完成。

表1 电动汽车充电模式Table 1 Charging modes of electric vehicles

(3)用户的出行规律包含结束行驶时刻、用户离开时刻、行驶里程、期望电量等。

(4)充电控制策略主要分为无序充电、分时电价政策及智能充电。无序充电一般是在最后一次出行结束后或当电池电量低于一定阈值时开始充电，当电动汽车规模较大时，无序充电可能导致电动汽车负荷集中在负荷高峰期充电，对电网产生不利影响。分时电价政策是一种间接调控机制，指在负荷低谷期通过降低电价来引导用户在低谷期充电，起到一定的填谷作用。智能充电则是直接调控机制，通过合理安排电动汽车的充电计划，实现电网的最优运行。

由于公交车、出租车长时间出行在外闲置时间较少，对于电能的需求比较急迫，可调控空间较少，因此本文的研究对象主要为采用慢充方式的私家车。

1.2 电动汽车充电负荷的计算

对于某一台电动汽车，预测其在1 天内的充电负荷分布的关键在于确定其充电功率、充电起始时刻、离网时刻以及充电持续时间。

充电功率PEV主要由充电模式决定，对于慢速充电，充电功率通常在3 kW 附近取值［13］。

充电起始时刻t0取决于EV 的充电控制策略。无序充电控制策略下EV 一旦并网即给其充电，电量达到用户需求或EV 离网时停止充电，因此EV 并入电网时刻即为t0;分时电价控制策略尽可能选择在谷电价时段充电来选择起始充电时间t0;而智能充电控制策略是在满足用户充电需求的前提下，对某一EV 在某一时段是否充电进行安排，对起始充电t0实现智能控制。

在PEV及t0、td确定之后，EV 的电池容量C、起始荷电状态SOC－t0、车主在离网时期望达到的荷电状态SOC-need决定了充电持续时间Tc，即

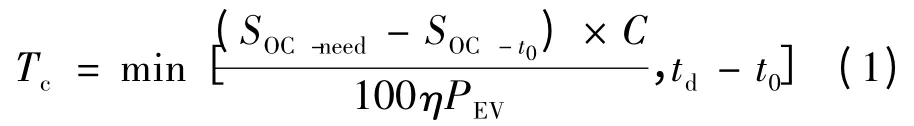
式中:η 为充电效率;故td为EV 离网时刻。式(1)表示实际充电持续时间是在并网时长与为达到用户需求所需充电时长两者中取较小者，即EV 充满电或者EV 离网都将结束充电。

对于某一时刻t 的电动汽车总负荷PtΣEV，将该时刻所有正在充电的EV 负荷进行累加即可得到。

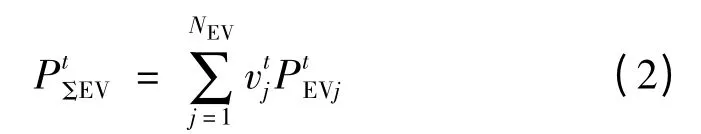
2 含大规模电动汽车的机组组合最优模型及求解策略

2.1 目标函数

在传统机组组合中，由于基本负荷需求一般较为稳定，常由经济性较好但响应速度较慢的大机组来满足，当系统负荷产生波动时，则由响应速度较快但成本较高的小机组来满足。当电动汽车接入电网之后，通过合理安排电动汽车的充电计划达到削峰填谷的作用，可以降低系统对“小而贵”机组的依赖，从而降低机组组合的成本。本文采用与传统机组组合问题相同的目标函数，即机组发电成本最低［14］:式中:为第i 台发电机组第t 时段的出力;为第i台发电机组第t 时段的状态，当其处于运行状态时为1，否则为0;为第i 台发电机组第t 时段连续停机时间;为第i 台发电机组第t 时段的燃料成本函数;为第i 台发电机组第t 时段的启停成本函数;Ng为发电机组总数;T = 24 ，为总优化时段。

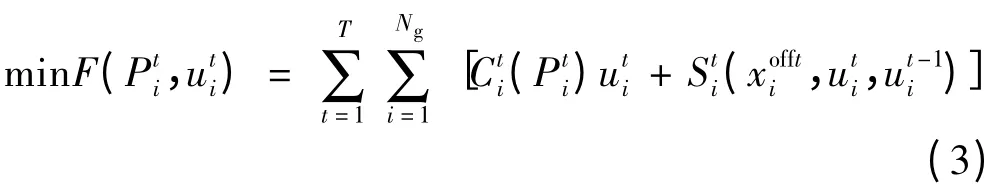
具体的发电机组燃料成本和启停成本分别如式(4)、式(5)所示。

式中ai，bi，ci为第i 台发电机组燃料成本系数。

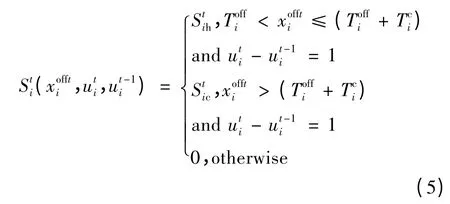
2.2 约束条件

(1)负荷平衡约束。

(3)旋转备用约束。

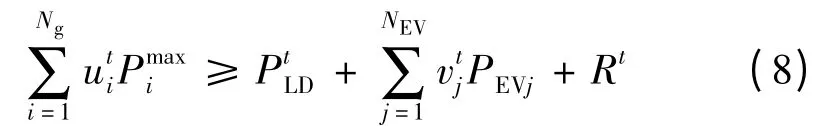
式中Rt为t 时段系统旋转备用容量需求。

(4)发电机组启停时间约束。

发电机状态从开机到停机:

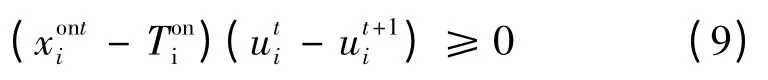
发电机状态从停机到开机:

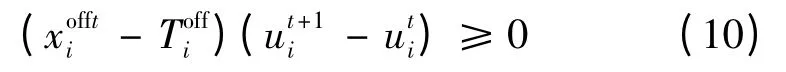
(5)爬坡约束。

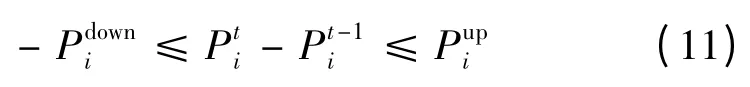
(6)电动汽车用户充电需求约束。

为了满足电动汽车充电需求，需要满足如下蓄电池电量关系:

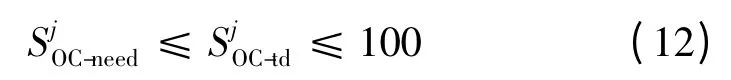
电池各个时刻的电量存在以下递推公式:

(7)充电时间约束。

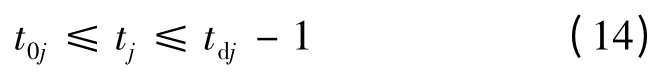
式中:t0j为第j 辆电动汽车开始并网时刻;tdj为第j 辆电动汽车离网时刻，tj为给第j 辆电动汽车充电的时刻。该式对智能充电方案下的电动汽车的充电时间进行了约束，表明只有在电动汽车并网之后、离网之前，才可以根据电网侧和用户侧的双重需求进行调控。

上述式(3)～(14)组成的优化模型为非线性混合整数规划问题。本文采用YALMIP 建模软件在MATLAB 中进行模型的搭建，调用CPLEX 求解器进行计算。为便于求解，对模型的目标函数及约束条件进行部分线性化［15］。

3 算例分析

3.1 算例数据

本文以10 机系统为例，相关系统数据参数详见文献［15］，给定系统旋转备用容量需求Rt为系统容量的10%。对于电动汽车的场景则用蒙特卡洛抽样进行模拟。假设用户最后一次回家之后即并入电网，第1 天离开断开电网。通过对用户出行规律的统计拟合，得到起始充电时刻服从N(19.5，1.2)的正态分布，第2 天离开时刻服从N(7.5，0.5)的正态分布［9］。当电动汽车的电量小于一定值时用户才会选择充电，本文设置起始荷电状态SjOC－t0为服从(20 ～50)的截断正态分布，期望值为40，均方差为12。用户并网时会设定期望荷电状态，本文统一取SjOC-need=100。EV采取慢速充电模式，充电功率PEVj为服从(3 ～4 kW)均匀分布。EV 采用统一型号的电池，电池容量取Cj=60 kW。充电效率取η=100%。

3.2 算例场景

本算例按照3 种充电策略对EV 构建3 种场景，以对比不同控制策略对电动汽车充电负荷的优化效果，并分析不同并网EV 规模对机组组合结果的影响。

场景1:无序充电控制策略。EV 电动汽车一旦并入电网即刻开始充电，直到电池电量符合用户需求或EV 离网时停止充电。

场景2:分时电价控制策略。设定谷电价时段为01:00AM ～07:00AM，假设车主都是理性的，即希望在电价相对便宜的负荷谷值电价时段将所需电量充满，起始充电时刻ts可由式(15)决定，即

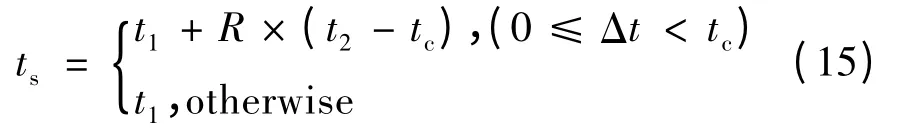
式中:t1，t2为电力部门制定的谷电价区间的起止时刻;Δt = t2－t1，为谷电价区间长度;tc为充电持续时间;R 为［0，1］区间上的一个随机数。

场景3:智能充电控制策略。此时将vtj(第j 辆EV 在第t 时段内是否充电)作为控制变量，以发电成本最低为控制目标对EV 充电安排进行优化。EV 用户充电需求约束及充电时间约束转化为式(16)、(17)，即:

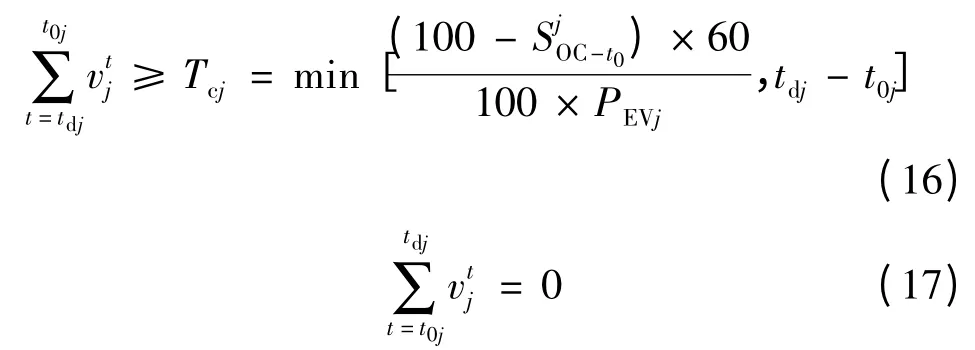
3.3 算例结果

分别设定EV 数量为0，10 000，20 000，40 000辆，在3 种不同控制策略下机组组合优化结果如图1所示。

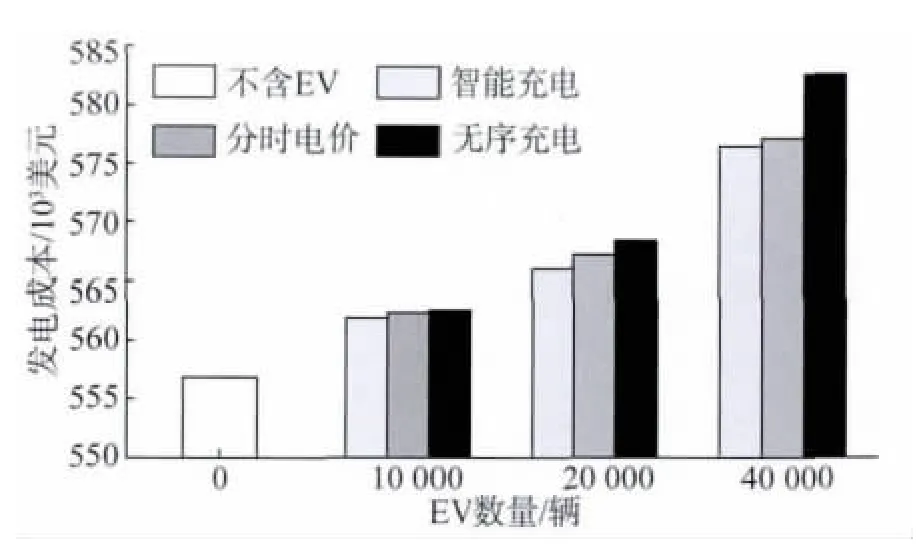
图1 不同EV 规模在3 种控制策略下的机组组合优化结果Fig.1 Optimization results of unit commitment under three EV charging strategies with different scale of EV

从图1 中可以看出，EV 并网会增加发电机组的发电成本，并且发电成本随着EV 规模的增加而不断增大。同时也可以看出，在同一EV 规模下，对EV的充电进行控制能够有效地降低发电成本，且智能充电控制策略比分时电价控制策略具有更为显著的优化效果。

为了进一步讨论不同控制策略对发电成本的优化效果及其原因所在，本文引入了机组经济指标:机组在最大出力下的单位燃料成本［16］，即

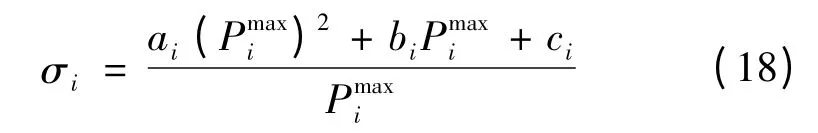
σi值越大，代表机组i 经济性越好。

将机组分为经济型(1 ～5 号机组)和耗费型(6 ～10 号机组)。表2 分别列出了3 种控制策略下的发电总成本、燃料成本、开机成本以及经济型机组和耗费型机组的出力总和。

由表2 中发电总成本、燃料成本及开机成本可以看出:在同一EV 规模下，从无序充电到分时电价再到智能充电，燃料成本均显著减少，且在发电总成本中占有较高的比例，而开机成本的变化趋势并不明显，因此发电总成本也呈现减小的趋势。

由表2 中经济型机组和耗费型机组的出力，可以看出:在同一EV 规模下，从无序充电到分时电价再到智能充电，经济型机组的出力总和与耗费型机组的出力总和变化趋势相反，前者不断增加，而后者不断减小，即系统降低了对“小而贵”机组的依赖，从而降低了机组组合的成本。

为进一步分析不同充电策略对EV 充电计划的优化效果，取EV 规模为40 000 辆，给出3 种充电策略下对某辆EV 的充电安排，如表3 所示。同时对3种充电策略下总负荷曲线进行对比，如图2 所示。

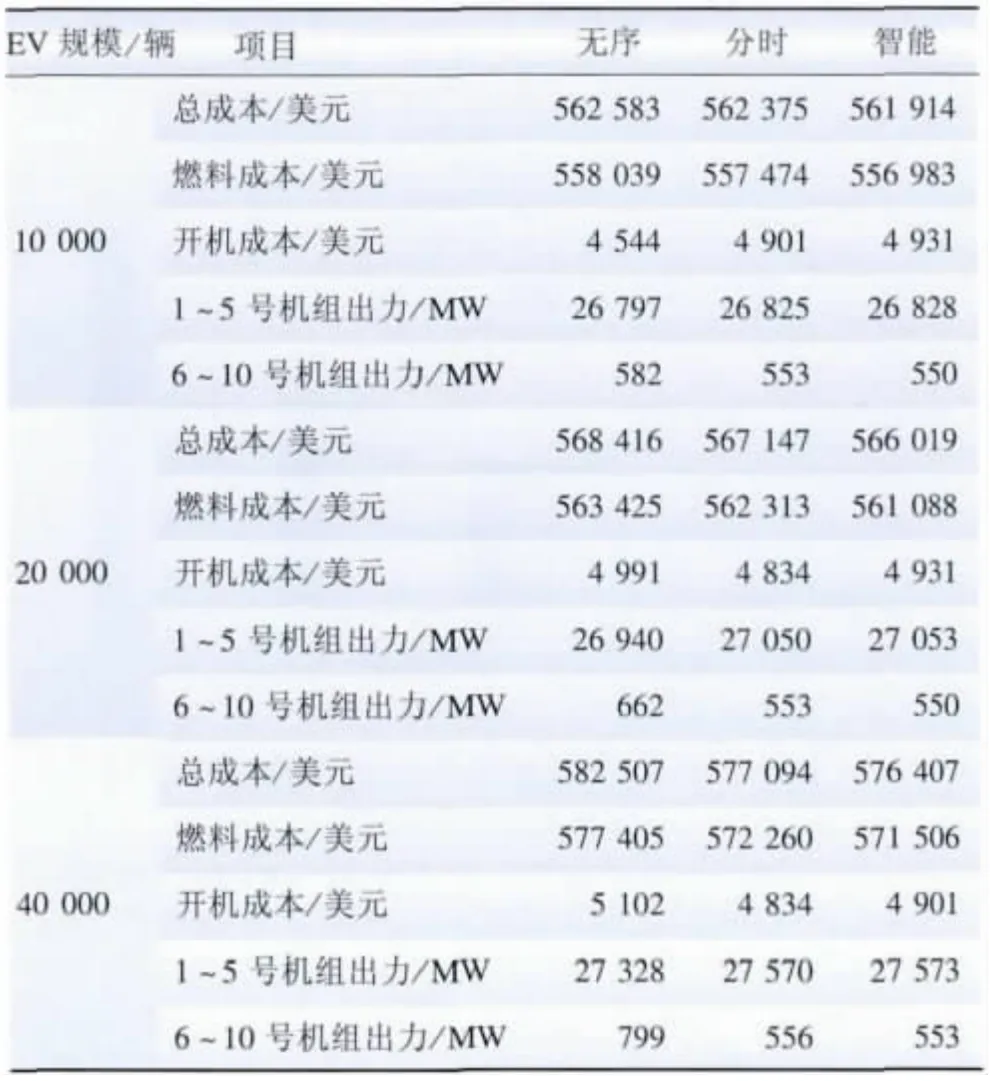
表2 3 种控制策略下各机组燃料、开机成本及出力Table 2 Fuel cost，start-up cost and power outputs of units with three different strategies

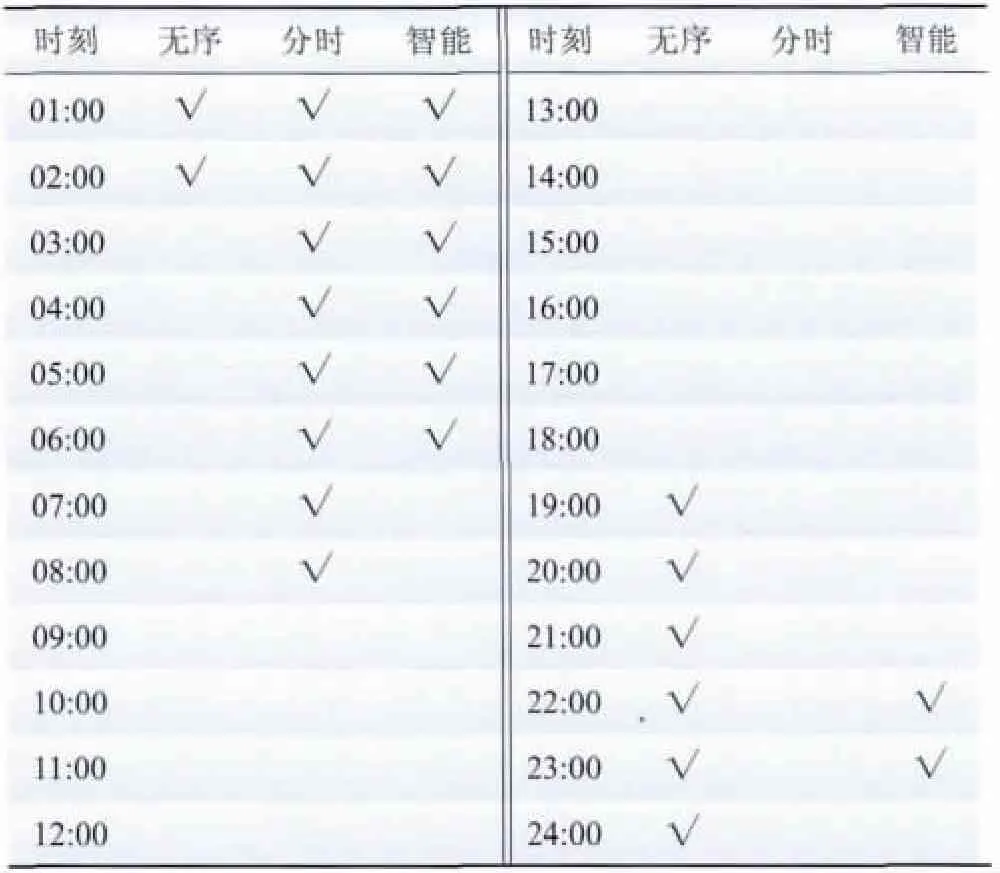
表3 3 种控制策略下某辆EV 的充电安排Table 3 EV charging arrangements under three different control strategies

表3 中对勾符号表示该辆EV 在该时段进行充电，该辆EV 并网时刻为19 时，离网时刻为第2 天7时。从表3 中可以看出，无序充电策略下该辆EV 即插即充，分时电价策略将该辆EV 起始充电时刻从19时转移到了24 时，且该辆EV 是连续充电状态，而智能充电策略下EV 并入电网后并没有立即充电，而是避开负荷尖峰后才开始充电，且非连续充电。

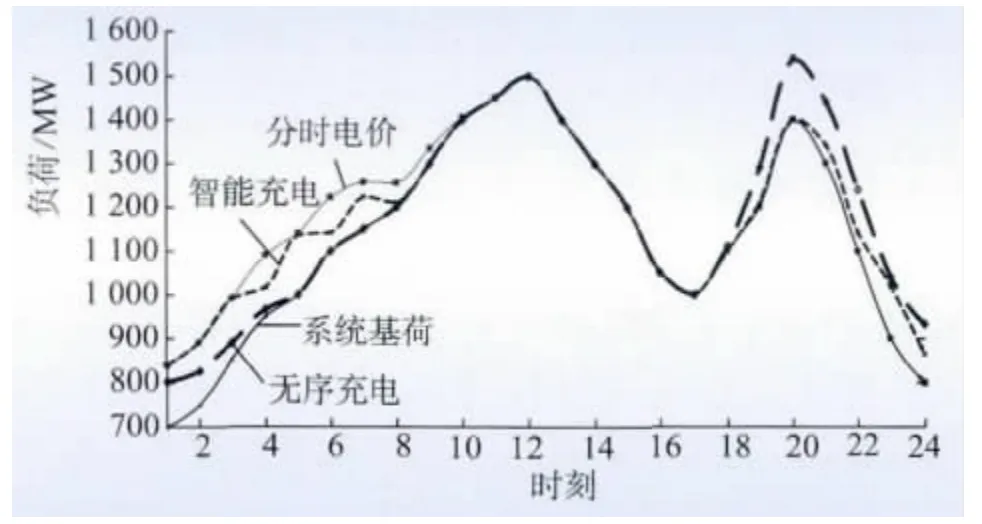
图2 3 种充电策略下系统总负荷曲线Fig.2 System total load curves under three different charging strategies

从图2 中可以看出，从无序充电到分时电价再到智能充电，电网总负荷曲线越来越平整，EV 被大量转移到负荷低谷期进行充电，具有明显的削峰填谷作用。负荷曲线越平滑，则各时段机组出力的调整更灵活，系统可通过增加经济型机组出力、减少耗费型机组出力的方式来降低发电成本。

4 结 论

(1)大规模EV 并网会增加系统发电成本，但是通过对EV 的控制可以实现对机组组合的优化。从无序充电到分时电价再到智能充电，经济型机组的出力总和不断增加，而耗费型机组的出力总和不断减少，因而降低了机组组合的成本。

(2)对EV 采取适当的充电控制策略可以使其将充电时段安排在负荷低谷期，从而发挥其削峰填谷的作用，使系统总负荷更稳定。智能充电策略比分时电价策略对EV 充电安排的优化效果更显著。

［1］Garcia-Valle R，Lopes J A P．Electric vehicle integration into modern power networks［M］．Berlin:Springer，2013．

［2］Wirasingha S G，Emadi A． Classification and review of control strategies for plug-in hybrid electric vehicles［J］．IEEE Transactions on Vehicular Technology，2011，60(1):111-122．

［3］Turker H，Bacha S，Chatroux D． Impact of plug-in hybrid electric vehicles (phevs)on the french electric grid［C］//Innovative Smart Grid Technologies Conference Europe (ISGT Europe)．IEEE，2010:1-8．

［4］高赐威，张亮．电动汽车充电对电网影响的综述［J］． 电网技术，2011，35(2):127-131．

［5］王锡凡，邵成成，王秀丽，等． 电动汽车充电负荷与调度控制策略综述［J］．中国电机工程学报，2013，33(1):1-10．

［6］Saber A Y，Venayagamoorthy G K． Unit commitment with vehicleto-grid using particle swarm optimization［C］// PowerTech，2009 IEEE Bucharest．IEEE，2009:1-8．

［7］Khodayar M E，Wu L，Shahidehpour M． Hourly coordination of electric vehicle operation and volatile wind power generation in SCUC［J］． IEEE Transactions on Smart Grid，2012，3 (3):1271-1279．

［8］赵俊华，文福拴，薛禹胜，等． 计及电动汽车和风电出力不确定性的随机经济调度［J］．电力系统自动化，2011，34(20):22-29．

［9］陆凌蓉，文福拴，薛禹胜，等． 计及可入网电动汽车的电力系统机组最优组合［J］．电力系统自动化，2011，35(21):16-20．

［10］Gaing Z L． Discrete particle swarm optimization algorithm for unit commitment［C］//Power Engineering Society General Meeting．IEEE，2003．

［11］罗卓伟，胡泽春，宋永华，等．电动汽车充电负荷计算方法［J］．电力系统自动化，2011，35(14):36-42．

［12］田亭立，史双龙，贾卓．电动汽车充电功率需求的统计学建模方法［J］．电网技术，2010，34(11):126-130

［13］Garcia-Valle R，Lopes J A P． Electric vehicle integration into modern power networks［M］．Berlin:Springer，2013．

［14］薛松，袁越，傅质馨，等．考虑电动汽车入网技术的电力系统机组组合研究［J］．电力系统保护与控制，2013，41(10):86-92．

［15］Carrión M，Arroyo J M． A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem［J］．IEEE Transactions on Power Systems，2006，21(3):1371-1378．

［16］李高望，钱斌，石东源，等．含插电式混合动力汽车的机组组合问题［J］．电网技术，2013，37(1):32-38．