含风电的电力系统机组组合问题研究综述

刘吉臻，王海东，李明扬

(新能源电力系统国家重点实验室(华北电力大学)，北京市102206)

0 引 言

近年来，能源危机和环境问题愈来愈成为世界各国经济与社会可持续发展面临的严峻问题，我国能源和环境问题更为严重，因此，调整能源结构、积极发展清洁新能源已成为应对能源环境问题最积极、有效的选择。风电作为一种取之不尽、用之不竭的清洁能源，在世界各国得到了迅速发展。然而，风电呈现出了随机性、间歇性的特点，目前风电出力的预测水平还不能满足电力系统实际运行的需要。以风电为代表的新能源规模化开发、利用使电力系统的结构形态、运行特性与控制方式产生了根本性变革，形成了新一代新能源电力系统［1］，这对电网的运行调度水平也提出了新的要求。

电力系统机组组合(unit commitment，UC)是指在满足系统负荷需求、旋转备用和发电机运行技术要求等约束条件的前提下，在1个调度周期内(通常为24 h)合理安排各发电机组的启停和各个时段中机组的出力，从而使整个系统的总发电费用最小。传统的机组组合问题主要涉及常规火力发电机组。

随着风电的大规模接入电网，负荷波动和机组停运不再是影响电力系统稳定的主要因素，传统的机组组合方法已难以应对风电随机性给电力系统带来的影响。含风电的机组组合问题是近年来随风电规模化并网而出现的新问题，主要针对含常规火力发电机组和风电的电力系统。新能源电力系统的机组组合能够在电力系统短期运行中实现各类发电资源的结构性优化，为实时调度预留足够的优化空间，以应对新能源发电的随机性和未来负荷的不确定性，满足系统负荷需求和备用要求，同时，最大限度地平衡系统的经济性和节能性［2］。同时，研究含风电电力系统机组组合方式对于今后大规模接纳太阳能等其他新能源发电也具有重要借鉴意义。

本文分析风电接入系统后对电网机组组合问题带来的影响，分类阐述近年来在求解含风电的机组组合问题时主要的建模方法和常用求解算法，总结当前该问题的研究热点，并对该领域未来的研究和发展进行展望。

1 风电不确定性对机组组合的影响

1.1 风电的不确定性分析

风功率预测是应对风电随机性、波动性对电力系统稳定性和经济性带来影响的，技术手段之一，常见的风电预测技术包括物理方法和统计方法［3］。风电功率日前预测的准确程度会对机组组合的优化结果产生显著影响，然而全球范围内实际投入商业运行的风电预测软件的平均绝对百分误差(mean absolute percentage error，MAPE)约为14% ～20%［4］。因此，在现有技术条件下，单纯依靠风功率的预测无法解决风电随机性对机组组合带来的影响。

传统电力系统在进行机组组合时，主要考虑负荷波动和事故停机带来的波动，而现有的风电功率预测精度使得风电的随机性成为了新能源电力系统机组组合要考虑的主要波动。

1.2 风电并网对系统备用的影响

电网预留一定的发电备用容量，是电网安全、稳定运行的基础，能保证系统在受到一定范围的扰动时，平稳地过渡到新的稳定运行状态［5］。为保证风电并网后电力系统运行的可靠性，增加额外的旋转备用成为了应对风电随机性、保证系统稳定的解决办法之一，但是这种方法本身牺牲了系统运行的经济性，而且，系统中火电机组可能没有足够的爬坡能力提供额外的备用容量，这就使得优化结果脱离了实际。因此，如何准确计算旋转备用容量以应对风电出力和负荷波动、保证系统安全成为了涉及系统旋转备用问题的主要研究难点，主要研究思路分为2 类:

(1)机组组合的滚动制定方法。风电功率预测误差具有随着时间尺度的缩短而逐渐减小的特性，因此机组组合的滚动制定方法可以有效降低风电功率预测误差对机组组合结果的影响。文献［6］将机组组合的周期从原来的24 h 缩短至1 ～24 h 某个值，通过滚动制定的方式不断将最新的信息应用到机组组合中，不断降低系统旋转备用需求，从而得到经济性更好的机组组合结果。文献［7］的思路与此类似，同时在模型中将应对风电不确定性而增加的旋转备用作为小概率备用需求，模型将系统运行的经济性和安全可靠性分散到不同时间尺度的机组组合中分别侧重考虑，通过各级机组组合的协调优化，降低了系统的发电成本。

(2)兼顾可靠性和经济性的方法。通过增加额外的旋转备用应对风电随机性的方法在提高系统可靠性的同时也降低了系统的经济性，寻找系统可靠性和经济性的平衡点是确定系统旋转备用关键。文献［5］建立了考虑风电对系统经济性和环保性综合影响以及风电提供备用可能性的机组组合模型;文献［8］基于成本效益分析方法，研究了综合考虑系统可靠性和经济性及机组的强迫停运率、负荷和风电出力预测偏差等不确定性因素时，系统最优旋转备用容量的确定方法;文献［9］通过增加负荷跟踪时间约束和快速旋转备用约束，建立了兼顾系统运行效益和备用效益的机组组合模型。

1.3 风电并网对电网安全的影响

强随机性的风电大规模接入电网在带来环保效益的同时，也给电力系统的安全、稳定运行带来了新的挑战。考虑安全约束的机组组合(securityconstrained unit commitment，SCUC)作为常规机组组合问题的扩展，主要在常规机组组合问题上考虑网络安全约束，包括节点电压约束和线路潮流约束［10］。对于含风电的电力系统，考虑安全约束的机组组合显得尤为重要。现有的相关研究主要分为2 类:

(1)大部分学者主要是在常规方法的基础上引入了广义网络安全约束，从而降低风电随机性对电网安全带来的影响。例如，文献［11］提出的机组组合模型在通过场景法处理风电随机性的同时，考虑了广义网络安全约束和场景的网络安全约束;文献［12］在建立含风电和空气压缩储能系统的安全约束机组组合模型时，考虑了线路潮流限制和节电电压限制;文献［13］在求解含风电场的安全约束机组组合模型时，通过引入发电机功率因子，简化了线路容量约束的表达。

(2)也有部分学者考虑到风电机组具有无功调节功能，文献［14］提出的安全约束机组组合方法考虑了风电机组无功特性，该方法将风电出力作为1个区间放入传统机组组合模型，用于处理风电的波动性;采用交流潮流约束，也避免了大量异步风电机组存在而导致的相关节点无功不足且电压越限的问题。

1.4 风电并网对电网结构的影响

近年来，储能技术得到了飞速发展，将储能系统引入含风电的电力系统，形成“传统发电——新能源发电——储能系统”一体化的新能源电力系统，储能装置的引入可以从一定程度上提高系统运行的灵活性，降低风电随机性对系统的不利影响［15］，这为解决含风电的机组组合问题提供了新的方向。文献［16］从储能系统的有无变化、储能系统不同容量变化等角度分析了储能系统对机组组合问题的影响;文献［12］建立了含风电场和空气压缩储能系统的安全约束机组组合模型;文献［17］针对含储能装置的电力系统，建立了基于极限场景集的日期机组组合模型，并证明了储能系统可以平抑风电波动，使系统可以接纳更多风电。

2 建模方法

2.1 概述

风电并网对机组组合问题的影响主要在于如何处理随机性的风电出力，降低其不确定性对机组组合结果的影响。因此，现有学者在进行相关建模时的研究点主要集中在风电随机性处理方法的差异上。按照对风电随机性处理思路的不同，含风电机组组合问题的常见建模方法主要分为模糊建模、机会约束规划建模、场景法建模。

2.2 模糊建模

模糊建模的基本思路是将不确定的风电出力看作是模糊数，通过隶属度函数来模糊处理风电场出力，建立风电场出力隶属度函数μWS(k)，该值越大表明决策者对于风电场出力的满意度越高。同时，建立各目标函数和约束条件的隶属度函数，包括总费用隶属度函数μTC(k)、负荷平衡隶属度函数μLD(k)、旋转备用隶属度函数μSR(k)。然后根据模糊集理论的最大最小法则，定义全局隶属度作为整个模型的模糊满意度指标

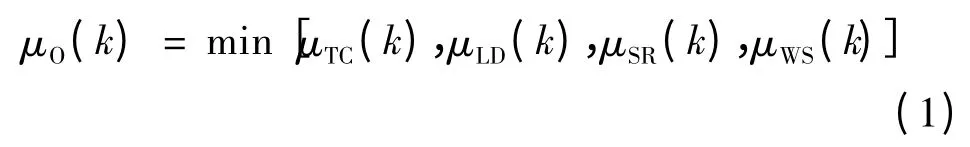
这样，模型求解问题就转化为了满足约束条件的满意度指标μO(k)最大的问题。μO(k)的值反映了决策者对整个机组组合结果的全局满意度，包括总发电费用、负荷平衡情况和旋转备用情况。当μO(k)取值接近或等于1 时，表明机组组合结果满足决策者的要求。

不同学者在采用模糊理论处理风电随机性时的思路类似，主要区别在于所建立的局部隶属度函数和全局隶属度函数有所差异。

(1)一种思路是直接建立风电出力大小的隶属度函数，例如，文献［18］和文献［19］的建模方法类似，先建立了风电场有功出力隶属函数和总耗量成本隶属度函数，然后取这2个隶属度函数中对应的最小值作为满意度指标，解决了含风电场机组组合问题中风电场输出功率难以准确预测带来的不确定性。

(2)文献［20－22］则没有直接建立风电出力大小的隶属度函数:文献［20］建立了风速误差隶属度函数，其本质还是反映了风电出力大小是否满足决策者的预期值;文献［21］则通过建立弃风电量的隶属度函数来反映决策者对风电实际出力的满意度;文献［22］采用电量不足期望值来量化风电不确定性带来的影响。

模糊建模方法解决了风电出力不确定性对电力系统机组组合带来的问题，决策者对于风电出力的意愿可以在机组组合结果中得到充分体现;同时，该方法可以将多目标优化问题转化为了单目标优化问题，降低了问题求解难度，粒子群优化算法［18，20］、遗传算法［19］和混合整数规划法［22］均可完成模型求解，模型思路清晰、简易。但是，在这种建模方法中，隶属度函数的确定直接影响到模糊建模结果的好坏。而隶属度函数所涉及建模对象的理想值及函数形状通常是根据试验或者经验来确定，并没有一套相对客观、规范的确定方法，因此模型本身的精度无法验证。

2.3 机会约束规划建模

2.3.1 随机机会约束规划

在机组组合问题中，由于风电的不确定性，将约束条件确定性处理后势必会使得计算结果偏于保守。随机机会约束规划是随机规划的重要分支，主要针对约束条件中有随机变量，且必须在观测到随机变量的实现之前做出决策的优化问题［23］。考虑到所作决策在不利的情况发生时可能不满足约束条件，允许所作决策在一定程度上不满足约束条件，但是，该决策应该使约束条件成立的概率不小于某一置信水平。机会约束规划的一般形式为式中:f(x)为目标函数;x 为决策向量;ξ 为参数向量;g(x，ξ)≤0 为约束事件;α 为置信水平;Pr{·}表示事件成立的概率。

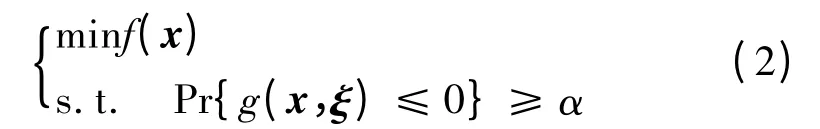
该种建模方法的基本思路是将风电出力看作服从某种概率分布的随机变量，用机会约束规划条件替代包含该随机变量的约束条件。国内外学者在采用机会约束规划对含风电机组组合问题建模时，所采用的通过机会约束处理风电随机性的方式有所不同，通常可以分为2 种思路。

(1)通过将风电的随机性影响作为机会约束条件，在满足随机性影响的前提下最大限度地利用风电，文献［24－27］均采用了这种思路:文献［24］分别从24 h 风力发电总量、单位小时内风电的利用率和运行时单位小时内风电利用率提出了3 种机会约束条件，保证了每个时段内绝大部分的风力输出都能得到有效利用;文献［25］引入风电可信度指标来处理风电的随机性，模型在风电可信度指标下实现风能的最大化利用;文献［26］主要考虑了市场价格变动和风电出力波动2个不确定因素，采用机会约束最大程度提高风电利用率;文献［27］引入了机会约束来限制电力不足期望值和弃风量期望值。

(2)将机组出力等条件作为机会约束条件，尽可能地降低风电随机性的影响，文献［28］引入机会约束规划来处理负荷波动、火电机组故障停运、能源价格变动和新能源发电出力波动等随机因素，使机组总的出力满足负荷需求的概率不小于某一置信水平，以保证电网负荷平衡。

机会约束规划建模可以定量地描述风电出力的概率分布特性，有效解决了风电出力随机性对电网机组组合带来的问题;同时，机会约束的概念能描述系统的置信水平，决策方案能够兼顾不确定环境下的风险与成本。

在求解机会约束规划时，传统的思路是将机会约束转化为其确定等价类，然后求解其等价的确定性模型即可。然而，这种方法仅仅限于一些特殊情况，在大部分情况是无法完成这一转化的。因此，模型的求解成为了机会约束规划的难点。文献［24－28］在进行模型求解时均借助了其他算法，例如抽样平均逼近法、线性混合整数规划法、粒子群算法等，但求解过程均偏繁琐。

2.3.2 模糊机会约束规划

模糊机会约束规划主要针对机会约束规划中决策环境存在模糊参数的情况［23］，模糊机会约束规划的建模思想与随机机会约束规划类似，即允许所决策结果在一定程度上不满足约束条件，但该结果使模糊约束条件成立的可能性不小于预先给定的置信水平［29］。

文献［30］将风电出力的模糊性转化为预测误差的模糊性，基于可信性理论推导了风电预测误差的可信性分布函数，并据此建立了旋转备用的模糊机会约束条件，进一步得到了机组组合的模糊机会约束模型;文献［31］首先引入模糊理论，将间歇式电源出力和负荷用模糊参数表示，把传统机组组合模型的确定性的系统约束改为模糊参数下的系统约束，并基于可信性理论形成了模糊机会约束，建立了含多模糊参数的模糊机会约束机组组合数学模型。

2.4 基于场景法的建模方法

2.4.1 随机场景法建模

场景法是解决随机过程问题的重要工具。图1是一个典型的场景树，其中每个结点代表随机过程的1个决策点，每个树的分支代表1个随机决策结果。Heitsch H 和Römisch W 等在场景树的证明和使用方法上做了较多的研究，他们在文献［32］中详细论述了场景树法在多级随机过程中的应用;在文献［33］中详细论述了场景树的生成、缩减和重构方法。

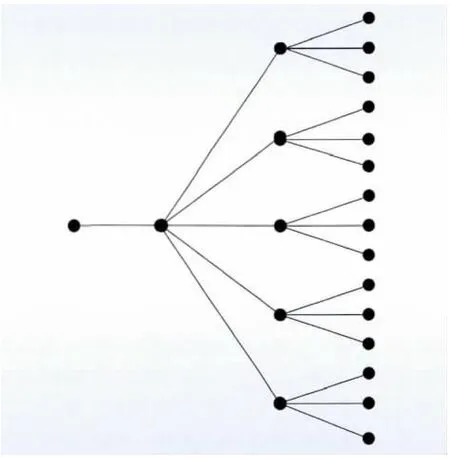
图1 典型场景树Fig.1 A typical scenario tree

采用场景法解决含风电机组组合问题的基本思路是根据风电概率分布抽样生成大量场景，对各个场景分别求解，最终将不同场景下的发电费用的加权平均值，即期望发电费用作为决策结果［34］。场景法主要分为3个步骤:场景产生、场景缩减和场景树构建。文献［35］给出了一种生成有限场景的方法并证明了方法的正确性。

由于场景的数量会随着时间段的增加呈指数形式增长，使计算难度大大增加;场景缩减虽然可以降低计算的难度，但同时也会影响了计算的精度。因此，如何在保证一定精度的前提下进行场景缩减成为了使用场景法的关键。

(1)在进行场景缩减时，比较传统的方法是基于概率距离来进行缩减。文献［36］提出了采用概率距离进行场景缩减的基本思路，即使得缩减后的场景集合与缩减前的场景集合之间的概率距离最小，从而将场景缩减对计算精度的影响降到最低程度;文献［37］使用Kantorovich 距离来描述这一概率距离;文献［38］将这一场景缩减方法应用到了含风电的机组组合问题中，模型中采用场景树方式描述日前风电场输出功率的时间分布特性，在保证较高计算精度的前提下，利用场景缩减技术降低了模型复杂度;文献［39］在使用场景法分析含风电机组组合中旋转备用的确定时采用了这一场景缩减方法;文献［40］将场景法和机会约束规划结合来建立含风电场的机组组合模型，在借助场景法完成了对风电不确定性的建模时采用了同样的场景缩减方法。

(2)也有一些学者通过其他方法完成了场景缩减。文献［13］通过引入发电机功率分布因子来取代场景缩减方法，使模型在计算时间和计算精度方面均得到了改善;文献［41］采用正态分布描述风电出力的预测误差分布，通过离散化处理确定系统的各个场景;文献［42］在求解同时含风电、火电、核电和抽水蓄能电站的机组组合问题时，采用场景法处理来自负荷和风电出力的波动性，提出了一种基于粒子群优化算法的场景缩减方法并证明了方法的可行性。

场景树法将含风电机组组合问题求解过程中风电的不确定性处理转化为多个场景下的确定性计算，能够在一定程度上适应风电的随机性。然而，原始场景树因场景规模过大无法求解，各种场景缩减方法虽然降低了计算量，但由于不能涵盖所有场景，模型精度下降，决策结果的风险无法量化。模型的计算效率和计算精度之间的矛盾是该模型关键问题所在。

2.4.2 鲁棒机组组合

鲁棒优化是一种解决系统中出现不确定性扰动的数学规划方法［43］，不确定性参数通常出现在约束条件中，也可出现在目标函数。在含风电的机组组合问题中，不确定性因素出现在约束条件。基于场景法进行的含风电机组组合建模的另一种思路就是基于最坏场景集下的鲁棒优化，即保证不确定性环境下系统的安全、可靠运行，降低系统的运行风险［44］。

含风电的鲁棒机组组合模型主要要求模型能在对未来目标时段电力系统运行信息掌握不完全的情况下，对不确定性因素有一定免疫能力，能够在一定扰动范围内保证电力系统安全、稳定运行，并尽量实现机组组合的目标［45］。单纯的鲁棒机组组合结果往往比较保守，一定程度上牺牲了经济性，因此，将抗风险鲁棒性和发电成本共同优化更具有实际意义［46］。

文献［47］提出了一种基于坏场景集的鲁棒机组组合模型，通常将误差最大情况下的场景定义为坏场景集，定义坏场景集鲁棒性度量为

式中:u 表示机组组合状态;ωs为场景s 发生概率;f(u，s)表示场景s 下可行解u 对应的发电成本;EC(u)为各场景集下成本的期望值;VC(u)表征的是可行解u 在总的坏场景集S 下的成本方差。

模型的目标函数为

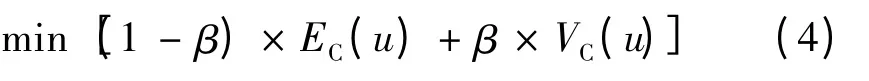
式中β∈［0，1］为平衡目标函数中成本与方差权重的因子。这一模型在平抑风电不确定性带来的影响的同时，保证了系统的经济性。由于鲁棒决策结果很大程度上取决于场景集的选择，因此坏场景集的选择直接影响到优化结果。

3 求解算法

3.1 概述

传统的机组组合问题已经有很多成熟的求解算法，包括:经典算法，如启发式方法;数学优化方法，如动态规划法、混合整数规划法、拉格朗日松弛法等;智能优化算法，如粒子群优化算法、遗传算法等。风电的随机性使得这些传统的方法不能直接用于含风电机组组合问题的求解。近年来，国内外学者在这些方法的基础上进行了不同程度的改进，以适应含风电的机组组合问题的求解，本文主要介绍以下几种常用算法。

3.2 常用算法介绍

3.2.1 混合整数规划法

混合整数规划(mixed integer programming，MIP)是变量中既包含整数又包含非整数的数学规划问题，根据除整数变量以外的其他变量的函数类型，又可分为线性混合整数规划和非线性混合整数规划［48］。在传统的机组组合问题中，混合整数规划法已经有了广泛的应用［49］。

然而，随着大规模风电接入电网，风电的随机性问题使得传统的混合整数规划法在求解含风电场的机组组合时陷入了计算时间过长的问题。国内、外学者在使用混合整数规划时，均进行了不同的改进或与其他方法进行结合。文献［13］通过引入功率分布因子，降低了MIP 求解安全约束机组组合问题的求解时间;文献［16］将含风电和储能系统的机组组合问题描述为混合整数凸规划形式，并采用分支定界－内点法进行求解;文献［30］在建立含风电的机组组合模糊机会约束模型的基础上，结合混合整数线性规划完成了模型求解。

3.2.2 拉格朗日松弛法

拉格朗日松弛法(Lagrangian relaxation，LR)的基本原理是利用松弛因子把各种约束条件写入目标函数从而消去约束条件，将约束规划变为无约束规划。拉格朗日松弛法属于传统机组组合问题的经典求解算法之一，文献［50］总结了拉格朗日松弛法在传统机组组合问题中的应用，文献［51］提出了一种求解机组组合问题的改进拉格朗日松弛算法。

拉格朗日松弛法同样适用于含风电的机组组合问题求解。文献［52］采用改进拉格朗日松弛法对机组组合模型进行求解，分析比较了不同备用配置方案的可靠性。

3.2.3 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)起源于对鸟群捕食行为的研究［53］，属于进化算法的一种，其基本思路是从随机解出发，选择合适的适应度来评价解的品质，通过迭代寻找最优解。这种算法以其实现容易、精度高、收敛快等优点，近年来在含风电的机组组合问题求解中得到了广泛应用。

国内外学者在使用PSO 算法求解含风电的机组组合问题时通常进行了不同程度的改进。熊虎等在文献［31］中提出了一种改进的二进制粒子群优化算法，完成了模糊机会约束机组组合模型的求解;文献［40］采用离散粒子群算法求解基于场景树和机会约束规划的含风电的机组组合模型;文献［54］提出了一种基于随机模拟的粒子群优化算法，完成了含风电场的机组组合问题求解。

也有学者将PSO 算法和其他算法结合起来求解含风电的机组组合问题。文献［21］利用粒子群算法和模糊多目标方法完成了含风电的机组组合问题求解;文献［55］将遗传算法和改进的粒子群算法相结合，用于求解同时包含风电、火电以及太阳能发电的机组组合问题。

3.2.4 遗传算法

遗传算法起源于对生物系统所进行的计算机模拟研究，是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法，在函数优化、组合优化、生产调度问题、自动控制等领域发挥着重要作用。遗传算法在执行过程中通常包括个体编码、初始群体产生、适应度计算、选择复制、交叉运算、变异运算几个步骤。传统的机组组合问题中，遗传算法已经得到了广泛应用。文献［56］提出了一种浮点数编码的遗传算法用于求解机组组合问题，文献［57］提出了基于矩阵实数编码的遗传算法来求解大规模机组组合问题，文献［58］采用遗传算法完成了安全约束的机组组合问题求解。在含风电的机组组合问题中，遗传算法通常与其他建模方法结合起来使用，文献［19］在模糊建模的基础上采用遗传算法完成了模型求解。

4 总结与展望

含风电的机组组合问题是近年来随风电规模化利用出现的新问题，虽然国内、外学者为解决这一问题已经从不同角度进行了一系列的研究，但目前还未形成一套相对完整的理论体系和工程方法;而机组组合是消纳大规模并网风电必须解决的重要问题之一，因此，该问题在今后依然是研究热点。本文从并网风电对机组组合的影响、常见建模方法、典型求解算法几个方面总结了该问题现有的研究成果。在今后，需要从以下几个方面入手探究解决该问题的方法:

(1)提高风功率预测的精度。现有的风功率预测的误差太大是含风电机组组合问题难以解决的根源，因此提高风功率预测的精度将是解决这一问题的重要途径之一。

(2)建模方法的优化。从近年来已有成果来看，针对该问题的建模方法主要围绕在模糊建模、机会约束规划建模和场景法建模，这些建模方法或者在能否准确描述问题本身上有待商榷，或者求解过程繁琐。建模是该问题的核心环节，今后应在建模方法上作进一步研究，使该方法既能很好地适应风电随机性的特征、又能平衡好所建模型的精度和计算难度。

(3)研究源－网－荷一体化机组组合模式。规模化利用风电的关键是在随机波动的负荷需求和随机波动的电源之间实现电能的供需平衡，传统的机组组合模式主要通过电网调节电源的出力，从而适应负荷的变化需求。随着智能电网建设的不断深入，负荷需求侧有序参与电网互动运行，协同消纳波动的新能源发电，形成源－网－荷一体化机组组合模式，可以实现能源资源综合利用，为实时调度预留足够的优化空间，以应对新能源发电的随机性和未来负荷的不确定性，最大限度提升新能源电力系统的运行品质。

［1］刘吉臻.大规模新能源电力安全高效利用基础问题［J］.中国电机工程学报，2013，33(16):1－8.

［2］夏清，钟海旺，康重庆.安全约束机组组合理论与应用的发展和展望［J］.中国电机工程学报，2013，33(16):94－103.

［3］丁华杰，宋永华，胡泽春，等. 基于风电场功率特性的日前风电预测误差概率分布研究［J］. 中国电机工程学报，2013，33(34):136－144.

［4］Monteiro C，Bessa R，Miranda V，et al. Wind power forecasting:State－of－the－art 2009 ［R］. Argonne National Laboratory(ANL)，2009.

［5］王彩霞，乔颖，鲁宗相.考虑风电效益的风火互济系统旋转备用确定方式［J］.电力系统自动化，2012，36(4):16－21.

［6］Tuohy A，Denny E，O'Malley M. Rolling unit commitment for systems with significant installed wind capacity［C］//Power Tech，2007 IEEE Lausanne. Lausanne，Switzerland:IEEE，2007:1380－1385.

［7］张娜，吕泉，张显，等.含风电系统的多级机组组合协调制定策略［J］.电力系统自动化，2013，37(11):39－45.

［8］苏鹏，刘天琪，李兴源.含风电的系统最优旋转备用的确定［J］.电网技术，2010，34(12):158－162.

［9］李茜，刘天琪，王福军，等.机组组合在含风电系统的备用协调优化［J］.华东电力，2013，41(7):1481－1484.

［10］谢胤喆.引入风电机组的安全约束机组组合方法［D］. 杭州:浙江大学，2013.

［11］Wang J，Shahidehpour M，Li Z. Security－constrained unit commitment with volatile wind power generation［J］. IEEE Transactions on Power Systems，2008，23(3):1319－1327.

［12］Daneshi H，Srivastava A K. Security－constrained unit commitment with wind generation and compressed air energy storage［J］. IET Generation，Transmission ＆Distribution，2012，6(2):167－175.

［13］叶荣，陈皓勇，王钢，等.多风电场并网时安全约束机组组合的混合整数规划解法［J］.电力系统自动化，2010，34(5):29－33.

［14］谢胤喆，郭瑞鹏.考虑风电机组无功特性的安全约束机组组合方法［J］.电力系统自动化，2012，36(14):113－118.

［15］于芃，周玮，孙辉，等.用于风电功率平抑的混合储能系统及其控制系统设计［J］.中国电机工程学报，2011(17):127－133.

［16］谢毓广，江晓东. 储能系统对含风电的机组组合问题影响分析［J］.电力系统自动化，2011，35(5):19－24.

［17］高红均，刘俊勇，魏震波，等.基于极限场景集的风电机组安全调度决策模型［J］.电网技术，2013，37(6):1590－1595.

［18］陈海焱，陈金富，段献忠. 含风电场电力系统经济调度的模糊建模及优化算法［J］.电力系统自动化，2006，30(2):22－26.

［19］张晓花，赵晋泉，陈星莺. 含风电场机组组合的模糊建模和优化［J］.科技导报，2009(20):102－105.

［20］Chakraborty S，Senjyu T，Saber A Y，et al.A fuzzy binary clustered particle swarm optimization strategy for thermal unit commitment problem with wind power integration［J］. IEEE Transactions on Electrical and Electronic Engineering，2012，7(5):478－486.

［21］万振东，程浩忠，张建平，等.考虑风电消纳能力单目标及多目标模糊机组组合模型及应用［J］. 水电能源科学，2012，30(7):214－218.

［22］Venkatesh B，Yu P，Gooi H B，et al.Fuzzy MILP unit commitment incorporating wind generators［J］. IEEE Transactions on Power Systems，2008，23(4):1738－1746.

［23］刘宝碇，赵瑞清.随机规划与模糊规划［M］.北京:清华大学出版社，1998:74－94.

［24］Wang Q，Guan Y，Wang J. A chance－constrained two－stage stochastic program for unit commitment with uncertain wind power output［J］. IEEE Transactions on Power Systems. 2012，27(1):206－215.

［25］张宁宇，高山，赵欣.一种考虑风电随机性的机组组合模型及其算法［J］.电工技术学报，2013，28(5):22－29.

［26］Wang Q，Wang J，Guan Y.Price－based unit commitment with wind power utilization constraints［J］. IEEE Transactions on Power Systems，2013，28(3):2718－2726.

［27］Pozo D，Contreras J.A chance－constrained unit commitment with an n－Ksecurity criterion and significant wind generation［J］. IEEE Transactions on Power Systems，2013，28(3):2842－2851.

［28］Ding X，Lee W J，Jianxue W，et al. Studies on stochastic unit commitment formulation with flexible generating units［J］. Electric Power Systems Research，2010，80(1):130－141.

［29］刘宝碇，赵瑞清，王纲.不确定规划及应用［M］. 北京:清华大学出版社，2003:178－198.

［30］艾欣，刘晓，孙翠英. 含风电场电力系统机组组合的模糊机会约束决策模型［J］.电网技术，2011，35(12):202－207.

［31］熊虎，向铁元，陈红坤，等.含大规模间歇式电源的模糊机会约束机组组合研究［J］.中国电机工程学报，2013，33(13):36－44.

［32］Heitsch H，Römisch W. Scenario tree modeling for multistage stochastic programs［J］. Mathematical Programming，2009，118(2):371－406.

［33］Römisch W，Dupa ová J，Gröwe－Kuska N，et al.Approximations of stochastic programs.Scenario tree reduction and construction［C］//GAMS Workshop. Heidelberg. Berlin，Germany:DFG Research Center，2003:1 －3.

［34］Wang J，Botterud A，Bessa R，et al. Wind power forecasting uncertainty and unit commitment［J］. Applied Energy，2011，88(11):4014－4023.

［35］Høyland K，Wallace S W. Generating scenario trees for multistage decision problems［J］. Management Science，2001，47 (2):295－307.

［36］Heitsch H，Römisch W. Scenario reduction algorithms in stochastic programming［J］. Computational optimization and applications，2003，24(2－3):187－206.

［37］Growe－Kuska N，Heitsch H，Romisch W. Scenario reduction and scenario tree construction for power management problems［C］//Power Tech Conference Proceedings，2003 IEEE Bologna.Bologna，Italy:IEEE，2003:3－7.

［38］雷宇，杨明，韩学山. 基于场景分析的含风电系统机组组合的两阶段随机优化［J］.电力系统保护与控制，2012，40(23):58－67.

［39］Botterud A，Zhou Z，Wang J，et al.Unit commitment and operating reserves with probabilistic wind power forecasts［C］//2011 IEEE Trondheim PowerTech.Trondheim，Norway:IEEE，2011:1－7.

［40］张步涵，邵剑，吴小珊，等.基于场景树和机会约束规划的含风电场电力系统机组组合［J］. 电力系统保护与控制，2013，41(1):127－135.

［41］向萌，张紫凡，焦茜茜. 多场景概率机组组合在含风电系统中的备用协调优化［J］.电网与清洁能源，2012，28(5):61－69.

［42］Pappala V S，Erlich I，Singh S N. Unit commitment under wind power and demand uncertainties［C］//Power System Technology and IEEE Power India Conference.New Delhi，India:IEEE，2008:1－6.

［43］蒋凌，潘志，成天乐. 含风电电力系统旋转备用的鲁棒优化方法研究［J］.电力科学与工程，2013，29(04):1－6.

［44］魏韡，刘锋，梅生伟.电力系统鲁棒经济调度(二)应用实例［J］.电力系统自动化.2013(18):60－67.

［45］杨明，韩学山，王士柏，等.不确定运行条件下电力系统鲁棒调度的基础研究［J］.中国电机工程学报，2011，31(S):100－107.

［46］王冰，羊晓飞，李巧云. 基于坏场景集的抗风险鲁棒调度模型［J］.自动化学报，2012，28(02):270－278.

［47］高红均，刘俊勇，刘继春，等.基于坏场景集的含风电机组组合模型［J］.电力系统保护与控制，2013，41(10):27－32.

［48］陈皓勇，王锡凡.机组组合问题的优化方法综述(1)［J］. 电力系统自动化，1999，23(4):51－56.

［49］耿建，徐帆，姚建国，等.求解安全约束机组组合问题的混合整数规划算法性能分析［J］.电力系统自动化，2009，33(21):24 －27.［50］陈皓勇，王锡凡.机组组合问题的优化方法综述(2)［J］. 电力系统自动化，1999，23(5):51－56.

［51］何小宇，张粒子，谢国辉. 改进的拉格朗日松弛法求解机组组合问题［J］.电力系统保护与控制，2010，38(17):16－21.

［52］王燕涛，王大亮.计及风电的系统旋转备用容量的确定［J］.电测与仪表，2012，49(12):22－27.

［53］雷秀娟.群智能优化算法及其应用［M］. 北京:科学出版社，2012:87－89.

［54］江岳文，陈冲，温步瀛.含风电场的电力系统机组组合问题随机模拟粒子群算法［J］.电工技术学报，2009，24(6):129－137.

［55］Chakraborty S，Senjyu T，Saber A Y，et al. Optimal thermal unit commitment integrated with renewable energy sources using advanced particle swarm optimization［J］. IEEE Transactions on Electrical and Electronic Engineering，2009，4(5):609－617.

［56］Dang C，Li M. A floating－point genetic algorithm for solving the unit commitment problem［J］. European Journal of Operational Research，2007，181(3):1370－1395.

［57］Sun L，Zhang Y，Jiang C.A matrix real－coded genetic algorithm to the unit commitment problem ［J］. Electric Power Systems Research，2006，76(9－10):716－728.

［58］Senthil Kumar V，Mohan M R.Solution to security constrained unit commitment problem using genetic algorithm［J］. International Journal of electrical Power ＆ Energy Systems，2010，32 (2):117－125.