华北-华中特高压交直流线路相互作用解析分析
汪闻涛,徐 政,肖晋宇,王智冬
(1.浙江大学电气工程学院,杭州市310027;2.国网北京经济技术研究院,北京市102209)
0 引 言
2014年初哈密—郑州直流工程投产,落点在郑州地区,而华北电网与华中电网之间已有1 回长治到南阳的特高压交流线路相联,当哈郑直流发生双极闭锁时,将会引起受端大范围的潮流转移,尤其在长治—南阳特高压交流联络线潮流方向为华北送华中(南送)方式下,大量潮流将涌入华中电网,可能导致特高压交流联络线上功率头摆超过静稳极限,引起联络线两端系统功角失稳[1-5]。因此研究哈郑直流与长治—南阳特高压交流线路之间的相互作用机理,对提高华北—华中弱互联系统的稳定性具有重要的意义[6-10]。
文献[11-12]对长治—南阳特高压交流联络线功率波动进行了研究,分析了功率扰动后冲击功率的分配规律,建立了系统线性化模型,得到了功率波动峰值的计算公式。文献[13]在前两者的基础上,建立了不同阶段电网的动态模型,得到联络线功率波动的计算公式。上述文献主要针对功率扰动相对系统总负荷很小的情况,所以能够在系统平衡点附近建立线性化模型;而哈郑直流双极闭锁故障所造成的功率缺额占总负荷的比例将超过10%,不能采用平衡点附近的线性化模型进行分析。本文主要研究哈郑直流与长治—南阳特高压交流线路输送功率之间的关系,得到系统第1 摆的稳定裕度计算方法,推导临界状态下直流输送功率和交流联络线功率的代数关系。
1 交流系统间功角稳定性机理分析
1.1 系统简化分析模型
在实际电力系统中,华中电网分别通过哈郑直流和长治—南阳特高压交流线路与西北电网和华北电网相联。为了便于阐明稳定问题的物理本质,根据送受端电网结构对电网进行简化,得到如图1 所示的以华中电网为受端电网的简化分析模型。在该简化模型中,直流送端电网的内部机组用等值发电机Gs表示,其等值d 轴次暂态电抗为x'ds,送端电网内部负荷用等值负荷Ls表示;受端电网的内部机组用等值发电机Gr表示,其等值d 轴次暂态电抗为x'dr,受端电网内部负荷用等值负荷Lr表示;交流送端电网的内部机组用等值发电机Gj表示,其等值d 轴次暂态电抗为x'dj,内部负荷用等值负荷Lj表示;交流送受端电网之间的特高压交流联络线的阻抗为Xtie。
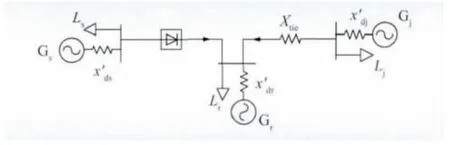
图1 系统简化分析模型Fig.1 Simplified analysis model
1.2 模型的数学表达
以图1 所示的简化分析模型为研究对象,分析特高压交流联络线功角稳定问题的物理机理。为了便于分析,对简化模型作如下假设。
(1)等值发电机均采用2 阶模型表示:
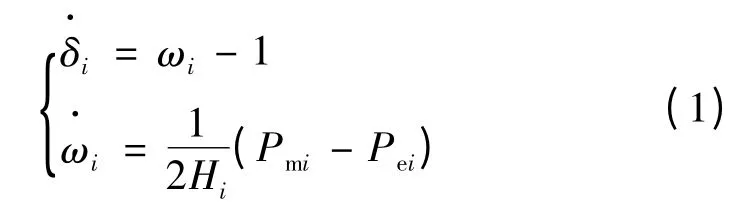
式中:δi、wi、Hi、Pmi、Pei分别为机组Gi的转子角、转速、惯性时间常数、机械功率、电磁功率。
(2)由于头摆失稳的暂态过程很短,发电机调速器动作不大,忽略等值发电机机械功率的变化,即假设Pms= Pms0、Pmr= Pmr0和Pmj= Pmj0。
(3)模型中各等值负荷均采用恒功率负荷模型表示。
1.3 直流闭锁故障过程的功角稳定性分析
根据简化模型,可以写出整个系统的动态特性方程组。因为交流受端电网的负荷功率为PLr,直流输电通道的输送功率为Pdc0,特高压联络线的输送功率为pac,因此交流受端电网等值发电机发出的电磁功率可以表示为
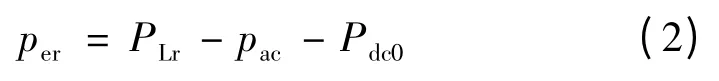
故受端电网等值机组的动态方程为
由于交流送端电网的负荷功率为PLj,因此交流送端电网等值发电机发出的电磁功率可以表示为

故交流送端等值机组的动态方程为

交流特高压联络线上输送功率最大值为

则特高压联络线上输送功率可以表示为
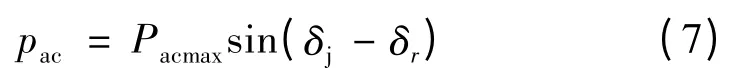
联立式(2)~(7),化简可得闭锁故障前送受端机组转子的相对转速的运动方程:
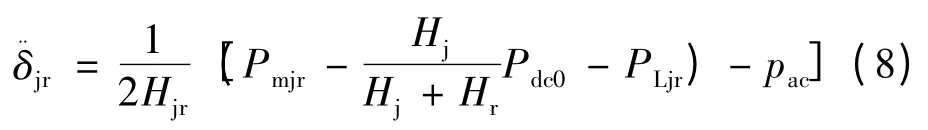
式中:
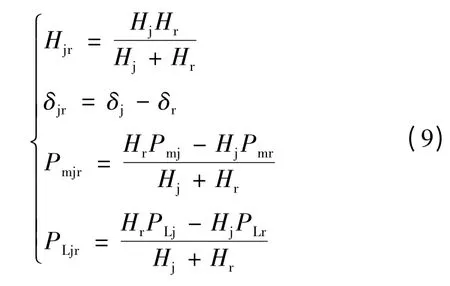
当直流系统发生双极闭锁故障时,特高压交流联络线上的输送功率pac随送受端机组功角差δ 变化的曲线如图2 所示。故障前特高压交流线路输送功率为Pac0,对应功角差为δ0;故障后系统趋于稳定时,特高压交流线路输送功率为Pac1,对应功角差为δ1。
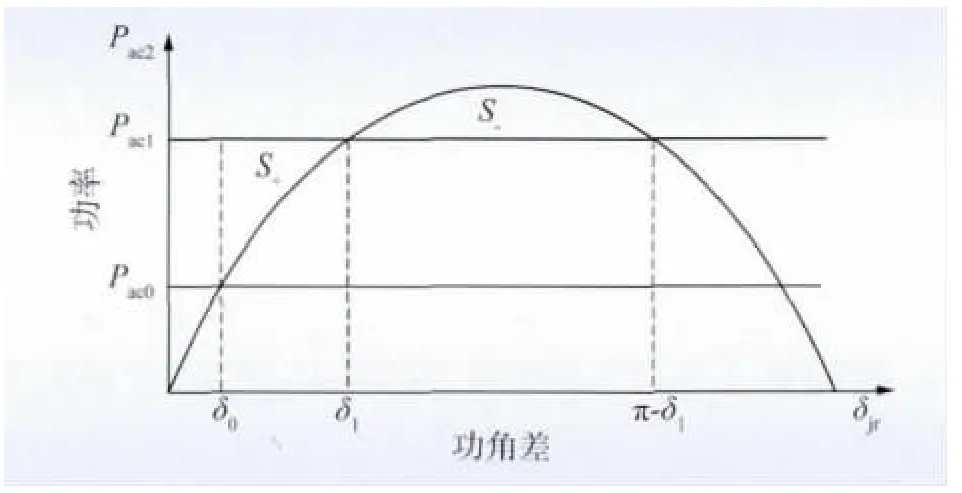
图2 交流输送功率随功角差变化曲线Fig.2 Variation curves of AC transmission power with power angle
故障前系统稳定的必要条件为式(8)右边等于0,由此得故障前稳定工作点处交流联络线上功率Pac0为
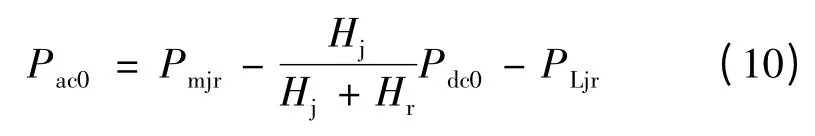
双极闭锁故障后,直流线路输送功率Pdc0为0,送受端机组转子相对转速的运动方程为
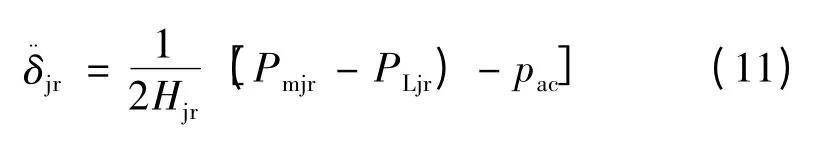
故障后系统若能恢复稳定,则式(11)右边等于0,可得故障后稳定工作点处交流联络线上功率Pac1为

故障后系统功角摇摆的过程为:
(1)故障前系统运行于稳定工作点δ0,特高压交流联络线输送功率为pac=Pac0。
(2)当直流发生双极闭锁故障后,直流线路输送功率Pdc0为0,送受端机组转子相对转速的运动方程由式(8)变为式(11)。由于转子的惯性,送受端功角差不能立刻由δ0跃升至δ1,此时pac< Pac1。由式(11)的运动方程可知δ¨jr>0 ,即送受端机组之间相对转速Δω 的导数大于0,因此功角差不断增大,Pac1与pac之间的差即为送受端转子相对转速的加速功率。
(3)当功角差到达δ1时,pac=Pac1,送受端之间相对转速Δω 的导数为0,但相对转速ω 仍大于0,于是功角差继续增加;
(4)当功角差越过δ1后,pac> Pac1,送受端之间相对转速Δω 的导数小于0,Δω 开始减小,pac与Pac1之间的差即为送受端转子相对转速的减速功率。若在功角差到达π-δ1之前,相对转速Δω 能够减为0,则系统能够在阻尼的作用下逐渐振荡回到稳定工作点δ1,若在功角差到π-δ1时,相对转速Δω 不能减小至0,送受端之间功角差将越过π-δ1,则送受端系统将发生功角失稳。
1.4 系统稳定性的敏感因素
图2 中功角差由δ0增加至δ1的过程中,Pac1与pac所围面积即为相对转速Δω 的加速面积S+,而功角差由δ1增加至π-δ1的过程中,pac与Pac1所围面积即为相对转速Δω 的最大减速面积S -。要使送受端之间不发生功角失稳,则减速面积S -与加速面积S+之差必须大于等于0。系统第1 摆的稳定裕度可以表示为
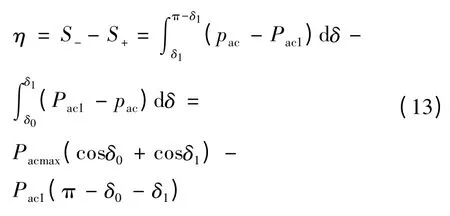
根据直流系统发生双极闭锁前的功率平衡条件,由式(7)得
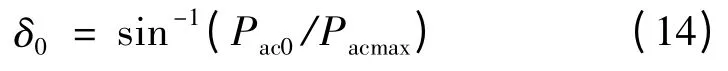
根据直流系统发生双极闭锁后的功率平衡条件,由式(7)得
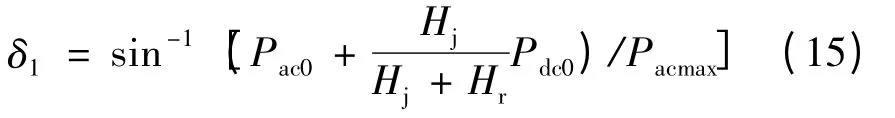
由式(14)可知δ0为Pac0和Pacmax的函数,由式(15)可知Pac1和δ1为Pac0、Pdc0和Pacmax的函数。因此,裕度η 的影响因素有Pac0、Pacmax和Pdc0。
将η 分别对Pac0、Pacmax和Pdc0求偏导,可得
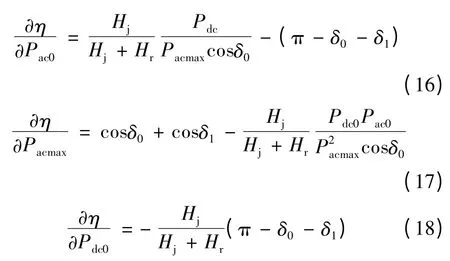
华北、华中电网在不同运行方式下的惯性时间常数比为1.1 ~1.5,即Hj/Hr为1.1 ~1.5。哈郑直流满送功率8 000 MW,南阳—长治特高压线路输送能力为5 000 MW,即Pdc0≤8 000 MW,Pac0≤5 000 MW,而Pacmax约为10 000 MW。根据式(14)、(15)可得δ0≤π/6,δ1<π/2。将各个量的取值范围代入式(16)~(18),可得
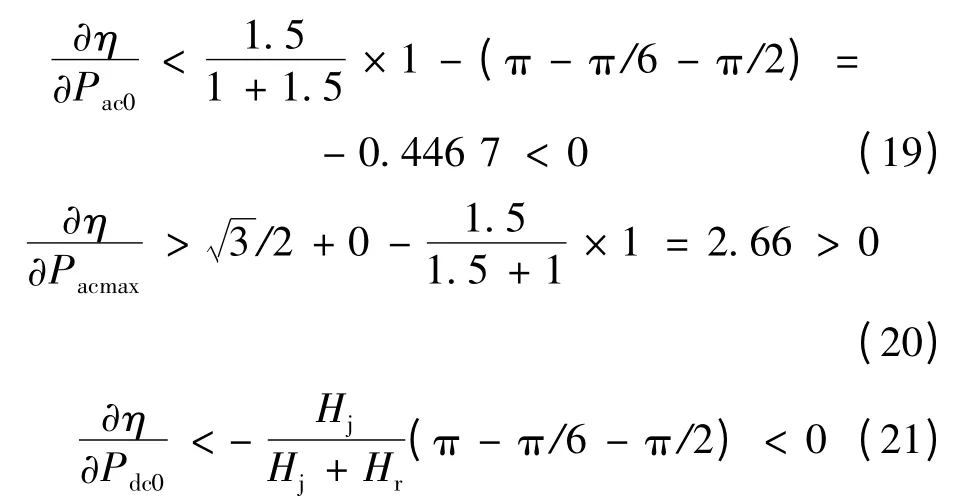
由此可知,当交流联络线上初始功率Pac0减小时,稳定裕度η 增大;当特高压交流联络线的极限输送功率Pacmax增大时,稳定裕度η 增大;当直流输电通道的输送功率Pdc减小时,稳定裕度η 也增大。
1.5 交直流通道极限输送功率的估算方法
当系统裕度η 为0 时,交流送端机组相对于受端机组的加速面积等于减速面积,此时系统处于恰好不失稳的临界状态,交流通道与直流通道的输送功率均达到极限值,通过式(13)可得
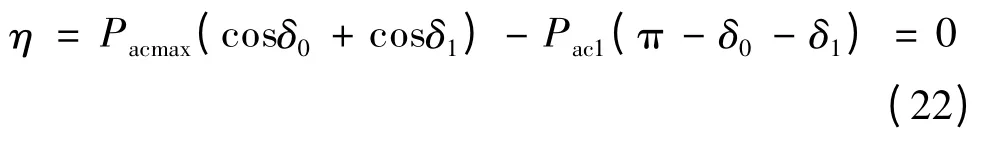
用故障前后稳定工作点的功角差δ0和δ1来表示,可得
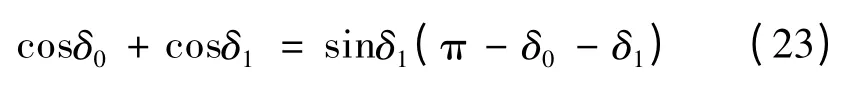
其中:

由式(23)、(24)可以求出临界状态下Pac0和Pdc0的数值关系。
2 交流系统间功角稳定性的数值计算分析
系统参数参考哈郑直流投产初期丰大方式下华中华北电网的规划数据,长治—南阳特高压交流工程南送功率为5 000 MW,哈郑直流丰大方式送电为8 000 MW。分别对交流送受端进行加权聚合等值,等值后系统参数(标幺值)如下:
交流送端E'j=1.136 5,Hj=3.649 2,x'dj=0.002 10。
交流受端E'r=1.121 0,Hr=3.185 6,x'dr=0.001 85。
特高压交流联络线Xtie=0.008 79。
为了分析临界状态下直流通道和交流通道输送功率的变化关系,令直流输送功率Pdc0由4 500 MW逐渐增加到8 000 MW,利用上面公式计算对应交流输送功率的Pac0极限值,Pac0随Pdc0的变化曲线如图3所示。
图4 所示为馈入受端系统的交流功率和直流功率之和随着直流功率变化的曲线,从中可以看出适当地增加直流功率Pdc0,减小交流功率可以增加输入受端电网的总功率。
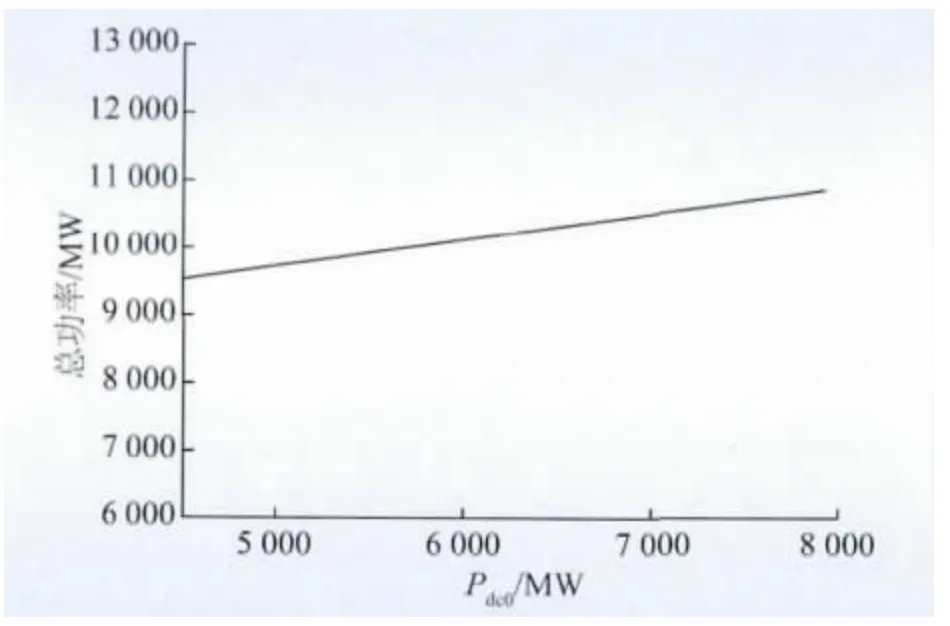
图4 输入受端总功率随Pdc变化的曲线Fig.4 Relationship between total input power and Pdc
3 仿真验证
为了验证图3 中的计算结果,利用哈郑直流投产初期丰大方式下华中华北电网的规划数据,采用逼近法,先固定直流输送功率Pdc0,然后逐渐改变Pac0,多次仿真求得Pac0的极限值。图5 中虚线为通过仿真得到的极限输送功率Pac0和Pdc0的关系,由图可知本文提出的交直流通道极限输送功率估算方法是较为准确的。
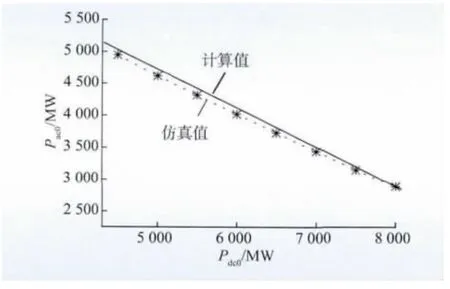
图5 计算值与仿真值的对比Fig.5 Comparisons between calculated values and simulation values
4 结 语
本文根据送受端电网结构建立了简化模型,分析了直流发生双极闭锁时交流联络线上功率随两端系统功角差变化的曲线,得到系统第1 摆的稳定裕度计算方法,分析了稳定裕度的敏感因素,得到临界值状态下直流输送功率和交流联络线功率的代数关系。通过与实际系统仿真结果的对比,验证了计算方法的有效性,并总结出交直流混合馈入系统的优化方案:适当减小交流联络线功率并提高直流输送功率可以提高输入受端电网的总功率。上述结论为电网安排送电方案提供了参考。
[1]赵良,郭强,覃琴,等.特高压同步电网稳定特性分析[J]. 中国电机工程学报,2008,28(34):47-51.
[2]易俊,孙华东,郭强,等.大型电源基地接入特高压输电系统方式研究[J].电网技术,2009,33(16):14-19.
[3]张健,张文朝,肖扬,等.特高压交流示范工程系统调试仿真研究及验证分析[J].电网技术,2009,33(19):29-32.
[4]高林,戴义平,马庆中,等.特高压线路解列后区域互联电网一次调频稳定性研究[J].电网技术,2009,33(20):27-32.
[5]舒印彪,张文亮.特高压输电若干关键技术研究[J]. 中国电机工程学报,2007,27(31):1-6.
[6]洪峰,陈金富,段献忠,等.弱互联大区电网联络线功率振荡研究[J].中国电机工程学报,2011,31(10):46-51.
[7]印永华,郭强,张运洲,等.特高压同步电网构建方案论证及安全性分析[J].电力建设,2007,28(2):1-4.
[8]孙昕,丁扬,印永华,等.中国特高压交流试验示范工程建设的基本原则[J].电力建设,2007,28(10):12-16.
[9]高宗和,陈刚,杨军峰,等.特高压互联电网联络线功率控制(一):AGC 控制策略[J].电力系统自动化,2009,33(15):50-55.
[10]朱方,赵红光,刘增煌,等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报,2007,27(1):1-7.
[11]刘辉,吴涛,李群炬,等.特高压交流示范工程功率摆动机制分析[J].中国电力,2010,43(7):9-13.
[12]汤涌,孙华东,易俊,等.两大区互联系统交流联络线功率波动机制与峰值计算[J].中国电机工程学报,2010,30(19):1-6.
[13]陈磊,刘辉,闵勇,等.两区域互联系统联络线功率波动理论分析[J].电网技术,2011,35(10):53-58.

