NO氧化反应速率常数与温度负相关原因的讨论

王家成 张树永

(山东大学化学与化工学院 山东济南250100)

从19世纪中叶开始，人们对于温度对反应速率的影响进行了比较系统的研究，发现速率常数(k)与温度(T)的关系主要有五种类型，见图1［1］。

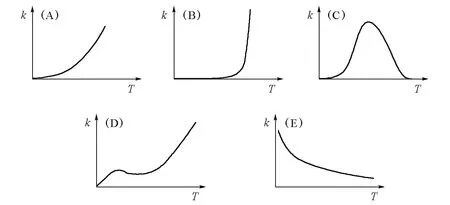
图1 反应速率常数(k)与温度(T)关系的5种主要类型

图1中的(A)型也称阿累尼乌斯(Arrhenius)型，其k～T关系符合阿累尼乌斯经验公式:

即:

图1中的(B)、(C)、(D)3种类型均不符合阿累尼乌斯公式;图1(E)型反应比较特殊，实例非常少见，最典型的例子是NO的氧化［2］:

1 基于简单反应的讨论

基于简单反应的讨论也可以称作基于NO2二聚体过渡态的讨论。

文献［3］将式(3)视为基元反应，并分别给出了其在600K和645K时k+1和k-1的数值，据此可以计算其正逆反应的活化能分别为Ea，+1=-1.196kJ·mol-1和Ea，-1=112.9kJ·mol-1。

上述数值与文献［4］报导的活化能-4.6kJ·mol-1并不相同，但活化能均为负值。负活化能与阿累尼乌斯定义的活化能矛盾，让人难以接受，这也是式(3)引发人们强烈好奇心的重要原因之一［5］。

研究表明［5-6］，在273～600K之间，式(3)的活化能为负值，其速率常数与温度的关系可表示为:

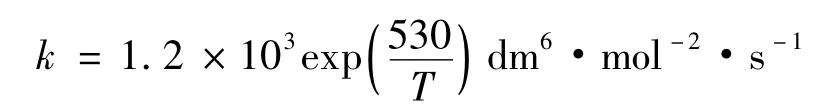
反应为三级反应，其活化能为-4.41kJ·mol-1。当温度超过650K时，活化能变为正值。

如果假设式(3)为三分子基元反应(termolecular reaction)［5-6］，经过过渡态［ONOONO，则反应过程可表示为:

理论计算表明，该反应的活化能为负值［5］。因式(4)所示机理无法解决负活化能这一令人费解的现象，因此，人们更倾向于采用两步反应来解释［6］。

2 基于NO二聚体中间体的讨论

有实验证明反应过程中存在(ON┈NO)中间体。已知NO分子的电子排布为(σ1s)2(σ1s*)2(σ2s)2(σ2s*)2(σ2p)2(π2p)4(π2p*)1［7］，其π2p*轨道上有一成单电子，故NO的性质类似自由基［8］，容易相互结合形成二聚体(ON┈NO)。该二聚体有顺式(cis-)和反式(trans-)两种构型［9］。故有人提出式(3)实际上是一个复杂的连串反应，目前被广泛接受的机理是［1-2，5-6］:

采用速率控制步骤近似和平衡近似原理［1-2］，可以导出其速率方程:

式(6)表明式(3)为三级反应，与实验事实一致［5］。由式(6)可得出反应的表观活化能(Ea，app)为:

根据反应活化能估算的经验规则［4，10］，机理(式(5))中第一步反应的正反应属于自由基结合，其Ea，1的数值很小甚至为0，而其逆反应活化能Ea，-1等于破坏(ON┈NO)二聚体中相互作用所需的能量，应该具有比较大的数值。这似乎表明该平衡应该偏向右侧，但有文献报导［6］，在298K时，第一步平衡只有0.0065%的NO以二聚体形式存在，说明二聚体的浓度很低。测量和理论计算均表明，二聚体的结合能并不高［9，11-15］，大约在8.37［9］～11.95kJ·mol-1［11］之间，也有报导为6.47kJ·mol-1［15］。因此，第一步反应中的正反应和逆反应均应属于快反应;而由式(7)可知Ea，2＜Ea，-1，故第二步反应的活化能也非常小，也应为快反应。

要使式(3)的Ea，app＜0，只需满足Ea，-1＞Ea，2+Ea，1即可。式(3)的表观活化能与式(5)对应的各基元反应活化能之间的关系示于图2。

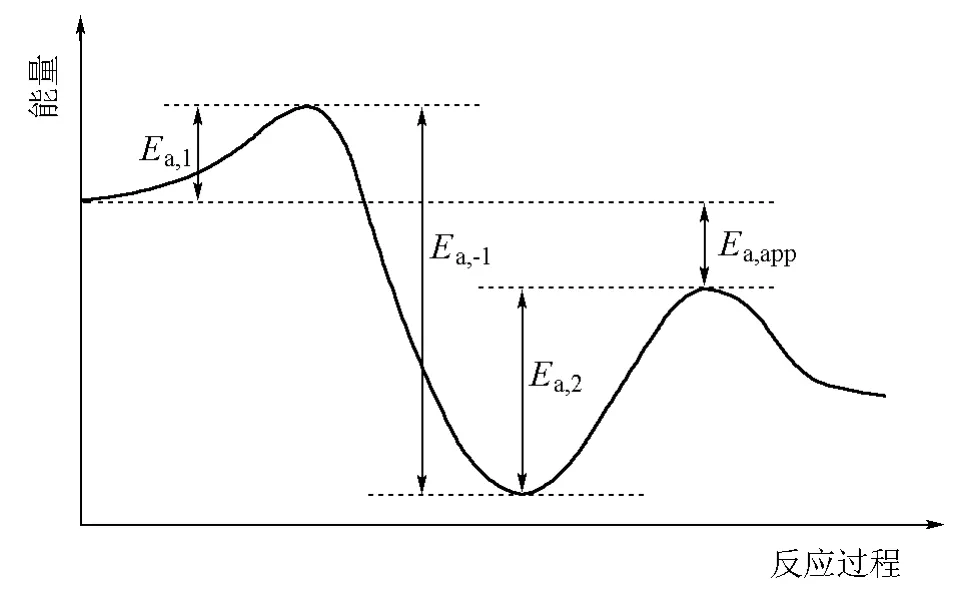
图2 NO氧化反应表观活化能与各基元反应活化能的关系

图2 显示，机理(式(5))中第一步是放热的可逆反应，但放热不大。当温度升高时，该平衡左移致［(NO)2］减小。由式(6)可知，［(NO)2］的减小会导致降低，从而出现式(3)的速率常数随温度升高而降低的现象［2］。

以上讨论表明，采用式(5)所示机理，通过速率控制步骤近似和平衡近似并结合平衡移动原理，可以比较圆满地解释NO氧化反应的速率常数随温度升高而降低这一“反常”现象。同时也说明，式(3)的活化能只是表观活化能，没有确切的物理意义，其大小取决于3个相关基元反应活化能的相对大小，而所有基元反应的活化能均为正值，不存在活化能为负的“反常”现象，故式(5)更易为人接受［1-2］。

虽然上述讨论对式(3)负活化能现象给出了合理解释，但该讨论在推导过程中却忽视了一些前提假设的正确性。例如，如果Ea，app＜0，必然有Ea，-1＞Ea，2和k-1＜k2［O2］，这不符合平衡近似处理的条件(表1)［1］，故采用平衡近似求解［(NO)2］并不可靠。

表1 对式(5)进行近似处理的条件分析

如果采用稳态近似方法处理式(5)，可以得到如下速率方程［6］:

式(8)表明该反应没有确定级数，表观活化能与各基元反应活化能之间也不存在对应关系。当k-1≫k2［O2］(即满足平衡近似条件)时，式(8)可化简为式(6)。但由图2可知，此处Ea，1＜Ea，2，即NO二聚体的消耗速率小于其生成速率，故对NO二聚体进行稳态近似处理的条件也不存在了(表1)。

另外，作为速率控制步骤近似的条件，第二步反应的活化能应较第一步高10kJ·mol-1以上，对于式(5)也很难满足这一要求。因此，采用常用的速率控制步骤近似、稳态近似和平衡近似来处理式(5)所示机理并不合理。而不经近似处理直接求解式(5)的难度很大，且无法得出令人满意的结论［16］。

3 基于NO3中间体的讨论

为解释式(3)，人们还提出了其他机理［5-6］，如:

在该机理中，NO可以看作自由基，而NO3也具有自由基的性质［14］。第一步反应的正反应活化能(Ea，+)较小，其逆反应涉及作用的破坏，应具有较高的活化能(Ea，-1)。第二步反应涉及N┈O和O—O键的断裂，所以活化能(Ea，2)较大，可以作为速率控制步骤。有关活化能的讨论可以仿照第2部分的讨论;对NO3进行速率控制步骤近似和平衡近似处理可以直接得出式(6)，如果采用稳态近似处理可以先得到式(8)，再在k-1≫k2［O2］的条件下转化成式(6)［6］。

因此，式(9)所示机理同样可以说明式(3)为三级反应，表观活化能为负值，速率常数随温度升高而下降等实验事实。而且从活化能和速率的角度分析，式(9)所示机理比式(5)更具合理性［6］。

这里必须说明，无论式(4)、式(5)还是式(9)都有其合理性［6］，但也都有其不合理的地方，因此有关式(3)的研究还远称不上完善［4］。

［1］印永嘉，奚正楷，张树永.物理化学简明教程.第4版.北京:高等教育出版社，2007

［2］Chang R.Physical Chemistry for the Chemical and Biological Science.California:University Science Books，2000

［3］杨永华.物理化学.北京:高等教育出版社，2012

［4］傅献彩，沈文霞，姚天扬，等.物理化学.第5版.北京:高等教育出版社，2006

［5］Gadzhiev O B，Ignatov S K，Razuvaev A G，et al.J Phys Chem A，2009，113(32):9092

［6］Tsukahara H，Ishida T，Mayumi M.Nitric Oxide，1999，3(3):191

［7］朱万强，罗宿星，李华刚，等.大学化学，2013，28(1):23

［8］Lund A，Shimada S，Shiotani M.Principles and Applications of ESR Spectroscopy.New York:Springer，2011

［9］Marouani S，Bahri M，Batis H，et al.J Phys Chem，2010，114(9):3025

［10］Hu Y.Physical Chemistry.Beijing:Higher Education Press，2013

［11］Pedro P S，Jesus R S，Ramon H L.J Phys Chem A，2011，115:2892

［12］Tobita M，Perera S A，Musial M，et al.J Chem Phys，2003，119:10713

［13］Wade E A，Cline J I，Lorenz K T，et al.J Chem Phys，2002，116:4755

［14］Morris V R，Bhatia S C，Hall J H Jr.J Phys Chem，1990，94(19):7414

［15］Gadzhiev O B，Ignatov S K，Gangopadhyay S，et al.J Chem Theor Comput，2011，7:2021

［16］Wesley W B.J Math Chem，2011，49(2):328