一种测斜仪安装位置误差补偿方法
潘 萌,程为彬,贾宏亮,区广宇,金 金
(1.西安石油大学电子工程学院,陕西西安 710065;2.中国石油集团测井有限公司技术中心,陕西西安 710077;3.陕西省天然气股份有限公司,陕西西安 710016)
0 引 言
全角度旋转导向钻井中,准确测量井下钻具姿态参数,即井斜角I、工具面角T、方位角A是实现井下全角度导向钻井的关键因素.
姿态测量系统中存在各类误差,如零位误差、位置误差(包括安装误差)、标度因子误差、温度漂移误差、传感器测量误差和数据处理误差等,其中结构安装产生的位置误差占到整体误差的70%[1].理论上,测斜仪各轴组成的仪器坐标系应与地理坐标系各对应轴线相重合.实际上,由于安装上的原因,即使精心调校,也不可避免地存在测斜仪各轴与理想坐标各轴不重合而引起的位置误差.由此传感器各轴间产生的不正交度是影响总精度的重要指标,对最终的测量结果有着不可忽视的影响.
对姿态传感器测量结果进行处理时采用的最小二乘法[2]、共轭梯度法[3]、最大似然法[4]、卡尔曼滤波法[5]、蒙特卡罗法[6]、神经网络法[7]等算法,以及它们的改进算法,主要适合随机误差的处理,对位置误差等系统误差的处理难以奏效.文献[8]对姿态传感器的位置误差进行建模时存在缺陷,假定地理坐标系S轴和仪器坐标系初始Z轴重合,这本身就忽略了这两个轴的轴不重合误差.文献[9]对测量结果处理时前提条件不严谨,引入了方法误差,降低了校正精度.文献[10]定义3个轴的相对误差角,提出由理想坐标系到实际仪器坐标系的三轴旋转概念,但随之又忽略二阶和三阶分量,产生新的方法和计算误差.文献[11]分析安装误差产生的原因,同样定义了3个轴的相对误差角,给出包含各类误差的统一模型,但产生机理和欧拉旋转变换分析不清晰.为克服上述现有姿态测量系统中位置误差模型和补偿方法的不足,本文建立一种基于正交旋转变换的位置误差模型,提出更为简便的系数补偿方法,对姿态参数进行校正.
1 姿态参数的计算
根据实际加速度计传感器安装方向,选取如下两个坐标系,北西天地理坐标系(ONWS)和仪器坐标系(OXYZ).两个坐标系初始是重合的,ON在当地水平面内指北,OW在当地水平面内指西,OS沿当地地垂线方向指天,与OW,ON组成右手坐标系.钻井过程中,仪器坐标系(OXYZ)是北西天坐标系(ONWS)经过一系列转动得到的.根据旋转变换中的欧拉定理,测斜仪在空间中的姿态可用相对于地理坐标系有限次的转动来表示.将地球重力加速度g向仪器坐标系上投影,可得3轴加速度计输出为[12]

式中:g x,g y,g z为加速度计在XYZ方向的分量输出.
可得井斜角和工具面角为

2 测量模型与补偿方法
位置误差使旋转得到的仪器坐标系的XYZ轴均存在I x,I y,Iz,T x,T y,T z的非正交度.将传感器3轴看成3个独立的空间轴,通过包含3个实轴的理想正交坐标系的多次坐标变换,得到包含各自位置误差在内的旋转矩阵.
首先,将理想的仪器坐标系OXYZ绕OYx轴旋转角I x到,再绕轴旋转角Tx到,最后得到的一个实际正交仪器坐标系,其中的轴构成实际测量仪器坐标系的X轴.旋转过程如图1所示.
则该坐标系下测量输出为
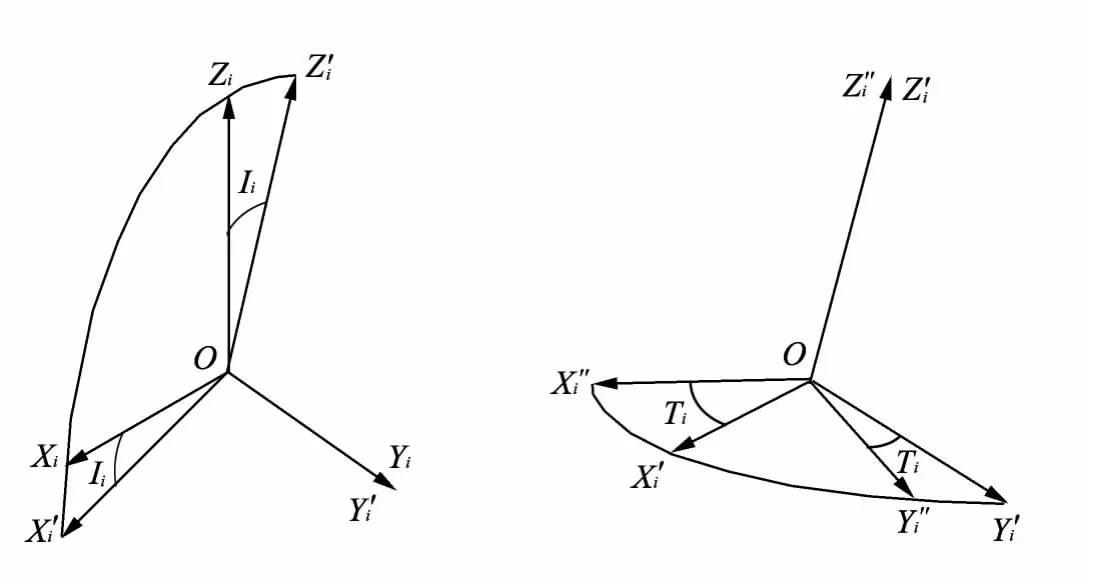
图1 正交坐标系旋转变换(i=x,y,z)Fig.1 Orthogonal coordinate transmission

该坐标系中g yy输出为实际仪器坐标系下Y实轴的真实输出.正交仪器坐标系OX″z Y″z Z″z下测量输出为
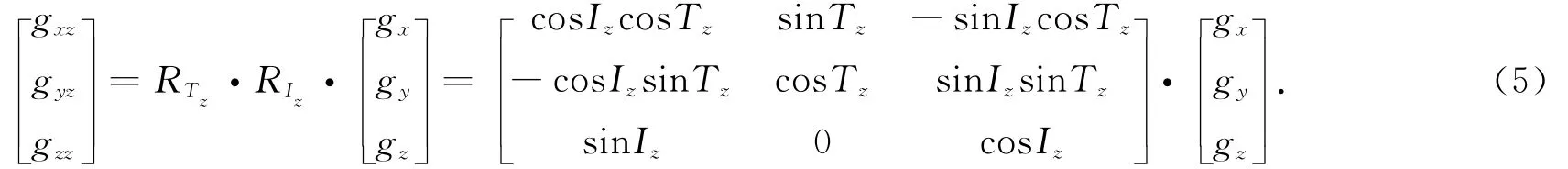
该坐标系中g zz输出为实际坐标系下Z实轴的真实输出.将式(3)~式(5)中的X,Y,Z实轴测量输出抽出,构成一个新的矩阵,可表示为
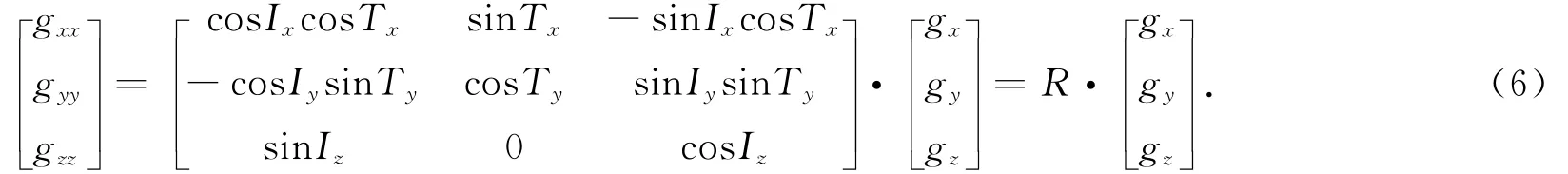
可以通过一些特殊位置的测量值和理论值获得相应的矩阵系数,得到误差矩阵R,对R求得逆矩阵R-1,即补偿矩阵.正常姿态测量过程中就可通过补偿矩阵得到任意姿态下3轴测量传感器的解耦、补偿校正结果.

3 实验数据校正与分析
3.1 工具面角校正前后对比
首先利用式(2)对传感器输出信号解算,得到校正前的工具面角值;再利用补偿矩阵R-1对原信号校正,得到校正后的工具面角值.分别对校正前后的原数据进行线性拟合,得到各自的拟合方程.刻度井斜角I=1.5°,3.5°,58.5°和88.5°时,计算工具面角校正前后的数据对比如图2中(a),(b),(c),(d)所示.其中,横轴为测试台刻度工具面(0~360°,间隔5°),纵轴为计算工具面角.
图2中R2是趋势线拟合度的指标,也称为相关系数,其数值大小反应趋势线的估计值与对应的实际数据之间的拟合度越高,趋势线可靠性越高.R2是取值范围在0~1之间的数值,当R2等于1或接近1时,其可靠性较高,反之则可靠性较低.对于工具面的校正,拟合结果应是线性方程,所以R2越接近1,校正结果越理想.
由图2可知,各理论井斜角下,校正前计算工具面角的R2分别为0.921 0,0.994 7,0.999 9,0.999 9;校正后R2分别为0.994 3,0.998 2,1.000 0,1.000 0.可知校正后R2更接近或等于1,说明工具面角的实际数值与趋势线的估计值之间的拟合程度高,达到了很好的校正效果.
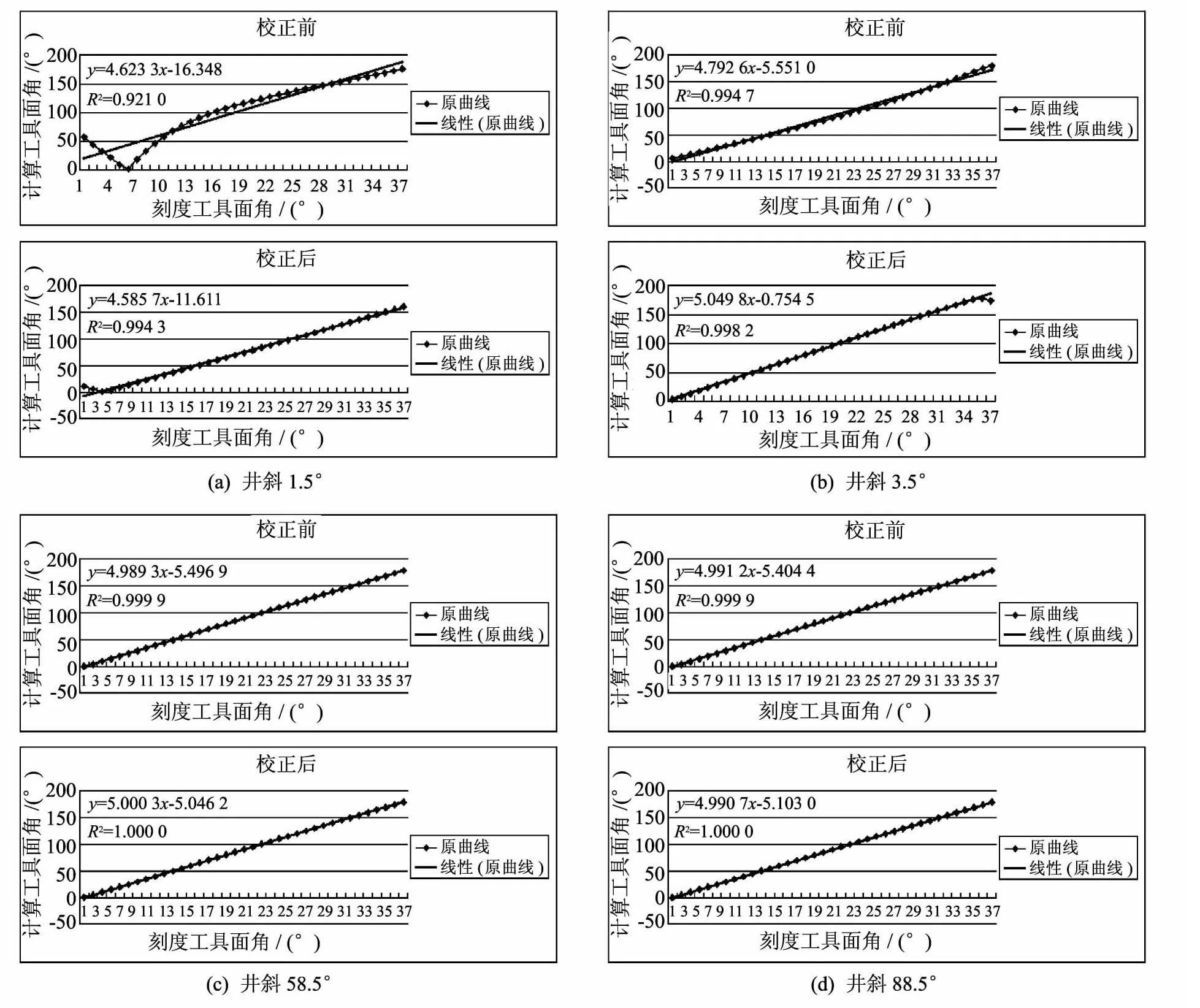
图2 工具面校正前后的数据对比Fig.2 Data comparison of tool face angle with no correction and correction
3.2 井斜角校正前后对比
首先利用式(2)对传感器输出信号解算,得到校正前的井斜角值;再利用补偿矩阵R-1对原信号校正,得到校正后的井斜角值.刻度井斜角I=1.5°,3.5°,58.5°和88.5°时,计算井斜角校正前后的数据对比如图3中(e),(f),(g),(h)所示.其中横轴为测试台刻度工具面(0~360°,间隔5°),纵轴为计算井斜角.
根据图3得到的解算结果求出各理论井斜角的井斜平均值、绝对误差、相对误差及方差,结果如表1所示.
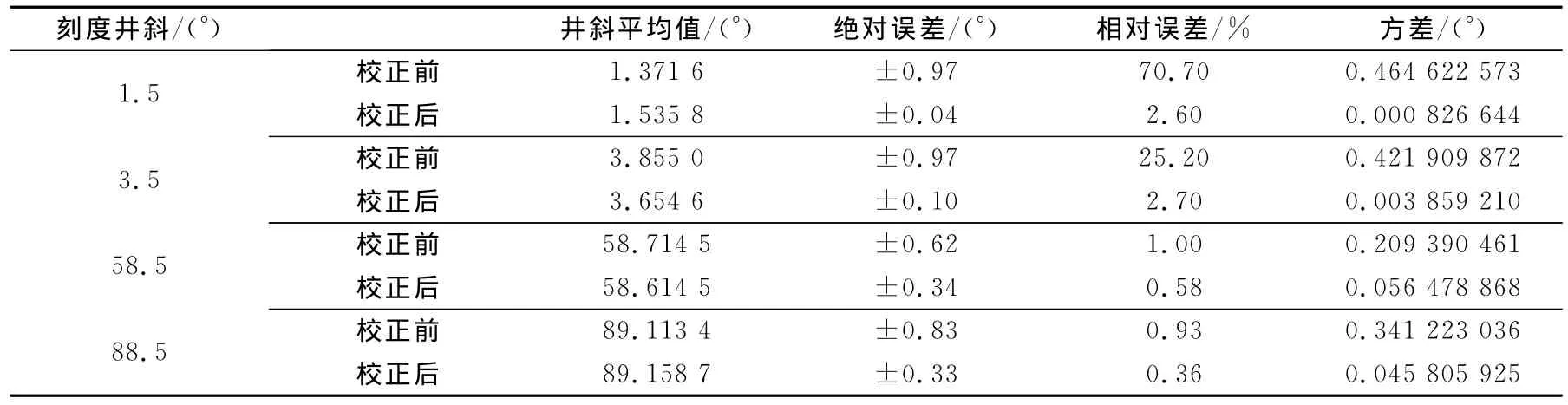
表1 井斜校正前后对比Tab.1 Comparison of inclination angle with no correction and correction
由表1可知,采用系数补偿法校正后,4组计算井斜角的绝对误差从±0.97°~±0.62°降低到±0.04°~±0.34°,说明该方法在应用中产生了效果.四组计算井斜角的相对误差从70.70%~0.93%降低到2.6%~0.36%,说明在全角度范围内,校正效果整体提高了,基本上实现了等精度;同时4组计算井斜角校正后的方差平均降低一个数量级以上.校正前后误差的散点分布如图4所示.
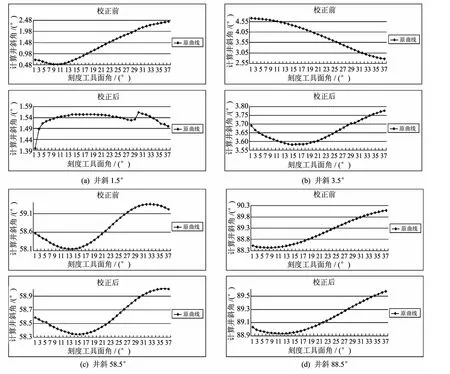
图3 井斜校正前后数据对比Fig.3 Data comparison of inclination angle with no correction and correction
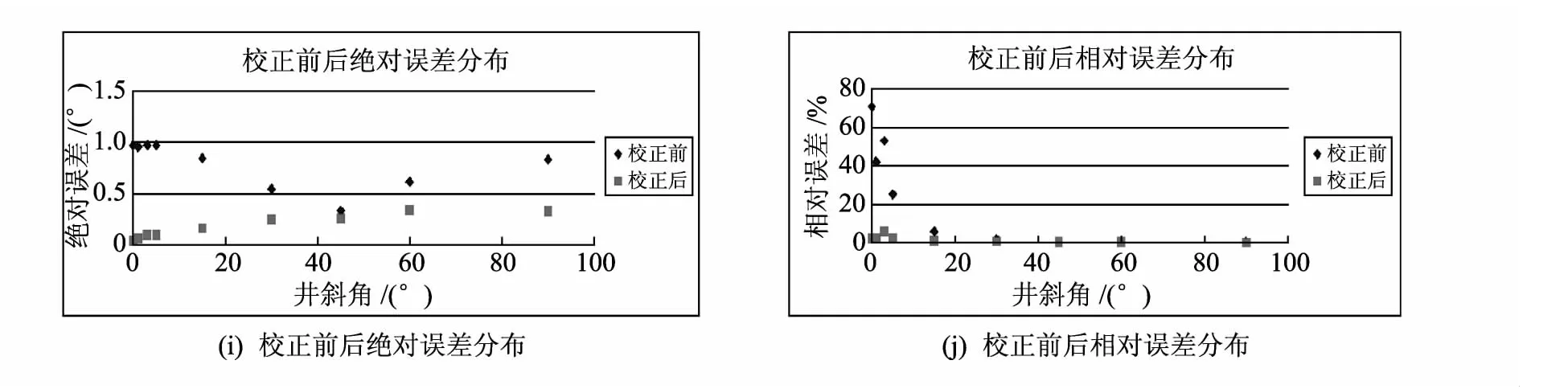
图4 井斜校正前后误差分布Fig.4 The error distribution of inclination angle with no correction and correction
4 结 论
采用系数补偿法对姿态参数校正后,各工具面角的实际数值与趋势线的估计值之间的拟合程度高.各井斜角的相对误差明显减小了,基本实现了等精度,而且各井斜角的方差平均降低一个数量级以上,达到了较理想的校正效果.但在确定补偿矩阵的过程中,未考虑零位误差、刻度因子误差等因素的影响,因此还需要进一步优化,以期达到更好的校正效果.
[1] 乔红兵,郭继坤.钻井测斜仪的误差分析[J].煤矿机械,2003(8):41-43.
Qiao Hongbing,Guo Jikun.The error analysis on clinometer of drilling[J].Coal Mine Machinery,2003(8):41-43.(in Chinese)
[2] 崔敏,马铁华,张慧,等.基于十二加速度计的GFSINS安装误差标定及补偿[J].中国惯性技术学报,2009,17(4):413-417.Cui Min,Ma Tiehua,Zhang Hui,et al.Calibration and compensation for installation errors of GFSINS with twelve-accelerometers[J].Journal of Chinese Inertial Technology,2009,17(4):413-417.(in Chinese)
[3] 胡海滨,林春生,龚沈光.基于共轭次梯度法的非理想正交三轴磁传感器的修正[J].数据采集与处理,2003,13(1):88-91.
Hu Haibin,Lin Chunsheng,Gong Shenguang.Correction of incompletely orthogonal three axial magnetic sensor by conjugated approximate gradient algorithm[J].Journal of Data Acquisition &Processing,2003,13(1):88-91.(in Chinese)
[4] Vasconcelos J F,Elkaim G,Silvestre C,et al.Geometric approach to strapdown magnetometer calibration in sensor frame systems[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2):1293-1306.
[5] Creagh Michael A,Beasley Peter,Dimitrijevic Igor,et al.A kalman-filter based inertial navigation system processor for the SCRAMSPACE 1 hypersonic flight experiment source[C].18th AIAA/3AF International Space Planes and hypersonic Systems and Technologies Conference 2012,2012:1969-2014.
[6] 朱国力,文香稳,潘明华.三维姿态测量系统的安装误差[J].华中科技大学学报(自然科学版),2011,39(5):1-5.
Zhu Guoli,Wen Xiangwen,Pan Minghua.Installation errors of three-dimension pose measurement systems[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2011,39(5):1-5.(in Chinese)
[7] 吴德会,黄松岭,赵伟.基于FLANN的三轴磁强计误差校正研究[J].仪器仪表学报,2009,30(3):449-453.
Wu Dehui,Huang Songling,Zhao Wei.Research on correction of tri-axial magnetometer based on FLANN[J].Chinese Journal of Scientific Instrument,2009,30(3):449-453.(in Chinese)
[8] 吴俊伟,李绵伟,王小旭,等.无陀螺捷连惯导系统的安装误差辨识方法[J].测试技术学报,2008,22(5):412-418.
Wu Junwei,Li Mianwei,Wang Xiaoxu,et al.An identification method for installation errors of GFSINS[J].Journal of Test and Measurement Technology,2008,22(5):412-418.(in Chinese)
[9] 覃方君,许江宁,傅军,等.一种简化的无陀螺惯导系统安装误差校准方法[J].测试技术学报,2008,22(2):155-159.
Tan Fangjun,Xu Jiangning,Fu Jun,et al.A simplified installation error calibration method for gyro-free inertial navigation systems[J].Journal of Test and Measurement Technology,2008,22(2):155-159.(in Chinese)
[10] 陈娟,尹立鹏,丁宁.加速度计安装角误差实验分析[J].长春工业大学学报(自然科学版),2010,31(4):442-445.
Chen Juan,Yin Lipeng,Ding Ning.Experimental analysis of accelerometer installation error[J].Journal of Changchun University of Technology(Natural Science Edition),2010,31(4):442-445.(in Chinese)
[11] 杨常松,徐晓苏.捷联惯导系统加速度计标度因数和安装误差的试验标定[J].测控技术,2005,24(12):57-59.
Yang Changsong,Xu Xiaosu.Calibration of scale factor &installation error coefficients of accelerometers in strapdown navigation system[J].Measurement &Control Technology,2005,24(12):57-59.(in Chinese)
[12] 周云凤.旋转导向钻井工具全角度姿态测量与解算技术研究[D].西安:西安石油大学,2010.

