基于新型相位载波调制解调技术的双M-Z光纤振动传感器
林文台,娄淑琴,梁 生
(1.北京交通大学电子信息工程学院,北京 100044;2.北京交通大学物理系,北京 100044)
0 引 言
分布式光纤扰动传感器(FDDS)在周界安防、输油管道预警等国防、能源领域有着广泛的应用.目前国内外针对分布式扰动传感器有多种方案,主要3类,包括光时域反射式方案、光纤光栅阵列方案和干涉仪型方案.其中,光时域反射式方案具有很高的空间分辨率,但不适用于高频信号的振动传感,并且实时性差,限制了其在实际中的应用[9];光纤光栅阵列方案实现了准分布式传感,但存在监测距离的限制,由于光栅复用数量有限,不适用于长距离应用的要求[10].基于M-Z干涉仪的FDDS具有灵敏度高、定位算法简单、定位精度高等优点,适用于长距离传感应用,成为了光纤分布式传感的主流技术方案[1-8].
基于双M-Z干涉仪的FDDS在实际应用中,由于其光路结构的非互易性和不均匀温度场分布,M-Z干涉仪的相位发生随机漂移,从而导致传感器产生定位误差,甚至导致定位失败.
因此,本文提出了一种基于新型PGC技术的双M-Z干涉仪,它针对长距离双M-Z型FDDS的特点,巧妙利用窄带模拟低通滤波器,解决了窄带数字低通滤波器难以硬件实现的问题;构造了特殊的本地解调项,解调了信号中的高次谐波;消除了低频相位漂移和载波相位延时的影响,提高了信噪比,从而显著提高了定位精度.

图1 采用新型PGC技术的双M-Z型FDDS原理框图Fig.1 Schematic illustration of FDDS with a PZT
1 系统原理
采用新型PGC技术的双M-Z型FDDS的原理框图如图1所示.
为了消除相位漂移,在靠近耦合器B端引入PZT相位调制器.调制信号表达式为

式中:C为调制深度;ω0为调制信号的角频率.
调制后,顺时针及逆时针方向M-Z干涉仪的干涉信号表达为
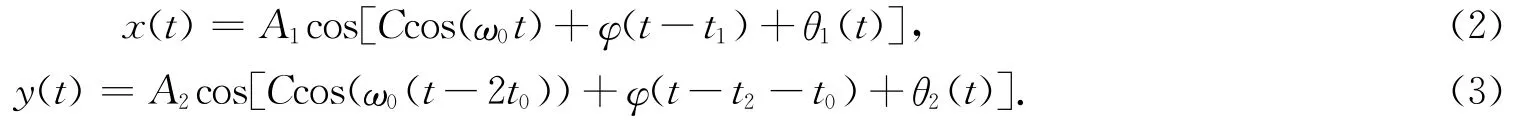
以x(t)为例分析调制信号的频谱,将x(t)用Bessel函数展开,可得

式中:k为整数,φ(t)=φ(t-t1)+θ1(t).
1.1 PGC调制

图2 调制后信号频谱分布图Fig.2 Frequency spectrum of modulated signal
由式(4)可以看出,调制后信号的频谱包括载波信号的各次谐波及其边带上信号的各次谐波,如图2所示.为了实现无混叠采样,理论上要求采样频率为无穷大,这在实际使用中是无法实现的.但是依据贝塞尔函数的性质,信号的主要频谱成分集中在有限的频带内,当指定了系统指标之后,可以根据需要的频谱成分来滤除不需要的高次谐波及其边带信号.
为了保证调制过程中频谱不重叠,必须使调制频率ω02kωs,其中ωs为振动信号的角频率.在双M-Z型FDDS中,振动信号和传统PGC中研究的小信号不同,其幅值为0.1 V~3 V,信号带宽为2 k Hz,根据Bessel函数的分布规律可知,其主要频谱分量集中在20ωs内,即40 k Hz,为了保证解调信号的准确度,此时取边频分量k=25,因此,载波的调制频率设置为100 k Hz.
1.2 PGC解调
传统数字式PGC技术解调算法流程如图3所示.
采用传统数字式PGC技术解调算法存在以下几个问题:①由于需要实现100 m的定位精度,则要求采用1 MHz采样率,高采样率下的窄带数字滤波器(40 k Hz)在硬件上实现难度大,阶数高,滤波效果差,导致了信号失真和信噪比下降.②采用cos(ω0t)和cos(2ω0t)作为混频信号,其解调的谐波次数为3,而双M-Z型FDDS中为保证振动信号的频率分量不损失,需要解调高次(5次)谐波分量,谐波次数的下降导致了信号信噪比的下降[11-15].③传统数字式PGC技术解调算法中对调制深度的要求较高,调制深度的漂移会导致解调信号幅度的不稳定,一般取C=2.37,降低调制深度的变化对解调信号幅度的影响[11].④传统数字式PGC技术解调算法中因传导光纤很短,忽略了传导光纤引入的载波时延对解调结果的影响,而双M-Z型FDDS中的时延为2t0,引入解调幅度变化项cos(2ω0t0)cos(4ω0t0),导致解调信号幅度漂移,信噪比下降,甚至解调信号被噪声淹没.

图3 传统数字式PGC解调算法流程图Fig.3 Schematic illustration of conventional PGC
因此,传统数字式PGC技术解调算法无法高保真恢复振动信号,并且其解调结果不稳定,信噪比较低,导致了定位误差.
为了克服传统数字式PGC技术在双M-Z型FDDS中解调能力的不足,本文提出了新型PGC技术,其解调流程如图4所示.

图4 新型PGC解调算法流程图Fig.4 Schematic illustration of novel PGC
以干涉信号x(t)为例进行解调分析.x(t)与混频信号cos[Ccos(ω0t)]和sin[Ccos(ω0t)]进行混频,混频后结果为

混频信号经模拟低通滤波后的输出为

二者微分后的结果为

微分前后的结果交叉相乘并相减后得到

再经积分后可以得到

式中:φ(t)=φ(t-t1)+θ1(t),θ1(t)为低频相位漂移,可通过高通滤波器去除,高通后得到最终的解调输出结果为

对于y(t),其解调流程完全一致,最后得到解调结果为

和传统数字式PGC技术比较,新型PGC技术解调算法做了以下改进:①采取先模拟后数字的方法,在混频之前采用模拟乘法器,这样可以消除采样率的限制,滤波效果的提升直接改善了信号的信噪比.② 采用cos[Ccos(ω0t)]和sin[Ccos(ω0t)]进行混频,而不是采用cos(ω0t)和cos(2ω0t),这样可保证解调至5次谐波,从而提高了信号的信噪比.③采用cos[Ccos(ω0t)]和sin[Ccos(ω0t)]进行混频,使得最后的解调结果和调制深度无关,消除了因调制深度变化导致的解调结果不稳定.④逆时针M-Z干涉仪的输出解调时考虑了传导光纤引入的时延2t0,采用cos[Ccosω0(t-2t0)]和sin[Ccosω0(t-2t0)]进行混频,从而补偿了传导时延对解调结果的影响.
利用x(t)和y(t)的解调结果式(13)和式(14)进行时延计算,即可准确得到振动点的位置L1.
2 实验与讨论
2.1 实验内容

图5 实验中控制温箱Fig.5 Photograph of experimental setup with temperature controllable ovens(TCOs)
实验中,采用40 km光纤搭建M-Z分布式光纤扰动传感器.利用温箱模拟温度变化,加强非互易性初始相位现象.
1)实验1:测试非互易性引起的定位误差.在实验中,传感光纤1和2所在温箱保持温度稳定在25℃,保温时间为1 h;非稳定温度场实验中,传感光纤A所在温箱由-40℃升温至60℃,升温时间为1 h,而传感光纤B所在温箱温度保持25℃.在两种情况下,在L1=0和24.52 km处进行扰动,分别测试10次.
2)实验2:测试比较传统数字PGC调制解调技术和新型PGC调制解调技术的定位精度.实验过程中,传感光纤A所在温箱由-40℃升温至60℃,升温时间为1 h,而传感光纤B所在温箱温度保持25℃,在L1=0和24.52 km处进行扰动,分别测试10次.实验装置如图5所示.
2.2 实验结果及分析
实验1:两种情况下定位误差结果如图6所示.
实验2:采用新型PGC调制后的信号及采用两种PGC解调后的信号如图7~图9所示.无PGC技术、采用传统数字式PGC技术及新型PGC技术3种情况下系统的定位误差如图10所示.
从上述实验1可以看出,非互易性初始相位是M-Z分布式光纤扰动传感器的定位误差的主要因素之一,实验中温度变化的影响直接导致了非互易性初始相位的变化,其引起的最大定位误差达到2 050 m.实验2中引入了PGC调制解调技术,分别采用传统数字式PGC解调算法和新型PGC解调算法对信号进行解调,无调制解调技术时系统的最大定位误差为2 100 m,采用传统数字式PGC解调算法后系统的最大定位误差下降为700 m,采用新型PGC解调算法时系统的最大定位误差下降为100 m.从上述结果可以看出,新型PGC解调算法能够更好地恢复出原始信号,能够很好地消除非互易性初始相位造成的定位误差,提高定位精度.

图6 恒温及温度变化下定位误差分布图Fig.6 Location errors underconstant temperature and variable temperature

图8 传统PGC解调信号Fig.8 Demodulated signals by conventional PGC

图7 PGC调制信号Fig.7 Modulated signals by PGC

图10 3种情况下的定位误差分布图Fig.10 Location errors without PGC,with conventional PGC and with novel PGC

图9 新型PGC解调信号Fig.9 Demodulated signals by novel PGC
3 结 语
本文提出并实现了采用新型PGC技术的M-Z型FDDS,解决了相位漂移导致定位误差的问题.新型PGC算法适用于长距离传感系统中.采用新型PGC技术后的FDDS的定位精度由4.5 km提高到100 m.
[1] 曲志刚,靳世久,周琰.油气管道安全分布式光纤预警系统研究[J].压电与声光,2006,28(6):640-642.
Qu Zhigang,Jin Shijiu,Zhou Yan.Study on the distributed optical fiber pre-warning system for the safety of oil and gas pipeline[J].Piezoelectrics &Acoustooptics,2006,28(6):640-642.(in Chinese)
[2] 王延年,赵玉龙,蒋庄德,等.油气管线泄漏监测分布式光纤传感器的研究[J].西安交通大学学报,2003,37(9):933-936.
Wang Yannian,Zhao Yulong,Jiang Zhuangde,et al.Study on the distributed optical fiber sensor for long-distance natural gas pipeline leakage detection[J].Journal of Xi an Jiaotong University,2003,37(9):933-936.(in Chinese)
[3] Spammer S J,Swart P L,Chtcherbakov A A.Merged Sagnac-Michelson interferometer for distributed disturbance detection[J].J.Lightwave Technol.,1997,15(6):972-976.
[4] Kondrat M,Szustakowski M,Palka N,et al.A Sagnac-Michelson fibre optic interferometer:signal processing for disturbance localization[J].Opto-Electron.Rev.,2007,15(10):127-132.
[5] Chtcherbakov A A,Swart P L.Polarization effects in the Sagnac-Michelson distributed disturbance location sensor[J].J.Lightwave Technol.,1998,16(8):1404-1412.
[6] Fang X J.A variable-loop Sagnac interferometer for distributed impact sensing[J].J.Lightwave Technol.,1996,14(10):2250-2254.
[7] Rönnekleiv E.Sagnac sensor for location of a disturbance[J].Appl.Opt.1997,36(10):2076-2083.
[8] Hoffman P R,Kuzyk MG.Position determination of an acoustic burst along a Sagnac interferometer[J].J.Lightwave Technol.,2004,22(2):494-498.
[9] Kreger Stephen T.,Sang Alex K.,Gifford Dawn K.,et al.Distributed strain and temperature sensing in plastic optical fiber using Rayleigh scatter[C].Proc.of SPIE,Fiber Optic Sensors and Applications,2009,7316.
[10] Childers B A,Froggatt ME,Allison S G,et al.Use of 3000 Bragg grating strain sensors distributed on four eight-meter optical fibers during static load tests of a composite structure[C].Proc.of SPIE,2001,4332(10):133-142.
[11] Dandridge A,Tveten A B,Giallorenzi T G.Homodyne demodulation scheme for fiber optic sensors using phase generated carrier[J].IEEE Journal of Quantum Electronics,1982,Qe-18(10):1647-1653.
[12] Huang Shih-Chu,Lin Hermann Lin.Novel phase-generated carrier demodulation compensated for the propagation delay of the fiber[J].Applied Optics,2007,46(31):7594-7603.
[13] Huang Shih-Chu,Lin Wuu-Wen,Chen Mao-Hsiung.Phase sensitivity normalization in time-division multiplexing of polarization-insensitive interferometric sensors using phase-generated carrier demodulation[J].Opt.Eng.,1996,35(10):2634-2640.
[14] Xiao Hao,Li Fang,Liu Yuliang.Crosstalk analysis of a fiber laser sensor array system based on digital phase-generated carrier scheme[J].Journal of Lightwave Technology,2008,26(10):1249-1255.
[15] Dandridge A,Tveten A B,Kersey A D,et al.Multiplexing of interferometric sensors using phase carrier techniques[J].Journal of Lightwave Technology,1987,LT-5(7):947-952.

