异常高压产水气井三项式方程推导及应用
黄孝海,李晓平,袁淋
异常高压产水气井三项式方程推导及应用
黄孝海,李晓平,袁淋
(西南石油大学油气藏地质及开发工程国家重点实验室,成都610500)
异常高压气藏常具有压力高、产量大的特点,对其进行产能评价具有重要意义。一些气井在生产过程中由于工作制度不合理导致出水,使得气井的产量大幅度降低,因此准确预测异常高压产水气井产能,确定合理的工作制度显得尤为重要。在综合考虑了应力敏感、非达西流动、脉动效应及气井产水等因素的基础上,推导出异常高压产水气井的三项式产能方程;采用多元线性回归和交会法求解气井的无阻流量,并通过实例验证了其计算结果的可靠性;定量分析了渗透率敏感系数与水气质量比对气井产能的影响。计算结果表明:渗透率敏感系数对气井产能的影响要大于产水对气井产能的影响;在气藏产气量较大的情况下,脉动流对气井无阻流量的影响不可忽略。这些结论均对异常高压气藏的开采具有一定的借鉴作用。
异常高压;应力敏感;脉动效应;产水气井;三项式产能方程
0 引言
异常高压气藏中的流体在多孔介质中处于高速渗流状态,由于脉动效应的存在,使得常规的二项式不能准确地描述流体在该类气藏内的渗流问题,而必须采用Forchheimer提出的脉动效应三项式规律来描述[1-4]。在衰竭式开采过程中随着气藏压力的下降,异常高压气藏的岩石骨架承受的净上覆压力增加,使得岩石发生显著的弹塑性形变,岩石渗透率、孔隙度和岩石压缩系数等物性参数减小[5],这些参数反过来将影响孔隙流体的渗流能力。随着地层压力的下降和压降波及范围的扩大,边底水侵入,凝析水析出,气井产水量明显增大,产能相应降低[6]。异常高压气藏的开发实践和气井开发动态表明,储层的脉冲效应、介质变形和气井产水对生产的影响不容忽视,目前在预测异常高压气藏产能方程中,仅考虑了部分因素,其计算结果与实际产水气藏生产动态存在一定的差异。因此,综合考虑脉冲效应、应力敏感和气井产水等因素建立起的产能模型更接近生产实际。
1 三项式产能公式推导
1.1 产能模型的建立
异常高压下流体在多孔介质中流动的速度较大,通常利用气体在多孔介质中的三项式定律来描述气体的流动,用达西定律来描述水相的流动,即
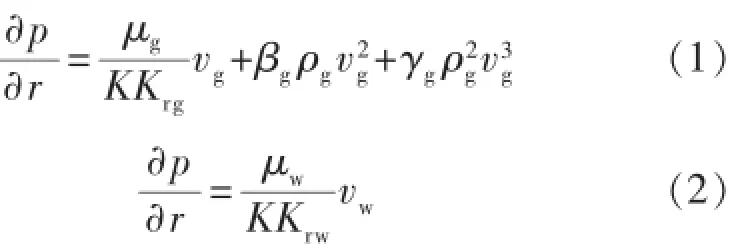
式(1)~(2)中:p为任一点的压力,Pa;r为任一点的径向距离,m;μg为天然气黏度,Pa·s;μw为水相黏度,Pa·s;K为储层绝对渗透率,m2;Krg为气相相对渗透率;Krw为水相相对渗透率;vg为气相渗流速度,m/s;vw为水相渗流速度,m/s;βg为气体紊流系数,m-1;ρg为天然气密度,kg/m3;γg为脉冲系数,m·s/kg。
在稳定渗流条件下,气水两相通过各截面的质量流量不变,其渗流速度表达式分别为

将式(3)代入式(1)和式(2),并整理得
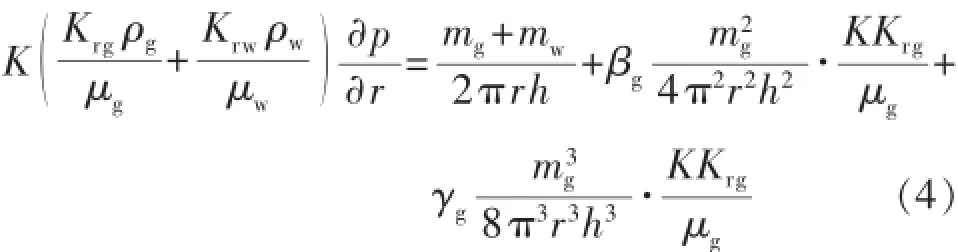
在异常高压条件下,介质发生变形,储层应力发生变化。研究表明:孔隙度随有效应力变化的幅度不明显,而渗透率随有效应力变化的幅度较为明显[7-9]。因此,笔者忽略孔隙度等的影响,仅考虑地层渗透率的变化,在公式推导过程中渗透率的变化采用指数形式[10-11]表示,即

式中:Ke为储层原始渗透率,m2;α为应力敏感指数,Pa-1;pe为原始地层压力,Pa。
速度系数的表达式为
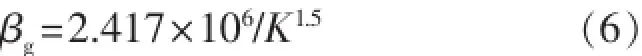
β与D的关系式[12]为
从比赛过程中获得的测试结果发现,测试球队在输掉的第二局中反映出来的参数数值非常差,而其余获胜局的测试结果数值明显较高,这也证实了排球运动中的弹跳高度与比赛结果之间强相关性的事实。测试球队运动员平均高度跳的最高的是在第一局,在第二局中有明显下降,然后仅保持在同一水平上,在第三、第四局中的表现也是明显低于第一局。

式中:γ为天然气相对密度;rwf为井筒半径,m。
将式(5)和式(7)代入式(4)得
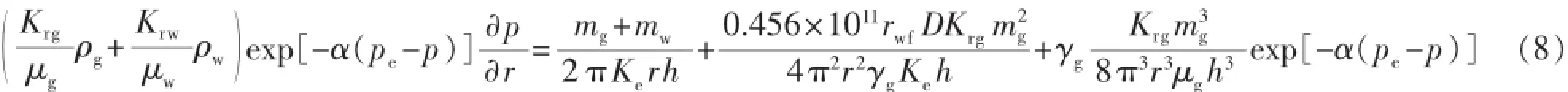
假设水气质量流量之比为Rwg=mw/mg,则气体质量流量表达式为

式中:Rwg为水气质量流量比,kg/kg;qg为气相地下体积流量,m3/s;qsc为气相地面体积流量,m3/s;ρsc为标准大气压状况下的气体密度,kg/m3。
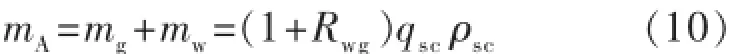
气水两相总质量流量为式中:mA为气水两相总质量流量,kg/s。
在异常高压下,考虑介质变形时气水两相的拟压力,则有

由式(8)、式(10)和式(11)得异常高压产水气井产能公式为

式中:pwf为目前井底流压,Pa;re为气藏供给的半径,m。
由式(12)得产水异常高压气藏三项式方程为


由式(13)可以看出:在异常高压条件下,气体流量和气水两相拟压力差之间不是线性关系,而是三次方关系;气体从油层边界向井底渗流过程中两相拟压力差由3部分组成;方程右边第一项用来克服气体与所产水在孔隙空间内流动的黏滞阻力;第二项用来克服流体渗流时的惯性阻力;第三项用来克服由于应力敏感所增加的渗流阻力。
1.2 三项式方程的求解
由三项式产能方程式(13)得,只要求出该式中的系数A,B和C,就可确定该井的流入动态,进而获得气井的无阻流量。求取系数A,B和C的方法较多,本文采用的是多元线性回归求取上述系数。令Δψ=ψ(pe)-ψ(pwf),则式(13)变为

此时的线性回归方程可以写成

联立上述各关系式,可以解出参数A,B和C,进而获得气井的产能方程。令pwf=0.101 MPa,此时所对应的气井产量即是无阻流量,式(13)可变为
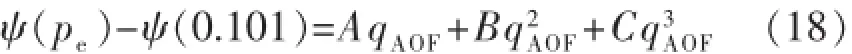
式中:qAOF为气井无阻流量,m3/s。
采用交会法求取无阻流量,对式(18)变形得

假设Y1=ψ(pe)-ψ(0.101)-BqA2OF,Y2=AqAOF+ CqA3OF,并设定一系列的qAOF值,计算出相应的函数值Y1和Y2,再以qAOF作为横坐标,Y1和Y2值作为纵坐标,得到其相交曲线,这2条曲线的交点所对应的横坐标值,即是该井的无阻流量。
2 实例分析
以国内西南部某开发井A为例:该井气藏中部深度为3 240 m,开井前测得地层静压力为43 MPa,压力系数为1.354,属于高压气藏。该井的系统试井结果如表1所列。

表1 系统试井基本数据Table 1Basic data of systematic well testing
结合气水相对渗透率曲线,对式(13)进行数值积分可以得到异常高压下气水两相拟压力的关系(图1)。
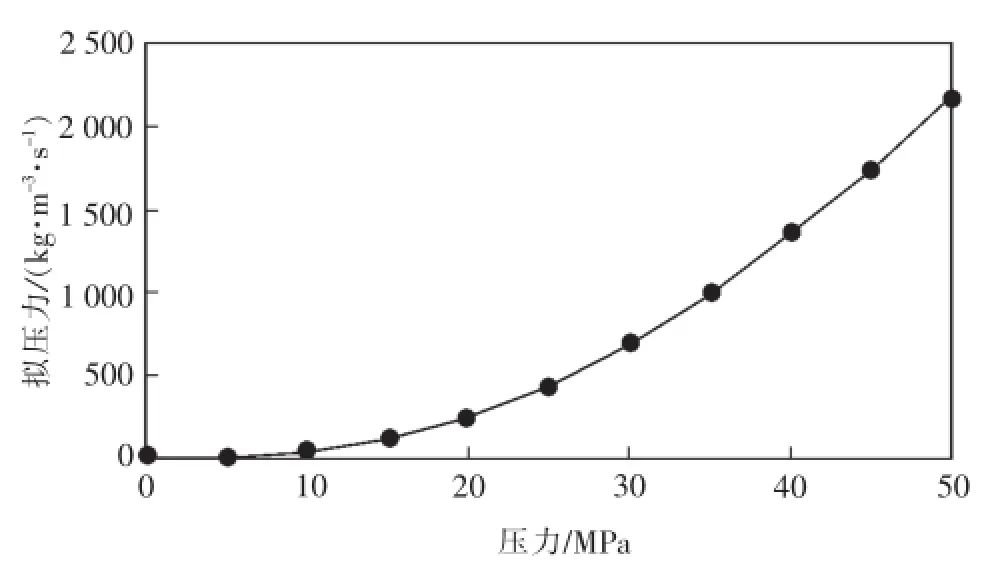
图1 气水两相拟压力关系Fig.1Relation graph of gas-water two-phase pseudopressure
采用多元线性回归[13]求取三项式产能方程中的系数分别为:A=27.48,B=0.357,C=0.016。该高压产水气井的产能方程为
ψ(pe)-ψ(pwf)=27.48qsc+0.357+0.016(20)
由式(20)第三项可知,在气井产量较高的情况下,渗流压差消耗在脉动流上所占的比例较大,因此,不能忽略脉动流对高压气井产能的影响。
令pwf=0.101 MPa,此时求得的产量即为该井的无阻流量,采用交会法[14]求取无阻流量(图2)。
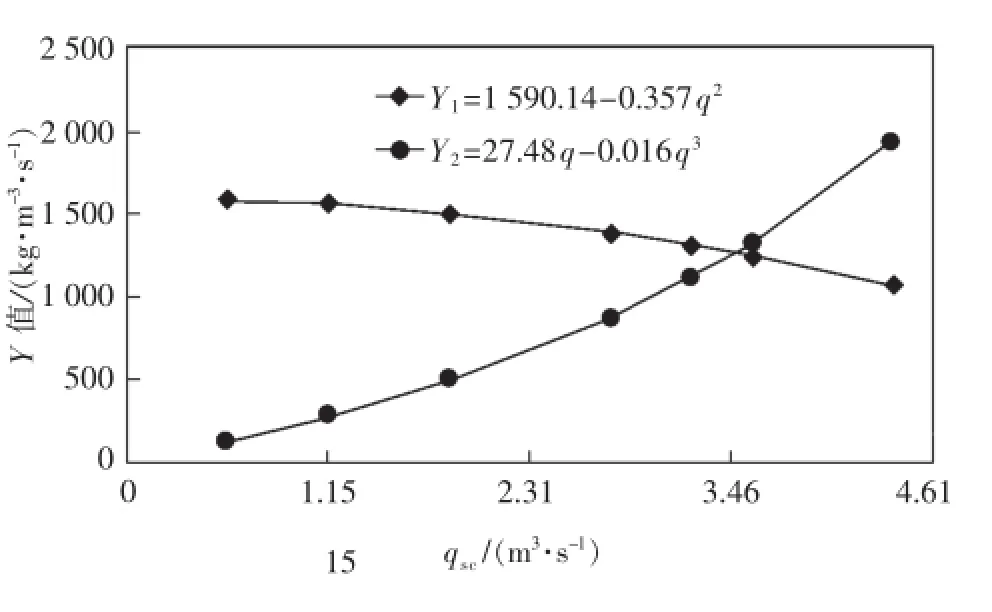
图2 交会法求无阻流量示意图Fig.2Schematic diagram of determining absolute open flow using intersection method
从图2可以看出,2条曲线的交点所对应的横坐标的大小即为该井的无阻流量:qAOF=3.49 m3/s。
如果不考虑变形介质的影响,即当渗透率敏感系数α=0时,由笔者推导的产能公式求得此时气井的无阻流量为4.12 m3/s;如果不考虑产水的影响,即地层中的流体为单相流动,采用文献[1]中的方法求得此时气井的无阻流量为3.81m3/s;如果不考虑脉动流的影响,即去除式(13)中的第三项,求得此时气井的无阻流量为4.46 m3/s。该井采用常规二项式分析方法所得无阻流量为3.58 m3/s。从计算的结果可以看出,笔者建立的产能模型获得的无阻流量最接近系统试井数据分析结果,相对误差为3%。在不考虑应力敏感、产水及脉动流对无阻流量的影响,计算所得产能相对误差分别为14.9%,6.4%,24.4%。因此,忽略这些因素的影响必将高估气井的产能。
渗透率敏感系数和水气质量比对高压气井无阻流量的影响分别如图3和图4所示:当水气质量比Rwg一定时,气井的无阻流量随着敏感系数的增大而降低,特别是敏感系数达到0.02以后,气井的无阻流量变化幅度较大;当渗透率敏感系数α一定时,气井的无阻流量随着水气质量比的增大而降低,这是由于产水量增加,地层中气水两相流动,降低了气相的相对渗透率,增加了气体流动阻力,导致气井的无阻流量大幅度降低。对比图3与图4可知,在相同条件下,渗透率敏感系数对气井产能的影响程度要大于产水对气井产能的影响。
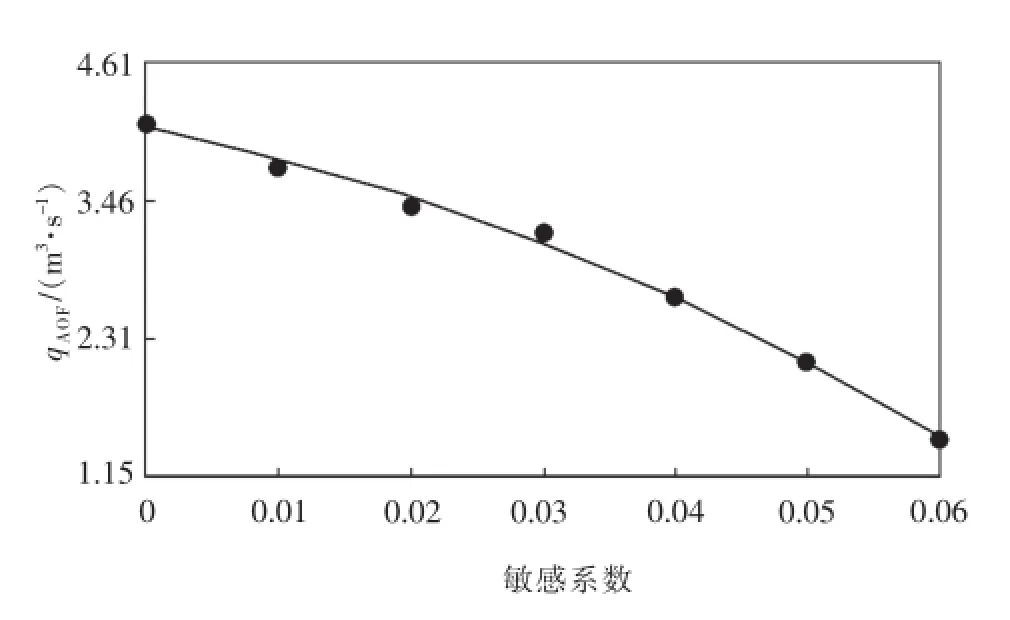
图3 渗透率敏感系数对产能的影响曲线Fig.3Influence curve of permeability sensitive coefficient on productivity

图4 水气质量流量比对产能的影响曲线Fig.4Influence curve of water-gas mass ratio on productivity
3 结论
(1)从理论上推导了异常高压产水气井的三项式产能方程,其计算结果精度较高,具有较强的实用性。
(2)在高压气井中,如果产气量较大,脉动流对气井无阻流量的影响不可忽略。
(3)同等条件下,渗透率敏感系数对气井产能的影响要大于产水对气井产能的影响。
[1]葛家理.油气层渗流力学[M].北京:石油工业出版社,1982:18-140.
[2]陈元千.油气藏工程计算方法[M].北京:石油工业出版社,1989:83-126.
[3]林平一.油藏工程[M].北京:石油工业出版社,1999:36-224.
[4]刘荣和,郭春华,冯文光,等.低渗透气藏压裂井三项式方程推导及应用[J].天然气工业,2006,26(9):109-111.
[5]张风波.异常高压气藏动态分析方法研究[D].成都:西南石油大学,2008.
[6]文华,刘义坤,孙娜.基于广义拟压力法的深层火山岩产水气井产能方程[J].大庆石油学院院报,2010,34(1):43-46.
[7]代平.低渗透应力敏感油藏实验及数值模拟研究[D].成都:西南石油大学,2006.
[8]黄继新,彭仕宓,黄述旺,等.异常高压气藏储层参数应力敏感性研究[J].沉积学报,2005,23(4):620-625.
[9]朱中谦,王振彪,李汝勇,等.异常高压气藏岩石变形特征及其对开发的影响——以克拉2气田为例[J].天然气地球科学,2003,14(1):60-64.
[10]巢华庆,王玉普.复杂油藏试井技术[M].北京:石油工业出版社,2002:21-25.
[11]李传亮.岩石应力敏感指数与压缩系数之间的关系式[J].岩性油气藏,2007,19(4):95-98.
[12]郭煜锴,刘德华,赵楠,等.水平气井流入动态计算新方法研究[J].石油天然气学报,2009,31(1):118-120.
[13]罗银富,黄炳光,王怒涛,等.异常高压气藏气井三项式产能方程[J].天然气工业,2008,28(12):81-82.
[14]陈春燕.异常高压气藏气井产能方程求解的简易方法[J].天然气工业,2007,27(4):88-89.
(本文编辑:杨琦)
Deduction and application of trinomial equation for water producing gas well with abnormal pressure
HUANG Xiaohai,LI Xiaoping,YUAN Lin
(State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China)
The gas reservoir with abnormal pressure is characterized by high pressure and large productivity,so,it is very important to evaluate the deliverability.Meanwhile,the water breakthrough often occurs in the gas well under certain unreasonable working systems,which reduces the productivity significantly.Thus,it is vital to confirm the reasonable working system on the base of accurate prediction of the productivity of gas well with abnormal pressure. Considering stress sensitivity,non-Darcy flow,pulsation effect and water producing of gas well,this paper deduced a trinomial equation for water producing gas well with abnormal pressure.On the basic of the multiple linear regression and intersection method,absolute open flow capacity was determined and the correctness of result was demonstrated by the case analysis.The effects of permeability sensitivity coefficient and water/gas mass ratio on the gas well productivity were quantitatively analyzed.Calculation results show that∶the effect of permeability sensitivity coefficient on gas well productivity is greater than that of producing water;for the gas well with large productivity,the effect of pulsating flow on the absolute open flow of gas well should not be overlooked.This study has significance for the exploitation of abnormal pressure reservoir.
abnormal pressure;stress sensitivity;pulsation effect;water producingofgas well;trinomial deliverability equation
TE37
:A
2013-12-20;
2014-04-20
国家杰出青年科学
“油气渗流力学”(编号∶51125019)资助
黄孝海(1987-),男,西南石油大学在读硕士研究生,研究方向为油气藏工程及油气渗流。地址:(610500)四川省成都市西南石油大学油气藏地质及开发工程国家重点实验室B403。E-mail:yingyunhxh@163.com。
1673-8926(2014)05-0119-05

