边水推进对水平井产量的影响

李晓平，袁淋，罗诚，刘斌，刘振平

边水推进对水平井产量的影响

李晓平1，袁淋1，罗诚2，刘斌1，刘振平1

（1.西南石油大学油气藏地质及开发工程国家重点实验室，成都610500；2.中国石油川庆钻探工程公司地质勘探开发研究院，成都610056）

边水油藏开发过程中，即使水平井井底未见水，但边水推进仍会影响水平井产量。基于水平井三维渗流场模型，将三维渗流场分为内部和外部2个径向渗流场，考虑外部渗流场边水推进的影响，分别运用坐标变换与保角变换方法求得内部与外部渗流场的产能公式，根据等效渗流阻力原理最终获得了考虑边水推进的水平井产能计算新公式。实例计算发现，新公式计算结果与实际产量绝对误差及相对误差均较小，表明新公式准确性较高，实用性较好。敏感性分析结果表明，考虑边水推进条件的水平井产量小于未考虑边水推进条件的水平井产量，且随着边水推进距离增大，水平段长度越小，产量减小的幅度越大；水平段长度越大，产量减小的幅度越小。该研究成果为边水推进过程中水平井产能预测提供了新思路。

边水推进；椭圆形；坐标变换；保角变换；水平井产量

0 引言

水平井技术已在边水油藏开发中广泛运用［1-3］，这是因为水平井具有泄油面积大和生产压差小等特点，但是边水推进以及由此导致的井底见水均是影响水平井产量的重要因素。目前，虽然国内外学者［4-7］提出了一系列优化方法，通过控制水平井井筒位置以及产量来延缓井底见水的时间，但是始终无法避免边水推进，最终导致产量下降。目前的边水油藏水平井稳态产能公式只适用于边水推进前水平井产能的预测［8-9］，而关于边水推进过程中水平井产能预测模型尚未见报道。笔者以Joshi［10］对水平井产能的研究为基础，将水平井三维渗流场分为内部与外部2个径向渗流场，考虑外部渗流场边水推进的影响，分别运用坐标变换与保角变换方法得到边水推进过程中水平井产能计算新公式；同时利用实例数据验证新产能公式的准确性，并分析边水推进对水平井产能的影响，为边水油藏开发过程中水平井产能预测提供新思路。

1 产能公式推导

1.1 物理模型

假设水平井位于顶、底封闭和水平方向存在边水供给边界的各向异性油藏中部，流体在油藏中的渗流为稳定渗流，流体微可压缩，不考虑表皮效应以及井筒压降对水平井产能的影响，边水沿水平方向呈椭圆形径向推进，边水推进区域内为油水两相渗流，目前井底尚未见水。水平井内部渗流场与外部渗流场的物理模型如图1所示。图1中a1，a2与a3分别为椭圆形供给边界、油水前缘及内部渗流场的长半轴，m；b1，b2与b3分别为椭圆形供给边界、油水前缘及内部渗流场的短半轴，m；pe1，pe2，pe3与pwf分别为油藏边界驱动压力、油水前缘处压力、内外部渗流场交界面压力以及目前井底流压，MPa；h为油层厚度，m；d为目前边水推进距离，m。

1.2 内部渗流场产能公式推导

内部渗流场等压线为一簇簇椭球面［11］，当压力波呈椭球面传播到油藏顶、底边界时，椭球面为内部渗流场的供给边界［参见图1（a）］，该椭球面方程可以写为

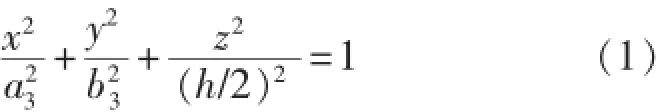
在椭球面供给边界上任一位置χ处的y-z横截面均为一个椭圆，椭圆方程及长、短半轴分别为

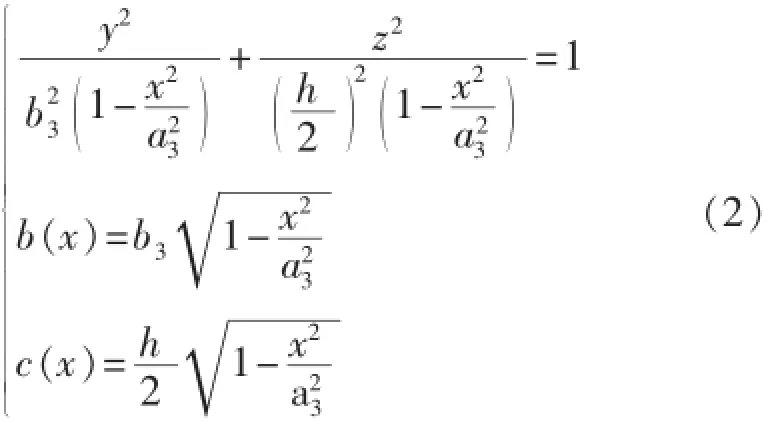
图1 水平井内部与外部渗流场物理模型Fig.1Physic models of internal seepage field and external seepage field of horizontal well

在水平井任一位置χ处选取微元井段dχ，其在y-z平面内可以看成椭圆形供给边界中的一口“普通直井”［图2（a）］，其中Kv和Kh分别为油藏垂直方向和水平方向渗透率，mD。假设各向异性地层中渗透率张量方向与坐标轴方向相同，则y-z平面上稳态渗流方程为

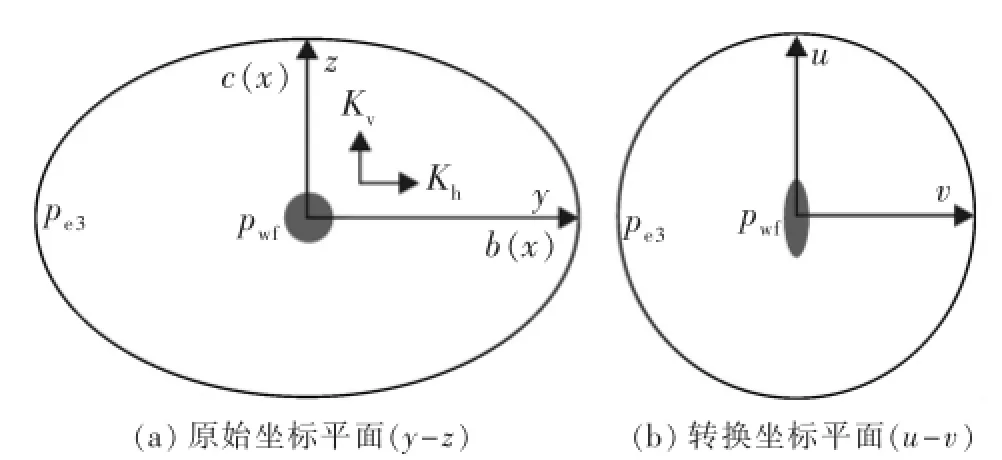
图2内部渗流场坐标变换Fig.2Coordinate transformation in internal seepage field

式中：p为内部渗流场任一位置处的压力，MPa。

内部渗流场边界条件为

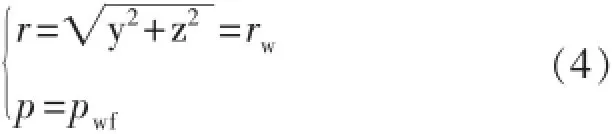
式中：r为内部渗流场任一点的径向距离，m；rw为井筒半径，m。

可转变为拉普拉斯方程，即

内部渗流场边界条件变为

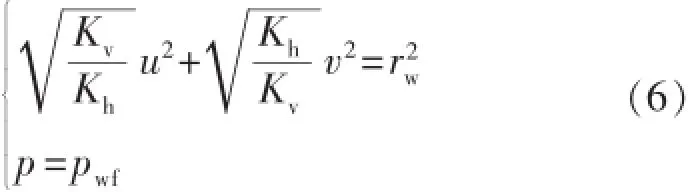
引入保角变换u=mcoshρcosθ和v=msinhρsinθ，将椭圆坐标系转变为ρ-θ极坐标系，其中m为待定常数，设ρw代表井筒椭圆参数，应用cos2θ+sin2θ=1，式（7）可变为

内部渗流场边界条件变为ρ=ρw和p=pwf，由于式（7）的解与θ无关，因此式（7）的解为p=pwf+C（ρρw），其中C为与流量有关的常数。沿着闭合等压线对速度进行积分可以得到流量dqo，即

式中：dqo为微元段产量，m3/d；vn为等压线法线方向渗流速度，m/d；s为等压线圆弧，m。

对式（8）进行积分，结合内部渗流场边界条件得

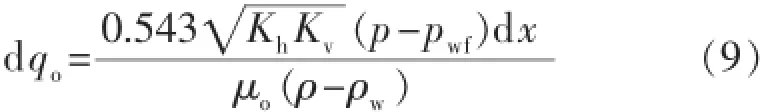
式中：μo为原油黏度，mPa·s；ρw为极坐标系中的井筒半径，m。

当ρ取较大值时，cosh ρ≈sinh ρ，u-v平面上等压线为圆形［参见图2（b）］。等压线平均半径可以定义为内部渗流场椭圆长轴与短轴的平均值，即式中：为内部渗流场任一点处的长、短半轴平均值，mw为井筒半径的平均值，m。

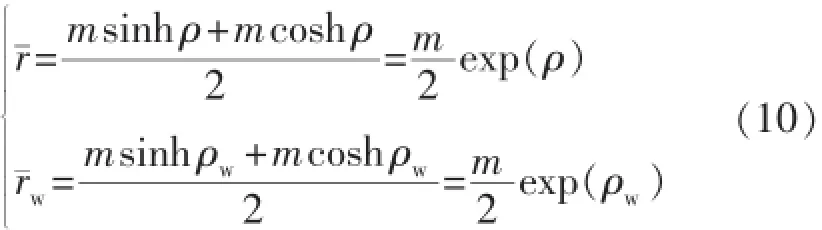
将式（10）代入式（9）得

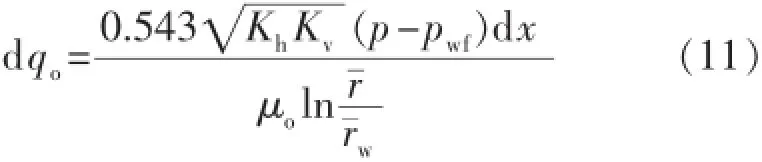
式中：β为各向异性系数，无量纲。

在内部渗流场供给边界上，选取点（ve，0），由式（10）得

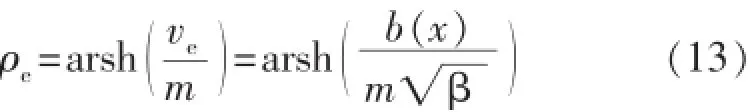
式中：ρe为极坐标系中的内部渗流场供给半径，m；ve为坐标变换后内部渗流场供给边界上一点，m。

由式（10）及式（13）可得到内部渗流场平均供给半径，即

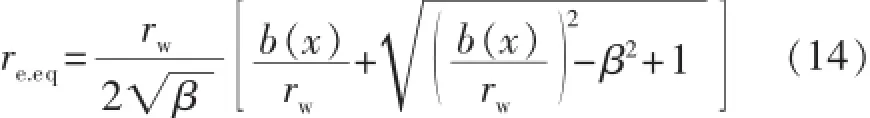
式中：re.eq为内部渗流场平均供给半径，m。

因此，式（11）可变为

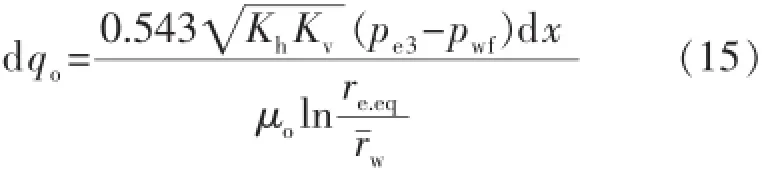
通常情况下，油层厚度等于水平井水平段长度的直井的产量计算公式为

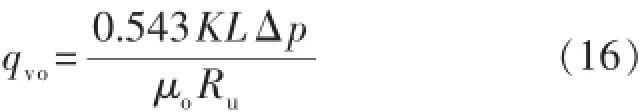
式中：K为直井地层渗透率，mD；L为水平井水平段长度，m；Δp为直井生产压差，MPa；qvo为直井产量，m3/d；Ru为内部渗流场等效阻力，无量纲。

对比式（15）与式（16），并对χ在［-L/2，L/2］进行积分，得到内部渗流场的等效阻力为

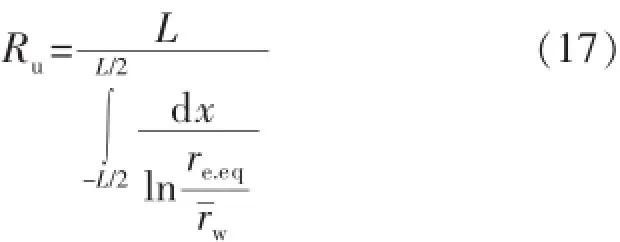
1.3 外部渗流场产能公式推导

随着边水的推进，外部渗流场变为椭圆形复合区域，引入保角变换［12］，即

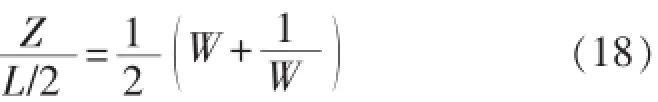
式中：Z与W分别为保角变换前、后外部渗流场任一点处的坐标，C。

通过保角变换，将椭圆形复合区域内的渗流问题变换为圆形复合区域的渗流问题（图3），图3中Re1，Re2和Re3分别为保角变换后的供给边界、油水前缘和外部渗流场等效井筒直径，m。

变换后圆形复合区域的半径分别为

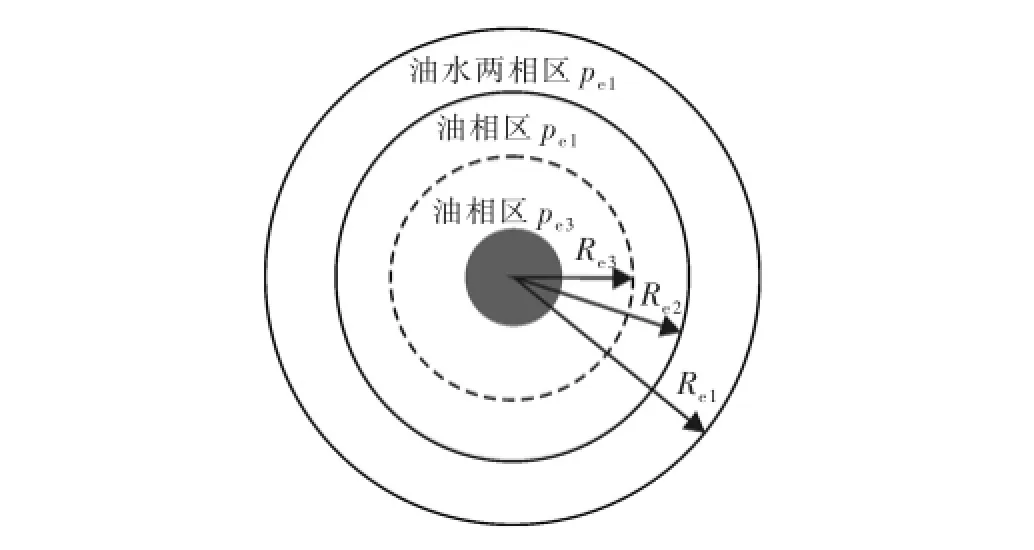
图3 外部渗流场保角变换的圆形复合区域Fig.3Circular composite area after conformaltransformation in external seepage field

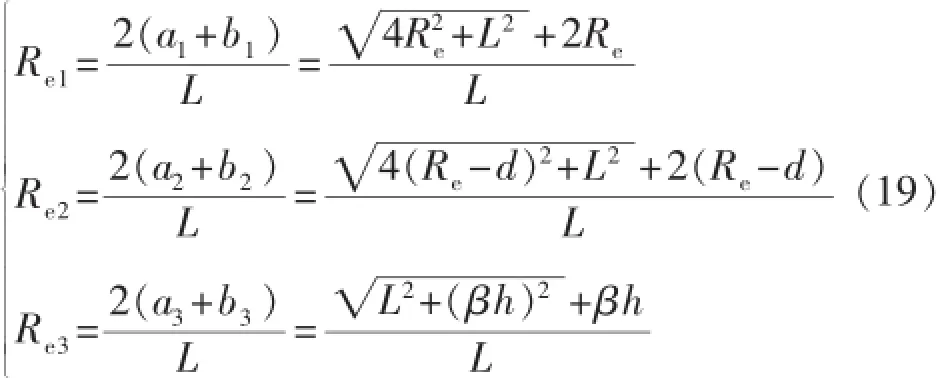
式中：Re为保角变换前的供给边界，m。

在Re3—Re2区域内，流体为油相单相渗流，根据平面径向单相渗流，可得

式中：qo为水平井地下流量，m3/d。

在Re2—Re1区域内，流体为油水两相渗流，根据平面径向两相渗流原理，可得

式中：qL为外部渗流场地下产液量，m3/d；Krw为水相相对渗透率，无量纲；Kro为油相相对渗透率，无量纲；μw为水相黏度，mPa·s。

含水饱和度分布规律满足径向Buckley-Levereet方程［13］：

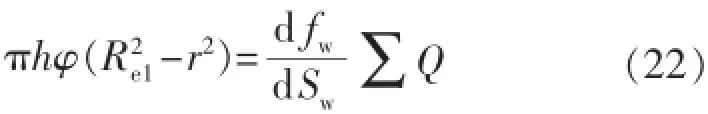
式中：φ为储层孔隙度，%；fw为分流率，无量纲；Sw为含水饱和度，%；Q为边水累计推进量，m3。

当r=Re2，则该处为油水驱替前缘，则式（22）可以写为

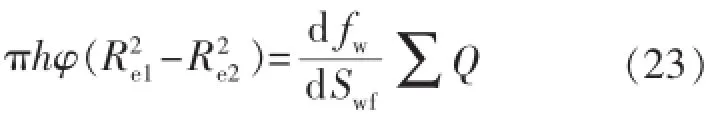
式中：Swf为前缘含水饱和度，%。

综合式（22）～（23），可得

式中：Sw为含水饱和度，%。

对式（24）两边同时微分，得

将式（25）代入式（21），并利用分流率的表达式［14］，油水两相区等效渗流阻力为

1.4产能公式

根据油藏体积守恒原理qo=qL，结合内部与外部渗流场产能公式，得到考虑边水推进条件的水平井产能公式，即

式中：qosc为水平井地面产量，m3/d。

A1的求解方法有2种：一种是图形拟合法，另一种是数值积分方法。由于求解A1的已知数据均为离散分布，图形拟合法容易产生较大的误差，因此，笔者利用数值积分方法求解，具体步骤为：①根据岩心测试数据作油水两相相对渗透率曲线，再根据分流率表达式计算并绘制分流率分布曲线，求取分流率导数，得到前缘含水饱和度以及前缘含水饱和度对应的分流率导数；②利用各离散数据计算A1，A2与A3，将［0，fw′（Swf）］分为若干个微元段，在每个微元段内运用梯形公式可计算分流率导数的积分值，则整个区间内的积分值为各个微元段积分值的和。

2 实例计算及影响因素分析

某边水油藏中水平井基本参数为：油层厚度为10 m，油藏水平方向和垂直方向渗透率分别为3 mD和0.5 mD，边水驱动压力为30 MPa，驱动半径为300 m，水平段长度为500 m，井筒半径为0.1 m，井底流压为17 MPa，原油黏度为1 mPa·s，地层水黏度为0.6 mPa·s，原油体积系数为1.2 m3/m3，初投产产量为10.66 m3/d，目前边水推进距离为20 m，产量为10.53 m3/d，其油水两相相渗曲线及分流率曲线如图4所示。

利用实例参数、相对渗透率及分流率数据求得A1，A2与A3，并将其代入式（27），计算得到边水推进条件下（d=20 m）水平井产量为10.34 m3/d。该计算结果与实际产量数据绝对误差为0.19 m3/d，相对误差为1.80%，绝对误差与相对误差均较小，表明该产能新公式准确性较高，实用性较强。

图4 相对渗透率曲线（a）与分流率曲线（b）Fig.4Curves of relative permeability（a）and shunt index（b）

在实例数据的基础上，制作考虑边水推进条件（d≠0）与不考虑边水推进条件（d=0）的边水驱油藏水平井产量随水平段长度变化的关系曲线（图5）。

图5 边水推进对水平井产量的影响Fig.5Effect of edge water incursion on productivity of horizontal well

从图5可以看出，随着水平段长度增加，水平井产量逐渐增大，但是增大趋势越来越平缓。对于任意水平段长度，考虑边水推进条件下的水平井产量比不考虑边水推进条件的水平井产量低，这是因为边水推进使得外部渗流场由油相单相渗流变为局部油水两相渗流，增大了渗流阻力，因而产量降低，水平段长度越小时产量降低越明显。

将其他参数固定，制作不同边水推进距离条件下水平井产量随水平段长度变化的关系曲线（图6）。从图6可以看出，边水推进并未改变水平井产量随水平段长度变化的趋势，产量仍随水平段长度的增大而增大，但是增大趋势越来越平缓。当水平段长度一定时，随着边水推进距离增大，水平段产量逐渐减小，特别是水平段长度较小时，产量减小更加明显，而当水平段长度较大时，边水推进距离对水平井产量的影响较小。这是因为随着边水推进距离增大，外部渗流场的两相渗流区越来越大，渗流阻力也逐渐增大，因此使得产量减小。对于水平段长度较小的水平井，其对应的泄油面积相对较小，因而两相渗流区域占总泄油面积的比值将更大，随着边水推进距离增大，渗流阻力增加的速度将更快，因而产量减小更明显，反之越不明显。

图6 不同边水推进距离对水平井产量的影响Fig.6Effect of different distance of edge water incursion on productivity of horizontal well

3 结论

（1）在边水油藏开发过程中，井底虽未见水，但边水推进后，外部渗流场局部区域变为油水两相渗流，内部渗流场仍为椭圆形油相单相径流，总的渗流阻力增大，因此油井产量会降低。

（2）利用坐标变换与保角变换方法推导了考虑边水推进过程中产量计算新公式。实例计算发现，利用新公式计算的结果与实际产量的绝对误差和相对误差均较小，说明新公式准确性较高。

（3）敏感性分析表明，不考虑边水推进条件的水平井产量高于考虑边水推进条件的水平井产量，且随着边水推进距离增大，产量逐渐减小。对于水平段长度较小的水平井，边水推进距离对其产量的影响较明显，而对于水平段长度较大的水平井，边水推进距离对其产量影响较小。

［1］Barge D，Al-Shaarawy O，Jha M，et al.Successful use of horizontal well technology in mitigating water production and increasing oil recovery in the South Umm Gudair Field，PNZ，Kuwait［R］.SPE 93379，2005：1-9.

［2］周春香，李乐忠，王敏.西58-8小断块边水油藏天然能量评价研究［J］.岩性油气藏，2009，21（4）：111-114.

［3］饶良玉，吴向红，李贤兵，等.苏丹层状边水油藏水平井开发效果评价与对策研究［J］.岩性油气藏，2011，23（5）：106-110.

［4］张勇，沈燕来，杨寨.边水驱油藏水平井合理位置的确定方法研究［J］.西南石油学院学报，2003，25（5）：43-45.

［5］田风民.水平井的优化设计及油藏潜力挖掘研究［J］.渤海大学学报：自然科学版，2007，28（3）：207-211.

［6］HernandezJC，WojtanowiczAK.Optimum well completion strategies in reservoirs with bottom and edge water invasion［C］.Canadian International Petroleum Conference，Calgary，Alberta，2007：1-13.

［7］Thornton K，Silliman M Y，Jorquera R，et al.Optimization of inflow control device placement and mechanical conformance decisions using a new coupled well-intervention simulator［R］.SPE 139435，2010：1-10.

［8］范子菲，林志芳.边水驱油藏水平井产能公式研究［J］.大庆石油地质与开发，1994，13（2）：33-37.

［9］郭宝玺，王晓东，罗万静，等.边水油藏水平井三维产能计算新方法［J］.现代地质，2007，21（1）：141-144.

［10］Joshi S D.Augmentation of well productivity with slant and horizontal wells［R］.SPE 15375，1988：729-739.

［11］袁淋，李晓平，孙飞，等.基于相似流动替换法预测水平井产量［J］.油气地质与采收率，2013，20（6）：87-90.

［12］袁淋，李晓平，张璐，等.水平井稳态产能公式对比与分析［J］.岩性油气藏，2013，25（6）：127-132.

［13］计秉玉.油水两相径向稳定渗流条件下压力分布及产量变化特征［J］.大庆石油地质与开发，1995，14（3）：44-46.

［14］李晓平.地下油气渗流力学［M］.北京：石油工业出版社，2008：128-133.

（本文编辑：李在光）

Effect of edge water incursion on productivity of horizontal well

LI Xiaoping1，YUAN Lin1，LUO Cheng2，LIU Bin1，LIU Zhenping1
（1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation，Southwest Petroleum University，Chengdu 610500，China；2.Geological Exploration and Development Research Institute，CNPC Chuanqing Drilling Engineering Co.Ltd.，Chengdu 610056，China）

During the development of reservoir with edge water,even if the water didn’t break through at the bottom of the horizontal well,the edge water incursion still influences the productivity of horizontal well.Based on the threedimensional seepage field model of horizontal well,this paper divided the three-dimensional seepage field into two two-dimensional seepage field which are called internal seepage field and external seepage field respectively,used the methods of transformation of coordinates and conformal mapping to obtain the productivity formulas of the two two-dimensional seepage field,eventually got the new productivity formula of horizontal well considering the edge water incursion according to the principle of equivalent filtration resistance.Practical example shows that result calculated by new formula has small absolute and relative error with actual output,which indicates that the new formula is of high accuracy and good practicability.Sensitivity analysis demonstrates that productivity of horizontal well in consideration of edge water incursion is lower than that with no consideration of edge water incursion. Meanwhile,as the increasing of edge water incursion distance,the productivity of horizontal well decreased to a great extent with short horizontal section,while if the horizontal well length is long enough,the effect can be neglected. This study can provide a new solution to predict the productivity of horizontal wells during edge water incursion.

edgewaterincursion；ellipse；coordinatetransformation；conformalmapping；productivityofhorizontalwell

TE32+8

：A

2013-11-29；

2014-02-18

国家杰出青年科学基金“油气渗流力学”（编号：51125019）与教育部“长江学者和创新团队发展计划”（编号：IRT1079）联合资助

李晓平（1963-），男，博士，教授，博士生导师，主要从事渗流力学、试井分析及油气藏工程方面的教学和科研工作。地址：（610500）四川省成都市新都区西南石油大学油气藏地质及开发工程国家重点实验室B403室。E-mail：nclxphm@126.com。

1673-8926（2014）05-0107-06