OFDM系统中基于非统计信息的信道估计优化算法研究*

周 冰,杨建平

(中国电子科技集团公司第30研究所,四川成都610041)

OFDM系统中基于非统计信息的信道估计优化算法研究*

周 冰,杨建平

(中国电子科技集团公司第30研究所,四川成都610041)

传统的信道估计算法优化是采用MMSE及其变形LMMSE等一类算法,但该算法需要大量的信道统计信息,复杂度高,文中的信道估计方法采用基于导频的信道方法,该方法通过把信道冲激响应中最有利用价值的采样点抽取出来,去除掉噪声的干扰。使得性能能达到MMSE(最小均方误差)信道估计算法的性能。又尽量避免利用传统MMSE等一类算法中计算大量的信道先验统计信息。降低算法的复杂度,利于工程实现。文中论述了两种算法,门限选择算法和即时能量算法。通过仿真验证,这两种算法都基本接近MMSE算法的性能,但运算量大大减少,在实际工程实现中极具实用价值。

正交频分多址 信道估计 最小均方误差 非统计信息

0 引 言

OFDM由于采用低复杂度的信道估计均衡器处理频率选择性衰落,在军用及民用无线通信领域广泛应用[1]。显然如果能够正确估计信道冲激响应(CIR),均衡器才能发挥作用。即信道估计已成为决定接收机接收性能的重要部分。通常情况下, OFDM采用导频辅助(即导频)的方式进行信道估计,由于插值或滤波的不同,算法也有很多种。以最小均方误差(MMSE)为准则的二维时频维纳滤波算法[2]性能优异,但是该算法必须知道信道统计信息,算法复杂度过高。在文献[3]中,通过在时间和频率上分别做一维滤波降低复杂度,但是仍需要导频子载波上信道的自相关信息,计算中涉及复杂的矩阵求逆和相乘,仍具有较高的实现复杂度。在文献[4-5]中,通过简化信道自相关矩阵的方式来减少运算量,但该方法的运算量仍不可轻视。基于DFT的算法,不需要统计信息,运算量较小,但是性能也比较中庸[6]。很多研究工作都致力于在不提高算法复杂度的情况下去提升算法的性能[7]。

提升算法性能主要思想是,在经过IDFT变换后,不是所有的信道冲激响应值都是有意义的,其中有些是噪声引起的。如果有方法能够精简信道冲激响应,只留下有用的信道冲激响应值,性能就可以在不提高复杂度的前提下得到提升。出于这个目的,文献[8]中提出只选择J个能量最强的信道冲激响应值,很明显J是一个很重要的设计参数,当J等于非零的信道阶数(Nt)时,算法性能非常好,但是当J与Nt不相等时,性能迅速恶化。

本文的目的主要有以下两点。第一,提出了两种方法:门限选择算法(TCS)和即时能量算法(IES)来选择最优的冲激响应集。选择的数目可以根据算法动态调整。两种方法都得到了MSE(最小均方误差),其值很接近MMSE信道估计的性能,尤其是在导频数远大于信道冲激响应非零值的数目时。该方法只需要知道信噪比值,不需知道复杂的信道自相关信息,从而使运算量急剧减小。第二,通过仿真验证了算法性能,同时给出在信道模型下的误码率测试结果。

1 系统模型

假定OFDM符号使用N个子载波,每个子载波包括数据符号X[k],k表示子载波序号。时域的OFDM发射信号可以表示为:

n表示OFDM信号时域样点序号。

在添加CP后,将此信号通过多径信道,可表示为:

y[n]=x[n]⊗h[n]+w[n],0≤n≤N-1(2)⊗表示循环卷积,w[n]是具有零均值,方差为= E[|w[n]|2]的独立同分布的高斯白噪声。h[n]为离散时间冲击响应,,其中al表示不同的路径复增益,l表示不同路径延迟的序号。

第k个子载波频域的表达式为:

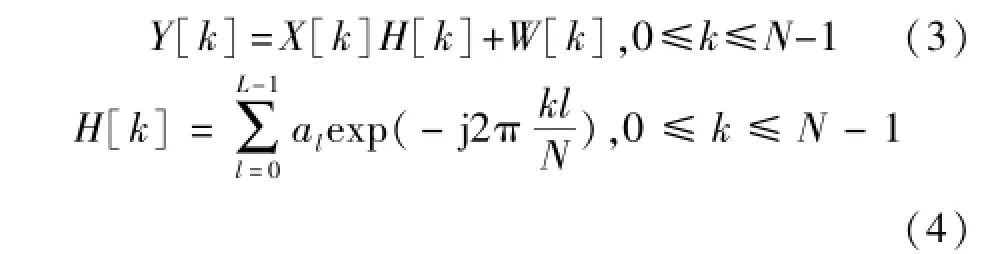
假定导频均匀分布在OFDM符号上(疏状导频,等间距),假定导频位于第k个子载波上,首先使用LS估计,其频响可表示为:P表示所有导频所在的子载波集合。

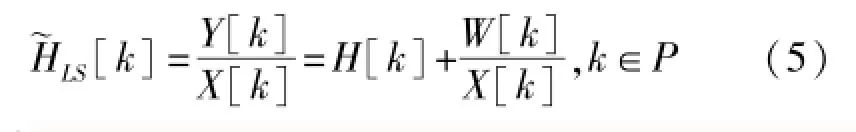
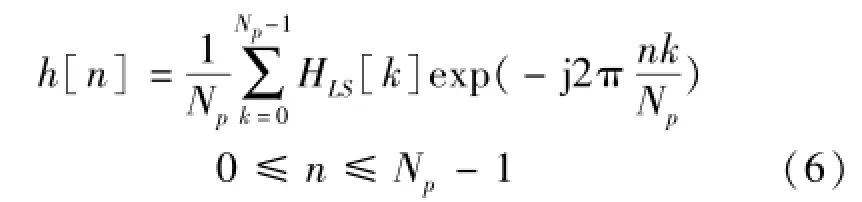
对在导频位置上得到的信道估计值进行IDFT变换,进而估计出时域上的CIR,Np表示所有导频的集合。假定Np＞L,整个频域上的CTF(信道传输函数)估计可以通过在整个OFDM符号周期补零得到[9]:

2 信道估计优化算法描述

IDFT之后的信道冲激响应并不是所有的值都是有意义的,有些非零的冲激响应值可能是由于噪声引起的,在该位置处本身并不存在信道冲激响应值。特别是在信道冲激响应的阶数比较稀疏时,去掉一些没有意义的冲激响应,会减小噪声的影响。

全球移动通信协会（GSMA）首席执行官洪曜庄看到，在新技术的浪潮中，传统媒体转型势在必行。未来的数字世界，移动设备将会是数字变革中的核心，传统媒体要做好快速迁移的准备。没有一成不变的格局，也没有一劳永逸的创新。在这个“新”与“旧”快速更迭的时代，谁会是下一个领跑者，是一个待解的谜题。拥抱变化、随时出发，是人们给出的题解，当然，也有人在用想象让人们走在时间之前，感触未来。

图1 OFDM系统信道估计处理框Fig.1 Channel estimation processing diagram

图1给出了信道估计处理的主要过程,本节所描述的部分就是算法处理部分(TCS和IES)

2.1 门限选择算法(TCS)

即时门限选择算法以最小均方误差准则为依据,式(8)～式(16)给出一些定义:

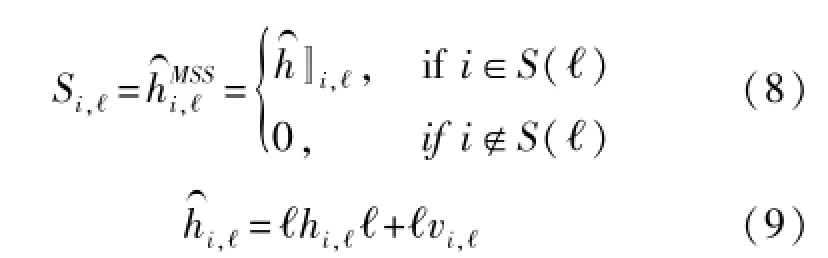
S(ℓ)代表第ℓ个符号的信道冲激响应的优化集,为信道冲激响应估计值,hi,ℓℓ为理论值,vi,ℓ为噪声分量。hi,ℓ和vi,ℓ分别服从如下分布(10)(11),ρ代表导频信噪比,Np为导频数目,Nc表示正态分布。C表示理论信道冲激响应中不为0的集合。

则信道冲激响的优化集(估计值)与理想值之的差值如下定义:

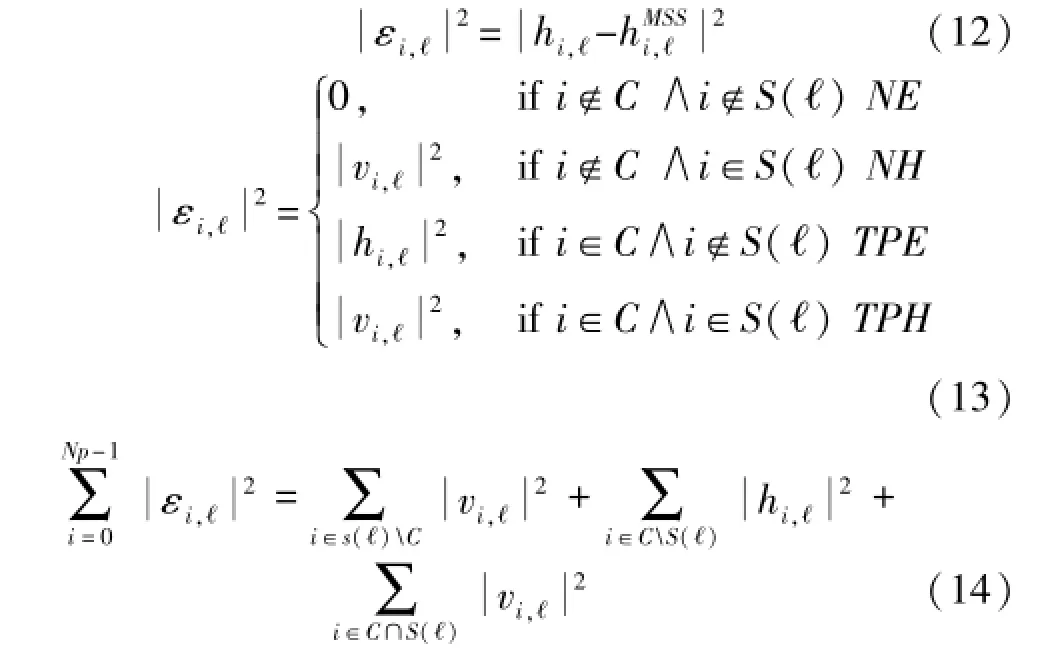
NE表示该冲激响应为噪,既不在理论冲激响应集中也不在最优冲激响应集中,被排除在外,对误差不产生影响。NH表示是噪声,但被错认为属于优化集。TPE表示该冲激响应被排除在优化集之外,但是它原是信道冲激响应的理论值,它产生的误差如上式。TPH表示该冲激响应值属于理论冲激响应,并且在优化集之内。

下式为TCS算法优选集的定义,ζ为门限值,

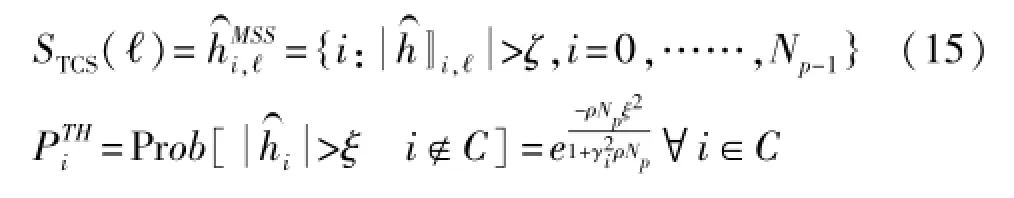
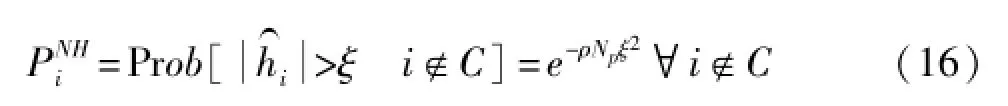
TCS算法的均方误差如式(17)所示。

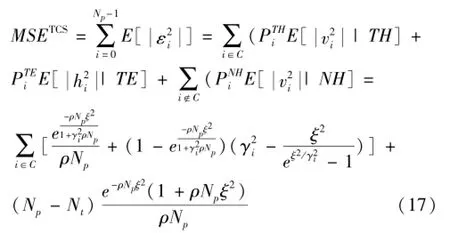
目标是使其MSE最小

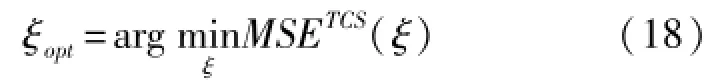
求最小值,使式(17)一阶导数为0,假设条件Nt+ρNp≈ρNpρNp＞＞NtρNpξ2＞＞1成立,则门限取值如式(19)所示。

2.2 即时能量选择算法(IES)

主要思想是通过有序的选择最强的CIR(信道冲击响应)估计样点,使得总能量达到接收能量的估计值。首先,将估计的CIR估计样点按照绝对值大小进行排列:

门限T表示总接收能量的估计值:

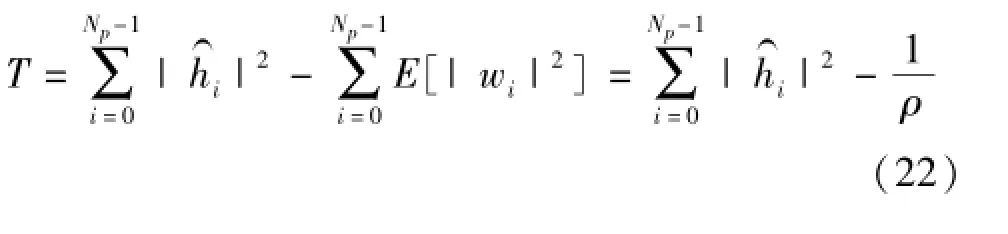
3 算法仿真验证

首先,在等功率静态多径模型下验证不同方法的信道估计的MSE(均方误差)性能,从而验证了本文提出的方法确实对基于导频辅助信息的信道估计算法的性能提升作用明显。然后以门限选择算法(TCS)方法为例,给出其在信道模型下的误比特性能。仿真参数如表1所示。

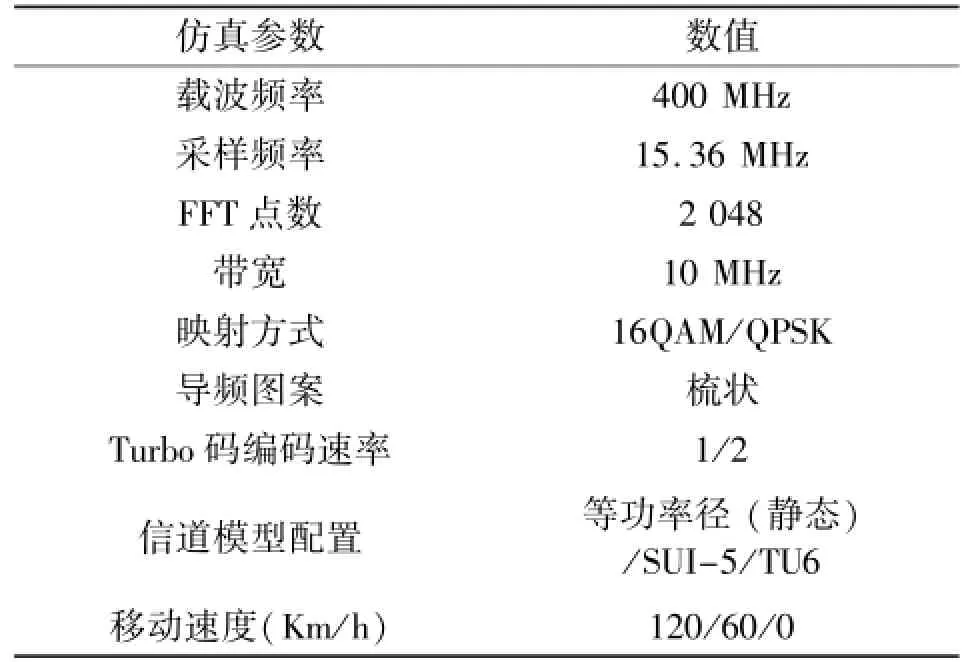
表1 仿真参数设置Table 1 Simulation parameter settings

多径信道模型采用TU及SUI的典型信道模型,TU信道模型是3GPP定义的经典数字移动通信信道模型,它定义了城市环境中没有直视径的情况,多径能量服从瑞利分布。SUI是斯坦弗大学根据对山地信道进行测量后得到的统计模型,它针对的是有直视径的情况,所以多径能量服从莱斯分布。SUI5信道模型代表的是树林覆盖的山地模型(较好情况)。多径参数如表2所示。

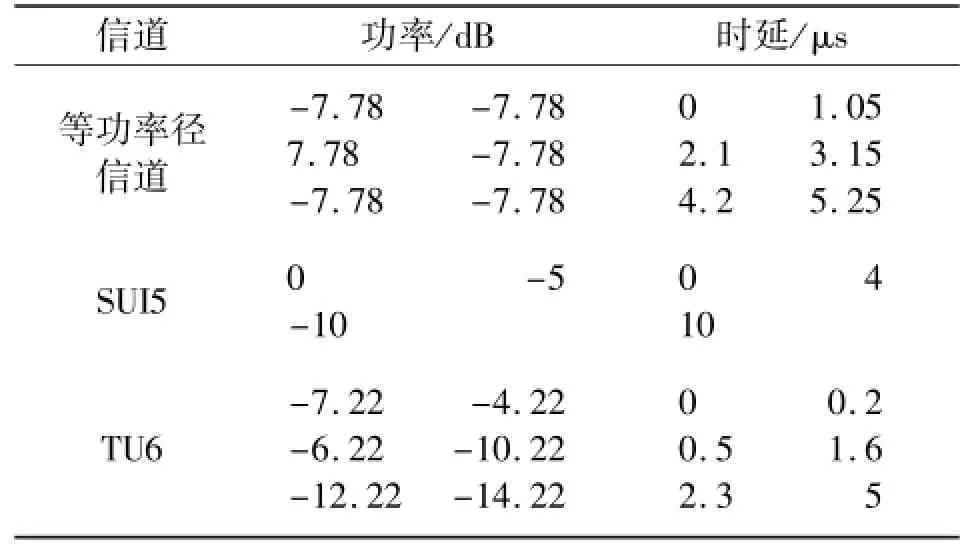
表2 信道模型参数设置Table 2 Channel model parameter settings

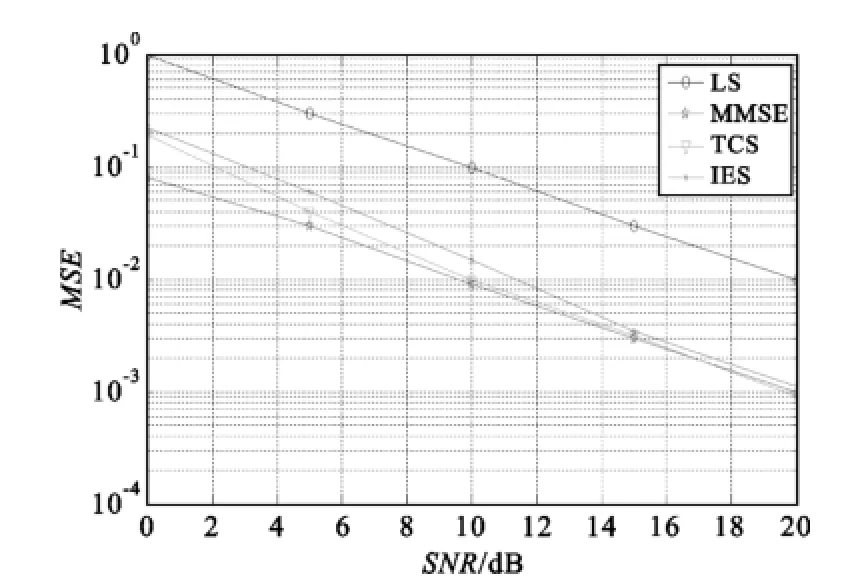
图2 等功率径下算法MSE信性对比Fig.2 Algorithm MSE performance comparison chart under equal power multi-path

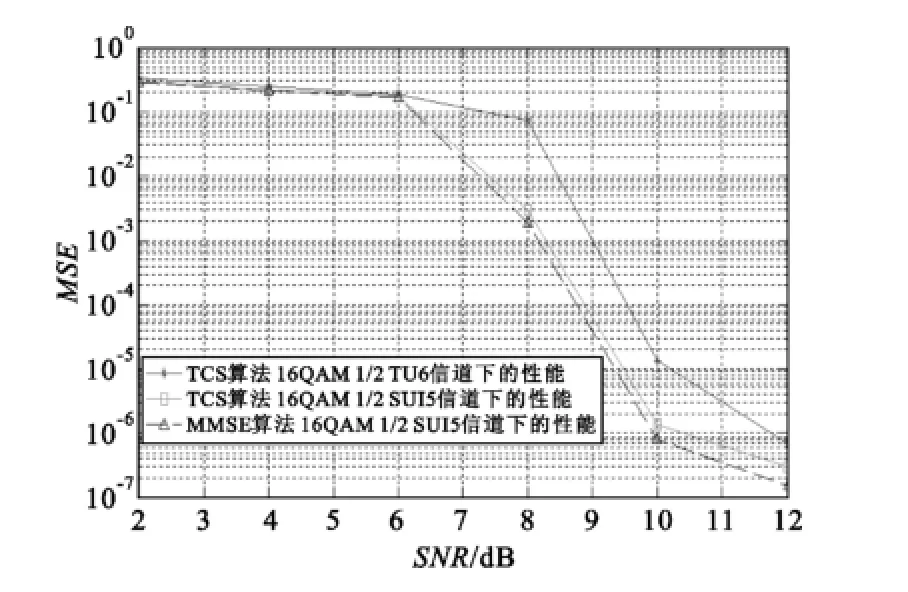
图3 10 M带宽波形在静止信道模型下的性能(TCS)Fig.3 Performance of 10 MHz bandwidth waveform under the channel model(static)

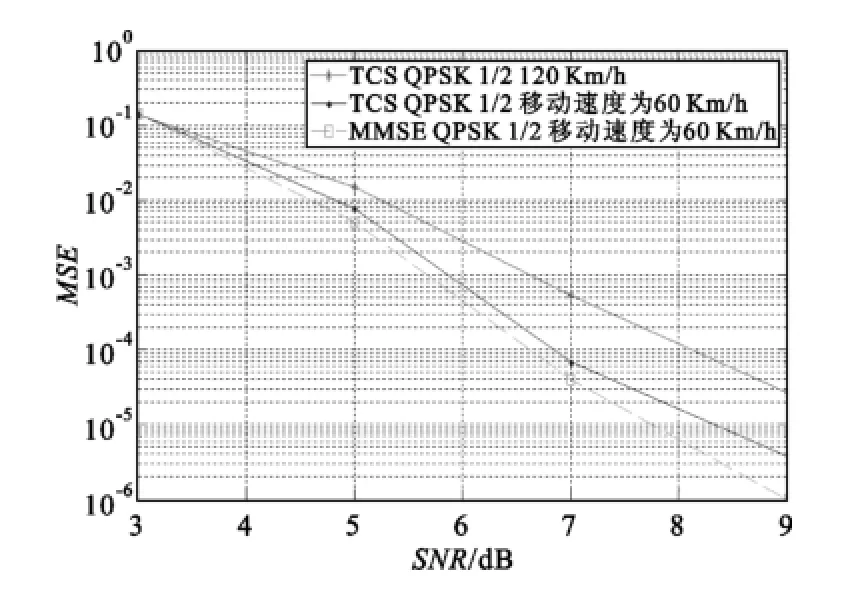
图4 10 M带宽波形在移动信道模型下的性能(TCS)Fig.4 Performance of 10 MHz bandwidth waveform under mobile channel model

由图2可以看出,门限选择算法(TCS)和能量即时算法算法(IES)与LS算法比较都有比较大的提升,以误差5e-2为例,门限选择算法TCS相比LS算法的MSE(均方误差)提升8 dB左右,能量立即算法比LS算法MSE(均方误差)提升约7 dB左右,可见TCS(门限选择)算法法更接近于MMSE算法的性能。同时图3和图4分别给出采用TCS(门限选择算法)的波形在静止信道模型及移动信道模型下的性能。在图3中,在相同的信道条件下(SUI5信道下),TCS算法的性能基本与MMSE算法性能接近,性能比MMSE算法性能差约0.3～0.5 dB左右。如图4所示,TCS算法在移动信道下的性能与MMSE算法的性能也比较接近。但是运算量却大大减少,便于工程实现。

4 结 语

文中提出了OFDM基于导频辅助信息的信道估计方法存在的问题,在工程应用中信道的统计信息在接收端很难得到。我们的目标就是通过选择最优的信道冲激响应集来获得比较好的MSE性能,而且不需要信道自相关阵等复杂的先验信道统计信息。基于此,我们提出了门限选择算法和即时能量选择算法等两种方法,通过仿真验证,两种方法信道估计MSE(均方误差)的性能已接近MMSE算法性能,但算法的运算量大大减少,具备工程可实现性及工程实用价值。同时,我们给出了该算法在静止及低速移动信道模型下的性能。在高速移动信道下的可工程实现的处理方法仍需进一步研究。

[1] 丛键,张玉哲,张海燕.战术电台组网波形中的多址技术研究[J].通信技术,2013,46(08):81-84.

CONG Jian,ZHANG Yu-zhe,ZHANG Hai-yan.Multi-Access Technology of Networking Waveform in Tactical Radio[J].Communications Technology,2013,46(08): 81-84.

[2] HOEHER P.,KAISER S.,and ROBERTSON P..Twodimensional Pilot Symbol Aided Channel Estimation by Wiener Filtering[C]//1997 IEEE International Conf. AtlanticCity NJ:IEEE,1997.:1845-1848.

[3] HOEHER P.,KAISER S.,and ROBERTSON P.Pilotsymbol-aided Channel Estimation in Time and Frequency [C]//Theory Mini-Conf.within IEEE Global Telecommun.Conf.AtlanticCity NJ:IEEE,1997:90-96.

[4] 吕良,郭宝龙,石磊.LTE下行信道估计方法的优化[J].计算机工程与应用.2011,47(26):58-60.

LV liang,GUO Bao-long,SHI Lei.Optimization of LTE Downlink Channel Estimation Method[J].Computer Engineering and Applications.2011.47(26):58-60.

[5] EDFORS O.,SANDELL M.,VAN DE BEEK J.J., etc.OFDM Channel Estimation by Singular Value Decomposition[J].IEEE Trans.Commun.1998,46(07): 931-939.

[6] EDFORS O.,SANDELL M.,VAN DE BEEK J.J., etc.Analysis of DFT-based Channel Estimators for OFDM[J].Wireless Personal Commun.2000,12(01): 55-70.

[7] 巴特尔,江彬,范晓俊等.基于对称扩展DFT变换的OFDM系统信道估计方法[J].东南大学学报.2012,42 (01):1-6.

BA te-er,JIANG Bin,FAN Xiao-jun.Chanel Estimation Method based on Symmetric Extended DFT Transform in OFDM System[J].Journal of Southeast University. 2012,42(01):1-6.

[8] MINN H.and BHARGAVA V.K..an Investigation into Time-Domain Approach for OFDM Channel Estimation [J].IEEE Trans.Broadcast.2006,46(04):240-248.

[9] 周冰,刘强.OFDM系统中基于导频信道估计方法的研究[J].中国电子科学研究院学报.2011,6(04): 396-400.

ZHOU Bing,LIU Qiang.Investigation of Pilot Symbol Aided Channel Estimation Methods for Wireless OFDM Systems[J].Journal of CAEIT,2011.6(4):396-400.

ZHOU Bing(1977-),female,M.Sci.,engineer majoring in broadband waveform physical layer design and communication signal processing.

杨建平(1985—),男,硕士,工程师,主要研究方向为无线传输技术及FPGA算法设计。

YANG Jian-ping(1985-),male,M.Sci.,engineer,majoring in wireless transmission technology and design of FPGA engineering algorithm.

Channel Estimation Optimization based on None-Knowledge of Channel Statistics in OFDM

ZHOU Bing,YANG Jian-ping
(No.30 Institute of CETC,Chengdu Sichuan 610041,China)

MMSE and its variant——LMMSE are usually used in the optimization of traditional channel estimation algorithm,and however,this kind of algorithm,due to its requirement for much knowledge of channel statistics(KCS),is very complex and difficult in implementation.In this paper,OFDM data-aided channel estimation based on the decimation of channel impulse response(CIR)is proposed,which selects the most significiant samples(MSS)and gets rid of the noise jamming,so as to make the performance reach the MMSE channel estimation performance,while avoiding the requirement for a-prior knowledge of channel statistics (KCS).The novel TCS(Threshold Crossing Selection)and IES(Instaneous Energy Selection)are also proposed in this paper.Simulation shows that the both agorithms are close to MMSE algorithm in performance, while have a sharp decrease in operand,and thus of great value in engineering implementation.

OFDM;channel estimation;MMSE;none knowledge of channel statistics

TN924+.3

A

1002-0802(2014)10-1130-05

10.3969/j.issn.1002-0802.2014.10.005

周 冰(1977—),女,硕士,工程师,主要研究方向为宽带波形物理层设计及通信信号处理;

2014-07-02;

2014-08-14 Received date：2014-07-02;Revised date：2014-08-14