星地一体化导航系统星间链路仿真及分析*

侯 颖,米志超,于卫波,牛大伟

(解放军理工大学通信工程学院,江苏南京210007)

星地一体化导航系统星间链路仿真及分析*

侯 颖,米志超,于卫波,牛大伟

(解放军理工大学通信工程学院,江苏南京210007)

在导航卫星系统中,为了解决星间链路拓扑规划不合理而导致的星地信息传输时延大的问题,提出了一种新的星间链路规划方法。该方法优先考虑星地间的可视覆盖关系,保证卫星与地面站之间实时的信息传输。利用STK仿真软件构建了卫星网络拓扑,进而利用OPNET仿真软件完成了性能仿真验证。仿真结果表明,新的拓扑减小了星地数据传输的跳数和端到端时延,符合星地一体化的需求。

卫星导航系统 星地一体化 星间链路 仿真

0 引 言

随着卫星应用需求的日益发展,卫星导航系统已经成为国家的一项重要的战略性基础资源[1]。建立星间链路可以提高导航系统的抗毁能力和自主运行能力,增强卫星网络的灵活性和稳定性。在导航卫星星座内建立星间链路,组建卫星网络(Satellite Networks)[2],已经成为导航卫星系统发展的必然趋势[3]。由于卫星上可搭载的天线数量通常少于可建立星间链路的卫星数量,因此卫星运行时要在其可视卫星中进行有选择的建链。

国外对于卫星星间链路的研究工作开展地比较早,现在已经在国际上得到了较为广泛的应用和推广,美国的GPS BLOCK IIR[4]导航卫星系统是目前在轨导航星座中唯一实现星间链路的系统,通过星间链路测距和通信,可以在没有地面站支持的条件下维持180天的自主导航。

国内部分学者也从理论上对星间链路进行了初步的研究和分析,文献[5]对卫星通信系统的星间链路参数进行了分析;文献[6]提出了星座星间链路的构建准则及优化设计;文献[7]针对卫星点波束覆盖的问题提出了卫星点波束中心选取算法,;文献[8]提出了一种兼顾导航卫星系统进行星间测距和数据通信的星间链路分配算法。

但现有的大部分星间链路的研究都是在通信卫星系统的基础上展开,侧重于卫星星座的全连通性和通信性能优化。导航卫星系统与通信卫星系统在需求与用途方面都有较大区别,其大部分功率用于播发导航信号,针对通信卫星系统的研究成果不能直接应用到导航卫星系统[9]。而针对导航卫星的研究又大多侧重于星间数据通信性能优化,忽略了卫星与地面站的数据传输性能,即导航系统的星地一体化特性。

导航卫星系统中的信息传输主要包括三方面:卫星与地面站之间的信息传输,卫星与卫星之间的信息传输,以及地面站与用户目标之间的应用数据传输。对导航卫星系统而言,卫星间本身信息交互的需求并不强烈,最主要的信息传输是地面站与卫星间的业务信息、链路管理信息等的上注与下传。星间链路的设计必须要关注卫星与地面站之间的信息传递和信息中继问题,这也是文中的研究重点。

另一方面,针对导航卫星系统的星间链路研究多将研究重点集中在层间星间链路和异轨星间链路方面,对于同轨星间链路往往做一个简单的设定。事实上,同轨卫星虽然几何关系相对固定,但是不同的同轨星间链路拓扑也会对导航卫星系统的星地一体化特性产生较大影响,有必要对此进行分析研究。

综上所述,文中以一种典型的Walker型导航星座系统为研究基础,着重考虑卫星与地面站的数据传输性能,仿真分析了同轨星间链路拓扑对系统星地一体化性能的影响,研究结果对于导航星座系统的同轨星间链路的建立具备参考意义。

1 星间链路规划原理描述

1.1 可见关系要求

为保证系统正常运行,导航卫星星座应满足一定的可见性要求,主要包括导航系统与地面站的可见性和卫星与卫星之间的可见性两方面。

地面站与导航卫星系统的可见取决于卫星对地球表面的覆盖特性,当卫星与地面站可见时,卫星可以直接与地面站通过星地链路建立通信传输渠道,否则就需要通过星间链路中继进行信息传输。

卫星与卫星之间的可见关系有三种可能,始终可见、间歇可见和始终不可见,卫星之间可建立星间链路的前提条件是两卫星可见。同一轨道平面内各卫星的相对位置关系固定,不存在距离和角度的变化,可见的同轨卫星间可以建立稳定的永久星间链路。不同轨道平面的两颗卫星能否建立星间链路则与卫星相对位置的变化密切相关,始终可见的卫星可以建立固定的链路拓扑规划,间歇可见的卫星只能采用动态的拓扑规划。

1.2 数学描述

星间链路设计算法的输入是根据导航系统运行规律而得出的一系列固定的可见关系,包括卫星与地面站和卫星与卫星之间的可见关系,可以由STK卫星仿真软件产生。算法的输出是一个计算周期内导航系统的链路分配方案。

可见关系通过两个0-1矩阵V1和V2来描述。V1=[Vai]用来描述卫星与地面站之间的可见关系, a为系统中的地面站节点,i为系统中的卫星节点。V2=[Vij]用来描述卫星之间的可见关系,i与j均为系统中的卫星节点。矩阵中的元素v=1表示两节点可见,v=0则表示两节点不可见。导航系统星间链路分配方案通过0-1矩阵L=[lij]来描述。i与j均为系统中的卫星节点,元素lij=1表示在卫星i与卫星j之间建立星间链路,lij=0表示在卫星i与卫星j之间不建立星间链路。

因此,星间链路的规划问题可以描述为:给定两个可视矩阵V1和V2,获取链路分配矩阵L,且对于任意的lij=1,在V2中相应的vij=1,即卫星之间可见是建立星间链路的前提。

2 星间链路规划过程

文中提出的星间链路规划,优先保证卫星到地面站数据传输的跳数最小化,核心思想是:当卫星可以见到地面站时,卫星直接与地面站通信;当卫星不可以见到地面站时,在其可见卫星中选择可以与地面站直接通信的卫星进行中继,且优先考虑星间链路状态稳定的同轨卫星;当卫星及其可见卫星均与地面站不可见,则按照最短路径算法选取合适路径。具体步骤如下所示:

Step1:初始化,输入星地可见关系矩阵V1和卫星之间可见关系矩阵V2;

Step2:星地可见关系筛选,在矩阵V1中选取所有当vai=0时vaj=1的节点,即当卫星与地面站不可见时,可以与地面站直接通信的卫星节点;

Step3:星间可见关系筛选,在矩阵V2中选取Vij=1的节点对,即筛选出相互可见、可以建立星间链路的卫星;

Step4:将step2、step3的筛选结果取交集,在矩阵L中置lij=1,作为建链的备选集合,并在每次选择中优先选择对地可见概率大的节点建链。

3 场景建模与性能仿真分析

3.1 仿真环境描述

文中采用卫星仿真工具包STK搭建卫星网络仿真环境,完成场景建模。从上个世纪60年代起,人们先后提出了很多星座设计方法[10]。实践证明,三轨道面星座是下一代卫星导航系统星座设计的趋势。文中的导航星座采用文献[11]中提出的典型导航星座模型,24颗中轨道(MEO)卫星均匀分布在3个轨道面上,构成标准的Walker24/3/2星座[12]。轨道高度为21 500 km,轨道倾角55°,星上天线波束数量为4,星座运行周期约12h50m。对第x轨道面(x=1、2、3)的8颗卫星顺时针标记为Mx1、Mx2、……、Mx2。n个地面站构成集合E={地面站1,地面站2,……,地面站n}。

为了更直观的分析星地数据传输性能,文中在OPNET[13]中进行了相关参数的仿真测试。为便于分析,在网络仿真中仅建立包含第一轨道面的8颗卫星和地面站集合的网络拓扑结构,路由算法采用Dijkstra算法。仿真中,数据由卫星节点发送给地面站,仿真时间为24h,参数指标为卫星到地面站数据传输的跳数和端到端时延。

根据Walker星座的空间对称性可知,轨道面中任一卫星的几何特性都可以代表该星座中所有星的几何特性,因此文中只需讨论析第一颗卫星M11的各项参数,就可以推导出其他卫星的相关参数。

3.2 可见关系分析

任意两颗卫星可以构建星间链路,以及卫星可以与地面站直接通信的首要条件,均为两节点处于相互可见状态。在分析星间链路之前,首先要对卫星与地面站之间的可见概率进行分析。

在STK仿真软件中生成一个系统运行周期内卫星与地面站的可见性分析报告,当M11对地面站不可见时,其它各卫星对地面站的可见概率如表1所示,依次为M15,M14,M16,M13,M17,M12,M18。

表1 对地面站的可见概率Table 1 Probability to be visible for the earth

分析M11与同轨道面内的各颗卫星的可见关系可知,卫星M11与卫星M15相位差为180°,由于地球的阻挡效应,两颗卫星始终处于不可见状态, M15虽然对地面站可见概率最大,但并不能与M11建立星间链路。而M11与同轨道其他的6颗卫星则始终处于可见状态。在同一轨道平面内卫星间几何关系相对固定,不存在距离和角度的变化,因此M11可以与M12、M1、M14、M16、M17、M18建立永久星间链路。

在文中的导航星座中,以每颗MEO卫星可建立两条同轨星间链路为例,通常情况下,Walker星座中的层内星间链路拓扑为四链路模式,每颗卫星分别与同轨道平面内的两颗卫星,相邻轨道平面的两颗卫星建立星间链路[14]。在同轨星间链路的建立上,现有研究往往出于简单考虑,选择每颗卫星前后相邻两颗卫星,即距离最近的两颗卫星。但事实上,考虑到卫星与地面站的可视覆盖关系,相邻卫星的空间几何特性并不一定是最好的,M11前后相邻的两颗卫星M12和M18,对地面站的可见概率恰好是最小的。按照文中的规划方法,则选取的是对地面站可见概率最大的两颗卫星,M14和M16。

根据星座对称性,两种方法形成的同轨星间链路拓扑模式如图1所示。

图1 同轨星间链路拓扑Fig.1 Topologies of intra-orbit ISLs

为表述方便,文中将两种拓扑分别命名为环形拓扑和八角星拓扑。当卫星本身无法和地面站直接通信,必须借助其他卫星进行数据转发时,环形拓扑中,与源节点卫星建立链路的两颗卫星有大于80%的概率同样无法与地面站直接通信,还需要继续进行数据转发,直到数据到达可与地面站直接通信的卫星;而八角星拓扑中,与源节点卫星建立链路的两颗卫星可以与地面站直接通信的概率超过了50%,有很大的概率可以在较小的跳数内完成数据对地面站的传输。

3.3 跳数分析

跳数是指分组从源节点产生经转发投递到目的节点的过程中经过的中继节点的个数。图2和图3分别给出了在一个仿真周期内,数据从卫星发送到地面站传输的实时跳数和平均跳数的比较。

图2 跳数比较Fig.2 Hops of two topologies

图3 平均跳数比较Fig.3 Average hops of two topologies

由图2和图3可以看出,在大多数时间内八角星拓扑的数据传输的跳数要小于环形拓扑,并且在一个仿真周期内,环形拓扑的平均跳数约为2.4,八角星拓扑的平均跳数约为1.9,八角星拓扑的数据传输平均跳数也小于环形拓扑,与上文的分析结果一致。

3.4 分组端到端时延分析

分组端到端时延是指分组成功投递到目的节点的时刻与源节点产生该分组时刻的差值,是QoS (Quality of Service)最重要的参数之一。当不考虑排队和处理时延的情况下,图4给出了在一个仿真周期内,数据从卫星发送到地面站端到端时延对比情况(左为环形拓扑,右为八角星拓扑)。

图4 分组端到端时延比较Fig.4 End-to-End delay of two topologies

从图4可以看出,在大部分时间里,环形拓扑的端到端传输时延值要大于八角星拓扑。同时也看到,八角星拓扑存在几个高峰,下面分析这几个高时延时段出现的原因。几个时延高峰出现的时间段分别为115～129 min,180～243 min,268～309 min,以M11卫星到地面站的数据传输过程为例,表2展示了这些时间段内地面站的可见卫星以及两种拓扑的卫星到地面站数据传输路径。

表2 可见卫星和数据传播路径Table 2 Visibility relationship and data path

在这几个高时延段,地面站可以看到的卫星多为M11卫星的相邻卫星(M12、M13)或相对卫星(M15),由于环形拓扑选择建链的卫星为相邻卫星,这种情况下环形拓扑的星地数据传输跳数要等于或小于八角星拓扑。又因为八角星拓扑星间一跳距离约是环形拓扑的2.4倍,因此这几个时间段间内八角星拓扑的星地间数据传输距离要高于环形拓扑,产生了较大的端到端时延。

上述分析中的端到端时延仅考虑了传播时延,时延大小只与数据的传输距离有关。然而事实上,分组端到端时延还包括数据的排队和处理时延,即数据每经过一跳在中转节点上耗费的时间。下面将排队和处理时延加入考虑范围。在一个仿真周期时间内,当排队和处理时延值为0 s、0.05 s、0.10 s、0.15 s、0.20 s时,同轨星间链路为环形拓扑和八角形拓扑的情况下,数据从卫星发送到地面站平均时延变化,如图5所示。图5中横坐标为排队和处理时延取值。

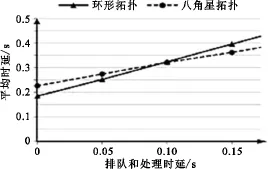
图5 平均分组端到端时延比较Fig.5 Average end-to-end delay of two topologies

由图5可以看出,当不考虑排队和处理时延或排队和处理时延值较小时,八角星拓扑相比环形拓扑虽然具有更优的路径跳数,但因为几个高时延区的存在,八角形拓扑星地数据传输的平均分组端到端时延较大。但当排队和处理增大至0.1s时,两种拓扑的平均分组端到端时延基本相同。当排队和处理时延值继续增加时,八角星拓扑的跳数优势得以显现,与环形拓扑相比具有更优的分组平均端到端时延。所以为了使导航系统具有更优的星地一体化性能,同轨星间链路拓扑的选择最好立足于系统的实际情况,而不能只是简单的选择相邻卫星构建星间链路。

4 结 语

现有的星间链路研究往往以卫星之间通信性能的优化为目标,以异轨星间链路和层间星间链路为重点,对同轨星间链路只做简单的设定,很少考虑导航星座系统的星地一体化性能的要求和同轨星间链路拓扑的选择。文中立足于一种典型的导航星座系统,提出了一种星间链路拓扑规划方法,并着重研究了同轨星间链路拓扑模型对于卫星和地面站之间数据传输性能的影响。

仿真结果表明,在一个仿真周期的大部分时间内,相比于传统的环形拓扑,文中提出的八角星拓扑具有更优的跳数指标。在排队和处理时延较小时,环形拓扑具有更优的分组端到端时延,但随着排队和处理时延的增大,八角星拓扑的端到端时延优势将越来越大,因此同轨星间链路拓扑的选择与系统中节点对数据的排队和处理性能有关。当数据在节点的排队和处理时延较大时,应优先选择八角星拓扑,反之则可选择环形拓扑。文中的结论为导航卫星系统同轨星间链路拓扑的选择提供了一定的参考。

文中只是一个初步简单的探索,在接下来的工作中,将对星地数据传输性能的优化做进一步的研究,考虑消除八角形拓扑模型下的星地数据传输的高时延期,通过在相应时间段内接入异轨卫星或异层卫星来减少星地间数据传输的跳数和端到端时延,探讨异轨星间链路和层间星间链路对导航星座星地一体化性能的影响。

[1] 刘会杰,张乃通.全球导航卫星系统的星座可见性研究[J].系统工程与电子技术,2000,22(05):23-25.

LIU Hui-jie,ZHANG Nai-tong.Research on Constellation Visibility for Global Navigation Satellite System[J].Systems Engineering and Electronics,2000,22(05):23-25.

[2] LUDERS R D.Satellite Networks for Continuous zonal Coverage[J].Journal of the American Rocket Society. 1961(31):179-184.

[3] CHACOSA P.Autonomous Navigation and Crosslink Communication Systems for SpaceApplications[J]. Johns Hopkins APL Technical Digest,2001,22(02): 135-141.

[4] MONTENBRUCK O,HUGENTOBLER U,DACH R.Apparent Clock Variations of the Block IIF-1(SVN62)GPS Satellite[J].GPS Solutions,2012,16(03):303-313.

[5] 李赞,张乃通.卫星移动通信系统星间链路参数分析[J].通信学报,2000,21(06):92-96.

LI Zan,ZHANG Nai-tong.ISL Spacial Paremeters'A-nalysis of Mobile Satellite Communication System[J]. Journal on Communications,2000,21(06):92-96.

[6] 范丽,张育林.区域覆盖混合星座设计[J].航天控制, 2007,25(06):52-55.

FAN Li,ZHANG Yu-lin.Regional Coverage Hybrid Constellation Design[J].Aerospace Control,2007,25 (06):52-55.

[7] 鲍凯,徐慨,项顺祥,等.基于STK的点波束覆盖分析与仿真[J].通信技术,2013,46(01):17-19.

BAO Kai,XU Kai,XIANG Shun-xiang,et al.Analysis and Simulation of Spot Beam Coverage based on STK [J].Communications Technology,2013,46(01):17-19.

[8] 石磊玉,向为,唐小妹,等.一种兼顾卫星导航系统星间观测及通信的链路分配算法[J].宇航学报,2011, 32(09):1971-1977.

SHI Lei-yu,XIANG Wei,TANG Xiao-mei,et al.A Link Assignment Algorithm Applicable to Crosslink Ranging and Data Exchange for Satellite Navigation System[J].Journal of Astronautics,2011,32(09):1971-1977.

[9] WANG Jing,XU Zhen,LIU Feng.Modeling and Simulation of Satellite-earth Integrated Routing Planning[J]. Computer Simulation,2011,28(07):142-145,176.

[10] LO M W.Satellite Constellation Design[J].IEEE Computing in Science and Engineering,1999,21 (01):58-67.

[11] 谭述森.北斗卫星导航系统的发展与思考[J].宇航学报,2008,29(02):391-396.

TAN Shu-sen.Development and Thought of Compass Navigation Satellite System[J].Journal of Astronautics,2008,29(02):391-396.

[12] WALKER J G.Satellite Constellations[J].Journal of the British Interplanetary Society,1984(38):559-571.

[13] HNATYSHIN Y V,LOBO F A.Undergraduate Data Communications and Networking Projects Using OPNET and Wireshark Software[J].SigcseBulletin,2008, 40(01):241-245.

[14] 佘春东,王俊峰,刘立祥,等.Walker星座卫星网络拓扑结构动态性分析[J].通信学报,2006,27(08): 45-51.

SHE Chun-dong,WANG Jun-feng,LIU Li-xiang,et al.Topological Dynamics Analysis of Walker-constellation Satellite Networks[J].Journal on Communications,2006,27(08):45-51.

HOU Ying(1989-),female,graduate student,mainly engaged in the research of satellite navigation system.

米志超(1974—),男,博士,副教授,主要研究方向为卫星组网技术;

MI Zhi-chao(1974-),male,Ph.D.,associate professor, mainly engaged in the research of satellite network technology.

于卫波(1975—),男,博士,讲师,主要研究方向为无线分组网络;

YU Wei-bo(1975-),male,Ph.D.,lecturer,mainly engaged in the research of wireless packet network.

牛大伟(1979—),男,博士,讲师,主要研究方向为无线自组网协议。

NIU Da-wei(1979-),male,Ph.D.,lecturer,mainly engaged in the research of wireless ad hoc network protocol.

Simulation and Analysis on Inter-Satellite Links of Satellite-Earth Integrated Navigation System

HOU Ying,MI Zhi-chao,YU Wei-bo,NIU Da-wei
(College of Communication Engineering,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

A novel inter-satellite links(ISLs)algorithm is proposed to solve the increase problem of satellite -to-earth transferring delay caused by unreasonable ISLs topology planning in the navigation satellite system.The algorithm pays the utmost attention to the satellite-earth visual coverage,and ensures the realtime information transmission between the satellites and the ground stations.The satellite network topology is constructed with STK simulation software,and the performance simulation completed with OPNET simulation software.The simulation result indicates that the new topology could reduce the satellite-to-earth transferring hops and end-to-end delay,and thus meet the demand of satellite-earth integrated system.

satellite navigation system;satellite-earth integration;ISLs;simulation

TP391.9

A

1002-0802(2014)02-0145-05

10.3969/j.issn.1002-0802.2014.02.005

侯 颖(1989—),女,硕士研究生,主要研究方向为导航卫星系统;

国家自然科学基金(No.61103224);江苏省自然科学基金(No.BK2011118)

Foundation Item:National Natural Science Foundation(No.61103224);Jiangsu Province Natural Science Foundation(No.BK2011118)