蚁群算法中基于分布估计的量子信息素控制研究

翟亚红，徐龙艳

（湖北汽车工业学院电气与信息工程学院，湖北十堰442002）

0 引 言

蚁群算法已发展成为求解复杂优化问题的有效工具，但由于其信息素控制方法主要是面向离散问题设计的，故难以对连续优化问题进行高效求解。因此，研究人员提出了一些新的信息素表示方法，其中基于可行解的信息素表示是常见的一种方法［1］。该方法特点是结构及控制过程相对简单，曾作为蚁群算法求解连续优化问题的主要解决方案。但这种依靠若干个可行解的信息素驻留方式，限制了蚂蚁搜索的视野，容易使蚁群算法陷入局部最优解。Krzysztof Socha与Dorigo共同提出了一种面向连续问题的基于分布估计的信息素模型［2］，是对连续问题求解比较流行的另一种方法，它所采用的分布估计方法能够从宏观角度把握进化方向，有助于提高对蚂蚁搜索的全局搜索能力。然而，由于其概率模型比较单一，缺乏对蚂蚁搜索的多样性指导，亦容易使蚁群算法陷入局部最优解。

在蚁群算法中，信息素是实现群集智能的关键，是人工蚂蚁实现间接通信、完成群体协作的重要媒介。已有的研究表明，信息素的留存、初始化、播撒及挥发等控制策略，在很大程度上影响着蚁群算法的优化性能。因此，进一步优化信息素控制策略，对于改善蚁群算法的优化性能、扩展其应用领域，具有重要的研究价值和现实意义。基于课题组的前期工作，本文以信息素控制策略为研究重点，通过引入分布估计方法以及量子态叠加机制等，对蚁群算法在连续问题求解中的信息素控制方法进行新的探索。

1 量子态叠加原理与分布估计算法

1.1 量子态叠加原理

微观粒子所处的状态即量子态具有叠加特性，一个量子态可以由态空间中的多个基态线性叠加而成。量子态叠加示意图如图1所示。

Kuk－Hyun Han等人提出的量子进化算法是目前为止求解组合优化问题中最有效的量子进化算法之一。与普通的进化算法相比，该算法可以在提高搜索多样性的同时降低群体规模，避免了算法陷入局部最优解。

文献［3，4］通过引入量子比特、量子旋转门及量子非门等技术，提出了一种用于求解连续优化问题的连续量子蚁群算法（continuous quantum ant colony algorithm，CQACA）。该算法使用一组量子比特的概率幅表示蚂蚁当前位置，蚂蚁采用量子旋转门、非门等方法对量子比特进行操作，实现位置移动。实验显示该算法体现了量子计算的高效性，但限制了蚂蚁的全局寻优能力，导致该算法的求解精度较差。量子比特示意图如图2所示。

图2 量子比特

1.2 分布估计算法

近年来新兴起了一种随机优化算法即分布估计算法（estimation of distribution algorithm，EDA）［5］，它将统计学与传统的遗传算法相结合，成为当前计算领域的研究热点。分布估计算法与传统的遗传算法的基本流程如图3所示。

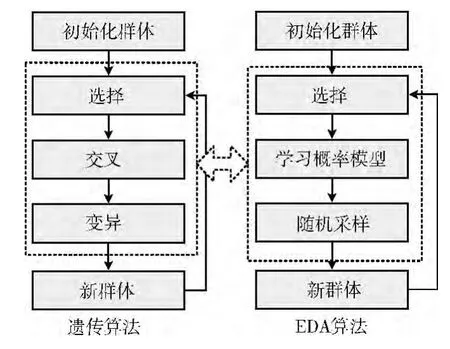
图3 分布估计算法与遗传算法的基本流程

分布估计算法能够从宏观角度把握进化的趋势，因此能够在求解连续优化问题时很好的从全局角度搜索最优路径。受其启发，Socha和Dorigo合作提出了一种基于分布估计的信息素模型［2］，使用描述最优解在空间分布的概率估计模型表示信息素，以改善蚁群算法在求解连续优化问题时信息素表示能力的不足。通过人工蚂蚁对信息素进行随机采样创建可行解，并以所创建解的信息作为依据更新信息素。经过实验证明，这种基于分布估计的信息素模型，在很大程度上能够改善蚂蚁在连续空间上的全局搜索能力，能够有效提高蚁群算法在求解连续问题时的整体优化性能。不过，该模型还存在着一些不足，主要表现在信息素更新过程中的大量排序工作耗费了较大的计算代价，并且表示信息素的概率模型较单一而限制了蚂蚁搜索的多样性等方面。

2 分布估计的量子信息素模型及其蚁群算法

本文将分布估计算法和量子态叠加机制思想相结合，设计了一种面向连续优化问题的基于分布估计的量子信息素模型（quantum pheromone and its control strategy based on estimation of distribution，QPED）及其蚁群算法。

2.1 分布估计的量子信息素模型基本框架

基于分布估计的量子信息素模型的基本框架如图4所示。其中，量子信息素Ψ被看作一个量子态叠加，由k个量子基态Ψi（i＝1，2，…，k）按照量子态叠加原理线性叠加而成。

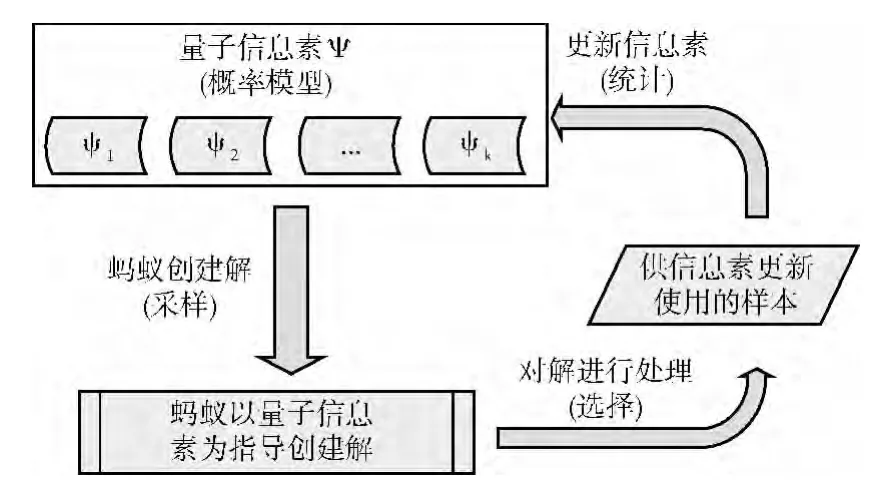
图4 基于分布估计的量子信息素模型

每个量子基态Ψi采用简单的正态分布表示，ci为Ψi的叠加系数，分别是其期望值和方差，表示基态Ψi第j维的正态分布。

每个量子基态Ψi由一个描述最优解在空间中分布的概率模型表示，如下所示

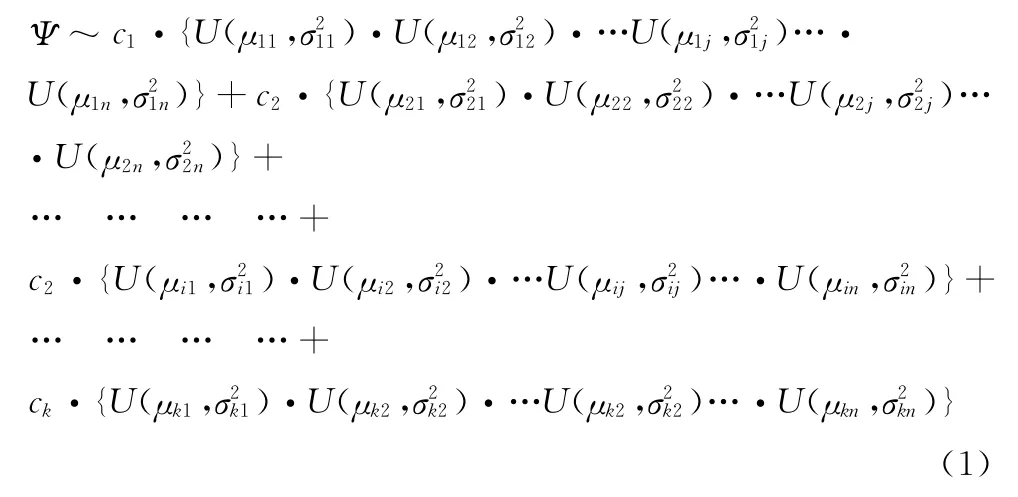
2.2 量子信息素的数据结构

量子信息素的数据结构采用数组表示，如图5所示。采用一个大小为k×（n＋1）的数组（k为量子信息素的基态个数，n为解空间维数），存储量子信息素Ψ的主要信息。其中，第i行用来表示基态Ψi的有关信息，包括其叠加系数ci，各维的分布期望值μij。

量子信息素中各正态分布的方差取值十分重要，如果取值过大，则蚂蚁搜索范围过与广泛，缺乏针对性，便会降低蚁群算法的收敛速度；反之，如果取值过小，则蚂蚁搜索范围会过窄，容易使算法陷入局部最优状态。基于以上考虑，引入了一种自适应方差计算方法，如下所示

为了提高蚂蚁之间通信的时效性，增强群体的协作能力，采用了在线计算的原则进行方差值计算，即只有在蚂蚁创建解的过程中需要用到某正态分布时，才对其进行方差计算。

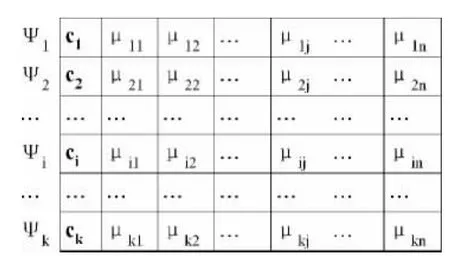
图5 量子信息素模型的数据结构

2.3 分布估计的量子蚁群算法

基于量子信息素模型和分布估计算法，提出了一种基于分布估计的量子蚁群算法（quantum－inspired ant colony optimization for continuous domain，QACOC），QACOC算法包括蚂蚁创建解和信息素更新两个方面，其算法流程描述如下:

根据各基态的叠加系数从量子信息素中选取一个量子基态Ψi；

根据基态和所计算的方差序列，随机采L个样本；

从L个样本中选取最优的一个作为该只蚂蚁创建的解Xant保留；｝

2.3.1 蚂蚁创建解

蚂蚁根据各量子基态叠加系数ci从量子信息素Ψ中选取一个量子基态Ψi作为采样对象，计算该基态的各维分布的方差。然后，对该基态各维上的正态分布进行随机采样，计算出问题的可行解。在采样过程中，个别采样值可能会超出定义域范围，使其计算得到的解成为非可行解。为避免此种情况发生，保证蚂蚁在每次采样后都能获得可行解，算法中对超越定义域范围的采样值采用反弹法［6－8］进行处理，保证采样值不超出定义域范围。反弹法算法描述如下:

2.3.2 信息素更新

量子信息素的更新操作主要包括期望值和叠加系数更新两个方面。首先，蚂蚁将自己创建的可行解Xant与采样对象基态Ψi的期望值序列Ui＝（μi1，…，μin）进行对比，如果F（Xant）优于F（Ui），则另Ui＝Xant，否则，不做任何操作。其次，为了避免蚂蚁过度集中地选择某一基态，在蚂蚁完成更新期望值序列后，根据ci＝ci×ρ（ρ为叠加系数的更新参数，0≤ρ≤1），更新其采样对象Ψi的叠加系数。另外在每次迭代开始时可将基态的叠加系数都设为1.0，从而增强信息素对蚂蚁搜索的多样性和全局性。

3 仿真结果及实验分析

本文从收敛性能和求解精度两个方面对QACOC和ACOR［2］算法进行了实验分析，算法性能测试采用3种常用的连续函数实现［9，10］。表1给出了3种函数的表达式及其定义域。

表1 评价函数

3.1 收敛性能分析

QACOC和ACOR算法在f1，、f2和f3这3个评价函数上的收敛趋势如图6所示。其中，纵坐标表示函数值，横坐标表示函数对比次数，即在算法运行中对解的目标函数值进行对比的次数。采样这项指标，可以避免因实验人员的主观因素（如编程习惯等）对算法评价时造成客观性的影响。

图6中的曲线，表示了QACOC和ACOR两种算法随函数对比次数增加的收敛趋势。其中，由“◆”标记的深色曲线是QACOC算法的收敛曲线走势；由“■”标记的浅色曲线是ACOR算法的收敛曲线走势。显而易见，在3个函数实例上，QACOC算法的收敛速度均明显优于ACOR算法。例如，在f1函数上，QACOC算法获得小于0.1的解需要160次函数对比，而ACOR算法需要340次；在f2上，QACOC算法只耗费240次函数对比就能得到小于0.1的解，ACOR算法需要740次；同样，在f3上，QACOC算法只需要120次函数对比就能得到小于0.05的解，而ACOR算法需要280次。

实验结果表明，QACOC算法的收敛速度明显优于ACOR算法。其原因是QACOC算法量子信息素在更新过程中不需要排序，节省了大量的排序时间，而ACOR算法将大量时间花费在了信息素更新的排序上，降低了算法的执行效率。

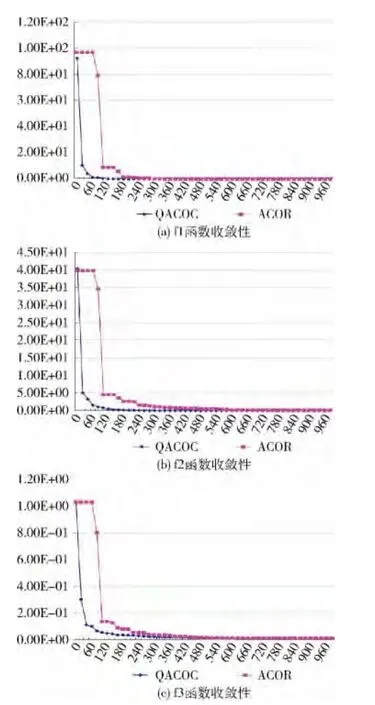
图6 两种算法的收敛情况

3.2 求解精度分析

对算法的求解精度进行比较，目的是为了研究算法的全局搜索性能，从而验证算法是否具有避免陷入局部最优解的控制能力。让QACOC和ACOR两种算法每次都运行足够长时间，然后对它们每次运行所获得的解进行统计分析，得出的结果见表2。其中α表示获得最优解0.0的次数，ω为20次解的平均值，Good为最佳解，Bad为最坏解。

对表2中数据进行分析可知，在简单的单极值函数f1上，QACOC和ACOR算法在20次运行过程中均能够获得最优解0.0。但在复杂的多极值函数上，两种算法的求解精度却相差较大。例如在f2函数上，QACOC算法20次都能获得最优解0.0，而ACOR算法只获得了18次最优解；而在f3函数上，QACOC算法能获得19次最优解，而ACOR算法仅获得最优解4次。

由表2可知，QACOC算法的求解精度相对于ACOR算法具良好的总体性能，耗费较小的计算成本便能获得更精确的解，表明其具有更好的全局搜索能力。实验结果表明，基于分布估计的量子信息素模型是一种高效合理的信息素控制方法。

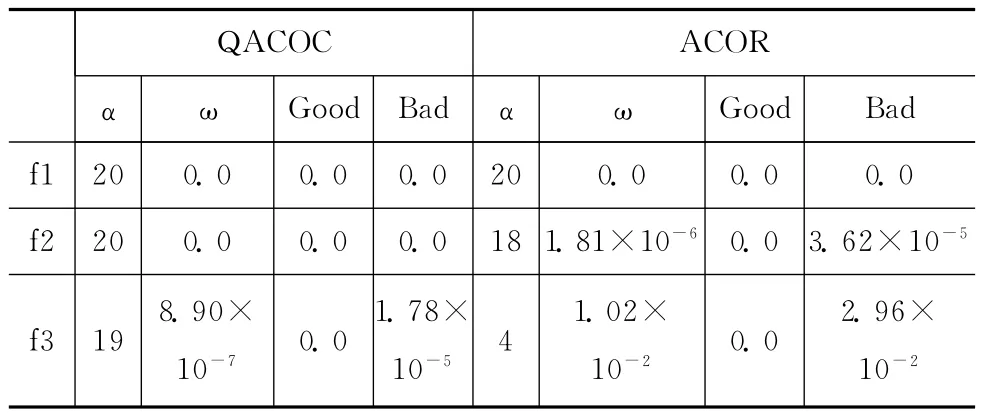
表2 求解精度对比

4 结束语

融合分布估计和量子态的叠加机制，本文提出了一种基于分布估计的量子信息素控制策略。新的信息素控制策略既具有分布估计算法的宏观优化特点，又具有量子态叠加机制的多样性。实验结果表明，量子态叠加特性和分布估计方法相结合的信息素控制策略可以有效避免蚁群算在法求解连续问题时使其陷入局部最优，提高了蚂蚁搜索的多样性和全局引导能力。新信息素模型的引入能够帮助蚁群算法对连续问题具有较好的优化能力，耗费较小的计算代价便可获得更精确的解。

［1］Toksari M Duran.Ant colony optimization for finding the global minimum［J］.Applied Mathematics and Computation，2006，126（1）:308－316.

［2］Socha K，Dorigo M.Ant colony optimization for continuous domains［J］.European Journal of Operational Research，2008，185（3）:1155－1173.

［3］LI Panchi，LI Shiyong.Quantum ant colony algorithm for continuous space optimization［J］.Control Theory ＆Applica－tions，2008，25（2）:237－241（in Chinese）.［李盼池，李士勇.求解连续空间优化问题的量子蚁群算法［J］.控制理论与应用，2008，25（2）:237－241.］

［4］CEN Yusen，XIONG Fangmin，ZENG Biqing.Ant colony algorithm based on new pheromone updated strategy［J］.Application Research of Computers，2010，27（6）:2080－2083（in Chinese）.［岑宇森，熊芳敏，曾碧卿.基于新型信息素更新策略的蚁群算法［J］.计算机应用研究，2010，27（6）:2080－2083.］

［5］ZHOU Shude，SUN Zengqi.A survey on estimation of distribution algorithms［J］.Acta Automatica Sinica，2007，33（2）:113－124（in Chinese）.［周树德，孙增圻.分布估计算法综述［J］.自动化学报，2007，33（2）:113－124.］

［6］Andre V Abs da Cruz，Marley M B R Vellasco，Marco Aurelio C Pacheco.Quantum－inspired evolutionary algorithm for numerical optimization［C］//IEEE Congress on Evolutionary Computation，Vancouver，2007:2630－2637.

［7］Yan W，Xiaoyue F，Yanxin H，et al.A novel quantum swarm evolutionary algorithm and its application［J］.Neurocomputing，2007，70（4－6）:633－640.

［8］LI Shiyong，LI Panchi.Quantum computing and quantum optimization algorithm［M］.Harbin:Harbin Industrial University Press，2009:108－116（in Chinese）.［李士勇，李盼池.量子计算与量子优化算法［M］.哈尔滨:哈尔滨工业大学大学出版社，2009:108－116.］

［9］Dorigo M，Birattari M，Stutzle T.Ant colony optimization:Artificial ants as a computational intelligence technique［J］.IEEE Computational Intelligence Magazine，2006（11）:28－39.

［10］Dorigo M，Stutzle T.Ant colony optimization［M］.ZHANG Jun，HU Xiaomin，LUO Xuyao，et al transl.Tsinghua University Press，2007:63－115（in Chinese）.［Dorigo M，Stutzle T.蚁群优化［M］.张军，胡晓敏，罗旭耀，等译.清华大学出版社，2007:63－115.］