基于滑动窗口聚类的时序关联规则挖掘方法

张忠林，周晓侠

（兰州交通大学电子与信息工程学院，甘肃兰州730070）

0 引 言

时间序列挖掘是指挖掘同一个时间序列内或者多个时间序列之间的依赖关系［1］。近年来，挖掘价格时间序列将来的变化趋势已经成为热点［2］。Agrawal等首次提出了关于时态关联规则的挖掘，并给出了序列模式的概念［3］。为了描述在关联规则中时间的变化特点，荣刚等提出动态关联规则的定义［4］；沈斌等对其进行了改进［5］，能更好地反映规则随时间变化的动态信息。对时间序列进行聚类能有效的提高挖掘关联规则的效率［6，7］，通过挖掘序列的趋势变化，可挖掘出更加实用的规则［8］。本文目的是如何在一个时间序列内发现类似“A发生后，B在时间T内紧跟着发生”这样的规则，或者是在多个时间序列中发现类似“A在时间序列S中发生后，B在时间序列Z中，在时间T内紧跟着发生”这样的规则，其中A，B是时间序列S或Z中的某种变化趋势。例如，在一段时间内，移动公司的通话拨入量达到高峰前，总会伴随一个低谷的出现。与以往的算法［9］不同之处是:根据时间序列随着时间的变化将呈现不同的变化趋势，且在特定时间段内某种趋势在时间序列中频繁发生，挖掘时序关联规则。

1 时间序列离散与聚类

考虑时间序列的时间有序性，本文利用滑动窗口机制对时间序列进行初步离散。再利用聚类算法K－Means对离散得到的子序列进行趋势聚类。并对相关参数作分析。

1.1 时间序列离散

假设存在时间序列S和宽度为w的滑动窗口，S＝｛x1，x2，x3，…，xn｝。现将S划分为N个长度为w的子序列Si，其中，N＝n－w＋1，Si＝｛xi，…，xi＋w－1｝。每划分得到一个子序列，滑动窗口向前滑动w个位置，则依次得到子序列S0，S1，S2，…，Sn－w。离散后得到的子序列集合记为W（S），W（S）＝｛［ID，Si］｜0≤ID＜n－w＋1，0≤i＜n－w＋1｝，其中ID表示子序列编号。

定义1 形状:子序列的变化趋势被看作子序列所具有的一种形状。

例如:假设存在长度为4的子序列Si和Sj，Si的形状为先上升，再下降，后又上升，Sj的形状为先上升，再下降，后又持平。

1.2 K－Means聚类

聚类分析是分析时间序列的一种常用方法，现有的聚类算法多是根据相似性对事物进行聚类。最佳聚类结果应该是类内距小，内间距大。

离散后的子序列Si具有不同或相同的形状，因此可利用K－Means根据其形状相似性将W（S）中的所有子序列分为k个类，将具有相同形状的子序列分为一类，即C0，C1，C2，…，Ck－1。将聚类得到的k个类用k个布尔变量标志，则可得到趋势序列D（S），D（S）＝｛［ID，ai］｜0≤ID＜nw＋1，0≤i＜k｝，其中，ID为子序列编号，ai为布尔变量，即编号为ID的子序列属于标志名为ai的类。

在聚类的过程具有相同形状的子序列Si和Sj，因其取值区间相差太大而被误分在不同的类中。因此，在对子序列进行聚类前需要对其进行标准化，使得具有相同形状的子序列处在近似的取值区间。存在子序列Si＝｛xi，…，xi＋w－1｝，可采用以下两种方法对xi进行标准化:

（1）均值标准化

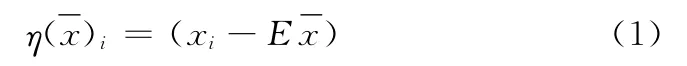
（2）方差标准化

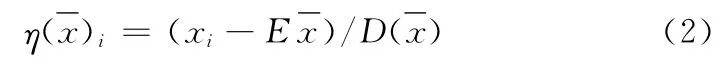
1.3 参数分析

数据离散的过程中主要涉及到两个参数，即w（滑动窗口的宽度）和k（聚类数）。滑动窗口宽度w值的选择多是根据用户需求以及预处理数据的条件，可采用多粒度时间进行测试。聚类数k的值不能太大，否则将产生太多的形状，从而生成过多的规则。k值也不能太小，否则一个形状与另一个形状相隔太远。可利用用户对挖掘出的规则的兴趣度进一步确定w和k的值。

2 时序关联规则

Apriori算法是基于事物数据库进行规则挖掘，每个事物中的元素按字典顺序排列，这种排列破坏了最初的时态关系。因此，为了挖掘出更有效的规则，首先，在趋势序列中寻找频繁特征，其次，利用Apriori算法生成频繁高项集，最后发现时序关联规则。

2.1 时间序列

存在趋势序列D（S）＝｛［ID，ai］｜0≤ID＜n－w＋1，0≤i＜k｝。本文的目的是发现类似这样的规则，即在一个时间序列S中，A发生后，在时间T内，B紧跟着发生，其中A，B∈D（S）。

在关联规则的基础上，对其相关定义进行补充和重新定义，具体定义如下:

定义2 A的绝对支持度:A在趋势序列D（S）中出现的次数F（A），即

定义3 A的相对支持度

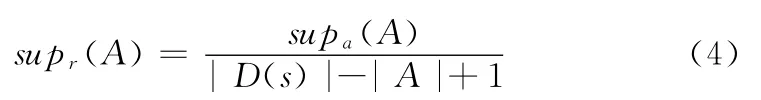
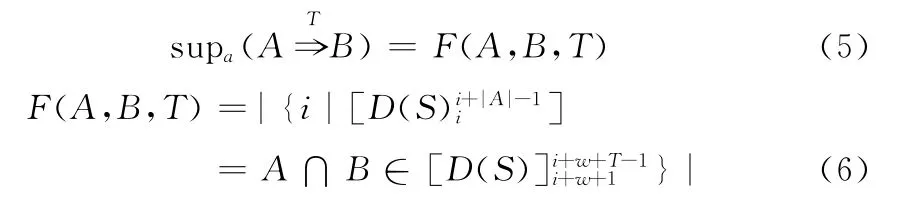
其中，0≤i＜｜D（S）｜－｜AB｜。

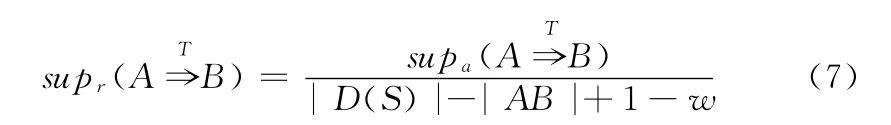
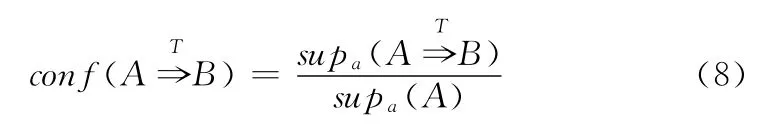
随着时间序列数据库的数据增多，D（S）的长度变大，将会产生越来越多的关联规则。恰当的最小支持度和最小置信度将能够有效地减少冗余规则的生成，但是仍然需要办法将用户感兴趣的规则和不感兴趣的规则进行区分。因此本文采用Smyth提出的J－measure准则对满足支持度阈值和置信度阈值的规则按J值得大小进行排序，J值较大的规则将是用户更感兴趣的规则。设规则的J值为J（BT；A）式中:P（A）——形状A在D（S）中出现的概率。p（BT）——B在D（S）中出现的概率。p（BT｜A）——在D（S）中A发生后，间隔小于T时间后B发生的概率。

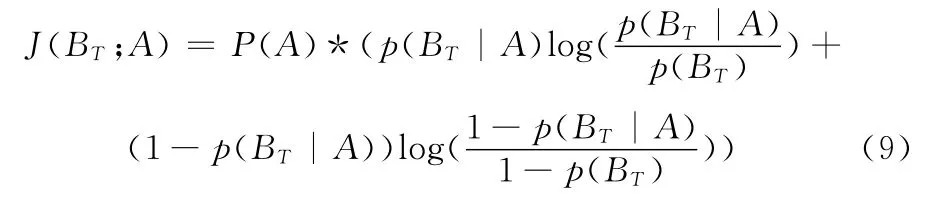
2.2 多时间序列

特定时间内的规则不仅可以存在一个时间序列中，也可以存在多个时间序列中，即时间序列S中A出现后，在时间T内，时间序列Z中B紧跟着出现，该规则记为B（A∈D（S），B∈D（Z））。或者是A1，A2，A3，…，Ak在时间V内发生，紧跟着B在时间T内发生，该规则记为A1，A2，…，其中（A1，A2，A3，…，Ak∈D（S），B∈D（Z））。

根据时间序列的相关定义得到多时间序列中时序关联规则的支持度和置信度的表现形式如下

推论1 A1，的绝对支持度

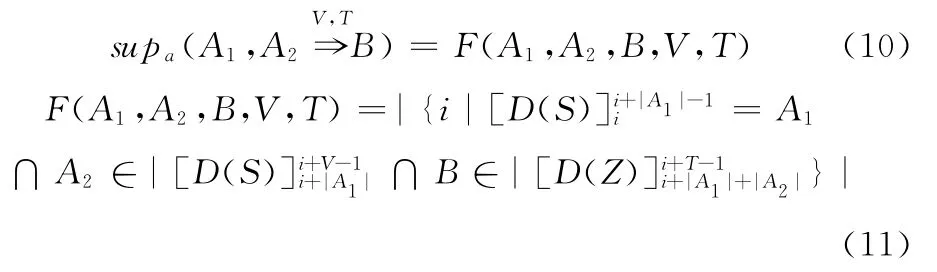
推论2 A1，的相对支持度

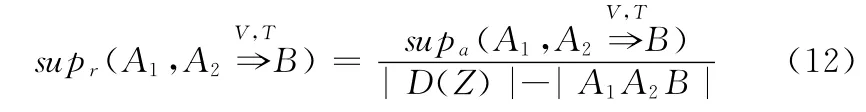
推论3 A1，的置信度

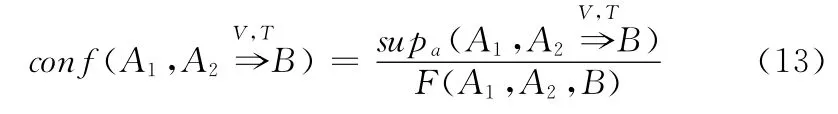
多个时间序列中挖掘特定时间内的规则也可利用式（9）对规则进行排序，从而得到用户感兴趣的规则。规则A1，的J值为

3 算法描述

本文提出的基于滑动窗口聚类的时序关联规则挖掘方法可用于一个时间序列或多个时间序列，其算法描述如下。

（1）时间序列算法描述

输入:w，k，S，min＿sup，min－conf，T，min＿J

//输入滑动窗口宽度w，聚类数k，时间序列

//S，最小支持度min＿sup，最小置信度

//min－conf，最小J值min＿J，预设时间段//T

输出:Rules

1）all＿SubSequence＝Generate＿SubSequence（S，w）；

//利用滑动窗口初步离散化S，all＿SubSequence

//存储所有的子序列

2）W（S）＝Normal＿SubSequence（all＿SubSequence，w）；

//利用式（1）对all＿SubSequence进行标准化，结//果存储在W（S）

3）Num＝W（S）.Length；//Num为子序列的数目

4）K－Means（k，W（S））；//调用K－Means算法聚类得//到C0，C1，C2，…，Ck－1

5）for j＝0 to k－1

Cj→j；//利用布尔变量j＝0，1，2，…，k－1

//标志每个类Cj

6）for i＝0 to n－w

for j＝0 to k－1

if（W（S）i∈Cj））//判断每个子序列的形状

then D（S）i＝［i，j］；//生成趋势序列

7）FrequenctOneSets＝Generate＿FrequentOne（D（S））；

//利用定义2产生频繁特征

8）Frequenct LowSets＝FrequenctOneSets；

9）GenerateHighFrequenct（Frequenct LowSets，T）

//生成频繁高项集

10）If（supA∪B≥min＿sup and confA∪B≥min＿conf）

//A，B∈D（S），supA∪B为A∪B的支持度，confA∪B

//为A∪B的置信度

11）for each rule riin R do

Jri＝J（BT；A）；//利用J－measure准则求J值

12）If（Jri≥min＿J）

insert riinto Rules；

13）return Rules；

（2）多时间序列挖掘算法描述如下:

1）利用本文提出的算法分别挖掘出时间序列S和时间序列Z的频繁项集。

时间序列S的频繁1项集I（S）1＝｛Ai｝，（0≤i＜k，Ai∈D（S）），频繁2项集I（S）2＝｛Ai×Aj｝，（0≤i＜k，i＜j＜k，Ai，Aj∈D（S）），频繁3项集I（S）3＝｛Ai×Aj×Am｝，（0≤i＜k，i＜j＜k，j＜m＜k，Ai，Aj，Am∈D（S）），以及其它高频繁项集。时间序列Z的频繁1项集为I（Z）1＝｛Bi｝，（0≤i＜k，Bi∈D（Z））。

2）将时间序列S的频繁项集与时间序列Z的频繁1项集进行连接，即I（S）i×I（Z）1，（1≤i≤n－w＋1）。若I（S）i×I（Z）1的支持度大于预设的最小支持度阈值，则得到关于序列S和序列Z的高频繁项集。剩余工作类似于一般时间序列规则挖掘。

4 实验分析

本文实验用的数据来源于文献［10］中的示例数据。分别是上海（SH）300天内每天的综指变化序列，以及深圳（SZ）300天内每天的成指变化序列。则有序列SH和SZ，其长度均为300。

实验目的:首先，利用本文所提出的算法针对序列SH发现用户感兴趣的规则，并对规则进行分析。其次，当算法中的参数发生变化时，分析挖掘结果。最后，利用本文提出的算法针对序列SH和序列SZ挖掘多时间序列中特定时间段内的规则。

4.1 时间序列规则挖掘

设w＝10，k＝7，T＝20，最小支持度为0.03，最小置信度为0.4，利用本文提出的算法进行规则挖掘。

（1）利用滑动窗口机制对序列SH（记为S）初步离散后，再标准化得到序列W（S）＝｛［ID，Si］｜0≤i＜n－w＋1｝。

（2）利用K－Means聚类方法对W（S）进行聚类，得到7种聚类结果，C0，C1，C2，C3，C4，C5，C6，即将序列的变化趋势分为7种形状。

（3）利用布尔变量“0”，“1”，“2”，“3”，“4”，“5”，“6”标志每一种形状，即“0”代表C0类形状，“1”代表C1类形状等。将W（S）中的子序列与其所属形状相对应，得到趋势序列D（S），D（S）＝｛i，j｝，其中i为序列编号，j为布尔变量。D（S）＝｛［0，3］，［1，3］，［2，6］，［3，6］，［4，1］，［5，1］，［6，1］，［7，1］，［8，1］，［9，6］，［10，6］，［11，0］，［12，0］，［13，0］，［14，0］，［15，0］，［16，0］，［17，0］，［18，2］，［19，2］，［20，1］，［21，1］，［22，4］，［23，4］，［24，3］，［25，3］，［26，3］，［27，3］，［28，3］，［29，3］，［30，3］，［31，3］，［32，3］，［33，3］，［34，3］，［35，3］，［36，1］，［37，6］，［38，6］，［39，6］，［40，6］，［41，6］，［42，6］，［43，0］，［44，0］，［45，0］，［46，0］，［47，0］，［48，0］，［49，0］，［50，0］，［51，2］，［52，2］，［53，2］，［54，1］，［55，1］，［56，1］，［57，6］，［58，6］，［59，6］，［60，6］，［61，0］，［62，0］，［63，0］，［64，0］，［65，2］，［66，1］，［67，4］，［68，4］，［69，4］，［70，5］，［71，5］，［72，5］，［73，5］，［74，5］，［75，5］，［76，3］，［77，3］，［78，6］，［79，0］，［80，0］，［81，2］，［82，2］，［83，2］，［84，1］，［85，6］，［86，1］，［87，0］，［88，0］，［89，0］，［90，2］，［91，1］，［92，4］，［93，4］，［94，3］，［95，3］，［96，3］，［100，3］，［101，3］，［102，3］，［103，4］，［104，4］，［105，4］，［106，3］，［107，3］，［108，6］，［109，0］，［110，0］，［111，0］，［112，2］，［113，2］，［114，2］，［115，1］，［116，4］，［117，4］，［118，3］，［119，3］，［120，3］，［121，3］，［123，6］，［124，0］，［125，0］，［126，0］，［127，0］，［128，0］，［129，0］，［130，2］，［131，4］，［132，4］，［133，4］，［134，4］，［135，3］，［136，3］，［137，3］，［138，6］，［139，0］，［140，0］，［141，0］，［142，0］，［143，0］，［144，0］，［145，0］，［146，0］，［147，0］，［148，0］，［149，2］，［150，2］，［151，2］，［152，2］，［153，0］，［154，0］，［155，0］，［156，0］，［157，0］，［158，0］，［159，1］，［160，1］，［161，4］，［162，3］，［163，3］，［164，6］，［165，0］，［166，6］，［167，6］，［168，2］，［169，0］，［170，0］，［171，0］，［172，0］，［173，0］，［174，1］，［175，1］，［176，1］，［177，1］，［178，1］，［179，6］，［180，6］，［181，6］，［182，6］，［190，0］，［191，0］，［192，1］，［193，1］，［194，1］，［195，1］，［196，6］，［197，6］，［198，6］，［199，6］，［200，1］，［201，1］，［202，1］，［203，1］，［204，1］，［205，6］，［206，0］，［207，0］，［208，0］，［209，2］，［210，2］，［211，2］，［212，2］，［213，1］，［214，4］，［215，4］，［216，5］，［217，5］，［218，5］，［219，3］，［220，3］，［221，6］，［222，0］，［223，2］，［224，2］，［225，2］，［226，1］，［227，4］，［228，3］，［229，4］，［230，4］，［231，4］，［232，5］，［233，5］，［234，5］，［235，5］，［236，5］，［237，3］，［238，3］，［239，6］，［240，0］，［241，2］，［242，1］，［243，4］，［244，4］，［245，4］，［246，3］，［247，3］，［248，3］，［249，3］，［250，1］，［251，6］，［252，6］，［253，0］，［254，0］，［255，0］，［256，2］，［257，2］，［258，4］，［259，4］，［260，4］，［261，5］，［262，5］，［263，4］，［264，4］，［265，3］，［267，3］，［268，3］，［269，6］，［270，6］，［271，4］，［272，4］，［273，2］，［274，4］，［275，4］，［276，4］，［277，4］，［278，3］，［279，3］，［280，3］，［281，6］，［282，0］，［283，0］，［284，0］，［285，0］，［286，6］，［287，6］，［288，2］，［289，2］｝。

（4）对D（S）进行规则挖掘。挖掘得到的规则输出形式为:［支持度，置信度，J］。t的含义是:A发生后，B相隔t－1（t≤T）天发生。生成规则如下:

当t＝3时，有规则:

02［0.0395，0.3538，0.0496］

24［0.0206，0.4138，0.0249］

45［0.0223，0.3514，0.0286］

当t＝4时，有规则:

16［0.0258，0.3750，0.0284］

24［0.0206，0.4138，0.0249］

当t＝13时，有规则:

23［0.0189，0.3793，0.0146］

当t＝18时，有规则:

24［0.0189，0.3793，0.0210］

当t＝19时，有规则:

24［0.0206，0.4138，0.0249］

（5）按J值对规则进行排序。根据J－measure准则，J值越大则其忠实度越高，更有可能是用户感兴趣的规则。因此，认为规则（t＝3）最有可能为用户感兴趣的。

（6）遍历序列D（S），查询形状“0”和“2”在3天时间内第一次相继发生时对应的序列编号，得到规则S19（t＝3），即若模式S16发生后，最多在20天内（实际为3天）模式S19紧跟着发生。如图1（a）所示，上海综指在持续了约10天的锐减之后（模式S16），在20天内，上海综指肯定将会出现先持续下降一周再上升的概率为0.0395（模式S19）。表1列出了在w，k取不同值的情况下，具有较高J值的规则及其支持度、置信度和J值等。

如表1所示，当J值均较高，聚类数发生微小变化时，滑动窗口的宽度w＝10和w＝20的置信度小于w＝13和w＝16置信度。由此说明，滑动窗口的宽度不能太小，否则趋势特征过于单调；同时，滑动窗口的宽度也不能太大，否则容易忽略更有意义的规则。因此，w的选择应根据具体需求以及已挖掘到的规则的J值、置信度和支持度。

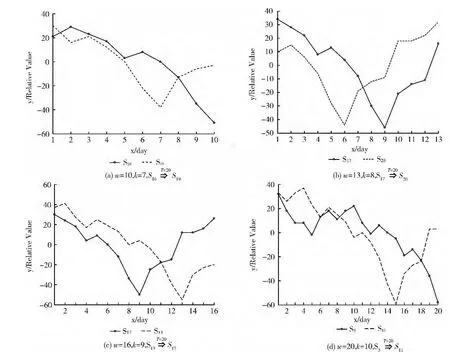
图1 参数w，k取不同值时的规则变化趋势

4.2 多时间序列规则挖掘

通过时间序列SH（记为S）和时间序列SZ（记为Z）进行多时间序列规则挖掘。

当w＝10，k＝7，T＝20，V＝10，最小支持度为0.03，最小置信度为0.4时挖掘出的J值较高的规则为支持度为0.0344，置信度为0.3636，J值为0.0102。图2为的规则趋势图。

如图2所示，上海综指出现持续10天的下降之后（模式S16），紧跟着在10天内，（模式S19）出现先下降一周后上升的趋势。相应的，深圳成指在上海成指发生了如上变化后，在20天内（模式Z13）肯定会出现先缓慢下降到出现明显的下降趋势的概率是0.0344。

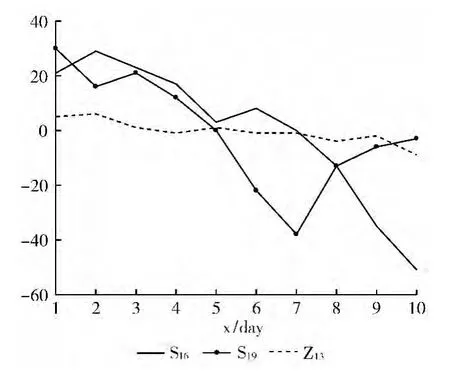
图2 w＝10，k＝7，（S16，S19）的变化趋势

实验结果表明:①根据用户的要求，对相关参数进行弹性设置可挖掘出用户感兴趣的规则；②参数w，k发生局部变化时对挖掘出的规则影响不大；③挖掘出的规则可用于做短期的预测或决策；④随着w的变化，可预测长度随之伸缩。传统的时间序列挖掘算法主要针对多个时间序列中特定时间段内单个趋势状态进行挖掘，对于规则的趋势变化反映不全面，而本文提出的算法可以反应多个状态。文献［9］所提算法基于事物数据库挖掘，每个事物的元素按字典顺序，虽能提高整体的挖掘效率，但是破坏了基础的时态关系，而本文中提出的算法在进行规则挖掘前，去除了关联规则挖掘方法基于事物数据库挖掘的约束。

5 结束语

本文给出了特定时间段内时序关联规则的相关定义，并提出了基于滑动窗口聚类的时序关联规则挖掘方法。最后通过实验证明该方法不仅能使用户发现更有价值的规则，且能反映规则在局部时间内的变化趋势，从而指导用户做短期的预测或决策。例如，利用该方法挖掘股票、气象等特定时间段内的变化规则。

本文仍存在一些不足，需要进一步的研究。本文根据预设的支持度阈值和置信度阈值进行规则筛选，可能会忽略一些潜在的规则。类似规则因其支持度和置信度在全局上小于预设的支持度阈值和置信度阈值而被忽略，但其在局部时间上具有一定的显著性。对于这些规则的挖掘仍需进一步的研究。

［1］Pradhan G N.Association rule mining in multiple，multidimensional time series medical data［C］//Proceedings of the IEEE International Conference on Multimedia and Expo，2009:1720－1723.

［2］QIN Liping，BAI Mei.Predicting trend in futures prices time series using a new association rules algorithm［C］//Proceedings of the 16th IEEE International Conference on Management Science ＆Engineering，2009:1511－1517.

［3］Agrawal R，Srikant R.Mining sequential patterns［C］//Proceedings of the 11th IEEE International Conference on Data Engineering，1995:3－14.

［4］RONG Gang，LIU Jinfeng，GU Haijie.Mining dynamic association rules in databases［J］.Control Theory and Applications，2007，24（1）:129－133（in Chinese）.［荣冈，刘进锋，顾海杰.数据库中动态关联规则的挖掘［J］.控制理论与应用，2007，24（1）:129－133.］

［5］SHEN Bin，YAO Min.A new kind of dynamic association rule and its mining algorithms［J］.Control and Decision，2009，24（9）:1310－1315（in Chinese）.［沈斌，姚敏.一种新的动态关联规则及其挖掘算法［J］.控制与决策，2009，24（9）:1310－1315.］

［6］Thanawin R.Time series epenthesis:Clustering time series streams requires ignoring some data［C］//Proceedings of the 11th International Conference on Data Mining，2011:547－556.

［7］Liwei L，Qiangjiang J.A hidden Markov model－based KMeans time series clustering algorithm［C］//Proceedings of IEEE International Conference on Intelligent Computing and Intelligent Systems，2010:135－138.

［8］ZHANG Zhonglin，ZENG Qingfei.Method of data tendency measure mining in dynamic association rules［J］.Journal of Computer Applications，2012，32（1）:196－198（in Chinese）.［张忠林，曾庆飞.动态关联规则的趋势度挖掘方法［J］.计算机应用，2012，32（1）:196－198.］

［9］ZHANG Lingjie，XU Weixiang.Association rules mining algorithm based on temporal constraint［J］.Computer Engineering，2012，38（5）:50－51（in Chinese）.［张令杰，徐伟祥.基于时态约束的关联规则挖掘算法［J］.计算机工程，2012，38（5）:50－51.］

［10］ZHANG Xiaodong.Econometrics［M］.3rd ed.Beijing:Chinese People’s Publishing House，2008（in Chinese）.［张晓峒.计量统计学［M］.3版.北京:中国人民出版社，2008.］