地形图测量精度对土石方计算的影响分析

胡吉伦，程正逢，徐 辉

(中南电力设计院，湖北 武汉 430071)

地形图测量精度对土石方计算的影响分析

胡吉伦，程正逢，徐 辉

(中南电力设计院，湖北 武汉 430071)

从满足土石方工程量计算精度要求出发，分析现行不同行业测量规程在地形图测量上的异同点，对全站仪三角高程测量的高差精度进行分析，提出地形点注记高程精度指标和地形点注记间距要求。同时对高程点高程精度对土石方计算的影响进行了分析。

高程点注记间距；测点高差精度；土石方工程量。

1 概述

在电力工程(变电站、发电厂)勘测设计过程中，如何为设计提供准确可靠的测量数据进行土石方工程量计算，是个多年来困扰测量人员的问题。随着经济的发展、工程成本的提高和工程预算制度的严格执行，设计计算土石方与实际土石方不合的矛盾日益突出。

现今常用的土方计算方法有方格法、断面法、等高线法、数字地面模型法(DTM)、三角网法(TIN)，任何一种方法实际精度主要由原始数据的采集误差和高程内插误差两方面决定。数据采集误差来自测点设备误差、测量误差等，而高程内插误差取决于测点密度和点位位置。

为进一步做好设计服务，满足土石方计算误差要求，使工程量计算更科学合理，需要对野外测点高程精度、测点的密度进行探讨，找出科学合理的解决方案，满足业主不断提高的要求。

2 现行测量标准

目前厂区电力工程测量使用的测量规范是：《火力发电厂工程测量技术规程》(DL/T 5001－2004)行业标准，《水利水电工程测量规范》(SL 197－97)行业标准，《工程测量规范》(GB 50026－2007)国家标准，《1:500 1:1000 1:2000外业数字测图技术规程》(GB/T 14912－2005)国家标准。在这些规范中，对于地形图测绘精度，没有提出要满足施工土石方工程量计算的要求，但业主对计算土石方工程量有要求(如有的要求“土石方平衡工程量误差不超过±5%”等)，这就对地形测量提出了挑战。地形测量内容包括：地面地形地貌、地物信息和地下信息等。设计使用地形图，一方面进行总平面布置，另一方面计算土石方工程量。而土石方工程量的计算，与地形图高程点注记间距及精度、等高线或插求点有关。

2.1 高程点注记间距要求

对于高程点注记间距，各工程标准的要求见表1。

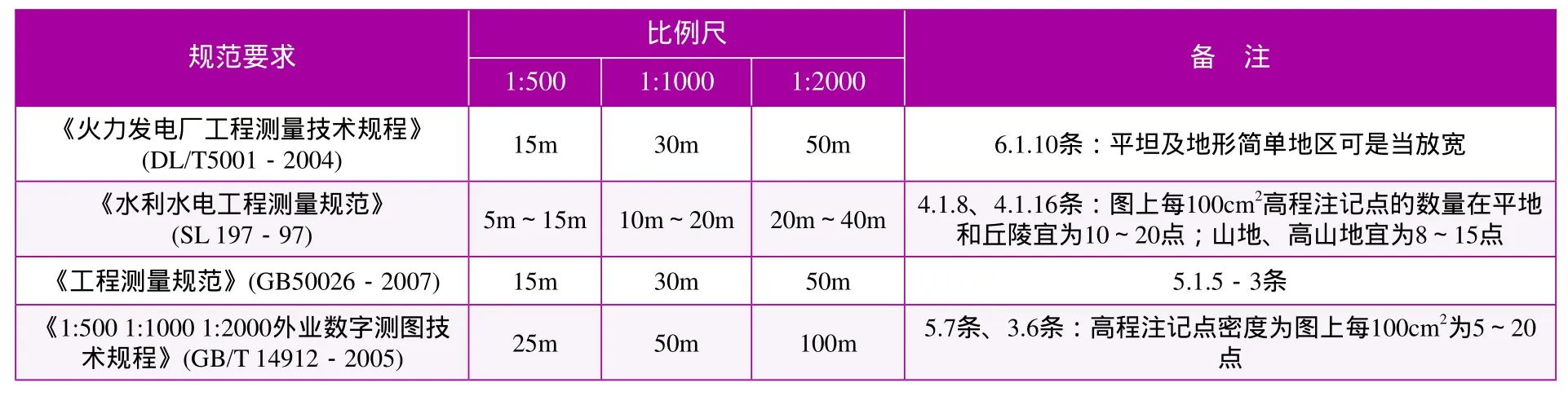
表1 几种工程标准对测点密度要求

2.2 高程注记点精度要求

对于高程注记点的精度，各工程标准的要求见表2。

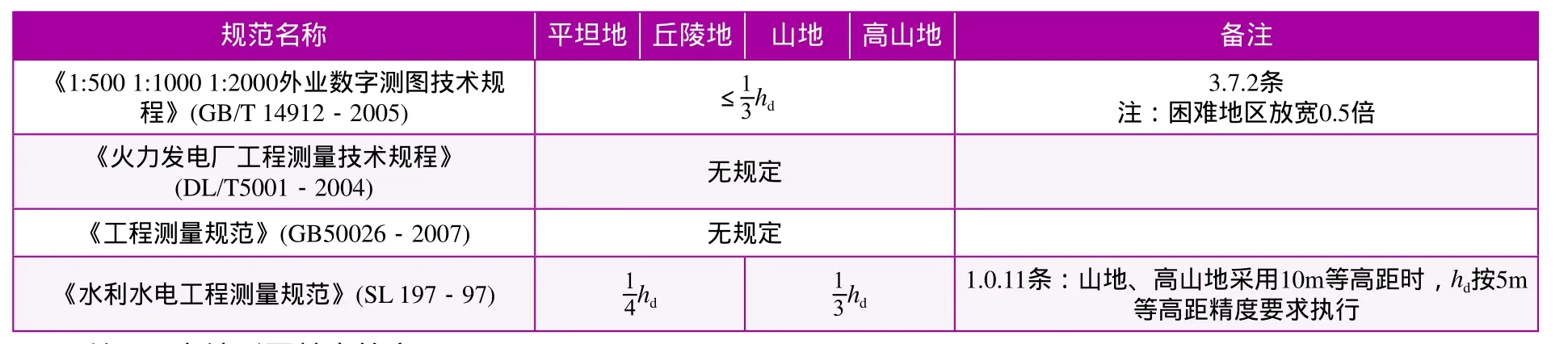
表2 几种工程标准对高程注记点高程精度要求

2.3 等高线或插求点高程精度要求

对于等高线或插求点高程精度，各工程标准的要求见表3。

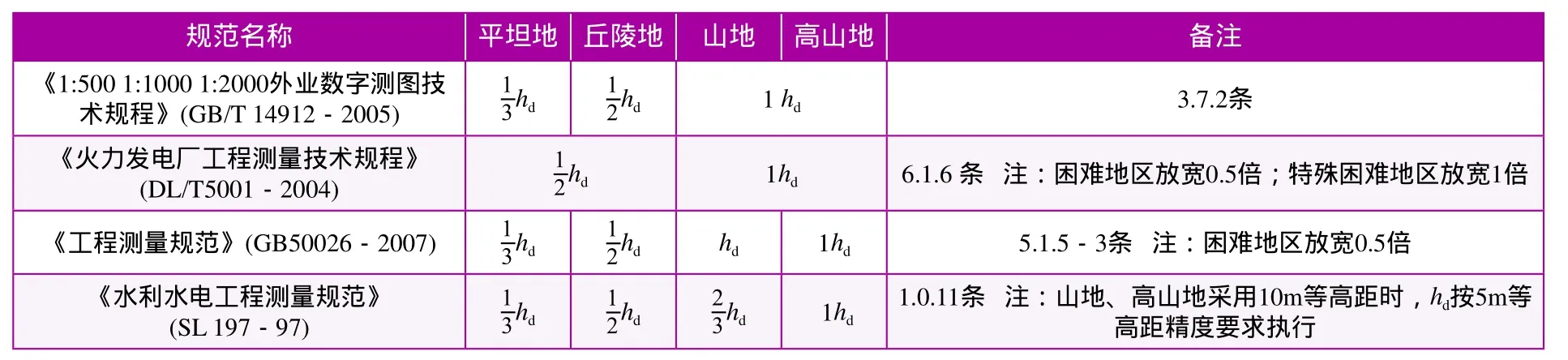
表3 几种工程标准对等高线或插求点高程精度要求

2.4 几种工程标准的比较

(1)测点密度方面，《工程测量规范》与《火力发电厂工程测量技术规程》注记点密度相同，《水利水电工程测量规范》注记点密度最高，《1:500 1:1000 1:2000外业数字测图技术规程》注记点密度最低。

(2)高程注记点精度方面，《工程测量规范》与《火力发电厂工程测量技术规程》无规定，《水利水电工程测量规范》要求高程注记点精度高于《1:500 1:1000 1:2000外业数字测图技术规程》。

(3)等高线或插求点高程精度方面，《水利水电工程测量规范》要求高于《火力发电厂工程测量技术规程》和《1:500 1:1000 1:2000外业数字测图技术规程》，与《工程测量规范》要求相同。

3 全站仪采集高程点精度分析

从以上规范中可以看出，《水利水电工程测量规范》提出了高程注记点精度和较高的密度，比较好地规定出地形图测图精度。

由于土石方工程量与地形图高程注记点精度和密度有关，而高程注记点精度与全站仪三角高程测量精度相关。下面对三角高程测量高差精度进行分析：

全站仪三角高程测量高差计算公式：

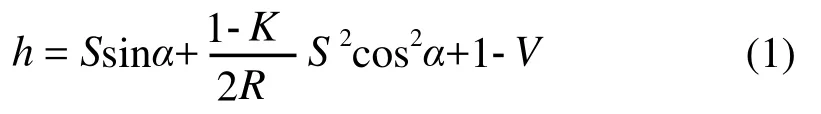
式中：h为高差；S为斜距；α为垂直角；I为仪器高；V为觇标高；K为大气折光改正；R为地球半径。

根据误差传播定律, 忽略微小项，得到高差中误差为：

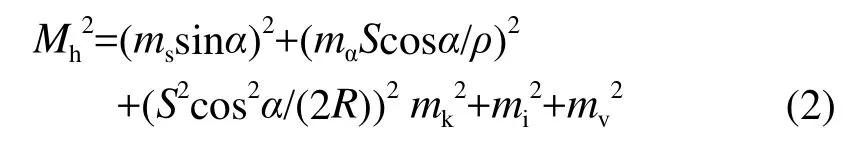
式(2)中，又因mk较小(一般为±0.03mm～0.05mm)，忽略，式(2)简化为：

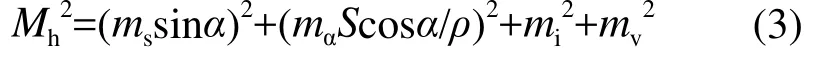
在全站仪地形图测量中，取ms=±14mm(取自《工程测量规范》全站仪测图要求，距离按700m计算)

mα=±18″(取自《工程测量规范》图根电磁波测距三角高程的主要技术要求)

其他取值为：

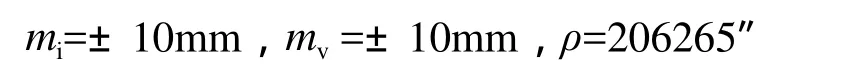
按式(3)计算，垂直角和距离对高差的影响见表4。

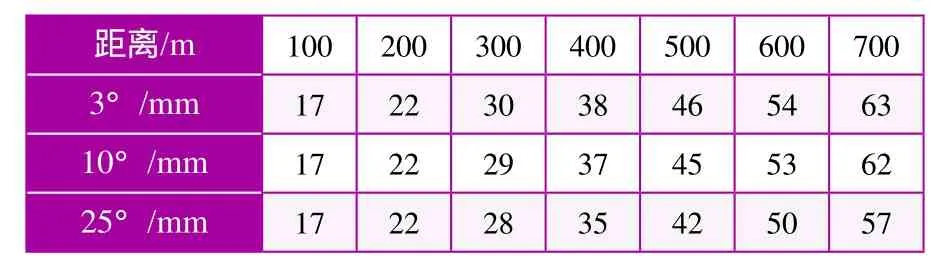
表4 垂直角和距离对地形点高差中误差影响

根据《工程测量规范》，对于1:2000地形图，全站仪测量地形点最大距离为700m，则平地、丘陵地形的地形点高差中误差为63mm。图根点高程中误差不大于基本等高距的1/10，以基本等高距为1m计算，则有：

可以看出，测点高程误差主要是测站点高程误差。

取测点高差限差为±0.13m，测点高程限差为±0.3m。

从表4可知，垂直角对高差误差的影响不明显，距离影响明显。在野外工作中，提高测站点高程精度将大大提高地形图测点精度。

(1)除测点误差外，在地形图测量过程中，有些人为因素直接影响土石方工程量计算精度，如：测点点位不准，地形地物取舍不当等。因此，在野外测量过程中，测量人员需要注意如下事项：

①持镜员应进行岗前培训，地形图测量立点时，棱镜杆不应插入地下，应立于测点地面。

②地形地物的取舍应满足规范要求，根据电力工程地形图测量的特点，按照规范要求进行施测。

③测点应能反映地形的变化，如：坡度变化处、坎上坎下、沟底等，在测量稻田、旱地时，点位不应立在田、地中间的厢沟下面，应立在地台上面，并能反映田、地的地面高度。

()总结不同规范的要求，结合工作实际，我们认为目前地形图测量建议补充内容如下：

①地形点相对于测站点的高差限差为±0.15m；地形点高程限差为±0.3m。

②大比例尺地形图测点密度见表5。

表5 地形点点位间距 (单位：m)

4 高程点精度对土方量计算的影响

4.1 采用不规则三角网计算土石方量的方法

不规则三角网(Triangulated Irregular Network，TIN)指将按地形特征采集的点按一定规则连接成覆盖整个区域且互不重叠的连续三角形。TIN能较好地顾及地貌特征点、线，表示复杂的地形表面比矩形格网精确。我们将根据地形起伏变化的复杂性来确定采样点的密度和采样点的位置，从而可以避免地形平坦时的数据冗余，又能按地形特征点较好地逼近地形表面。在计算填方和挖方量的过程中，首先根据在挖前和挖后的地面特征点建立不规则三角网。在建立好的不规则三角网中，其每一个基本单元的核心是组成不规则三角形的三个顶点的三维坐标；从每个挖前三角形的三个顶点竖直向下引出三条直线，直到与挖后的地表面的三角网相交，便形成许多的三棱柱，这时整个区域的土石方地形便形成了由许多连续但不可微分的三棱柱组成的集合。分别计算出每个三棱柱的体积，所有的三棱柱体积之和便是整个区域的土石方量。

具体见图1：

现假设，面ABC为挖前地表面TIN中的三角形，面DEF为挖后地表面上的三角形面，面A1B1C1为上下表面在水平面上的投影；点A、B、C为测区内挖前地表面的特征点，点D、E、F为测区内挖后地表面上的地形点，其三维坐标(X，Y，H)已知。

首先令：

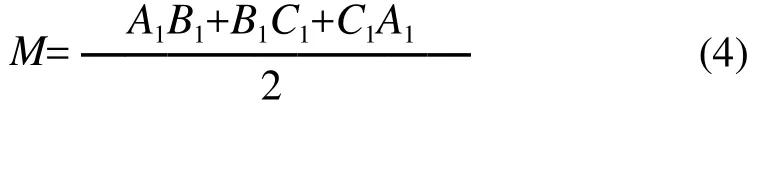
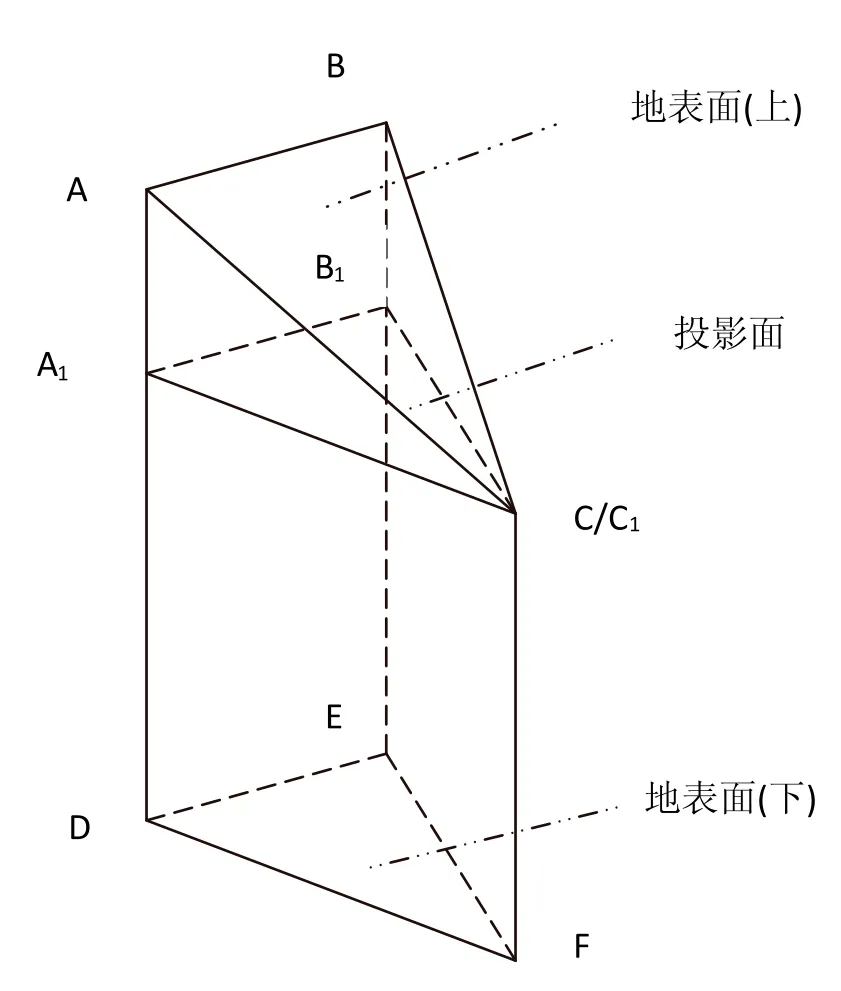
图1 不规则三角网计算土石方量示意图

则投影面的面积为：

其中A1B1、B1C1、C1A1、AD、BE、CF长度可由三角形几何关系求得，图1为三棱柱示意图。这样便求出了一个三棱柱的体积为V1；假设整个区域是由n个连续但不可微分的三棱柱组成，则整个区域的土石方量为：

式(7)中V1为各个不规则的三棱柱的体积。

4.2 高程点误差对采用TIN计算土石方量的影响分析

由上面的计算公式可以看出，单个三棱柱的体积与上表面在水平面上的投影面积、三角形挖前挖后的顶点高差之和相关，计算区域内的TIN由离散高程点按德劳内法则组成，离散点的分布决定了三角形的分布，对于分布一定的TIN来说，决定其土石方计算精度的就是三角形顶点高差之和。仅考虑高程点测量误差的影响，将每一个三角形面积看作一个常数，以挖方为例说明高程点高程误差对土石方量计算的影响。

假设所有高程为同样的方法测得，则高程点具有同样的高程精度，假设其高程误差为h。AD为A点高程减去挖方后的设计高程值，设计高程值为常量，则AD的误差也为h，同理BE、CF的误差也为h，将h值代入公式(6)，则：

则有

为了明确高程点的高程误差对土方量计算误差的影响程度，按以下方法进行了模拟计算：以一定面积的外业采集高程点作为理论数据，将高程点高程误差分别按+0.1m、+0.2m、+0.3m进行假设，计算的挖方量及高程误差影响比例见表6。

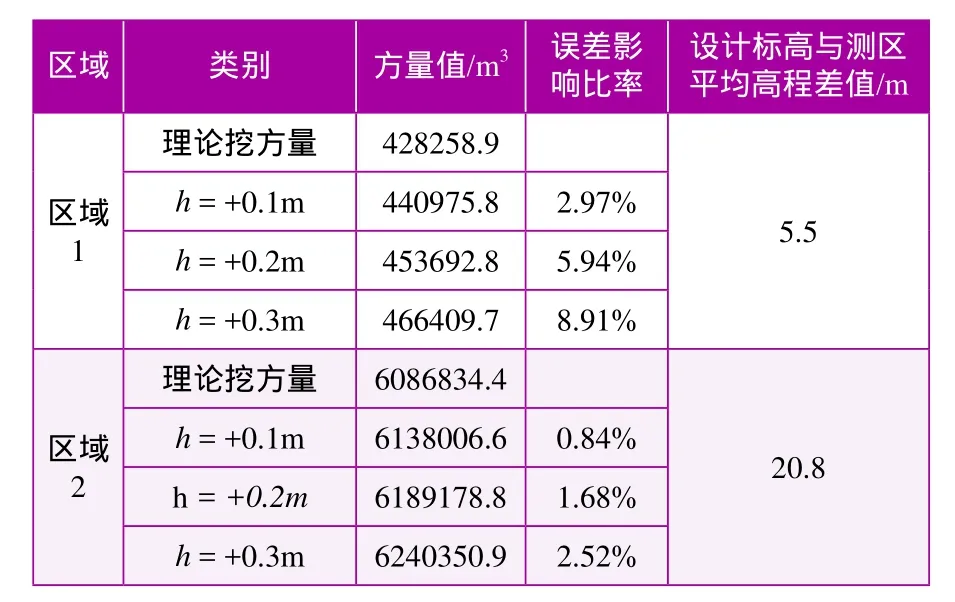
表6 高程误差对挖方量的影响计算

由表6可以看出，高程点的高程误差直接影响土方量计算的精度。

在实际的计算过程中，计算区域挖方体积只能依靠有限的三棱柱来模拟计算，为了尽可能提高区域体积计算的精度，有限的三棱柱的上表面三角形所代表的平面必须尽可能地接近地面实际情况，最大程度地模拟地面起伏变化，因此区域内构造TIN的高程点还要分布均匀，且具有足够多的地形地貌特征点。

如何确定土石方开挖平均高差与测点精度关系，《水电水利工程施工测量规范》(DL/T 5173－2012)7.6.10规定“对同一区域土石方挖填工程量进行两次独立测量计算的土方量差值不超过7%或石方量差值不超过5%时，可取其平均值作为最后值。”，《水利水电工程施工测量规范》(SL 52－93)5.3.15规定“两次独立测量同一区域的开挖工程量其差值小于5%(岩石)和7%(土方)时，可取中数(或协商确定)作为最后值。”，结合表6，我们可以推算出挖方平均高差与测点精度关系。

我们假设计算挖方高差误差与测点高程误差相同。

设 M1为第一次测量工程量；M2为第二次测量工程量；S为挖方平均面积；ΔH为挖方平均高差；M为挖方平均工程量。

则工程量

2次工程量计算差值

由于每次测量均有误差，对(1)、(2)式微分，按误差传播定律有

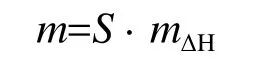
(18)式为挖方平均高差与高差精度的关系。

平均挖方高差与测量高差误差关系见表7。站点的高差限差为0.15m，点的密度按表5要求执行。从我们使用测量仪器精度看，结合目前测绘工作现状，对于地形点高差限差取0.15m，是可以满足的。

表7 平均挖方高差与测量高差误差关系 (单位：m)

从管理角度上看，在进行测量交桩过程中，需要使用测量仪器对现场关键地形点进行检测，并将测量数据提交给监理和施工单位，以减少施工过程中施工单位提出土石方工程量不符合的矛盾。

随着业主精细化管理的提高，对设计、施工管理日益细化，经济指标量化，对土石方工程量计算会提出更高要求。这对我们测量人员是个新的挑战，也为测量技术的发展提出了新的课题。

由于假设计算挖方高差误差与测点高程误差相同，表7可以作为野外地形图测量高程注记点精度指标。

5 结论

根据以上分析，对于1:500或1:1000地形图测量，在用于土石方工程量计算时，测点高程精度将直接影响其工程量计算，综合考虑表7和工作实际，建议要求测点对于测

[1]GB 50026－2007，工程测量规范[S]．

[2]DL/T 5001－2004，火力发电厂工程测量技术规程[S]．

[3]SL 197－97，水利水电工程测量规范[S]．

[4]DL/T 5173－2012，水电水利工程施工测量规范[S]．

[5]杨成贵，罗奎，郑潇潇．土石方工程的误差分析[J]．天然气与石油，2010，28(6)．

[6]李志林，朱庆．数字高程模型[M]．武汉：武汉大学出版社，2000．

[7]高井祥. 测量学[M]. 徐州：中国矿业大学出版社，2002.

Effect of Relief Map Measure Precision on Calculation of Earth Stone Square

HU Ji-lun, CHENG Zheng-feng, XYU Hui
(China Southern Electric Power Design Institute, Wuhan 430071, China)

In order to meet the design requirement on earthwork quantity calculation，this article analyses the similarities and differences on topographic map survey in the different surveying specifications, analysis the total station triangle elevation measurement accuracy and propose topographic point elevation accuracy index and topographic point note spacing requirements. At the same time, this article analyses the influence on earthwork calculation from point elevation accuracy.

spacing of the elevation ooint; elevation difference accuracy; earthwork quantity

P2

B

1671-9913(2014)03-0027-06

10.13500/j.cnki.11-4908/tk.2014.03.006

2013-05-27

胡吉伦(1957- )，男，湖北鄂州人，高级工程师，目前从事电力工程测量工作。