拱型波纹屋盖脉动风作用下应力风振系数研究
张德生,李远瑛
(嘉应学院 土木工程学院,广东 梅州 514015)
拱型波纹钢屋盖结构具有很多优点[1],已经在工程中得到了应用.但是由于结构跨度大、自重轻,在风荷载作用下容易因为吸力发生向上拱起变形,造成屋盖掀开破坏.结构在脉动风作用下也会引起结构振动,因此有必要研究结构在脉动风作用下的动力响应.
本文以W666型金属拱形波纹屋盖为研究对象,跨度为18 m、30 m,支座约束形式为固支和铰支,在不同矢跨比(0.15、0.25、0.3)条件下,利用ANSYS有限元分析软件研究结构在脉动风作用下的内力响应及内力风振系数,为该结构设计、施工及同类型大跨轻型屋盖的风致振动提供参考和借鉴.
1 风荷载计算
在随机风场作用下,大跨度结构上的风压为:
w=μsμzwo+μswp,
(1)

考虑空间各点的相关性,18 m跨度波纹拱沿拱轴线等距离选取为13点,30 m跨度波纹拱为21点.波纹拱矢跨比为0.25时各点位置见图1(a)(b).
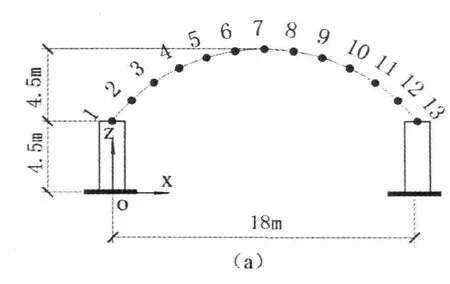
图1 18 m 跨波纹拱模拟各点位置图
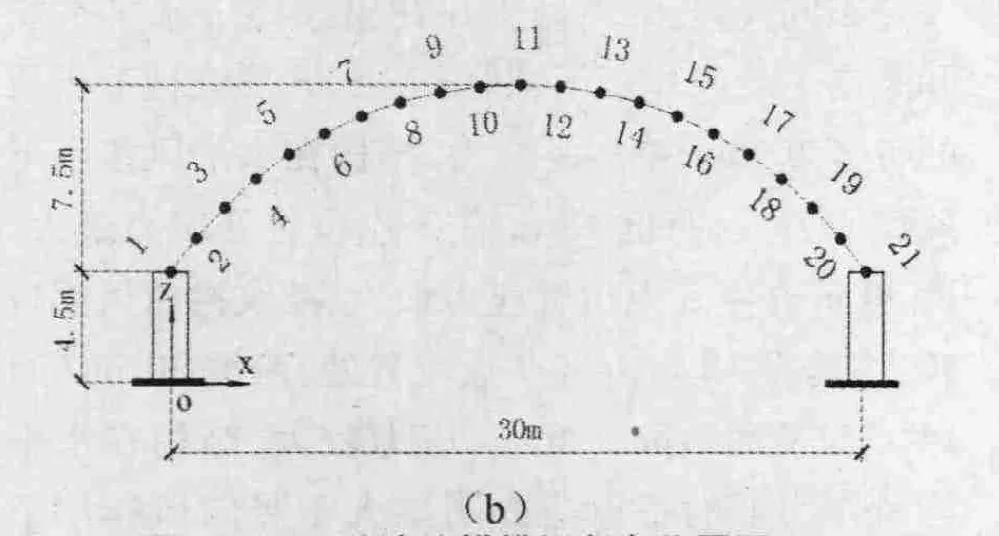
图1 30 m 跨波纹拱模拟各点位置图
2 风振响应分析
2.1 有限元模型的建立
文中以W666型金属拱形波纹屋盖为研究对象,跨度为18 m、30 m,支座约束形式为固支和铰支,矢跨比为0.15、0.25、0.3.波纹拱计算模型采用文献[3],各弹性常数采用文献[4]的实验数据.有限元模型采用文献[5].图2为跨度30 m( 矢跨比为0.25) 、板厚为1.2 mm、支座为固支的W666拱型波纹屋盖计算单元有限元模型.

图2 波纹供计算单元有限元模型
2.2 Von-Mises等效应力[6]
波纹拱上各点处于复杂的三维空间应力状态.在整体坐标下,利用六个等效应力分量可根据式(2)计算Von Mises等效应力:
(2)
根据 Von Mises 屈服准则:材料在复杂应力状态下的形状改变能达到了单向拉伸屈服时的形状改变能,即只要满足式(3)则材料开始屈服.
(3)
其中,σT是材料单向拉伸时的屈服极限.
2.3 波纹拱风振响应
将波纹拱各节点处风速时程按照公式(1)转化为风荷载时程,将各时间步风荷载加载到波纹拱各单元上,利用瞬态分析中的完全法(Full)对结构各工况进行脉动风荷载时程分析,计算分为1 000个荷载步,每步0.1 s,共100 s,得到结构各节点应力响应.图3(a)~3(d)出各节点在水平平均风和脉动风作用下的Von Mises应力及应力均方根值.图4(a)~4(d)给出各节点在竖向平均风和脉动风作用下的Von Mises应力及应力均方根值.

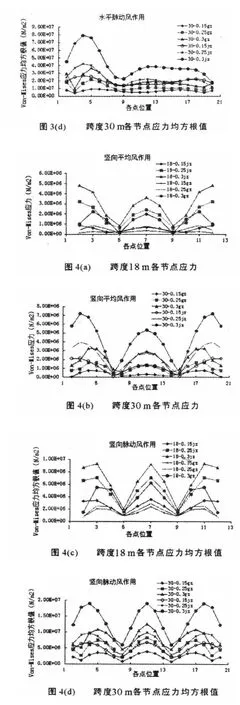
不同矢跨比、不同支座约束条件下水平平均风和竖向平均风作用下,利用ANSYS非线性分析得到的各节点Von-Mises应力.结构在水平风作用下迎风面应力大,跨度18 m在3点位置处应力最大,跨度30 m在4、5点位置应力最大.波纹拱背风面应力较大,跨度18 m在8、9点位置处,跨度30 m在13、14点位置处Von-Mises应力较大.结构在水平平均风作用下的各点应力明显大于竖向风作用下的应力.结构在竖向平均风作用下,两端部节点及跨中节点应力较大.结构各点应力随着跨度、矢跨比的增加而增大;结构为固支波纹拱的各点应力小于铰支波纹拱.
图3(c)、3(d)、4(c)、4(d)为波纹拱在水平脉动风和竖向脉动风作用下利用ANSYS瞬态时程分析得到的各节点Von-Mises应力响应均方根值.结果表明,结构在脉动风作用下各点应力变化特点与平均风作用相一致.结构在脉动风作用下的各节点应力均方根值大于在平均风作用下的应力,且水平脉动风作用下的各节点应力均方根值大于在竖向脉动风作用下的应力.
2.4 波纹拱应力风振系数
风振系数通常定义为风引起的结构总响应与平均风引起的响应之比[7].动荷载可以转化为静荷载和动力效应系数的乘积,动力效应系数可以由位移风振系数和内力风振系数表示.本文研究内力风振系数对结构风致振动的影响,内力风振系数采用的计算公式为:
式中σsi为平均风产生的各节点应力,σDi为脉动风产生的各节点应力响应,风荷载作用下结构的应力总响应为σzi.
表1给出节点在水平脉动风作用下的应力风振系数.由图4(a)~4(d)可以得到矢跨比为0.15波纹拱在水平平均风作用下的各节点应力很小,在脉动风作用下各节点的应力相对水平平均风作用较大,因此有些节点内力风振系数较其他工况波纹拱偏大.矢跨比为0.25、0.3波纹拱各节点应力风振系数较为接近.因波纹拱在竖向平均风作用下各节点应力小,而竖向脉动风作用相对竖向平均风较大,因此各节点在竖向脉动风作用下应力风振系数较大,但其应力风振系数在总风荷载作用下不起控制作用,本文不再列出其计算结果.

3 结论
(1)由图3(a)、3(b)、4(a)、4(b)可以得到,结构在水平风作用下迎风面处Von-Mises应力最大,在背风面处Von-Mises应力较大.结构在水平平均风作用下的各点应力明显大于在竖向风作用下的应力.结构在竖向平均风作用下,两端部节点及跨中节点应力较大.结构各点应力随着跨度、矢跨比的增加而增大;结构为固支波纹拱的各点应力小于铰支波纹拱.
(2)由图3(c)、3(d)、4(c)、4(d)可以得到,波纹拱在水平脉动风和竖向脉动风作用下各点应力变化特点与平均风作用相一致.结构在脉动风作用下的各节点应力均方根值大于在平均风作用下的应力,且水平脉动风作用下的各节点应力均方根值大于在竖向脉动风作用下的应力.
(3)矢跨比为0.15波纹拱在平均风作用下的各节点应力相对较小,在脉动风作用下各节点的应力相对较大,因此矢跨比为0.15波纹拱各节点应力受脉动风影响相对较大.矢跨比为0.25、0.3波纹拱内力风振系数较为接近.
(4)通过对不同工况条件下最大应力位置处应力风振系数比较可以得出,在其他相同条件下,应力风振系数随着结构的跨度增大而增大,随着矢跨比的增加而减少.在其他条件相同时,支座约束为固支波纹拱的风振系数小于铰支波纹拱.对于大跨度轻型钢屋盖要考虑脉动风对结构内力的影响.因此在设计、施工过程中优先选择支座约束强、矢跨比相对较小的波纹拱.
[1] 刘锡良.一种新型空间钢结构——银河金属拱型波纹屋顶[J].建筑结构学报,1996,17(4):72-75.
[2] 张相庭.工程抗风设计计算手册[M].北京:中国建筑工业出版社,1998:176.
[3] 王小平,蒋沧如,胡春宇,等.18M跨W666金属拱型波纹屋顶试验中的测试技术[J].测试技术学报,1998,12(3):283-287.
[4] 王小平, 蒋沧如,李桂青. 金属拱型波纹屋面计算模型的简化[J]. 钢结构,1999(4):8-10.
[5] 李远瑛,张德生.拱型波纹屋盖结构在风荷载作用下可靠度数值模拟[J].空间结构,2013,19(2):51-56.
[6] 殷绥城.弹塑性力学[M].北京:中国地质大学出版社,1990:31-32.
[6] 周颖.双层网壳屋盖的风振响应和风振系数研究[D].天津:天津大学,2004:32-34.

