Banach空间中Ishikawa迭代收敛定理

顾朝晖

(广东外语外贸大学 思科信息学院， 广州 510006)

0引言及预备知识

许多学者对平均非扩张映射的不动点问题做了很多研究，其中张石生[1]、赵汉宾[2]、杨姗姗[3]分别证明了平均非扩张映射在Banach空间中的不动点的存在性.自从Ishikawa[4]提出Ishikawa迭代以来，学者对Ishikawa迭代法收敛性做了许多研究，文献[5]～[11]分别在不同空间得到了不同映射的Ishikawa迭代的收敛性定理，其中文献[10]在研究一致Lipschitz 渐近伪压缩映象和非扩张映象不动点的迭代逼近时, 给出了迭代序列强收敛的充要条件，文献[11]给出了φ强增生型变分包含的Ishikawa迭代序列强收敛的充要条件.本文主要研究平均非扩张映射的Ishikawa迭代收敛的充要条件.

定义1设X是Banach空间，T是X到X的映射，若∀x，y∈X,a,b≥0,a+b≤1，

‖Tx-Ty‖≤a‖x-y‖+b‖x-Ty‖，

(1)

则称T为平均非扩张映射.

定义2[4]设X是Banach空间，T为平均非扩张映射.若序列{xn}满足

yn=βnTxn+(1-βn)xn，

(2)

xn+1=(1-αn)xn+αnTyn，

(3)

则称序列{xn}是关于{αn}，{βn}⊆[0，1]的Ishikawa迭代.

1 主要结论及其证明

在证明平均非扩张映射的Ishikawa迭代收敛的充要条件前，给出相关引理.

引理设X是Banach空间，T:D(T)→X是具有不动点的平均非扩张映射，则对∀x0∈X，T的Ishikawa迭代序列有界.

证明设F(T)是T的不动点集，p∈F(T)，则

‖Tx-p‖=‖Tx-Tp‖≤a‖x-p‖+b‖x-Tp‖≤ (a+b)‖x-p‖ ≤‖x-p‖.所以

‖xn+1-p‖ =‖ (1-αn)xn+αnTyn-p‖ = ‖(1-αn)(xn-p)+αn(Tyn-p)‖≤(1-αn)‖xn-p‖+αn‖Tyn-p‖≤ (1-αn)‖xn-p‖+αn‖yn-p‖= (1-αn)‖xn-p‖+αn‖βnTxn+(1-βn)xn-p‖=(1-αn)‖xn-p‖+αn‖βn(Txn-p)+(1-βn)(xn-p‖)≤(1-αn)‖xn-p‖+αnβn‖Txn-p‖+αn(1-βn)‖xn-p‖≤ (1-αn)‖xn-p‖+αnβn‖xn-p‖+αn(1-βn)‖xn-p‖ =‖xn-p‖≤…≤‖xn-1-p‖ ≤…≤‖x0-p‖，.所以{xn}为有界序列.

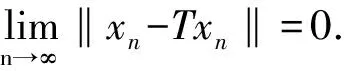
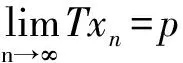
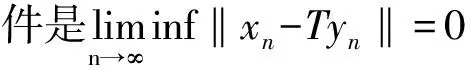
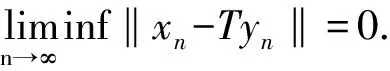
从定理2的证明中可以得到下面几个推论：

[1] 张石生. 关于Banach空间中平均非扩张映射的不动点理论[J].四川大学学报，1975(2):67-78.

[2] 赵汉宾.Banach空间中的平均非扩张映射不动点的存在理论[J]. 数学学报，1979，22(4): 459-469.

[3] 杨姗姗.Banach空间中平均非扩张映射的不动点问题[J]. 哈尔滨工业大学学报，2003，35(6):660-662.

[4] S. ISHIKAWA.Fixed points by a new iterations method[J]. Proc. Amer. Math. Soc. 1974(44): 147-150.

[5] 邓磊,李胜宏. 一致凸Banach空间中非扩张映射的I shikawa迭代[J]. 数学年刊,2000, 21A(2) : 159-164.

[6] XU H K. Strong convergence of an iterative method for nonexpansive and accretive opertors[J]. J Math Anal Appl, 2006(314):631-643.

[7] SU Y F， ZHANG F， QIN X L. Strong Convergence Theorems for Nonexpansive Mapping in Banach Spaces. Acta Analysis Functionalis Applicata[J]. 2007, 9(3): 212-219.

[8] GUZ H , LI Y J . Approximating Fixed Points of Mean Nonexpansive Mapping in Banach Spaces[J]. Int.J.Pure Appl.Math, 2007，40(2)： 201-208.

[9] GUZ H , LI Y J Approximation Methods for Common Fixed Points of Mean Nonexpansive Mapping in Banach Spaces[J]. Fixed Point Theory and Applications, Volume 2008 (2008), Article ID 471532, 7 pages.

[10] 王朝, 刘理蔚. 渐近伪压缩映象的Ishikawa迭代序列强收敛的充要条件[J]. 应用泛函分析学报, 2006, 8( 2) :252-258.

[11] 薛祖华, 顾正刚. φ-强增生型变分包含的Ishikawa迭代序列强收敛的充要条件[J]. 应用泛函分析学报, 2010, 12(1) :91-96.