带有多元算子李代数的线性基底
黄炬委
(嘉应学院 梅州师范分院,广东 梅州 514072)
0 引 言


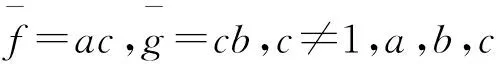
Shirshov的引理被称为李代数和结合代数的合成钻石引理(Composition-Diamond lemma for Lie and associative algebras).
另外,这种方法同时被H. Hironaka在研究幂序列代数和B. Buchberger[11,12], 在研究多项式代数中发现.B.Buchberger命名其为“Gröebner”基.Gröebner基理论在数学(尤其是代数几何),计算机科学和信息学等中有着相当重要和广泛的应用.
现今,在许多不同的代数系统中(结合或非结合)都有相应的合成钻石引理.在证明代数系统的合成钻石引理时首先要找到这个代数的自由对象.
令K是有单位的交换环,K〈X;Ω〉 是K上的一个带多元算子的自由结合代数,Lie(X;Ω) 是带多元算子的自由李代数.在这本文中我们利用自由李代数的合成钻石引理找到Lie(X;Ω)的一个线性基底,并由此建立了Lie(X;Ω)的自由对象.
1 预备知识
设k是一个域,Lie(X)是k上的由X生成的自由李代数,X*是由X生成的自由幺半群. 对每个u=xi1xi2...xim∈X*,记|u|x为u的长度,即|u|x=m. 幺半群X*上良序 >是一个项序, 如果它跟字的乘法是相容的,即对任意的u,v∈X*,有 (∀w1,w2∈X*)uv⟹w1uw2w1vw2.
在X*一个典型的项序就是次数字典序,即先比较两个字的长度,再按照字典序来比较.我们使用X*上的两个线性序:
(i)(字典序)t<1,如果t≠1, 用归纳法;如果u=xiu',v=xjv',那么u 把Lie(X)看成是自由结合代数k〈X〉的自由子李代数,它是在李括积[u,v]=uv-vu下由X生成的. 定义1.1[7]w∈X*{1} 是一个结合的Lyndon-Shirshov字(简写为 ALSW),如果 (∀u,v∈X*,u,v≠1)w=uv⟹vu 把X上所有的ALSW记成集合ALSW(X), (1) 如果w=uv∈ALSW(X),这里u,v≠1,则v w=c1c2…cn,这里c1…,cn∈ALSW(X),且c1≤c2≤…≤cn;(4) 如果u''=u1u2,u''=u2u3∈ALSW(X),则u=u1u2u3∈ALSW(X);(5) 如果w∈ALSW(X),w=uv,v是最长的真子字,且v∈ALSW(X), 则u∈ALSW(X) 定义1.2[ 7]X中的一个非结合字(u)称为非结合的Lyndon-Shirshov字(简写为NLSW ),记为[u],如果 (i)u∈ALSW(X); (ii)如果[u]=[(u1)(u2)] ,则 (u1)和(u2)都是NLSW(由 ALSW的定义知u1>u2); (iii)如果[u]=[[[u11][u12]][u2]] ,则u12 把 X上所有的NLSW记成集合NLSW(X), 从文献[7,13 ]得知,对任意w∈ALSW(X),存在唯一的打括号方式使得 [w]∈NLSW(X):[w]=w,如果w∈X,且[w]=[[u][v]],如果|w|x>1,这里的v是w的最长的真子字,且v是结合的Lyndon-Shirshov字,由(5)知u∈ALSW(X).再对|w| 作归纳,可以得到[w]. 引理1.4[14]假定w=aubvc,其中w,u,v∈ALSW(X)则w有下面的打括号. [w]u,v=[a[u]b[v]d]. Ωn={ω1(n)<ω2(n)<…是n元(ary)运算,比如,n-ary(ω)=n,如果ω ∈Ωn. 在Ω上定义一个序,Ω1<Ω2<…<Ωn<…定义 〈X;Ω〉0=S(X0),X0=X, 〈X;Ω〉1=S(X1),X1=X∪Ω(〈X;Ω〉0). 定义 〈X;Ω〉n=S(Xn),Xn=X∪Ω(〈X;Ω〉n-1),n>1 得到 〈X;Ω〉0⊂〈X;Ω〉1⊂…⊂〈X;Ω〉n⊂…, 下面给出几个记号: 〈X;Ω〉表示X上带有多元线性算子Ω的所有结合字; (X;Ω)表示X上带有多元线性算子Ω的所有非结合字; X*表示上的所有结合字; X**表示上的所有非结合字. 对于任意u∈〈X;Ω〉,dep(u)=min{n|u∈〈X;Ω〉n}称为u的深度.K〈X;Ω〉是由〈X;Ω〉张成的K-代数.〈X;Ω〉 (相对于K〈X;Ω〉)中的元素称为Ω-字(称Ω-多项式).如果u∈X∪Ω(〈X;Ω〉)称u是一个素Ω-字,且定义|u|=1(u的长度为1).如果u=u1u2…un∈ 〈X;Ω〉,ui是一个素Ω-字,对任意的i,定义|u|=n. 对于每一个ω∈Ωn,定义ω:〈X;Ω〉n→〈X;Ω〉,(x1,x2…,xn)|→ ω(x1,x2,…,xn).通过这种方式把 〈X;Ω〉线性张成K〈X;Ω〉.易知K〈X;Ω〉是一个由集合X生成的在K上带有多元线性算子Ω的自由结合代数. 首先,在素Ω-字定义一个序:ut,vt∈X∪Ω(〈X;Ω〉),ut>vt当且仅当下面其中一个条件成立: (a)ut,vt∈X且ut>vt; (b)ut=ωi(uk1,…,ukt),vt∈X; (c)ut=ωi(uk1,…,ukt),vt∈ωj(vk1,…,vks),且ωi>ωj,或者ωi=ωj且(uk1,…,ukt)>(vk1,…,vks)(字典序比较). 再次,在Ω-上定义一个序:对于任意u∈〈X;Ω〉有u=u1u2…un.ui∈X∪Ω(〈X;Ω〉).令wt(u)=(u1,u2,…un),v=v1v2…vm.定义u>v⟺wt(u)>wt(v) 字典序, 用degx(u)记u中x∈X的个数;用 |u|记ui∈X∪Ω(〈X;Ω〉)的个数(u的长度).比如,如果u=ω1(x1,x2)x3x4ω2(x5)∈〈X;Ω〉,则有degx(u)=5 且 |u|=4. 最后,使用 〈X;Ω〉上的两个线性序: (字典序)u>v⟺wt(u)>wt(v) (1) (次数字典序)u>v⟺degx(u)>degx(v)或者(degx(u)=degx(v),wt(u)>wt(v)) (2) 定义2.1, 令u∈〈X;Ω〉,<为(1)中定义在〈X;Ω〉上的序.我们称u是一个ALSW, 如果下面条件之一成立: i)u∈X是一个ALSW;ii) 如果(任意v,w∈〈X;Ω〉)u=vw⟹vw>wv,这时u是ALSW;iii) 如果ui是ALSW,这时u=ω(n)(u1,u2,…,un)是ALSW. 对于u∈ALSW,u=u1u2…un,ui∈X∪Ω(〈X;Ω〉),我们对dep(u) 作归纳法来介绍两种打括号方式: (1)如果dep(u)=0 ,ui∈X,有如下两种打括号方式[16]. 一种是由上到下打括号,由下面的归纳定义给出 [xi]=xi,[u]=[[v][w]], 例1 于dep(u)=0,u∈X*,令u=x2x2x1x1x2x1有 [u]→[[x2x2x1x1][x2x1]]→[[x2[x2x1x1]][x2x1]]→[[x2[[x2x1]x1]][x2x1]] 另一种是由下到上打括号.用同样的例子来解释u=x2x2x1x1x2x1.把最小的字x1和前面一个字粘在一起:u|→x2[x2x1]x1[x2x1],非结合字x2[x2x1]和x1构成了一些新的字母,用字典序来定义它们,就是说,x2[x2x1]>x1.把最小的字x1和全面一个字粘在一起:x2[x2x1]x1[x2x1] |→x2[[x2x1]x1][x2x1],构成了一些新的字母x2>[x2x1]>[[x2x1]x1].把最小的字[[x2x1]x1] 和前面一个字粘在一起:x2[[x2x1]x1][x2x1]|→[x2[[x2x1]x1]][x2x1]构成了一些新的字母 [x2[[x2x1]x1]]>[x2x1].把最小的字[x2x1]和前面的一个字粘在一起: [x2[[x2x1]x1]][x2x1]|→[[x2[[x2x1]x1]][x2x1]]=[u]. (2)如果dep(u)=m>0,假定任意v∈〈X;Ω〉,dep(v) 对于u=u1u2…un,其中ui∈X∪Ω(〈X;Ω〉)且对于每一个ui利用dep(u)上归纳法打括号,方式如下: i)对于ui∈X,由于dep(ui)=0,有[ui]=ui; ii)对于ui∈Ω(〈X;Ω〉),有ui= ωki(n)(ui1,ui2…uim)且dep(uij) 如上所述,可以如下两种方法对u打括号: 一种是对|u| 归纳定义的由上到下打括号: 例2 对于dep(u)=1,令u=ω2(x3x2x1,x2x1)x2x1ω1(x2x2x1)x1,采用由上到下的打括号,得到u→ω2([x3[x2x1]],[x2x1])x2x1ω1([x2[x2x1]])x1→[ω2]([x3[x2x1]][x2x1])x2x1ω1([x2[x2x1]])x1]]→[[ω2([x3[x2x1]][x2x1])[x2x1]]ω1([x2[x2x1]])x1]]. 另一种是由下到上打括号,用相同的例子解释 u→ω2([x3[x2x1][x2x1])x2x1ω1([x2[x2x1])x1→ω2([x3[x2x1]],[x2x1])2x1ω1([x2[x2x1]])x1→ω2([x3[x2x1]][x2x1])x2x1ω1([x2[x2x1]])x1→[ω2([x3[x2x1]],[x2x1])[x2x1]][ω1([x2[x2x1]])x1→[[ω2([x3[x2x1]],[x2x1])[x2x1]][ω1([x2[x2x1]])x1]]. 注:我们用 []来表示由下到上的打括号,用 [[]]来表示由上到下的打括号. 对于ui∈Ω(〈X;Ω〉) ,有ui=ωki(n)(ui1,ui2,…,uin)且dep(uij) 在这基础上再对 |u|作归纳法证明,证明方式可参考[16]. 定义2.3令<为(1)中定义在 〈X;Ω〉且 (u)是一个非结合字. (u)称为非结合的Lyndon-Shirshov字(简写为 NLSW),记为 [u],如果 由归纳可知,([v1][w])=∑γi([ti],ti>min{v1,w}=w; ([v2][w])= ∑γj'[tj',tj'min{v2,w}=w,这时u=∑γi([ti][v2])+∑γj'([v1][tj'])且有min{ti,v2},min{tj',v1} 情形2 对于 (u)∈(X;Ω),如果 (u)=ω(n)(u1,u2,…,un),对dep(u)做归纳证明. 如果dep(u)=1 ,有 (u)=ω(n)(u1,u2,…,un),且对任意ui,有dep(ui)=0 .由归纳可知,(ui)=∑αiji[uiji],(u)=ω(n)(∑α1j1[u1j1],∑α2j2[u2j2]…∑αnjn[unjn]) =∑γα1j1α2j2…αnjnω(n)([u1j1][u2j2],…,[unjn]) 现在可以对dep(u)作归纳证明得到结论. 情形3 如果(u)中的子字包含情形1和情形2,那么可以类似于情形1的方式来证明. 引理2.7所有的NLSW是k-无关的. 由引理2.5和引理 2.7,得到 推论2.8所有的NLSW构成了Lie(X;Ω)的线性基底. 由推论2.8和引理2.6有 定理2.10Lie(X;Ω) 是在集合X上带有多元线性算子Ω 的自由李代数. [1] SHIRSHOV A I . Some algorithmic problem for Lie algebras[M]. Sibirsk. Mat. Z., 3, 292-296(1962) ; English translation in SIGSAM Bull., 33(2):3-6(1999). [2] MAGNUS W. über diskontinuierliche Gruppen miteiner definierenden Relation (Der Freiheitssatz)[J]. J. Reine Angew. Math., 163: 141-165(1930). [3] MAGNUS W . Das Identitä ts problem für Gruppen mit einer definierenden Relation[J]. Math. Ann., 106: 295-307(1932). [4] MAGNUS W.KARRASS,A SOLITAR D Combinatorial. group theory[J] Dover Publications, Inc. New Youk, 1976. [5] LYNDON R C, SCHUPP PE .Combinatorial Group Theory[J]. Springer-Verlag, 1977. [6] SHIRSHOV A I. Some algorithmic problem for Lie algebras[J].Sibirsk. Mat. Z., 3, 292-296(1962); English translation in SIGSAM Bull., 33(2).3-6(1999). [7] SHIRSHOV A I. On free Lie rings[J]. Mat. Sb., 45(87),113-122(1958). [8] SHIRSHOV A I. Some algorithmic problem for Lie algebras[J]. Sibirsk. Mat. Z., 3, 292-296(1962) ; English translation in SIGSAM Bull.,1999 33(2): 3-6. [9] BOKUT LA. Imbeddings into simple associative algebras[J]. Algebra i Logika, 1976 15:117-142. [10] BERGMAN G M. The diamond lemma for ring theory[J]. Adv. In Math., 29, 178-218(1978). [11] BUCHBERGER B. An algorithm for finding a basis for the residue class ring of a zero-dimensional polynomial ideal [J]. Ph.D. thesis, University of Innsbruck, Austria, (1965). [12] BUHBERGER B. An algorithmical criteria for the solvability of algebraic systems of equations[J].Aequationes Math., 4, 374-383(1970). [13] LYNDON RC. On Burnside's problem I[J]. Trans. Amer. Math.Soc., 1954(77):202-215. [14] BOKUT LA. GP KUKIN. Algorithmic and Combinatorial Algebra[J]. Kluwer Academic Publishers, (1994). [15] BOKUT LA CHEN Yuqun , QIU Jianjun .Gröobner-Shirshov bases for Associative Algebras with Multiple Operators and Free Rota-Baxter Algebras, arXiv: 0805.0640v2. [16] BOKUT LA, CHEN YuQun. Gröbner-Shirshov bases for Lie algebras: after A.I. Shirshov[J]. Southeast Asian Bull. Math., 2007 31, 1057-1076.

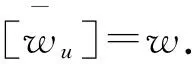
2 带有多元算子李代数的线性基底


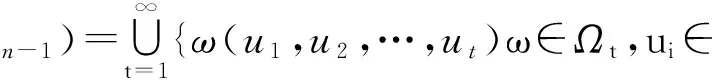
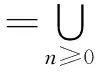
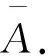

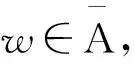

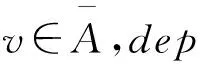
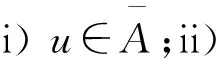





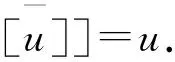



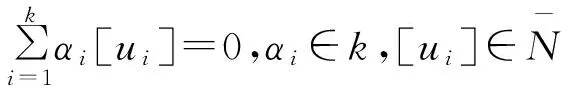

3 带有多元算子的自由李代数