推广的积分第一中值定理的应用*

庄科俊

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

引言

定积分是数学分析的重要组成部分，而积分中值定理则是定积分的重要性质之一. 积分中值定理揭示了一种将积分化为函数值，或者将复杂函数的积分化为简单函数的积分的方法，在求极限、判定某些性质点、估计积分值等方面有着重要而广泛的应用. 因此，加强学生对积分中值定理，特别是基本的积分第一中值定理的应用能力，就显得尤为重要了.

在现行的数学分析教材[1，2]中，积分第一中值定理关于介值点ξ的范围，在课后习题中都加强到了开区间内，证明可见文献[3]. 定理内容叙述如下.

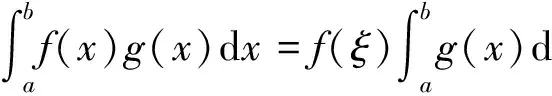
目前，已有不少文献对积分第一中值定理进行了推广和改进，并且给出了详细的证明，如文献[4～6]. 然而，关于推广的积分第一中值定理的应用却很少[7]. 因此，本文将通过具体的例题，来展示推广的积分第一中值定理在求解某些积分问题中的优越性.

1 推广的积分第一中值定理的应用

1.1 在积分极限计算中的应用

对积分号下取极限的问题，通常可以运用定积分的基本性质，特别是推广的积分第一中值定理，把积分化为简单易求的表达式.

证明1)由推广的积分第一中值定理，存在ξ∈(0,1)，使得：

2)由推广的积分第一中值定理，存在ξ∈(0,1)，使得：

1.2 在定积分不等式中的应用

在证明定积分不等式时，往往可以考虑运用积分中值定理，以便可以去掉积分符号. 如果被积函数是两个因子的乘积，还可以借助推广的积分第一中值定理，使积分便于计算.

分析 这是定积分不等式的证明，由于两个定积分的积分限相同，故可以合并成一个定积分. 为了方便计算，可以考虑将被积函数的一个因子提到积分号的前面.

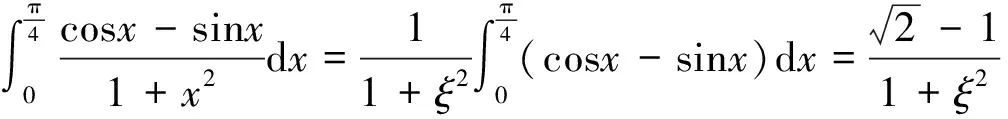
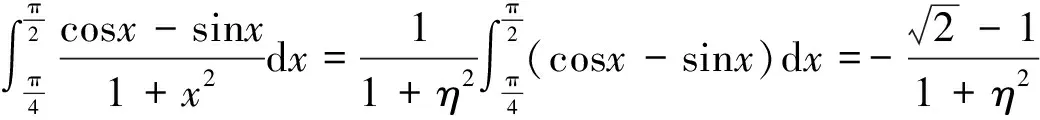
所以：

1.3 在积分等式证明中的应用

对于一些较为复杂的定积分的极限证明问题，还需要综合其它方法，如分部积分法、定积分的区间可加性、迫敛性等，对问题加以简化.

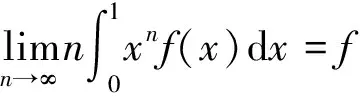
证明因为 ：

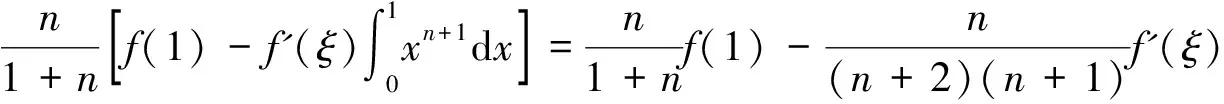
由f'(x)在[0,1]上的连续性，可知其有界. 对上述等式两边取极限，令n→∞，可得结论.

例4 (中国科学院2003年考研题)设f(x)在[-1,1]上连续，证明：

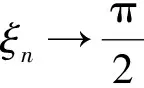
分析 直接对定积分进行计算是不容易的，因此可以考虑用推广的第一积分中值定理将f(x)提到积分号的外面. 但是，在h=0的充分小的右邻域内，点x=0是被积函数的瑕点. 因此，在使用推广的积分第一中值定理时，需要对定积分的区间进行拆分.

为简便起见，将上述表达式记为I1+I2+I3.

由于f(x)在[-1,1]上连续，所以f(x)有界，设|f(x)|≤M. 于是有：

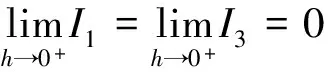
证明对任意的ε∈(0,1)，有：

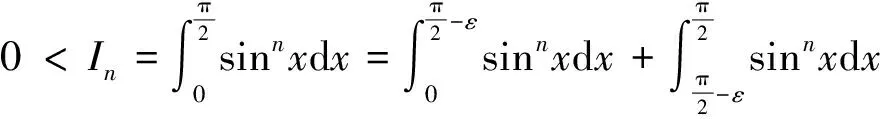
2 结束语

本文通过典型的例题，对推广的积分第一中值定理的应用作了具体的说明. 实际上，定积分的这一重要性质也可应用于很多其他问题，这需要在教学实践中不断地探索.

参考文献：

[1]华东师范大学数学系. 数学分析(上册)[M]. 第4版.北京：高等教育出版社，2010.

[2]刘玉琏. 数学分析讲义(上册)[M]. 第5版. 北京：高等教育出版社，2008.

[3]谢惠民，恽自求，易法槐，等. 数学分析习题课讲义(上册)[M]. 北京：高等教育出版社，2003.

[4]李仕琼，梁波. 积分第一中值定理的证明及其推广[J]. 重庆文理学院学报，2006,5(3)：14-16.

[5]李衍禧. 积分第一中值定理的推广[J]. 数学的实践与认识，2007,37(9)：203-206.

[6]文传军，姚俊. 推广的积分第一中值定理的再改进[J]. 高等数学研究，2011,14(1)：42-44.

[7]张国铭. 改进的积分第一中值定理的应用[J]. 高等数学研究，2011,14(6)：25-27.