向量夹角余弦的IOWHA算子的变权系数区间型组合预测模型*
袁宏俊,胡凌云,徐 凤
(1. 安徽财经大学统计与应用数学学院,安徽 蚌埠 233030; 2. 安徽财经大学管理科学与工程学院,安徽 蚌埠 233030)
引言
1969年Bates J.M.和Granger C.W.J.为了提高预测精度,首次采用将不同预测方法组合而成研究预测问题[1].随后国内外的学者不断的深化和改进,提出许多较精确的实数型组合预测方法[2~6].由于在客观世界中人们往往会遇到预测信息的不确定性和模糊性,在已有实数型组合预测方法的基础上,有必要开展区间型组合预测方法的研究.文献[7]对区间时间序列分析中,采用MSEI和MRIE两种预测效率分析,对比研究区间时间序列预测准确度.文献[8,9]分别从最大误差绝对值达到最小的误差指标、向量夹角余弦的相关性指标方面开展定权系数区间型组合预测方法研究.文献[10~12]都从有序信息集结算子方面开展变权系数区间型组合预测方法研究.在上述文献的基础上,本文对模糊信息是区间数的预测问题中,将区间数的左、右端点作为研究的切入点,考虑到左、右端点都会在不同时刻的预测精度有高有低的现象,采用变权系数组合预测方法的思想,引入IOWHA的信息集结算子,以向量夹角余弦为准则,将实际值和组合预测值的区间数左、右端点时间序列分别建立变权系数多目标最优组合预测模型,通过特定方法将其转化成单目标最优组合预测模型借助Lingo实现求解,最后实例分析采用文献[7]中数据,运用文中构建的单目标组合预测模型加以计算,误差指标结果显示优越于各单项预测方法.
1 基本概念

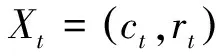
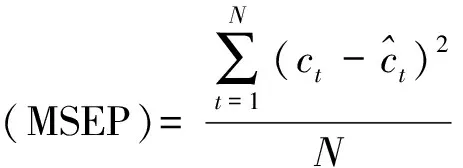
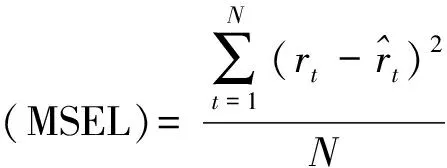
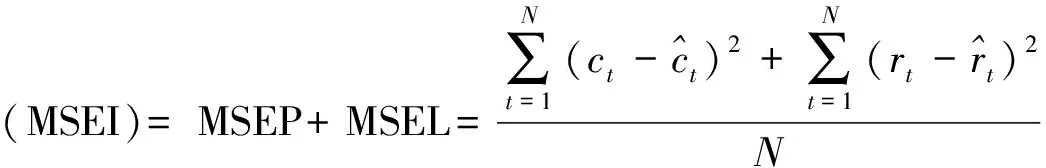
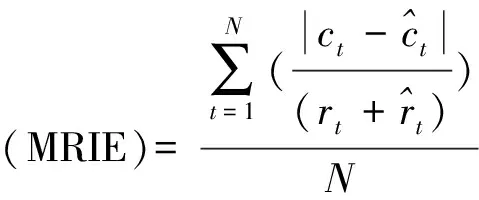
定义3[4]设f:R+n→R+是n元函数,定义:

定义4[4]设(v1,a1),(v2,a2),…,(vn,an)为n个二维数组,定义:


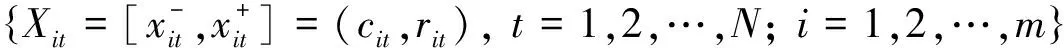
定义5[12]记:
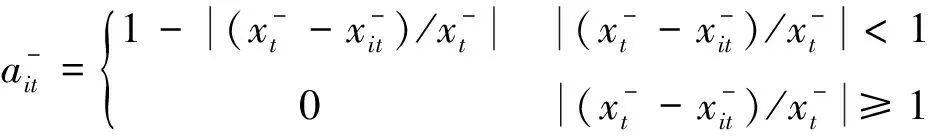

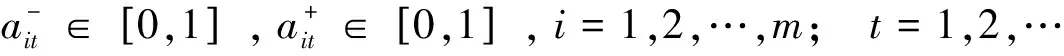
定义6 记:

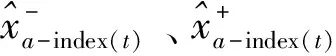
上述定义中IOWHA算子组合预测值区间数左、右端点公式改写成倒数形式表示为:
定义7 记:
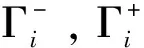
称Γ-,Γ+分别为IOWHA算子的组合预测值区间数和实际值区间数的两端点倒数序列的向量夹角余弦.
2 构建向量夹角余弦的IOWHA算子的变权系数区间型组合预测模型
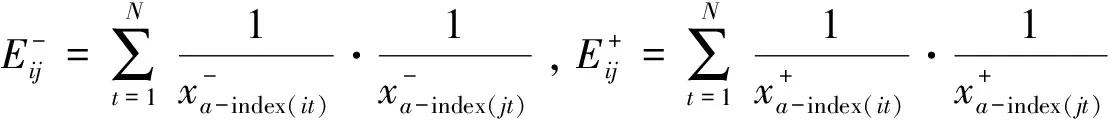
这样,定义7可化简成:
显然,上述公式中向量夹角余弦Γ-、Γ+都是含有L=(l1,l2,…,lm)T的函数,可以表示为Γ-(L)和Γ+(L),而向量夹角余弦值是夹角越小数值越大,表明两序列越接近,所以为了更好地刻画组合预测值区间数和实际值区间数的拟合程度,用实际值区间数的两端点和IOWHA算子的组合预测值区间数的两端点的倒数向量夹角余弦值来描述,设R=(1,1,…1)T,则构建如下区间数左、右端点处的变权系数多目标最优组合预测模型:
(1)
为了更方便地求解模型(1),引入偏好系数k(0≤k≤1)到模型(1)中,则可其转化为简单的单目标最优组合预测模型:
(2)
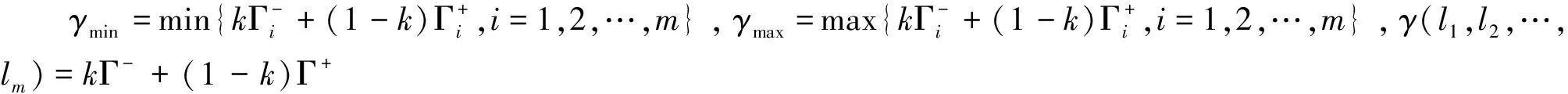
3 实例分析
为了检验本文提出的变权系数区间型组合预测方法是否合理有效,现应用文献[7]中的数据进行实例分析,具体原始数据见表1.
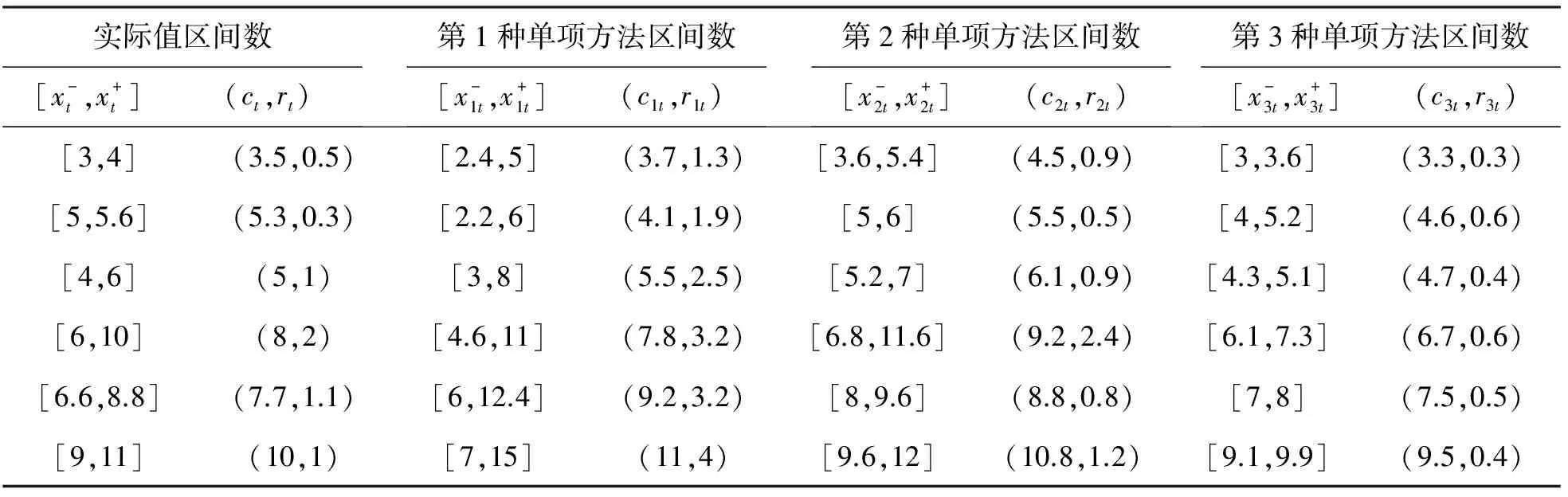
表1 各类区间数及等价形式的原始数据
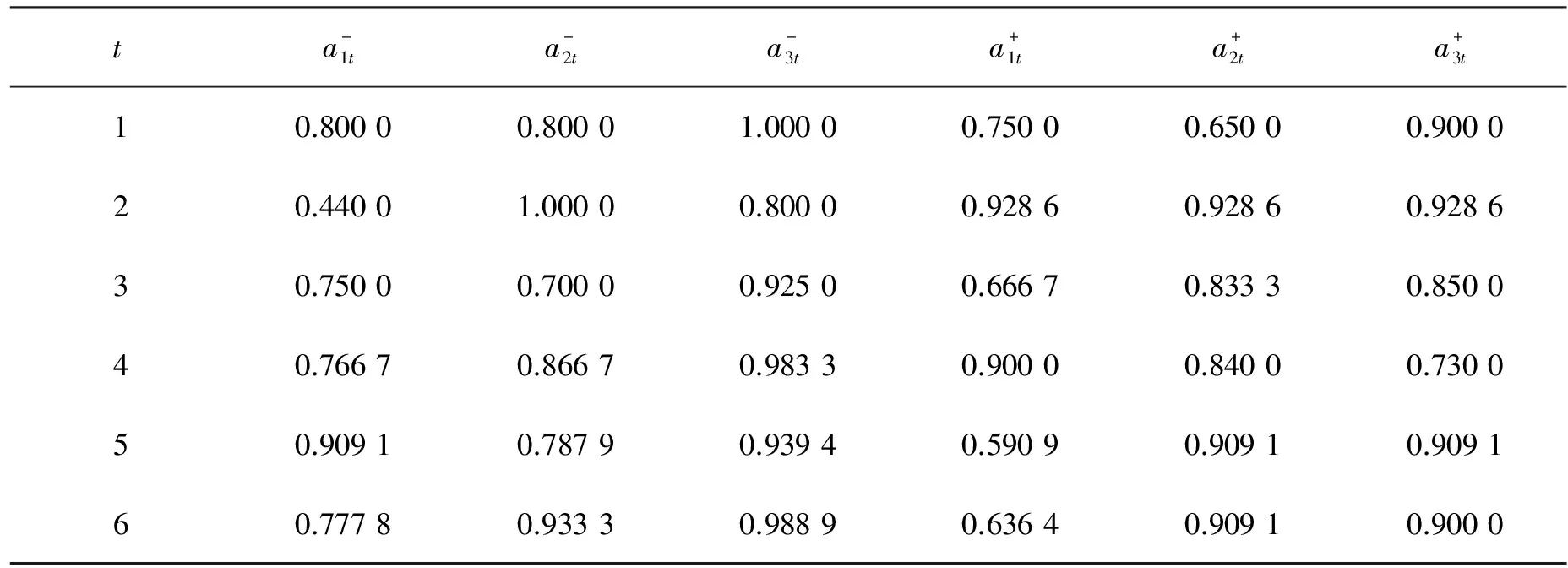
表2 各时刻单项预测值区间数的左端点精度、右端点精度
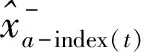
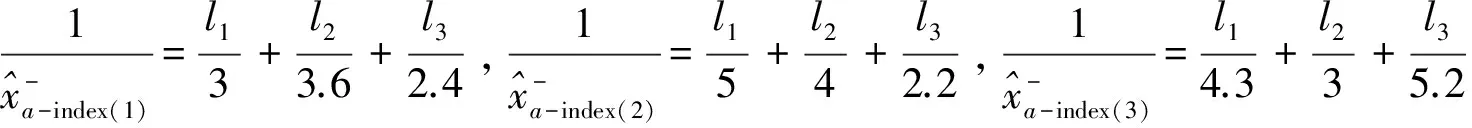

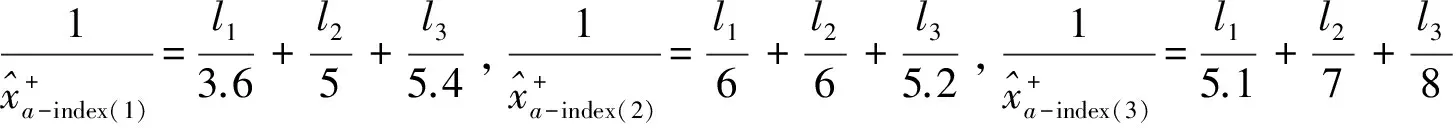
代入单目标最优组合预测模型(2),利用Lingo求解得出结果为:
k=0.2所对应的最优权向量为(0.561 7,0.343 2,0.095 1)T,
k=0.5所对应的最优权向量为(0.719 5,0.248 3,0.032 2)T,
k=0.8所对应的最优权向量为(0.851 1,0.148 9,0)T
进一步计算出不同k值下对应权重的组合预测值区间数,具体数据见表3.

表3 实际值区间数和不同k值下组合预测值区间数
采用定义2中的各误差指标作为评价指标,检验所提出的变权系数区间型组合预测方法的预测效果,具体数据见表4.
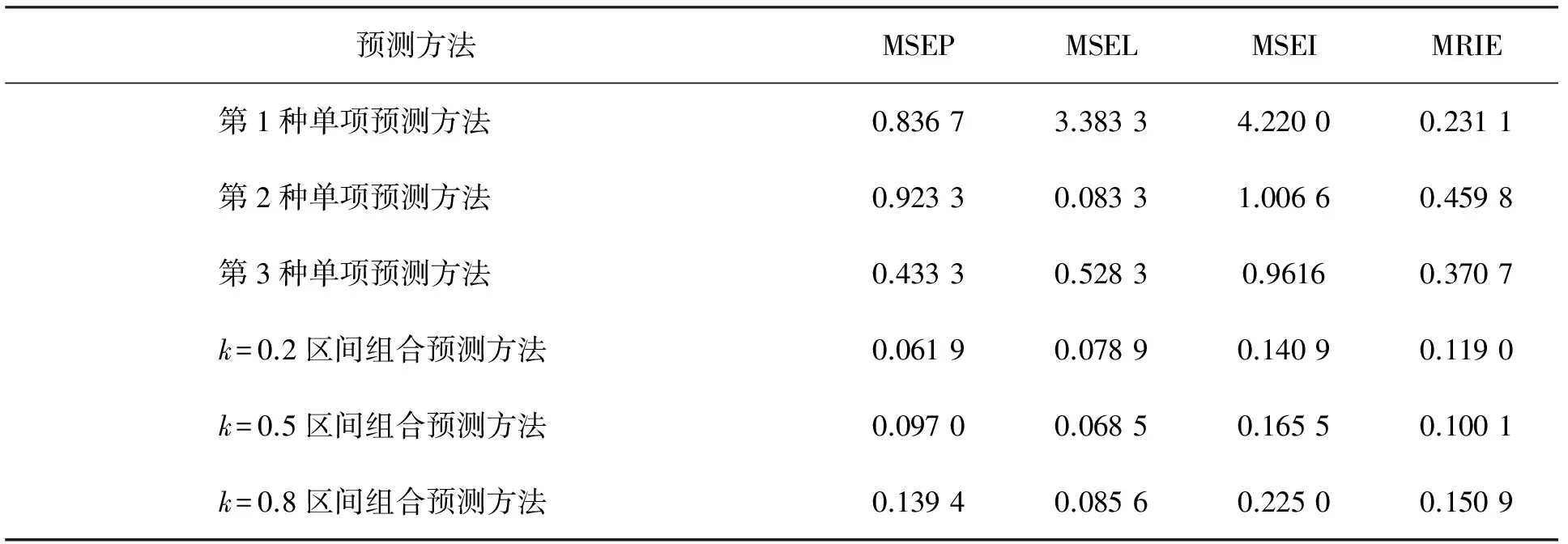
表4 各类预测方法的误差指标
表4中各误差指标显示,本文提出的区间型组合预测方法在各误差指标上都远远小于参与计算的三种单项预测方法的误差指标,同时对比文献[8~11]中提出各种区间型组合预测方法计算结果,发现本文的方法也是优越的,这些都显示提出的变权系数区间型组合预测方法是一种合理可行方法.
另外,根据定义7和定义8计算出不同的k值下各类区间数端点的倒数序列向量夹角余弦分别为:
k=0.2:γ1=0.990 4,γ2=0.995 4,γ3=0.997 5,而γ(l1,l2,l3)=0.999 0;
k=0.5:γ1=0.982 4,γ2=0.995 8,γ3=0.996 5,而γ(l1,l2,l3)=0.998 7;
k=0.8:γ1=0.974 4,γ2=0.996 1,γ3=0.995 6,而γ(l1,l2,l3)=0.999 2
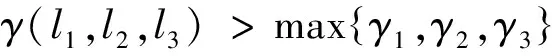
4 结语
由于客观世界中很多不确定性和不完备的问题,其中蕴含的信息可以用区间数来表示,对其开展的区间型组合预测方法是有必要和全新的研究课题.本文所提出的基于向量夹角余弦的IOWHA算子的区间型组合预测方法,是一种新的更精确的区间型组合预测方法,也是一种相关性指标准则下的变权系数最优区间型组合预测模型.文中定量模型建立以后通过实例分析的数据计算,表明是一种有效的区间型组合预测方法,但没有对该方法的有效性理论开展进一步的探讨,今后可对其进行深入的研究.
参考文献:
[1]Bates J M , Granger C W J .Combination of Forecasts[J].Operations Research Quarterly,1969,20(4):451-468.
[2]唐小我,马永开,曾勇,等.现代组合预测和组合投资决策方法及应用研究[M].北京:科学出版社,2003.
[3]王应明.基于相关性的组合预测方法研究[J].预测,2002,21(2):58-62.
[4]陈华友,刘春林,盛昭瀚. IOWHA算子及其在组合预测中的应用[J]. 中国管理科学,2004,12(5):35-40.
[5]袁宏俊,杨桂元. 基于最大—最小贴近度的最优组合预测模型[J]. 运筹与管理,2010,19(2):116-122,128.
[6]袁宏俊,陈华友,胡凌云.基于指数支撑度的最优组合预测模型及其性质研究[J]. 应用概率统计,2012,28(2):150-160.
[7]徐惠利,吴柏林,江韶珊.区间时间序列预测精准度探讨[J]. 数量经济技术经济研究,2008,12(1):133-140.
[8]张进,苗强,陈华友,等.最大误差绝对值达到最小的区间组合预测模型[J]. 合肥学院学报:自然科学版,2009,19(4):31-34.
[9]陶志富,张进,陈华友.基于向量夹角余弦的区间组合预测多目标规划方法[J]. 西华大学学报:自然科学版,2010,29(3):35-37.
[10]王晓,刘兮,陈华友,等.基于IOWA算子的区间组合预测方法[J]. 武汉理工大学学报:信息与管理工程版,2010,32(2):221-225.
[11]陈华友,李翔,金磊,等. 基于相关系数及IOWA算子的区间组合预测方法[J]. 统计与决策,2012,(6):83-86.
[12]胡凌云,袁宏俊. 基于左右端点的IOWGA算子的区间型组合预测模型[J]. 统计与决策,2013,(11):22-25.

