基于奇异强度理论的疲劳特性评估方法
高嵩,徐丽,Nigel BARLTROP,王大政
1 交通运输部水运科学研究院,北京100088
2 哈尔滨工业大学(威海)船舶与海洋工程学院,山东威海264209
3 斯特莱斯克莱德大学 船舶与海洋工程系,英国格拉斯哥G4 0LZ
0 引 言
各种类型的海洋工程结构在海上作业时,都会受到交变的波浪载荷作用,致使结构拐角节点处产生应力集中现象,萌生疲劳裂纹,最终造成疲劳破坏;因此,研究结构拐角节点处的应力集中至关重要。
考虑到应力集中程度取决于焊趾周边的结构尺寸,其函数形式并不明确,疲劳强度与垂直于裂纹扩展方向的法向应力场有关,法向应力场又忽略了每个尺寸下的应力增长和焊接的影响,所以大部分船级社规范都应用了S-N 曲线方法。虽然S-N 曲线法结合利用应力集中系数求取的计算应力可估算结构的疲劳寿命,但无法给出裂纹扩展时间历程。而基于断裂力学法的Paris 裂纹扩展法则能针对任意时刻给出裂纹扩展情况。Yung等[1]对应力集中最显著的结构(拐角过渡半径为0)进行研究发现,为求取实际应力分布,需要考虑焊趾或焊根处拐角半径尺寸的影响,否则,就要考虑应力奇异性(无穷大应力)。Maddox[2]和Gurney[3]为了在疲劳分析中考虑焊趾几何形状的影响,应用断裂力学方法,结合应力强度因子(SIF)求解了裂纹扩展率,同时针对实时检测缺陷和未被发现的假想裂纹缺陷问题,将疲劳应力应用于结构寿命评估。但是,由于微裂纹萌生时间较长、裂纹太小,因此,应用线弹性断裂力学方法分析疲劳裂纹扩展受到限制。为此,学者们研究了不同于断裂力学法和S-N 曲线的新方法,即切口应力强度因子理论(N-SIF)。
Williams[4]最早研究了裂纹尖端的应力场并得到了解析函数,此后,Gross 等[5]研究了N-SIF 理论并拓展了用来描述裂纹尖端应力场的SIF 定义,用其来描述V 型锋利角处的应力场。Lazzarin等[6-7]对不同构件进行定量分析,得到了应力场与结构尺寸相关的函数并加以验证,应用时,结果虽准确,但函数众多,参数选取复杂,计算繁琐。因此,高嵩和徐丽等基于N-SIF 理论,简化了结构拐角处应力函数及参数的选取,定义了“奇异应力函数”[8](见式(1)),引入了与结构尺寸相关联的奇异强度as 概念,同时,分别针对薄板直角结构和135°拐角结构给出了与结构几何尺寸的关系函数as=min(H/2,L/25)[9]和as=min[t(H/h)0.1/6,(2h+L)/8][8](式中:t 为受载板高,H 为非受载板高,L 为非受载板长,h 为肘板高,单位均为m,如图1 所示)。
式中:q=3p-0.5,p 取决于拐角处角度[4],其中,直角结构p=0.455,135°拐角结构p=0.326;x 为到拐角的距离;as 为表征奇异点特性的长度量(奇异强度);σn为均布拉伸名义应力,进而可求得本文所研究的135°薄板拐角结构(图1)中应力分析线上沿Y 方向的应力分布,并结合S-N 曲线进行疲劳特性分析。
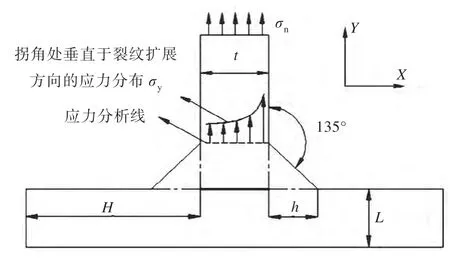
图1 受分析的结构边缘Fig.1 The edge of structure for analyzing
本文拟在上述研究的基础上,基于N-SIF 理论并结合S-N 曲线与线弹性断裂力学方法,给出通过由结构尺寸决定的奇异强度as 直接计算应力集中系数SCF 的方法。该方法将简化复杂参数的选取,并将考虑焊趾尺寸对拐角应力的影响,最终利用奇异强度即可直接计算SIF、应力集中系数SCF 及拐角处的节点应力,从而提供一种仅利用结构几何尺寸的简便方法。分析时,将采用ANSYS 数值模拟和MathCAD 数据拟合,最后得到本文“奇异强度理论”,希望能纳入船舶相关规范中做参考。
1 奇异权函数法
基于线弹性断裂力学,在结构拐角节点处萌生裂纹后,需确定临界裂纹尺寸、裂纹扩展速率及疲劳寿命,并依据断裂判据进行校核。因此,求解与其相关的SIF(单位:MPa·m1/2)至关重要。在应力场中,如果裂纹区域的权函数已知,那么裂纹扩展过程中的SIF 可见式(2)[10]:

式中:h(x,a)为取决于构件几何形状的权函数;σ(x)为无裂纹构件中沿预期裂纹扩展线的奇异应力分布,即式(1);a 为计算裂纹尺寸;x 为扩展线上节点至裂纹尖端的距离。
因此,只要得到权函数就可积分求解SIF。针对图1 所示的本文研究的135°薄板拐角结构,得到“奇异权函数”并以此计算SIF,此法命名为“奇异权函数法”。考虑到裂纹左边与肘板相连,可近似为半无限裂纹[11],裂纹右边可近似为边缘裂纹[12],可得到在裂纹两边均受载情况下,半无限裂纹的权函数近似于式(3)[11],边缘裂纹的权函数近似于式(4)[12],最终的奇异权函数利用上述两个权函数的平均值近似估算,简化后的结构如图2 所示。
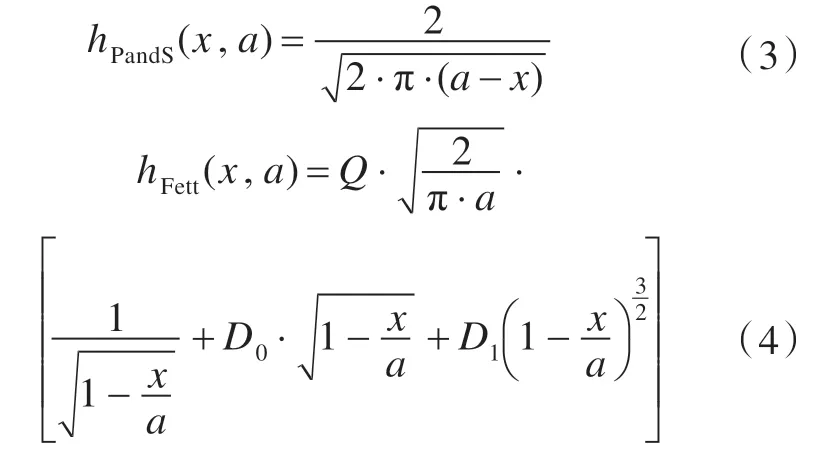
式中,D0和D1是基于无限小裂纹情况,利用Fett 权函数[12]进行取值,但考虑到结构的奇异性,在裂纹尺寸小于0.2 倍受载板高t(此例t=2 m)的条件下,需对式(4)进行修正(裂纹尺寸过大结构将失效),得到修正因子Q。分析发现,权函数式(4)是针对边缘裂纹而言,而边缘裂纹的形状系数Y=1.12 已知,因此可以直接利用边缘裂纹计算SIF 的一般公式拟合得到Q,结果见表1。

图2 拐角处裂纹权函数的近似法Fig.2 Weight function approximation of cracks at the corners
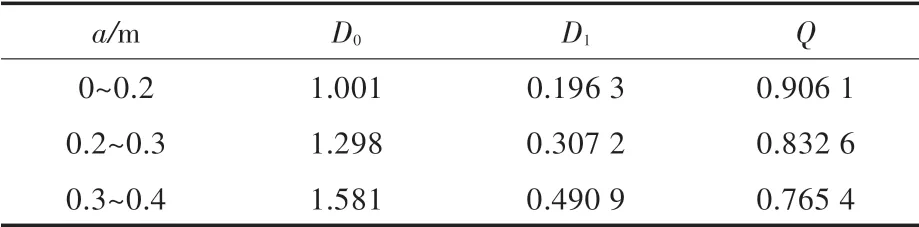
表1 权函数法下的参数选取Tab.1 Parameter selection under the weight function method
式(4)可进一步简化,舍去参数D0和D1,并直接修正得到式(5):

对比式(4)与式(5)计算的SIF(图3)发现,二者差别很小。
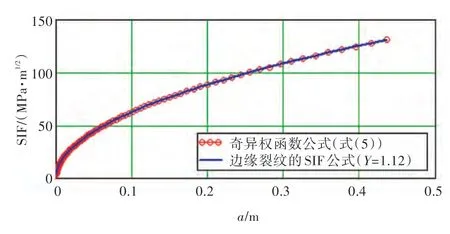
图3 奇异权函数公式与边缘裂纹的SIF 公式的结果比较Fig.3 Comparison of calculated SIFs by using singular weight function method and the edge crack SIF equation
最后,利用权函数式(3)与式(5)之和的平均值得到135°拐角处的权函数,见式(6)。

综上,在已知拐角处的奇异应力分布式(1),和奇异权函数式(6)后,可利用式(2)来求解SIF。图4 示出了用3 种不同的权函数计算的SIF,从图中可以看出,用奇异权函数法得到的SIF 介于用Fett 和Paris & Sih 权函数计算的SIF 之间,这是由于奇异权函数综合体现了裂纹上、下表面应力分布奇异性的结果。
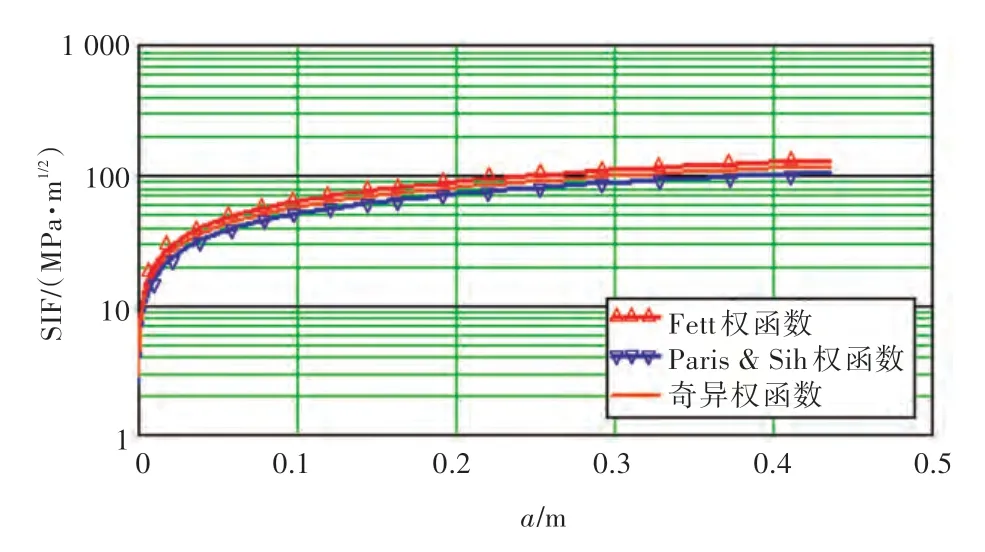
图4 各权函数计算的SIF 结果比较Fig.4 Comparison of SIF calculation results by using different weight functions
注意,如果以边缘裂纹计算得到的SIF 公式替代Fett 权函数修正式计算得到的SIF(Fett 权函数是针对边缘裂纹提出的),进而与Paris & Sih 权函数计算得到的SIF 求和取平均值,结果将出现较大误差,如图5 所示。这是由于本文奇异强度理论下的奇异权函数考虑了奇异强度影响下的奇异应力而进行积分计算,其表现了裂纹上、下表面应力分布的奇异性,但边缘裂纹计算的SIF 在无裂纹时,无应力集中。而在图1 所示的拐角节点处,即使裂纹不存在,仍旧存在应力集中现象,其应力就是本文的奇异应力,所以无法替代计算。

图5 边缘裂纹的SIF 公式替代结果比较Fig.5 Comparison of SIF alternative results for edge cracks
2 奇异等效裂纹法

图6 回归Y 值比较Fig.6 Comparison of regression Y values
考虑到135°拐角处的应力分布函数(∝1/r0.326)与裂纹尖端应力分布函数(∝1/r0.5)相近,且其他度数拐角结构与裂纹尖端也有相似性(∝1/rp)[4],故将拐角近似成一等效裂纹长度ae,并以此为参量来做相应的分析。这样,拐角处裂纹的计算长度a 为实际裂纹长度ac 与等效裂纹长度ae 之和,见式(7),同时应力强度计算见式(8)。

式中,σy可根据式(1)求得,通过回归,发现Y 与ae 将随着ac 而改变(表2),所以这样的公式形式也不易确定。为使奇异等效裂纹与奇异强度理论相关联,所以利用奇异强度as 来近似估算等效裂纹长度ae,并通过回归估算出Y=1 时ae=0.35as,从而得到奇异等效裂纹初始公式

式中,D=0.35。

表2 Y 与ae 准确的拟合结果Tab.2 Accurate fitting results of Y and ae
图7 显示了利用式(9)计算的SIF。由图中可看出,式(9)计算结果在一定范围内与ANSYS 结果拟合较好,误差小于5%,但越趋近于裂纹尖端差别越大,且ac=0时式(9)并未给出Kae=0。

图7 等效裂纹初始公式下的SIFFig.7 SIFs of equivalent crack under the initial formula
鉴于此,定义式(9)的适用范围(ac≥q·as),而对于小裂纹情况(ac<q·as),则需修正初始公式以满足ac=0 时Kae=0 的要求。因此,建立了实际裂纹y 轴与计算裂纹x 轴的关系曲线,并将实际裂纹用修正的as 替代进行分析,见图8。同时考虑建立幂函数曲线式(10),并认为其反函数式(11)是所需计算裂纹尺寸a 的最终解。


图8 裂纹关系分析Fig.8 Analysis of crack relationships
由图8 可知,在x=(D+q)·as 处y=q·as,故
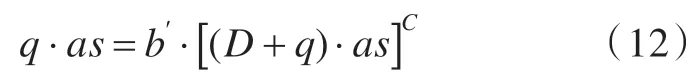
为保证修正曲线顺利过渡到临界值,得


这样就确定了小裂纹(ac<q·as)SIF 的修正函数式(15),及计算SIF 的奇异等效裂纹最终函数,即ac<q·as时采用式(15),ac≥q·as时采用式(9)。

式中:q=0.2;D=0.35。其既满足实际裂纹尺寸ac=0 时Kae=0 的要求,又保证了曲线过渡节点处数值相等且相切,如图9 所示。
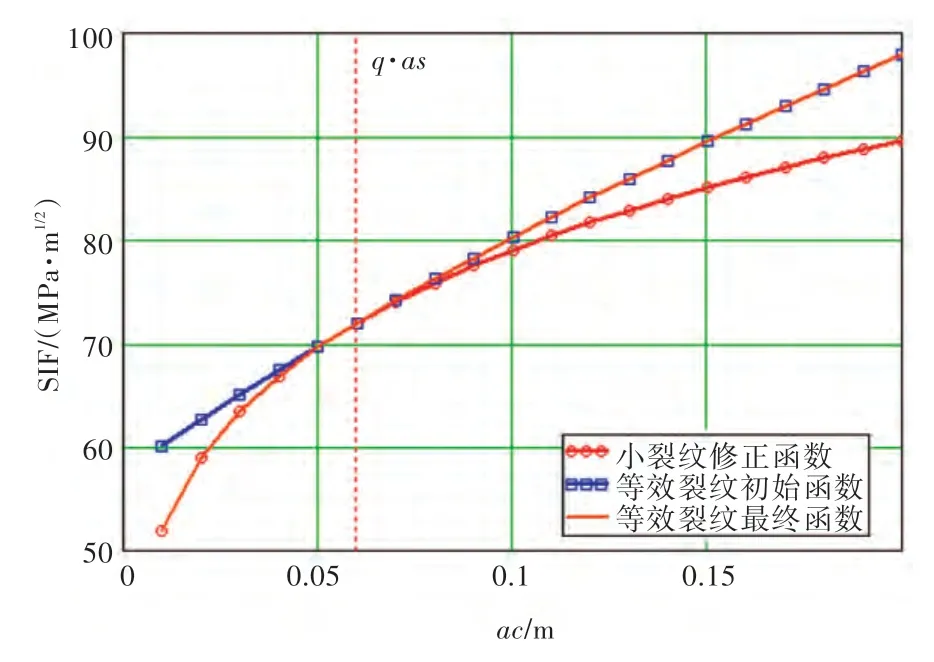
图9 等效裂纹函数分析Fig.9 Analysis of equivalent crack functions
图10 对应用不同方法计算出的SIF 进行了比较。结果显示:对于二维135°拐角结构,ANSYS的数值计算结果与奇异权函数法及等效裂纹概念的简化方法得出的结果拟合较好,远端最大差别均不超过5%,考虑到裂纹尖端网格划分的影响后,在无限趋近于裂尖处,差别均不超过10%,可见奇异权函数法和奇异等效裂纹法均可以保证一定的计算准确性,同时奇异等效裂纹法与奇异权函数计算的结果拟合度较高,进一步利用解析法验证了结果的可靠性。
3 奇异强度疲劳特性评估
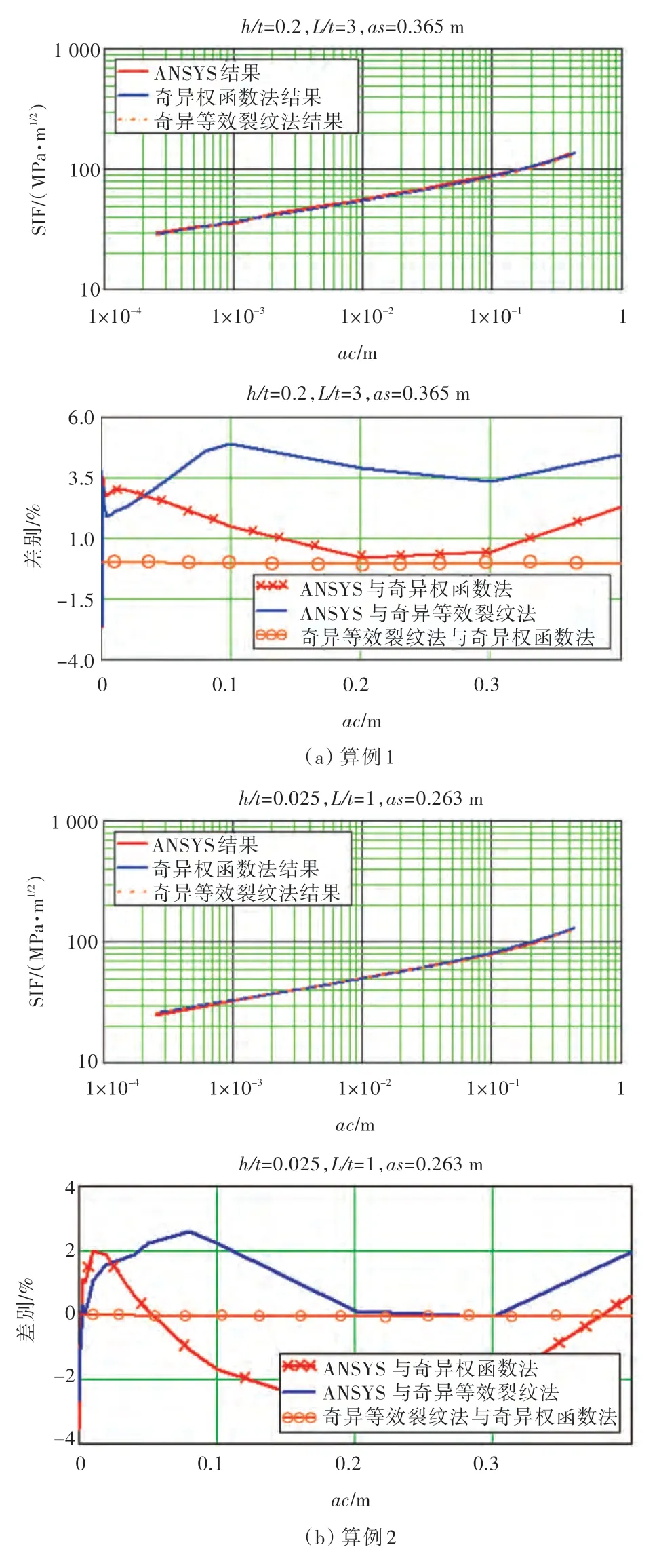
图10 计算SIF 的方法比较Fig.10 Comparison among different SIF calculation methods
实际应用中,通常将有限元分析结果与S-N曲线相结合来进行疲劳评估,并存在不同的疲劳应力分析方法。在名义应力法中,是将结构几何效应和焊接引起的应力集中都结合S-N 曲线进行分析,这样应力计算简便准确,但需要大量的试验才能确定S-N 曲线,成本很高。目前大部分船级社采用的热点应力法中,结构几何效应引起的应力集中被放入应力计算中考虑,并通过有限元分析得到结果,焊接引起的应力集中则仍放入S-N曲线加以分析,这样可减少试验次数,降低成本,但如何将几何效应和焊接引起的应力集中分离开较为复杂。而切口应力法中,结构几何效应和焊接存在引起的应力集中都是通过应力计算分析,试验最少并且只需得到材料的S-N 曲线。
这里的奇异强度as 是通过结构几何尺寸定义的,进而得到奇异应力[8],因此考虑了结构尺寸效应影响的应力集中,同时该理论也将结合S-N 曲线的试验结果(基于BS 7608 规范[13]选取材料参数m 和C,考虑了焊接引起的应力集中),进而分析得到“奇异应力集中系数”SCFas,其与名义应力之积即为拐角节点应力,从而满足了切口应力的定义。此外,由于Lazzarin 等[6-7]研究的N-SIF 理论针对的是切口应力,而这里的奇异强度理论是基于Lazzarin 等[6-7]的研究,同时对Williams[4]计算应力时复杂参数的选取进行了简化,并以奇异强度as 取而代之,所以也可以说是切口应力。在求得切口应力后,即可通过临界应力校核,或者继续分析得到应力强度因子并与材料的断裂韧性比较,分析是否满足结构强度。
已知S-N 曲线中的E 曲线可用于外载垂直于焊缝的没有结构奇异性的对接焊结构[13];因此,本文选其作为基准S-N 曲线,对于任何结构都将采用此基准S-N 曲线进行疲劳寿命分析,其中不同结构形式以及不同应力成分的影响将通过下文定义的SCFas来体现。
为了得到该SCFas,首先基于Paris 裂纹扩展法则[11]的断裂力学方法对结构进行疲劳分析,得到其疲劳寿命。然后,应用S-N 曲线中的E 曲线得到同样的疲劳寿命,为此,必须将结构的名义应力乘以一个应力集中系数,这样就可以确定不同尺寸拐角结构相应于此S-N 基准线(此处选取E 曲线)的应力集中系数,而不需要针对不同的结构形式选取不同的S-N 曲线。具体计算方法如下。
例如,图1 中的结构,as=0.2 m(as 定量,由H,h,L,t 计算),σn=100 MPa,实际裂纹尺寸ac 变化(0.25~267.95 mm),裂纹扩展方向受载板高t=2 m。在上述条件下采用奇异等效裂纹法分析疲劳特性,步骤如下:
1)已知高强度钢材料的断裂韧性KC=104 MPa·m1/2,计算临界裂纹尺寸aC=268 mm。
2)将应力幅值结合奇异等效裂纹法计算奇异应力强度因子幅值Δ Kas,由于Δ Kas=Kmax-Kmin,Kmax和Kmin是由疲劳循环过程中最大应力与最小应力计算得到,且脉动循环过程中最小应力习惯取0(无裂纹SIF 亦为0),所以ΔKas即Kmax,可利用奇异等效裂纹法计算,结果如图11 所示。
3)基于BS 7910 规范[14]要求,针对奥氏体(室温平衡基体组织)在内的钢材,选择暴露于空气中且非腐蚀良性环境下的相应参数,即A=5.21×10-13,m=3,并由式(16)计算裂纹扩展率,结果如图12所示。

4)由于ΔN=Δ a/(da/dN),因此可计算分析裂纹扩展到不同尺寸所需的循环次数(图13),并得到结构达到临界裂纹尺寸aC时结构的疲劳寿命Nae=323 433 次。

图11 应力强度因子幅值Fig.11 Stress intensity factor range

图12 裂纹扩展速率Fig.12 Crack growth rate

图13 裂纹扩展所需的循环次数Fig.13 Number of cycles required for crack propagation
若利用奇异权函数法进行分析,图14 给出采用了两种方法计算的裂纹扩展速率与疲劳寿命的比较结果,发现奇异等效裂纹法的裂纹扩展率较小,疲劳寿命较大。如果以此为标准并结合S-N曲线,则选取应力结果偏小(S-N 曲线应力与疲劳寿命成反比)。若以此为设计应力,则更易达到规范要求,这里采用奇异等效裂纹法分析SCF。

图14 等效裂纹法与权函数法疲劳特性结果比较Fig.14 Comparison of fatigue characteristics between equivalent crack method and weight function method
对于同一结构,如果应用S-N 曲线中的E 曲线来得到同样的疲劳寿命,则应力必须乘以一集中系数,这里定义为“奇异应力集中系数”SCFas,见式(17)。式中:Nae为通过Paris 裂纹扩展法[11]求解得到的结构疲劳寿命;σn为名义应力;常数m=3,C=1.04×1012,基于BS 7608 规范[13]选取;SCFas可根据以上已知量进行计算,见式(18)。

图15 给出了不同尺寸拐角结构(不同as 值)对应的E 曲线的SCFas。可以看出,SCFas与奇异强度成正比(奇异强度与结构尺寸相关)。这是因为结构尺寸较大时,奇异应力场高,应力区较大,裂纹扩展时间较长,扩展速度较快,结构的疲劳寿命变短,所以对应的E 曲线的SCFas就会变大。

图15 E 曲线的SCFas与as的关系Fig.15 Relationship between SCFas and as with E curve
为了更容易地确定SCFas,这里回归得到SCFas的计算式(19)。将计算结果与原始计算值进行比较(图16),发现拟合较好,最大差别小于3%。

式中:A=0.841 27;B=3.476 55/mm-C;C=0.374 23;as的单位为mm,SCFas为无量纲参数。

图16 拟合结果和原始计算所得SCFas的比较Fig.16 Comparison of SCFas between fitting results and initial calculations
这里介绍的SCFas是以S-N 曲线中的E 曲线为基准,即对任一具有奇异性的结构,如果知道as,即可应用图15 或式(19)得到与E 曲线相对应的SCFas,进而得到切口应力并与E 曲线结合查得疲劳寿命。
此外,在名义应力定性的前提下,也可得到结构疲劳寿命与奇异强度as的关系(图17)。
目前应用的S-N 曲线方法是基于结构的型式,结构的SCF 有时需要通过光弹性试验来获得。本文提及的SCFas既包含了结构奇异性的影响,也包含了不同结构型式的影响。通过与已知的S-N 曲线结果比较,直角结构估算的类似SCFas误差在5%以内,见表3[15],证明了该法的可行性。

图17 疲劳寿命与奇异强度关系Fig.17 Relationship between fatigue life and singular strength

表3 直角结构估算的类似SCFas的对比Tab.3 Comparison of similar SCFas for cartesian structure
4 切口应力等效取值法
以切口应力强度因子理论为背景,对Lazzarin等[6]求解的切口区域的应力场函数进行简化,得到奇异应力函数式(1)[8],进而变换为式(20),并定义“切口等效应力集中系数”SCFσ,同时将上述SCFas值等价于SCFσ来计算,进而利用奇异应力函数计算拐角处的切口应力。

由式(1)和式(20)可知SCFσ满足式(21)的关系,并可求得拐角处的切口应力(x=0)。但是,很明显,当x=0 时式(21)无解,所以只能在x→0 的前提下,以节点到拐角距离的近似值来等效x=0 的情况。例如,CCS 给出的热点应力外插法,就是采用0.5z 和1.5z(z 为板厚)的线性外插值作为拐角节点处的热点应力进行疲劳寿命分析。同时在已知的结构中,as 已知,SCFas等价于SCFσ,因此,只需求得节点到拐角处的距离x 便可利用式(1)得到切口应力,为此,定义了“切口应力等效取值点”xas。

这里,基于上节奇异强度疲劳特性评估方法回归得到取值点的位置xas,并利用最小二乘法拟合出切口应力等效取值点xas的分段函数式(22)。

式中:as和xas的单位为mm;A,B,C,D,E 见表4。

表4 切口应力等效取值点最小二乘法公式分段参数Tab.4 Segmentation parameters of squares formula for equivalent notch stress points
将式(22)得到的取值点位置与回归的“准确”值比较,见图18,发现取值点最大差别小于0.5%,拟合较好。同时将式(22)的结果代入式(21)计算SCFσ,并与SCFas回归的“准确”值比较,发现最大差别小于0.2%,见图18,结果较为准确。

图18 切口应力等效取值点及应力集中系数的比较Fig.18 Comparisons of singular stress concentration factors and equivalent notch stress points
同时,绘制了等效取值点xas与奇异强度的关系曲线,见图19。从图中可以看出:当as 较小时(as<1 m),等效取值点xas与板厚z 具有式(22)的关系,这是因为as 取决于结构几何尺寸,当结构尺寸较小时,as 决定拐角尖端应力场的强弱;但随着as 的增大,等效取值点收敛于0.4z(此系列板厚z=0.01 m),这是因为as 较大时,板厚相对于主体尺寸近似于无穷小并且对等效取值点的影响较大。所以,对本文奇异应力函数及奇异应力场集中系数SCFσ(式(21))而言,式(22)适用于as<1 m的情况,当as≥1 m 时,xas=0.4z。
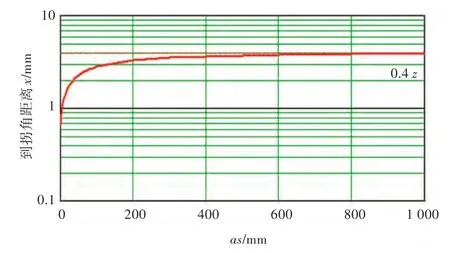
图19 回归得到的等效取值点Fig.19 Regression of equivalent points
值得注意的是,目前对于拐角处应力的近似,现有规范中常采用0.5z 和1.5z 的外插应力值作为拐角处的热点应力,也有的采用0.5z 处的应力值作为拐角处的热点应力,见图20。本文通过比较裂纹扩展法则计算的疲劳寿命与S-N 曲线计算的疲劳寿命得到的应力取值点xas=0.4z可做参考。

图20 拐角处应力分布及典型外插法的外插点位置Fig.20 Stress distribution of typical corners and extrapolation position
5 结 论
本文利用ANSYS 和MathCAD,基于切口应力强度因子理论对奇异强度理论进行了研究,通过对典型薄板结构拐角节点的应力集中、应力强度及结构的疲劳特性分析,得到以下结论:
1)利用权函数计算SIF 时,可将薄板结构拐角裂纹近似为半无限裂纹和边缘裂纹,进而修正相应的权函数,并将上述权函数之和的平均值作为“奇异权函数”进行积分计算,得到SIF,命名为“奇异权函数法”。其结果经与ANSYS 结果比对,差别小于5%。
2)考虑到拐角处的应力分布函数(∝1/rp)与裂纹尖端应力分布(∝1/r0.5)相近,可将结构拐角近似成等效裂纹,并定义“奇异等效裂纹”来修正计算SIF 的裂纹尺寸,同时通过小裂纹函数的修正得到“奇异等效裂纹法”。其结果经与ANSYS结果比对,差别小于10%。
3)利用上述得到的SIF 进行了结构疲劳特性评估,计算了应力强度因子幅值、裂纹扩展速率与疲劳寿命,同时得到了计算切口应力的“奇异应力集中系数”的关系曲线与函数式,误差小于3%,以便结合S-N 曲线进行疲劳评估。
4)基于切口应力强度理论,简化奇异应力函数,得到了“切口等效应力集中系数”,用以计算拐角节点的切口应力,与回归的“准确”值相比差别小于0.2%。同时,定义了“切口应力等效取值点”(xas=0.4z),与回归的“准确”值相比差别小于0.5%。最终,提出“切口应力等效取值法”,可供基于有限元分析的应力集中分析做参考。
[1]YUNG J Y,LAWRENCE F V. Analytical and graphi⁃cal aids for the fatigue design of weldments[J]. Fatigue and Fracture of Engineering Materials and Structures,1985,8(3):223-241.
[2]MADDOX S J. The effect of plate thickness on the fa⁃tigue strength of fillet welded joints[M]. Abington,Cambridge:Abington Publishing,1987.
[3]GURNEY T R. The fatigue strength of transverse fillet welded joints[M]. Abington,Cambridge:Abington Publishing,1991.
[4]WILLIAMS M L. Stress singularities resulting from var⁃ious boundary conditions in angular corners of plates in extension[J]. Journal of Applied Mechanics-Transac⁃tions of the ASME,1952,19(4):526-528.
[5]GROSS B,MENDELSON A. Plane elastostatic analy⁃sis of V-notched plates[J]. International Journal of Fracture Mechanics,1972,8(3):267-276.
[6]LAZZARIN P,TOVO R. A notch intensity factor ap⁃proach to the stress analysis of welds[J]. Fatigue and Fracture of Engineering Materials and Structures,1998,21(9):1089-1103.
[7]LAZZARIN P,LIVIERI P. Notch stress intensity fac⁃tors and fatigue strength of aluminium and steel welded joints[J]. International Journal of Fatigue,2001,23(3):225-232.
[8]高嵩,徐丽,王大政,等.基于奇异强度理论135 度薄板拐角的应力评估方法研究[J]. 武汉理工大学学报,2013,35(12):72-79.GAO Song,XU Li,WANG Dazheng,et al. Research of stress assessment for the 135-degree sheet corner based on singularity strength theory[J]. Journal of Wu⁃han University of Technology,2013,35(12):72-79.
[9]徐丽,高嵩,BARLTROP N. 存在奇异点的结构疲劳评估简单方法[J].船舶工程,2013,35(6):9-14.XU Li,GAO Song,BARLTROP N.Simple method of fa⁃tigue assessment for structure with singular point[J].Ship Engineering,2013,35(6):9-14.
[10]BUECKNER H F. Novel principle for the computa⁃tion of stress intensity factors[J]. Zeitschrift Fuer An⁃gewandte Mathematik & Mechanik,1970,50(9):529-546.
[11]PARIS P C,SIH G C. Stress analysis of cracks[J].Fracture Toughness Testing and its Applications,1965:30-81.
[12]FETT T. Stress intensity factors and weight functions for special crack problems[R]. Report FZKA 6025,Forschungszentrum Karlsruhe, 1998, Karlsruhe GmbH.
[13]Technical Committee WEE/44. Code of practice for fatigue design and assessment of steel structures[S].BS 7608,British Standards Institution,1993.
[14]Technical Committee WEE/37. Guide to methods for assessing the acceptability of flaws in metallic struc⁃tures[S]. BS 7910,British Standards Institution,2005.
[15]BARLTROP N, XU L. Comparison of SCFs based on singularity assessment and those implied by fatigue classifications[R]. Report to TWI:GSP/JIP16881,4th Sponsor Group Meeting,London,2008.

