模糊集和熵权法在船舶耐波性综合评价中的应用

王凯歌，屈俊飞，王鹏

1 海军驻大连船舶重工集团有限公司军事代表室，辽宁大连116005

2 中国人民解放军镇江船艇学院训练部，江苏镇江212003

3 海军蚌埠士官学校机械系，安徽蚌埠233012

0 引 言

在船舶性能评价方面，众多学者致力于构建使用方便且行之有效的船舶耐波性评价方法，期望对船舶的耐波性做出科学的综合评价，以指导船舶的论证设计和安全航行。然而，由于耐波性问题的复杂性，至今国际上关于船舶耐波性评价方法的研究还没有形成公认的实用方法。目前，对船舶耐波性进行综合评价的方法一般包括［1］：

1）船型参数表达法；

2）系统可靠性分析法；

3）运动状态记录分析法；

4）耐波性方程评估法；

5）单项指标评价法；

6）耐波性指标评估法。

其中，运动状态记录分析法可以反映船舶在不同装载、航行状态和风浪条件作用下的船舶运动特征响应，可较为真实、全面地评估单船或不同船舶的耐波性能，便于统计整理与比较分析，是一种实用性较强的综合评价方法。如粗糙集理论［2］、模糊数学方法［3］和BP 神经网络法［4-5］等的评价思想均源于运动状态记录分析法，近期，该方法已逐渐应用于高性能船舶的性能评价中。

本文将运用模糊集和熵权法［6］，选取若干组典型的船体运动状态记录数据构建船舶耐波性综合评价体系，以判断船舶耐波性能的优劣程度并对船舶耐波性能进行综合排序。该模型的数学原理简单、算法简便、计算量小、评估结果可靠，在船舶耐波性综合评价中具有较强的适用性。

1 船舶耐波性综合评价模型

1.1 综合评价指标体系

建立船舶耐波性综合评价模型，首先要确定影响船舶安全航行的耐波性因素，这些因素主要包括六自由度摇荡运动（纵荡、横荡、垂荡、横摇、纵摇、艏摇）的幅值、船体某横剖面垂向和横向加速度的幅值、艏底砰击、甲板上浪、螺旋桨出水、失速或增阻、晕船率和稳性的损失等。本文选取7个典型的耐波性因素建立船舶耐波性综合评价体系：横摇幅值、纵摇幅值、垂荡幅值、砰击概率、甲板上浪概率、螺旋桨出水概率，以及船艏垂向加速度幅值。在实际海况中，上述物理量可充分反映船舶在风浪扰动作用下航行时的运动响应特性，图1 为该综合评价体系的示意图。

图1 船舶耐波性综合评价体系示意图Fig.1 Integrated evaluation index system for ship seakeeping

1.2 指标归一化处理

若研究对象中的决策集共有n 个单元，可设定为W={W1，W2，...，Wn}；输入的指标数目为m，即A={A1，A2，...，Am}；并约定决策单元中的Wi对指 标 Aj的目标属性值为 zij（ i=1，2，...，n；j=1，2，...，m）；则综合评价中的决策矩阵可表达为Z=(zij)n×m，其表示决策集W 对指标集A 的属性值。

对船舶耐波性综合评价问题而言，评价指标可分为效益型指标、成本型指标、确定型指标和区间型指标［7］。此处，效益型指标指的是属性值越大越好的指标，成本型指标指的是属性值越小越好的指标，确定型指标指的是属性值为指定值的指标，区间型指标指的则是属性值以落在某个区间为最佳的一类指标。根据指标类型的不同，对指标集A 可做如下划分：

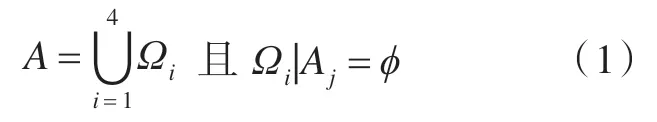
式中：ϕ 表示空集；Ωi(i=1，2，3，4) 分别为效益型、成本型、确定型和区间型指标集；j=1，2，3，4；i ≠j。

由于不同的评价指标其数学量纲不同，为消除量纲的不同所带来的不可公度性，在开展数学评价之前需将评价指标作归一化处理。显然，依据评价指标类型的不同，无量纲化方法也需相应改变。

对于效益型指标，一般可令

对于成本型指标，令

对于确定型指标，令

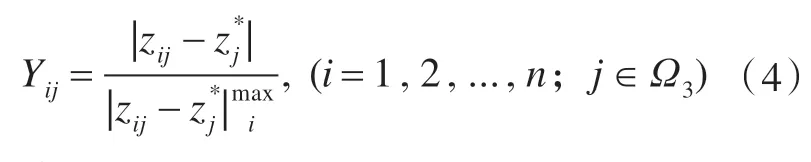
对于区间型指标，令

式中，[p1j，p2j] (i=1，2，...，n；j ∈Ω4) 为指标Aj的最佳稳定区间。

1.3 综合权重计算

由决策矩阵可知，各评价指标的熵值为Hj，即

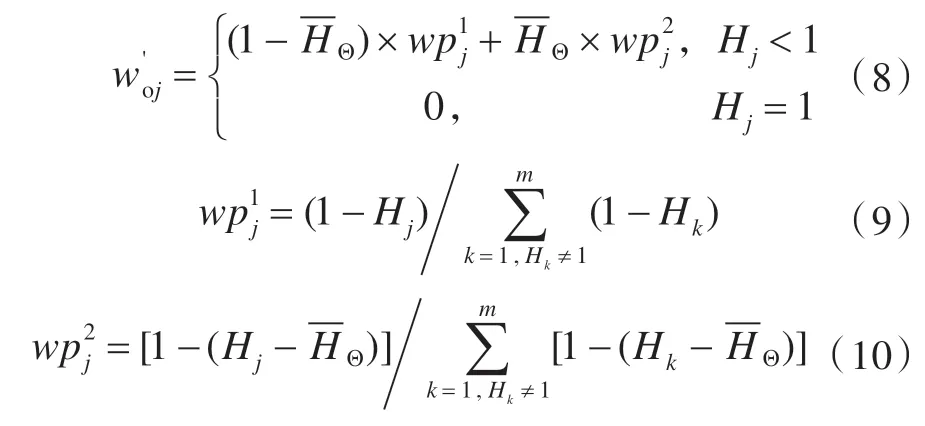
无论是主观赋权法还是客观赋权法，均存在一定的不足。为避免单一方法的缺陷，基于模糊集和熵权法的评价模型采用各个指标的综合权重，将由主、客观两种方法获得的指标权重有机结合起来。

本文运用一种加权平均数法［8］计算综合权重：

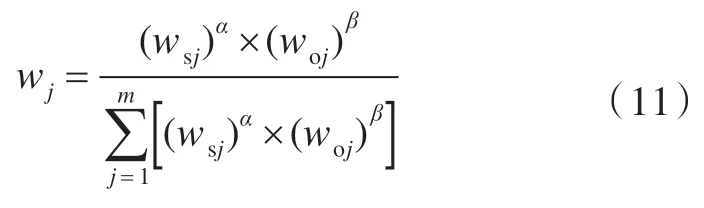
式中，α 和β 为主、客观权重在决策者心目中的比重，它可控制主观因素和客观因素对评价决策的相互影响。改进的综合权重确定方法能更加准确地刻画各属性在决策过程中的重要程度，其合理性更强。

1.4 评分函数求解

如果已知决策单元组成的决策矩阵是Y=(Yij)n×m，则正理想方案可表示 成，负理想方案可以表示成。 其 中，，。令Yij相对于正理想方案指标的模糊值为假定当时，Yij对于的真隶属度为，假隶属度为随着Yij逐渐远离逐渐变小，逐渐变大；当时，Yij对 于的真隶属度为，假隶属度为。定义Yij相对于正理想方案指标的真假隶属度计算方法为：

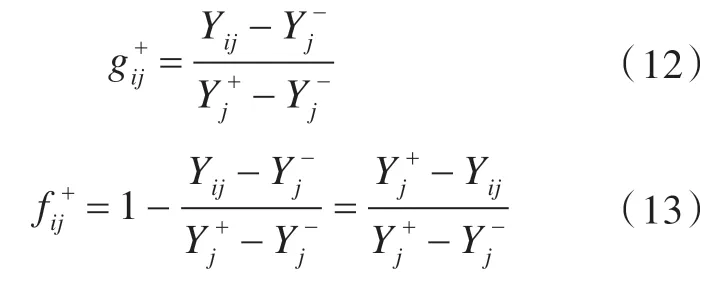
同理，Yij相对于负理想方案指标的真假隶属度为：

而当在决策问题时，接近正理想方案并不表示远离负理想方案。为此，考虑Yij相对于正理想方案和负理想方案的隶属度，并计算Yij相对于理想方案的综合模糊隶属度为：

结合各指标的综合权重，在综合模糊值矩阵T 的基础上，可确定各决策单元的综合模糊值Vi=[gi，1-fi]，且

而模糊值Vi的不确定度可定义为

各个决策单元相对理想方案的适应度可以通过以下评分函数计算得出：

经分析可知，g(Wi)∈(0，1)，f(Wi)∈(0，1)，故S1(Wi)∈(-1，1)，S2(Wi)∈(-1，0)。

评价各个备选方案的优劣，应先判断各个方案的S1(Wi) 评分的函数值，S1(Wi) 越大就表示该方案越优；若S1(Wi)相同，就再判断S2(Wi)评分的函数值，S2(Wi)越大则该方案越优。依据综合模糊值的物理意义也可以看出，当Yij更接近时，S1(Wi)为正；当Yij更接近Yj 时，S1(Wi)为负。

2 实例分析

2.1 数据输入

为校验上述评价模型在船舶耐波性综合评价中的可行性，选取某油船在风浪中航行时的运动状态记录数据［9］作为模型的输入，详细数据如表1所示。该油船的吨位为20 000 t，船长170 m，船宽25 m，吃水9.5 m，型深12.6 m。评价过程中用到的数据均来自实船试验，且样本数据涉及船舶在风浪中的30 个典型运动状态。表1 中，砰击、甲板上浪和螺旋桨出水均为概率指标值，砰击的指标值以100 次船体振荡中发生3 次记为0.03 作为参考，而甲板上浪和螺旋桨出水的指标值以每小时30 次记为0.05 作为参考。

2.2 评价指标权重值

基于MATLAB 平台，将反映船舶耐波性能的样本数据代入程序可获得决策矩阵。由于各指标均为成本型指标，归一化后的决策矩阵各元素为位于区间［0，1］的离散点，如编号11 的垂荡幅值归一化后的属性值为1.0，而编号12 的垂荡幅值归一化后的指标则为0。另外，决策矩阵的维度与初始方案集的维度相同。

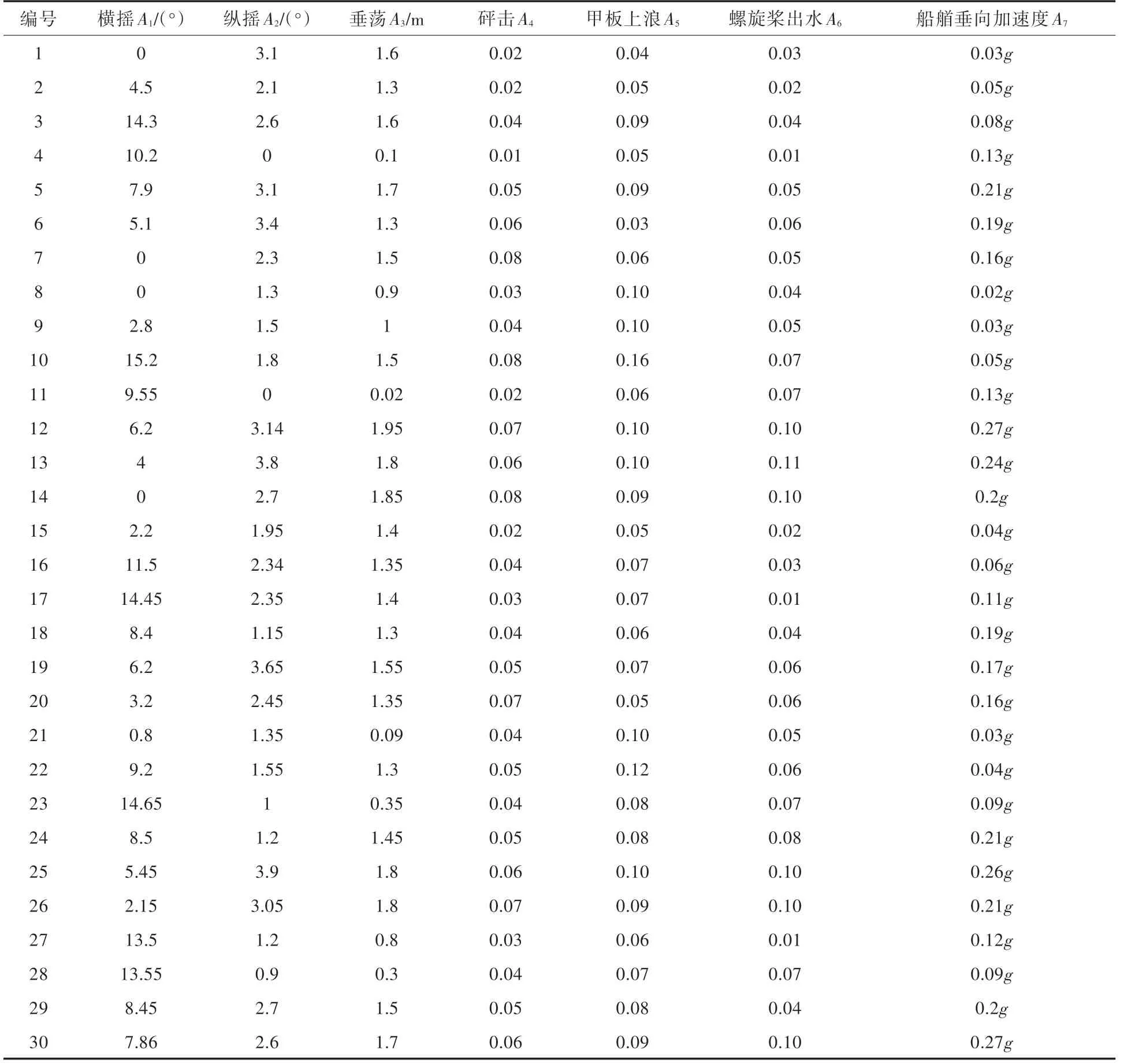
表1 样本数据汇总表Tab.1 Summary sheet of the sample data

依据模糊集和熵权法，可求解7 个耐波性评价指标的客观向量。在主观权重方面，由于横摇、纵摇、垂荡和船艏垂向加速度直接反映船体的运动姿态，故其权重相对较大；横摇的主观权重应比纵摇和垂荡较高，这一方面是由于横摇角的变化范围较大导致，另一方面，横摇幅值的大小与船舶的初稳性和大角稳性密切相关；从船体运动的合成分析可知，砰击和螺旋桨出水这2 个指标与船舶的纵摇和垂荡运动相关联，故其主观权重相对较小；另外，甲板上浪指标的主观权重相对较小，这是因为实际海浪为一平稳随机过程，除非海况的级别相差较大，否则甲板上浪的次数或概率不会发生较大的变化。依据各指标的重要程度及选取经验，7 个评价指标的主观权重值详见表2。

由表2 可知，各评价指标所确定的客观权重均在0.14～0.15 之间，这反映了决策矩阵中各列数据的内在差异不大。由耐波性理论可知，船体六自由度运动姿态对船舶耐波性的综合评价影响较大；相对于纵摇和垂荡，横摇运动这一指标更为突出，因为横摇幅值的大小与初稳性和大角稳性密切相关；从船体运动的合成分析可知，砰击和螺旋桨出水这2 项指标与船舶的纵摇和垂荡运动相关联，故其权重值相对较小；由于实际海况为一平稳随机过程，除非海况的级别相差较大，否则甲板上浪的次数或概率不会发生较大变化，因此甲板上浪指标的权重值相对较小。

表2 耐波性评价指标的加权向量Tab.2 Weight vector of seakeeping evaluation index

2.3 模型验证与分析

依据式（22）可得到船舶耐波性的综合评价值，表3 为采用本文数学模型计算得到的综合评价值，由1.4节的相关公式可知取值范围为（-1，1），表中还列举了安全评估结果。需指出的是，这里的安全评估值由船舶耐波性综合评估方程确定，即其采用的是耐波性方程评估法。

表3 各状态下的综合评价值与安全评估值Tab.3 Integrated evaluation and safety assessment values in different conditions

为分析模糊集和熵权法的评价结果与安全评估值的差异，图2 给出了采用两种不同方法评价的排序结果对比图。由图可知，运用本文数学模型进行船舶耐波性综合评价与采用综合评估方程评价船舶耐波性可获得十分相近的结果，这表明模糊集和熵权法应用于船舶耐波性综合评价是可行且有效的。其中，编号为4，8 和21 状态的耐波性综合评价结果相对靠前，查阅原始记录数据发现，这些编号下的部分运动数据为零；而编号为10，12，13 和25 状态的耐波性综合评价结果相对靠后，如编号10 状态下的横摇幅值为15.2°，为原始记录数据横摇幅值的最大值。

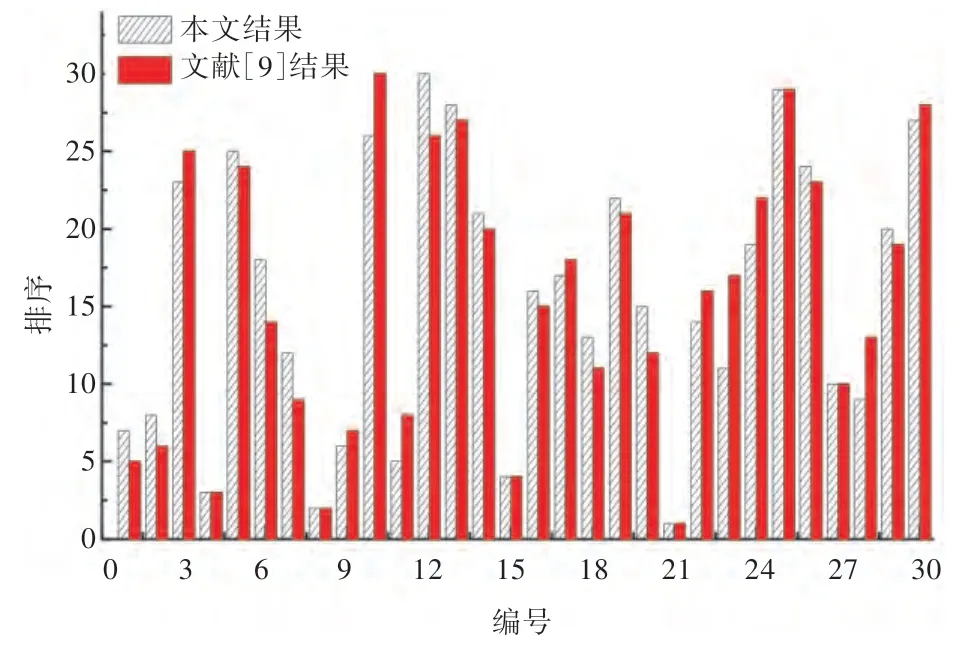
图2 本文模型与耐波性方程评估法的排序结果对比Fig.2 Comparison of the sorted result between proposed method and seakeeping equation assessment approach

3 结 语

模糊集和熵权法结合了客观赋权法和主观赋权法的各自特点，依据输入指标的数据矩阵提取备选方案中的有效隐含信息，并可反映评价对象所处的背景条件和评价者的意图，其综合权重的确定过程较为全面与成熟。

实例分析表明，本文所提出的数学模型可定性和定量评价船舶的耐波性能，在实际应用中具有一定的实用价值。

［1］熊云峰. 基于灰色系统理论的船舶耐波性综合评价研究［D］.武汉：武汉理工大学，2005.

［2］齐壮. 渤海湾客滚船大风浪中航行的耐波性综合评估［D］.大连：大连海事大学，2010.

［3］肖袁根，眭爱国，侯小军，等.基于模糊数学法的舰船耐波性综合评价［J］. 中国造船，2011，52（1）：235-244.XIAO Yuangen，SHUI Aiguo，HOU Xiaojun，et al.Comprehensive evaluation of seakeeping quality based on fuzz analyses［J］. Shipbuilding of China，2011，52（1）：235-244.

［4］李生长，李勇. BP 神经网络建立船舶耐波性评价的GUI实现［J］.科技创新导报，2012（25）：9-10.LI Shengzhang，LI Yong. The GUI realization of the evaluation model of ship's seakeeping by applying BP network［J］. Science and Technology Innovation Her⁃ald，2012（25）：9-10.

［5］李生长，王凤武，刘强，等. 基于BP 神经网络的船舶耐波性评价［J］. 大连海事大学学报，2012，38（1）：15-17.LI Shengzhang，WANG Fengwu，LIU Qiang，et al.Sea⁃keeping evaluation based on BP neural network［J］.Journal of Dalian Maritime University，2012，38（1）：15-17.

［6］AEYELS D，PEUTEMAN J. A new asymptotic stabili⁃ty criterion for nonlinear time-variant differential equa⁃tions［J］. IEEE Transactions on Automatic Control，1998，43（7）：968-971.

［7］QU J F，BI Y，XIAO W B. Integrated evaluation of ship maneuverability based on the method of maxing deviation［J］. Advanced Materials Research，2012，524：3888-3895.

［8］孔峰. 模糊多属性决策理论、方法及其应用［M］. 北京：中国农业科学技术出版社，2008.

［9］李生长. 油船大风浪航行中的耐波性评价研究［D］.大连：大连海事大学，2011.