基于鲁棒性的船体中横剖面多目标优化

彭清风，王德禹，王红霞

上海交通大学海洋工程国家重点实验室，上海200240

0 引 言

鲁棒性，是指目标函数对于解的设计参数或环境参数微小变化的不敏感性，即当解的设计参数或环境参数有较小的变化时，变化后的点仍属于可行解，且相应的目标函数值的变化量未超出许可范围。自1978年日本的田口博士提出鲁棒设计思想以来，鲁棒性设计在钢铁、汽车和控制等工程领域得到了广泛应用，产生了巨大的经济效益。

虽然鲁棒性思想已被广泛应用于许多领域，但其在船舶领域内的应用却并不多。周继胜和张圣坤［1］将自适应步长搜索法与鲁棒设计相结合，以客船为研究对象，以甲板纵桁屈曲和中内龙骨屈曲失效模式对材料弹性模量与板厚的变异系数为目标函数对结构进行了鲁棒性优化设计；于利磊等［2-3］提出了基于理想点法的双目标鲁棒设计；程远胜等［4-6］针对不确定量，对不符合概率性分布的情况做了大量研究；骆伟等［7］以主甲板处的最小剖面模数对主甲板的厚度的偏导数最小为目标函数，对浮式生产储油船的中横剖面进行了基于鲁棒性的优化设计；Diez 和Peri［8］提出了一种基于不可控变量的散货船鲁棒优化的概念设计，给出了鲁棒设计的一般数学表达式，约束采用最坏情况分析法，最后将其与粒子群算法相结合。

但是，作为大型复杂结构，船体结构特性和载荷响应若采用经验公式则过于简单，无法精确考虑结构各部分之间的相互影响和局部特性，因此，有必要采用有限元方法进行船体结构分析，精确分析其结构特性和结构响应，并将其作为船舶结构优化中的目标函数或约束特性值。本文拟将鲁棒优化的思想与有限元分析相结合，提出一种基于高精度近似模型的多目标粒子群优化算法，利用多目标优化中的Pareto 思想，将鲁棒性优化问题转化为两个子目标优化问题，即优化问题的最优性和鲁棒性。并以一艘多用途船为优化对象，选取多用途船的横剖面尺寸作为离散设计变量进行鲁棒性优化，然后将结果与传统的确定性优化结果进行对比，以验证所提方法的有效性。

1 结构鲁棒性优化设计原理

鲁棒性优化的一般描述如定义1。

定义1：鲁棒性优化问题。

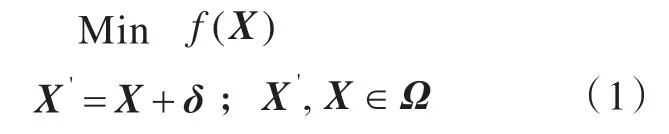
鲁棒性优化的目的就是寻找X'，以使式（1）达到最优。式中：X=(x1，x2，x3，…，xn)，为决策向量，其中Ω ∈Rn， Ω为可行空间 ；δ=(δ1，δ2，δ3，…，δn)，为扰动向量，其中n 为决策向量的维数。

定义2：鲁棒最优解。

鲁棒性优化的鲁棒最优解包含两方面的含义：鲁棒性（Robustness）和最优性（Optimality），

因此，鲁棒性优化问题实际上是多目标优化问题。 它可以描述为：

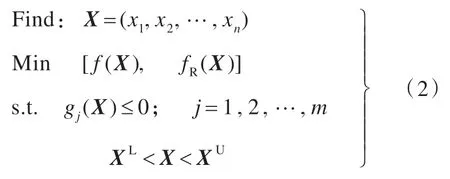
式中：f（X）为解的最优性；fR（X）为解的鲁棒性；X，XU和XL分别为设计变量及其上、下界；gj（X）为m 个约束中的第j个约束。

解的鲁棒性通常可以采用蒙特卡罗积分在解的附近进行抽样，用样本的平均值近似表示出鲁棒性函数。具体表示如下［9］：

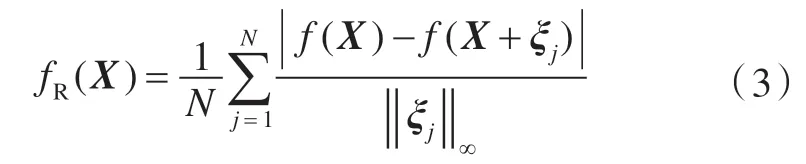
式中：ξj为第j 个样本；N 为样本的规模。

在实际生产中，受各种因素的影响，板厚和梁截面尺寸等结构参数均呈概率分布，因此对基于鲁棒性的船舶结构中剖面结构优化而言，决策向量即为结构的纵向板材板厚和梁截面尺寸等结构参数。而鲁棒性优化设计的目标则为在鲁棒性最佳与解最优之间寻求折中的结构性能函数，例如，结构重量或在一定载荷下的应力等。

2 优化算法的基本原理

2.1 粒子群优化算法

粒子群优化（Particle Swarm Optimization，PSO）算法是一种新的全局优化进化算法，最早被应用到设计变量为连续型的优化问题中。其位置和速度更新公式为：

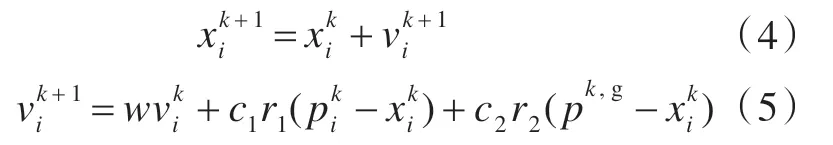
式中：xi为第i 个粒子的位置；vi为第i 个粒子的速度；k 为迭代次数为粒子i 直至第k 次迭代的历史最优位置；pk，g为所有粒子直至第k 次迭代的历史最优位置；w 为惯性权重；r1，r2为介于［0，1］之间的随机数；c1，c2为学习因子。

受工程制造的标准化等方面的限制，船舶的板厚等结构参数均取离散值，因而中剖面结构优化从本质上来说就是一种离散变量优化问题。对离散设计变量优化问题而言，其算法需要在每次迭代之后对位置取整［10］，即其速度更新公式与式（5）相同，位置更新公式修改为下式：

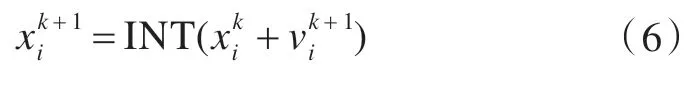
2.2 支持向量机概念

支持向量机（Support Vector Machine，SVM）是由Vapnik 等［11-12］首先提出的一种新型机器学习方法。支持向量机最初应用于模式识别工作，后来引入“不敏感损失函数”，发展出用于函数估计的支持向量回归（Support Vector Regression）方法。下面，将简要介绍支持向量回归方法的基本原理。

给定样本集D={(xi，yi)|i=1，2，···，l}，其中：xi∈Rn，为n 维输入样本；yi∈R，为输出样本。支持向量回归的目的是通过训练样本，用回归函数f(x)=wx+b 拟合输入样本与输出样本之间的关系，考虑允许拟合误差，引入非负松弛因子ξi和将函数的拟合问题转化为优化问题：

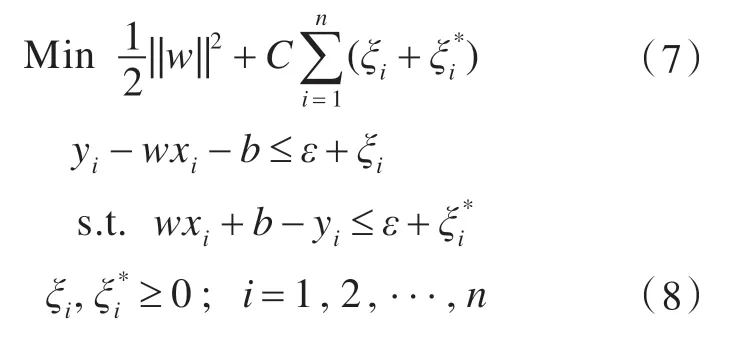
式中，C 和ε 为控制逼近函数VC 维的自由参数。

利用最优化方法的对偶原理，可以转换得到对偶形式为：

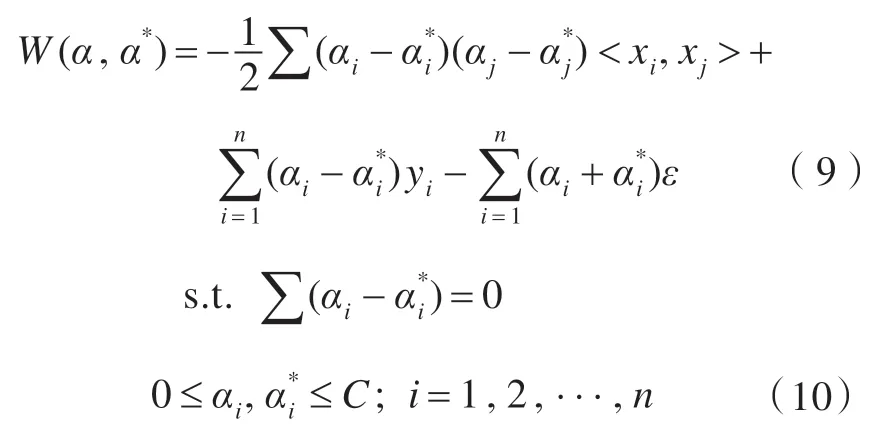
式中，α 和α*为拉格朗日乘子。

由式（9）和式（10）可以得到支持向量机拟合函数为

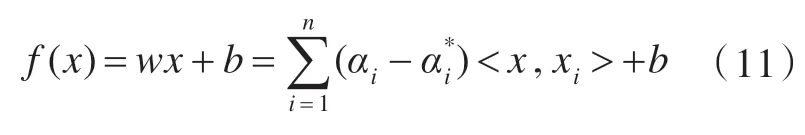
非线性回归使用非线性映射，将数据映射到高维特征空间进行线性回归，在高维特征空间用核函数替代线性问题中的内积运算，即

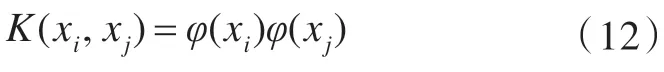
最后得到的支持向量机拟合函数为

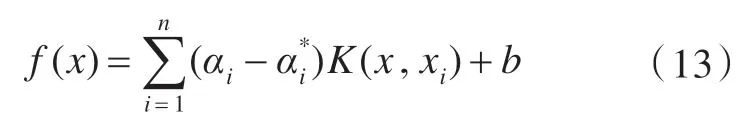
2.3 优化过程

将以上方法相结合，针对设计变量均为离散型的特点，本文基于MATLAB 软件编写了一种搜索鲁棒最优解的多目标粒子群优化算法。其具体算法如下：

1）初始化粒子群，将初始位置作为每个粒子的历史最佳pi。

2）计算每个粒子的目标函数值，并将目标函数值作为适应度值。本文采用蒙特卡罗积分原理，在每代中每个粒子的每一维的±5%区间进行均匀取样，得到100 个样本值，利用式（3）构造出了每个粒子的鲁棒性函数fR(X)。

3）筛选粒子群中的非劣解放入精英群中。当迭代次数小于最大迭代次数时：

（1）按照式（5）和式（6）对速度和位置进行更新，若某一维超过了边界，则重新对该维进行初始化；

（2）以一定的几率对当前粒子的所有维进行变异处理，然后依据第2）条得出目标函数值及适应度值；

（3）筛选本次迭代结果中的非劣解集，并将其与之前的非劣解集合并；

（4）对合并得到的非劣解集进行筛选，得出新的非劣解集；

（5）从非劣解集中挑选出相对较优的非劣解放入精英集中。本文中，控制精英集的个体数不超过40。

4）从最终的精英集中挑选出符合实际需要的鲁棒性最优解。

图1 所示为粒子群优化算法的基本流程。

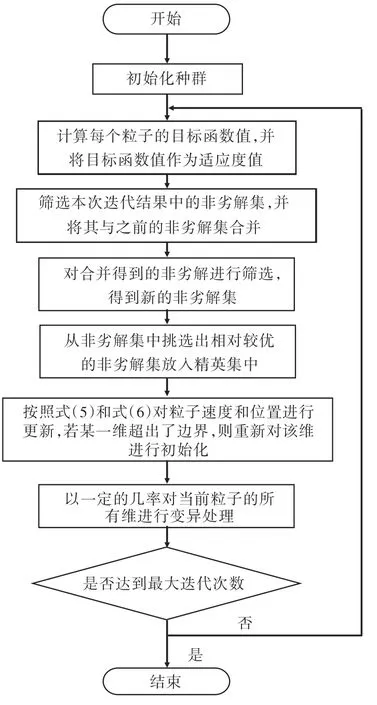
图1 粒子群优化算法基本流程Fig.1 Basic process of PSO algorithm

3 多功能船的中剖面鲁棒性优化

3.1 多功能船的主要参数

本文研究所建立的模型为618TEU 多用途船货舱区域的一个舱段，此多用途船主要装载集装箱和矿石等散装货物，船总长132.9 m，型宽19.3 m，型深9.9 m，设计吃水7.4 m，航速12 kn，共3 个货舱区域。舱段所受载荷及约束均根据船舶参数和载货情况按照《中国船级社散货船结构强度直接计算指南》确定。

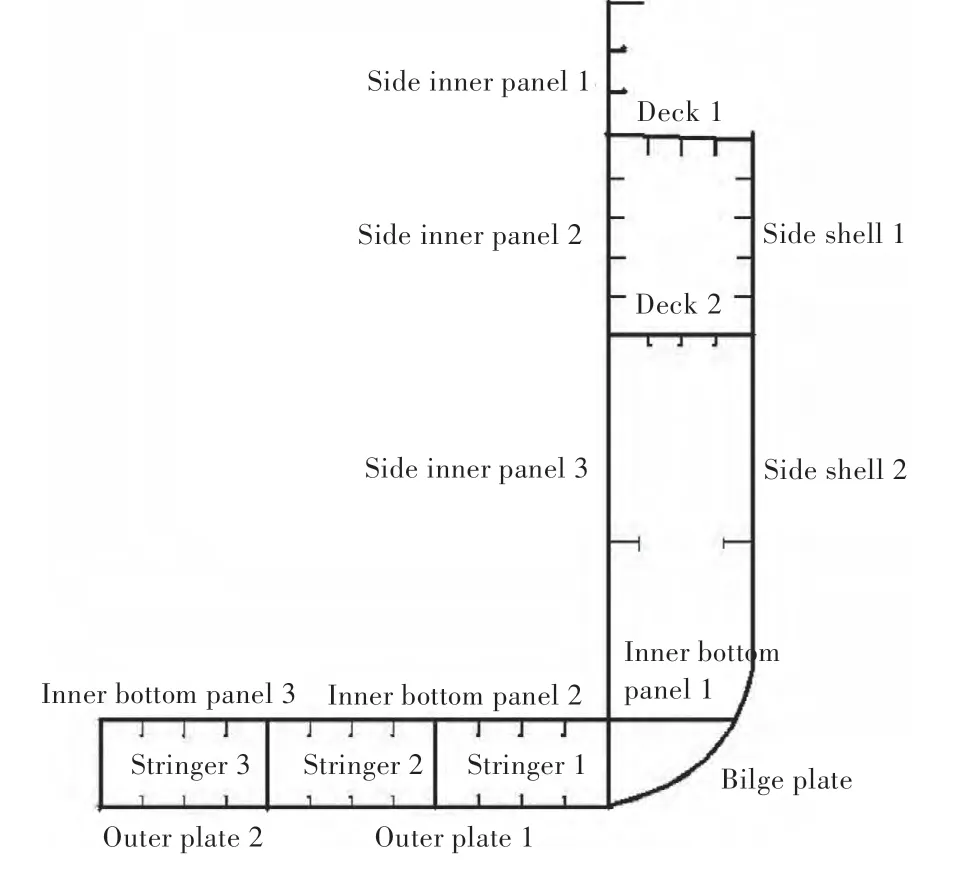
图2 设计变量分布图Fig.2 Distribution of design variables

3.2 设计变量

考虑到船体板对船体强度和船体重量的影响较大，同时船体纵向骨材较多，为简化问题，本文将主要探究船体板厚尺寸不确定性的影响。取中剖面中板的厚度为设计变量，每种板材以其原始厚度为中心，步长为1 mm，取5 种离散厚度作为设计变量的取值范围，板厚设计变量共16 个，而骨材的尺寸和间距则作为已知量。设计变量的基本信息如表1 和图2 所示。

3.3 约束条件

当约束条件为板的中面应力和梁的轴向力时，均需小于许用应力。依照规范选取，对板和梁分别按许用应力大小进行归类，共得到6 个约束条件，同时，控制船体的总重量不得超过设定的值。令每次有限元计算所得的应力值与许用应力值之差为g(X)，与总重量和设定的总重量的值之差为m(X)，即要求

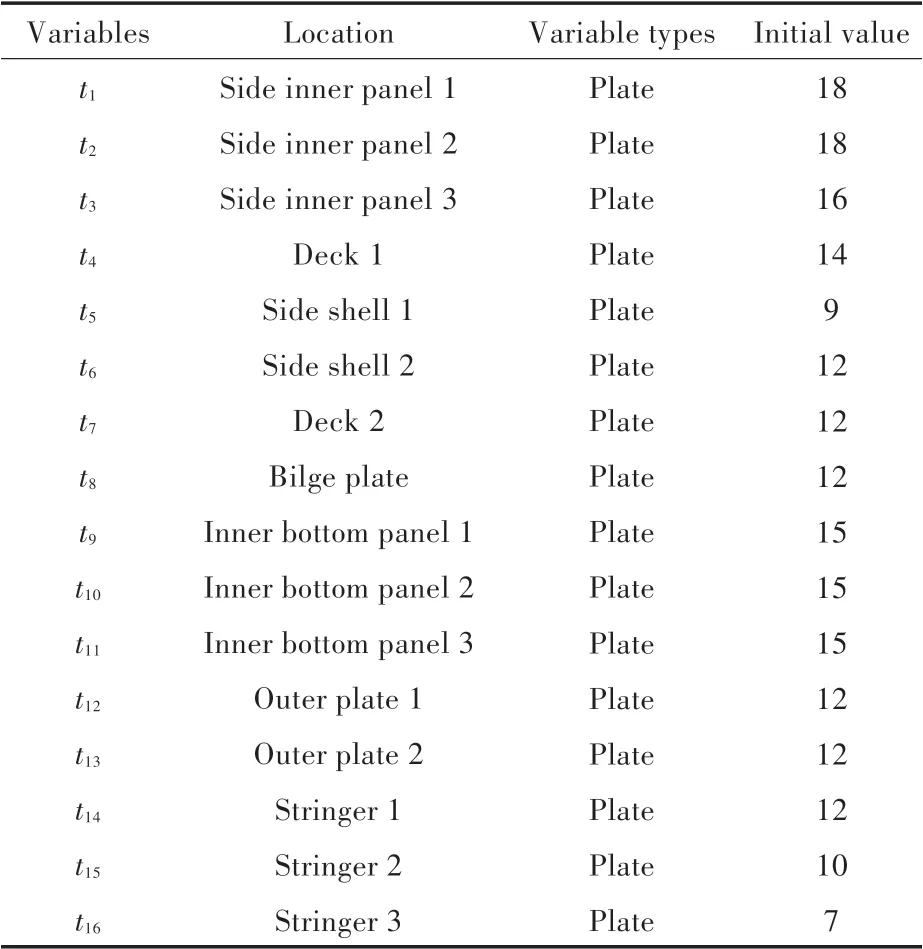
表1 设计变量信息表Tab.1 The information table of design variables

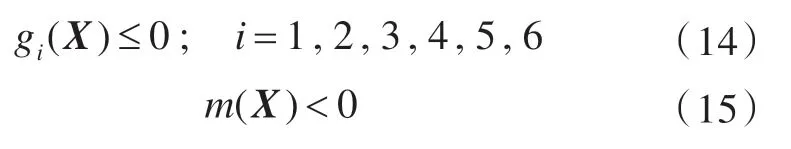
在程序中，对上述违反约束的情况将通过罚函数的形式表现出来。

3.4 目标函数

根据前期的分析，得出该舱段的最大应力非常大，且非常接近于许用应力，而由于生产误差和腐蚀老化的影响，易导致板厚的尺寸偏离初始设计值，板厚尺寸的变化将直接影响舱段的最大应力值，甚至有可能会出现最大应力值变大超出许用应力的情况。为了降低最大应力对板厚尺寸变化的敏感性，选择将最大应力值fσ(X)和与其对应的鲁棒性函数fR(X)作为多目标优化的目标函数。即

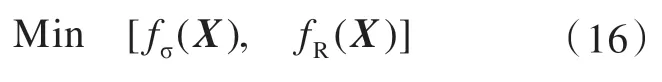
3.5 支持向量机近似模型

在求解本次优化问题时，每次迭代都需要进行长时间的有限元分析，以获得目标函数值和约束特性值。为了提高效率，可以建立结构的近似模型，以代替有限元分析进行优化设计。为了建立支持向量机近似模型，需要采用有限元分析获取一定数目样本的输入—输出关系。有限元分析由Isight 驱动MSC.Patran 修改模型，驱动MSC.Nastran 自动计算。采用拉丁方法收集2 100 个样本点，前2 000 个样本用来建立支持向量机近似模型，后100 个样本用于检验近似模型的精度，计算检验样本有限元分析值与支持向量机近似值的相对平均误差（Relative Mean Error，RME）。近似模型的精度分析结果如表2 所示。

表2 近似模型精度分析Tab.2 Precision analysis of approximation model

从表2 中可以看出，近似模型的精度较高，可为下一步的优化提供良好基础。

3.6 基于鲁棒性的优化设计结果

本次优化基于支持向量机近似模型与多目标粒子群优化算法，设置迭代次数为50 次。其中，每代粒子数目取为50，采用惯性权重递减的策略，初始惯性权重为0.9，最终惯性权重为0.4，变异的几率设为5%。一共得到了40 个Pareto 最优解，Pareto 解用散点表示在图3 中。通过分析，从以上非劣解前沿曲线中选择5 组设计方案作为鲁棒最优解，对应的目标函数以及设计变量的结果如表3 所示。最后，采用传统的粒子群优化设计方法对船体结构分别进行以船体总重量和最大应力为目标的单目标确定性优化，其优化结果亦如表3 所示。其中，Mopt表示以船体总重量为目标函数的单目标优化结果，Sopt表示以最大应力为目标函数的单目标优化结果。

由表3 中的各优化方案可以看出，经过鲁棒性优化设计后，中横剖面的鲁棒性能变得更好，舱段的最大应力对设计变量的敏感性均有较大程度的降低，特别是方案5 的鲁棒性得到了极大的提高，同时，各个方案的最大应力相对于初始设计值也有所减小。另外，值得注意的是，经过以上5 种优化设计方案优化后，得到的船体总重量相对于初始设计的船体总重量也有少许的减小。然后，通过评估传统单目标优化方法得出的优化结果可以知道，和前面的5 种设计方案相比，船体中剖面的鲁棒性变得较差，舱段的最大应力对设计变量很敏感，容易发生最大应力超出许用应力的情况。总体而言，以上5 种方案的优化效果均较明显，达到了优化目的。

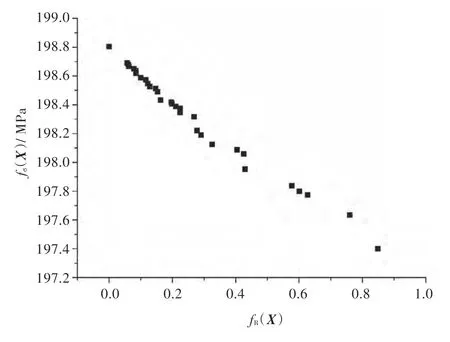
图3 Pareto 解集图Fig.3 Pareto solution sets

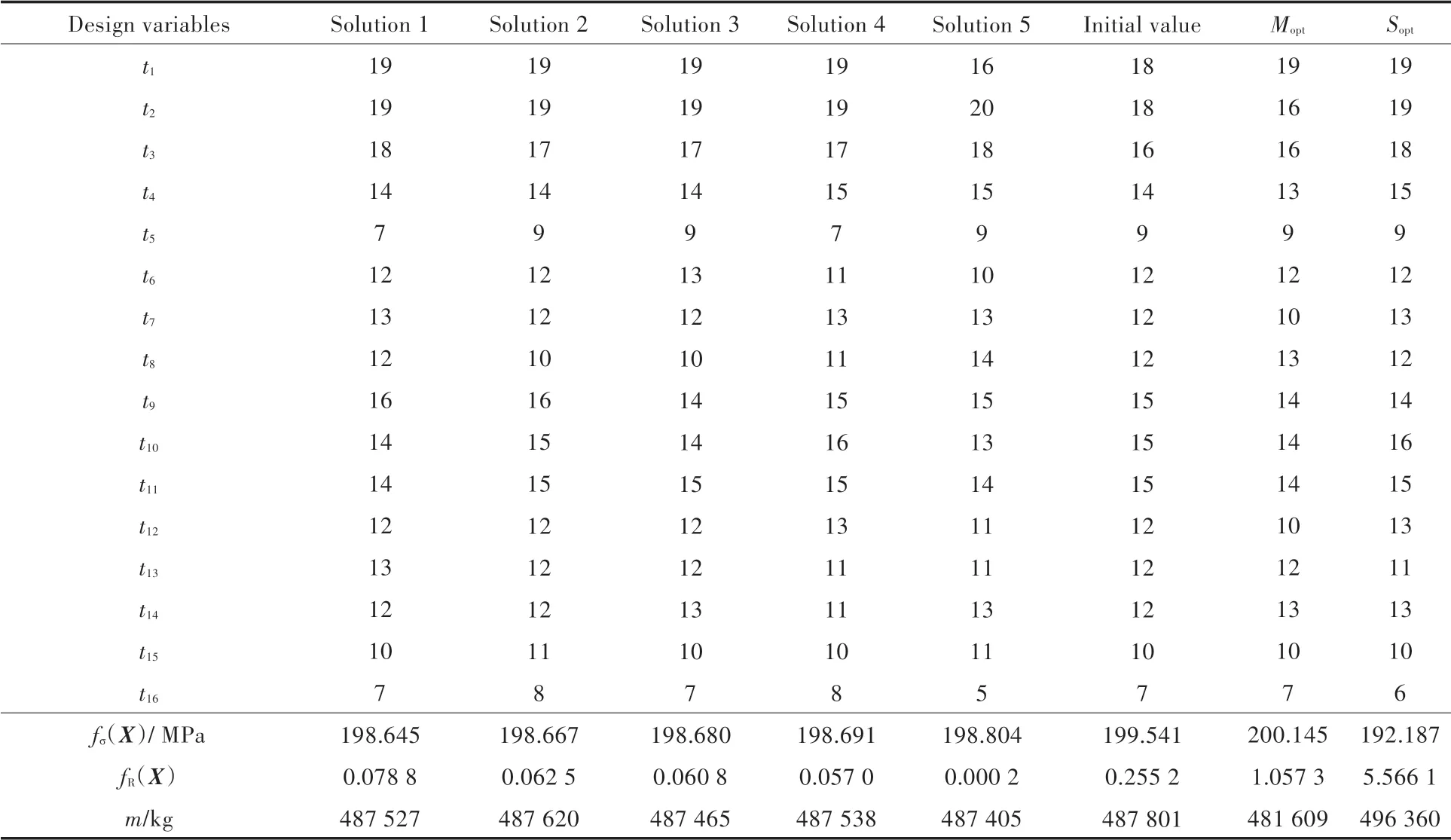
表3 优化结果Tab.3 Optimization results

4 结 论

1）本文将有限元分析与鲁棒性思想相结合，以有限元分析得出的结构响应值为基础，采用支持向量机的方法建立了高精度的近似模型。利用近似模型，得出鲁棒性优化中的目标函数值或约束特性值。同时，通过采用蒙特卡罗积分模拟鲁棒性指标函数，采用编写的粒子群多目标优化算法完成对船舶中横剖面的鲁棒性优化，得到了满意的鲁棒解，说明此方法可行。

2）常规优化解多处于可行域的边界上，或者不具有足够的鲁棒性，设计变量发生微小的波动，目标函数即会发生变化，其优化解有可能不在可行域中，而变为非可行解。因此，传统的优化中需要考虑设计方案的鲁棒性问题。

［1］周继胜，张圣坤.基于可靠性的船体舯剖面鲁棒设计方法［J］.中国造船，2000，41（2）：28-33.ZHOU Jisheng，ZHANG Shengkun. Reliability-based ship midsection structure robust design［J］. Shipbuild⁃ing of China，2000，41（2）：28-33.

［2］于利磊，唐文勇，张圣坤，等. 基于理想点法的双目标结构鲁棒设计［J］. 上海交通大学学报，2003，37（8）：1193-1197.YU Lilei，TANG Wenyong，ZHANG Shengkun. et al.Bi-objective structural robust design using ideal point approach［J］. Journal of Shanghai Jiaotong University，2003，37（8）：1193-1197.

［3］于利磊，唐文勇，张圣坤，等.一种工程结构的鲁棒优化设计方法［J］. 上海交通大学学报，2003，37（8）：1189-1192.YU Lilei，TANG Wenyong，ZHANG Shengkun，et al.Robust optimization design method for engineering structures［J］. Journal of Shanghai Jiaotong University,2003，37（8）：1189-1192.

［4］程远胜，曾广武.鲁棒设计方法及其在造船工程中的应用——第十二届全国结构工程学术会议特邀报告［J］.工程力学，2003（增刊）：1-6.

［5］程远胜，钟玉湘，游建军，等.基于凸集模型的船舶坐墩配墩鲁棒设计方法［J］. 中国造船，2004，45（1）：72-78.CHENG Yuansheng，ZHONG Yuxiang，YOU Jianjun，et al. Robust design of docking blocks using convex models［J］. Shipbuilding of China，2004，45（1）：72-78.

［6］程远胜，钟玉湘，游建军. 概率及非概率不确定性条件下结构鲁棒设计方法［J］.工程力学，2005，22（4）：10-14，42.CHENG Yuansheng，ZHONG Yuxiang，YOU Jianjun.Structural robust design subject to probabilistic and non-probabilistic uncertainties［J］. Engineering Me⁃chanics，2005，22（4）：10-14，42.

［7］骆伟，唐文勇，张圣坤，等.34 万吨级FPSO 的中横剖面鲁棒设计［J］.船舶力学，2005，9（2）：65-71.LUO Wei，TANG Wenyong，ZHANG Shengkun，et al.Robust design of the transverse section of the 340 000 DWT FPSO's midship［J］. Journal of Ship Mechanics，2005，9（2）：65-71.

［8］DIEZ C，PERI D. Robust optimization for ship concep⁃tual design［J］. Ocean Engineering，2010，37（11/12）：966-977.

［9］李亚林，陈静，罗彪，等. 一种求解鲁棒优化问题的多目标进化方法［J］. 计算机工程与应用，2011，47（24）：58-61，76.LI Yalin，CHEN Jing，LUO Biao，et al. Evolutionary multi-objective approach for solving robust optimiza⁃tion problem［J］. Computer Engineering and Applica⁃tions，2011，47（24）：58-61，76.

［10］KAVEH A，TALATAHARI S. A particle swarm ant colony optimization for truss structures with dis⁃crete variables［J］. Journal of Constructional Steel Re⁃search，2009，65（8/9）：1558-1568.

［11］VAPNIK V.Statistical learning theory［M］.New York：Wiley NY，1998.

［12］CORINNA C，VLADIMIR V.Support-vector networks［J］.Machine Learning，1995，20（3）：273-297.