基于CFD的双艉船型阻力数值预报
方昭昭,赵丙乾,陈庆任
1 中国舰船研究设计中心,湖北武汉430064
2 中国船级社武汉规范研究所,湖北武汉430022
0 引 言
国际海事组织(IMO)于2011年7月通过了MARPOL 附则VI 有关船舶能效规则的修正案,确立了船舶能效指数(EEDI)及船舶效能管理计划(SEEMP)等新要求,并将其分阶段强制实施[1-2]。EEDI 等新要求的实施,必将促进海事界向节能减排及绿色环保方向发展[3-4]。双艉船型作为一种优秀的节能船型,在当今世界范围内取得了良好的经济效益,特别是在我国内河和沿海流域,以优良的快速性和操纵性在内河和江海直达运输船型中独占鳌头,应用颇为广泛。
按照MARPOL 附则和船舶能效设计验证指南对EEDI 检验的要求,在设计阶段,船东或造船厂应提供船舶满载或试航状态下的功率—航速估算曲线[5]。因此,要准确计算船舶设计能效就必须准确预报功率—航速曲线,而其中的关键就是阻力的准确预报[6]。
近年来,随着计算技术的飞速发展和计算数学理论的不断完善,计算流体动力学(CFD)得到了蓬勃发展,成为了船舶水动力学性能分析的重要手段之一。基于CFD 的数值预报因具有费用低、无触点流场测量、无尺度效应、能消除物理模型试验中由传感器尺寸及模型变形等因素对流场的影响、可获得较为详细的流场信息等优点而广受关注,在船舶阻力性能预报方面的应用也越来越广泛[7-14]。由于双艉船型艏艉线型复杂,船体表面曲率变化大,流场的数值模拟,尤其是艉部模型的生成及数值处理较困难,因此迄今为止,有关该船型基于CFD 的阻力预报研究较少[15]。
本文将基于计算流体动力学理论,提出一种双艉船型的阻力数值预报方法,即采用SHIP⁃FLOW 软件,基于势流理论计算兴波阻力,并基于粘性流理论计算粘性阻力。通过对某典型的散货双艉船与液货双艉船在不同航速下的阻力开展数值预报,并将数值结果与试验数据[16]作比较,以验证所提方法的正确性。
1 计算原理
1.1 计算区域划分
运用SHIPFLOW 软件进行阻力预报时,不同的阻力成分对应的理论模型和计算原理各不相同。如图1 所示,该软件将计算流场划分为了3 个区域:势流区、边界层区、粘性流区。

图1 SHIPFLOW 中计算流场区域的划分Fig.1 Divisions of the zones in SHIPFLOW
势流区域(Zone I):采用势流面元法计算模块计算兴波阻力及波形。
边界层区域(Zone II):求解边界层方程模块,可计算船体的摩擦阻力。
尾部粘性流区域(Zone III):求解RANS 方程的粘性流场计算模块。该模块由势流区域提供流场边界条件(如入流边界),计算摩擦阻力和粘压阻力等。
1.2 基于势流方法的兴波阻力计算
假定船舶以匀速V 在静水中直线航行,采用大地固定坐标系o-xyz。其中xoy 平面在静水面上,x 轴正方向与船舶航向一致,y 轴正方向指向右舷,z 轴竖直向下,如图2 所示。

图2 坐标系Fig.2 The coordinate system
假定流场中的流体为无粘、无旋、不可压的理想流体,则存在一定常速度势ϕ,它满足控制方程:

速度势ϕ 满足自由面边界条件、物面边界条件以及远方辐射条件:

式中:Vs=(V,0,0);g 为重力加速度;R 为流场中某点离扰动源的距离;n 为物面法向矢量。
上述式(1)~式(4)就构成了流体速度势的定解问题,可采用势流Rankine 源法求解。即在船体表面和自由面布置源(汇),则流场中任意点P(x,y,z)的速度势表达为

式中:P(x,y,z) 为场点;Q(x0,y0,z0) 和Q′(x0,-y0,z0)为源(汇)点;σ(Q)为源强分布;r和r′为场点与源(汇)点之间的距离。
将流体速度势表达式(5)代入式(2)及式(4),求解源点源强分布σ(Q)。再由式(5)可得到流体域任意场点的流体速度势ϕ(P),由式(2)可得到船体兴波波形。
一旦求解出流体速度势ϕ,根据伯努利方程,便可得到流场中的压力(单位:Pa)分布:

式中,ρ 为流体质量密度。
将流体压力沿船体湿表面进行积分,得到船体所受到的流体作用力与力矩:

式中:r 为原点至船体表面点P(x,y,z)的矢径;n=(n1,n2,n3),为点P(x,y,z)处的单位法向矢量。
船体兴波阻力为

无因次的兴波阻力系数

式中,S0为船体湿表面积。
1.3 基于RANS 方程的粘性阻力计算
当船舶以航速V 在水中匀速航行时,船体受到的流体粘性阻力可通过模拟船体粘性叠模绕流场得到,控制方程为RANS 方程:
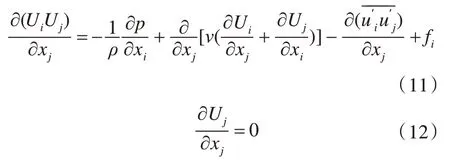
式中:Ui为流体质点在i方向的速度分量;ν为运动粘性系数;fi为体积力在i 方向的分量;为雷诺应力项。
上述控制方程并不封闭,需添加描述流体湍动特征的湍流模型方程。这里采用标准的k-ε模型湍流输运方程,湍动能k 方程和湍动耗散率ε 方程分别为:

式中:Gk表示由平均速度梯度产生的湍流动能;Gb为由浮力产生的湍流动能;c1ε,c2ε和c3ε为经验常数;σk和σε分别为k 和ε 对应的Prandtl 数;Sk和Sε为源项;μ 为流体的动力粘性系数;uτ为湍流粘性系数。
对式(11)~式(14)采用有限差分法进行数值求解,可计算得到船体粘性绕流场的压力与速度分布。其中:船体表面的压力沿船体湿表面的积分为船体受到的粘性流体总压力,该力沿着与船舶航速方向相反的分量为粘压阻力;船体表面的速度梯度乘以流体粘性系数为船体表面的流体切应力,将其沿船体湿表面进行积分则得到船体受到的流体总摩擦力,该力沿着与船舶航速方向相反的分量即为船体摩擦阻力。
2 算例描述
本文以某散货双艉船与液货双艉船为例,分别对其船模阻力进行数值预报。液货双艉船的横剖面型线图如图3 所示,从中可看出,这种船型艏艉部的曲面曲率变化非常复杂。

图3 某液货双艉船横剖面型线图Fig.3 The plans of the liquid cargo ship with twin-skeg
散货双艉船船模的缩尺比为15.83,其主要参数如表1 所示,船模的计算航速如表2 所示。液货双艉船船模的缩尺比为16.0,其主要参数如表3所示,船模的计算航速如表4 所示。

表1 散货双艉船的主要参数Tab.1 Principal dimensions of the bulk cargo ship with twin-skeg

表2 散货双艉船船模的计算航速Tab.2 The speeds of the bulk cargo ship model with twin-skeg

表3 液货双艉船的主要参数Tab.3 Principal dimensions of the liquid cargo ship with twin-skeg

表4 液货双艉船船模的计算航速Tab.4 The speeds of the liquidcargo ship model with twin-skeg
3 数值计算
3.1 计算模型
SHIPFLOW 根据加密的分站型线建立船体表面模型。如通过Catia 和Rhino 等三维建模软件建立船壳表面,然后导入SHIPFLOW 生成计算所需的型值文件。图4 所示为散货双艉船的全船模型;图5 所示为艉部局部模型。

图4 散货双艉船数值模型Fig.4 The configuration of the bulk cargo ship model with twin-skeg

图5 散货双艉船的艉部模型(一半)Fig.5 The half stern sketch of the bulk cargo ship with twin-skeg
3.2 网格划分
SHIPFLOW 软件中,是用势流方法计算兴波阻力,面元的分布影响结果精度;采用粘性流方法计算粘性阻力,体网格的划分对结果精度有一定的影响。为了提高计算精度,结合船型自身特征及航行的特点,兴波阻力计算的面网格划分应注意以下几点:
1)在船体瞬时湿表面、瞬时自由面均需划分面元网格,并分布速度源或汇。
2)在船体表面上,对于曲率变化较大的艏、艉区域,面元网格应进行加密。
3)在自由面上,面元网格沿船长方向的分布应尽量均匀,沿宽度方向船体附近的网格应较密。
4)艉封板后的自由面需划分面元网格。
5)不同航速下,面元网格的数量不同。一般较低航速(Fn<0.2)的面元网格数量比较高航速(Fn>0.2)的大。
对于粘性阻力计算的体网格划分,应注意以下几点:
1)只在船体中、后部划分体网格,网格类型为整体结构化贴体网格。
2)在船体表面进行贴体网格的加密,第1 层网格厚度对应的y+值约取为1~2。
3)粘压阻力的计算精度与艉封板周围的网格质量关系较大,因此在生成真实、精确的艉封板形状的基础上,其周围应划分加密的贴体结构化网格。
兴波阻力计算中面网格的划分如图6 所示,粘性流场计算中体网格的划分如图7 所示。
3.3 阻力的数值预报结果
3.3.1 散货双艉船的阻力计算结果
1)兴波阻力计算结果。
表5 给出了散货双艉船船模在不同航速下兴波阻力系数的计算结果,其中Cw为兴波阻力系数。

图6 兴波阻力计算中面网格的划分Fig.6 The mesh for calculating wave-making resistance in potential flow

图7 粘性流场计算中尾部体网格的划分Fig.7 The stern mesh for calculating viscosity resistance in viscous flow

表5 散货双艉船船模的兴波阻力系数计算结果Tab.5 The coefficients of wave-making resistance for the bulk cargo ship model with twin-skeg

图8 散货双艉船船模的兴波阻力系数变化曲线Fig.8 Coefficients curve of the wave-making resistance for the bulk cargo ship model with twin-skeg
图8 给出了兴波阻力系数随航速的变化曲线。从中可以看出,在该航速段内,兴波阻力系数随着航速的增加而增大。在Fn=0.19 附近,兴波阻力系数快速增加。图9 给出了该船模在3 个不同航速下的兴波波形等高线图。从中可以看出,数值计算能较好地反映出船体兴波的船艏波系和艉波系,其散波和横波特征均能得到较好的描述。

图9 不同航速下散货双艉船船模船体兴波波形Fig.9 Wave contours for the bulk cargo ship model with twin-skeg advancing at different speeds
2)剩余阻力计算结果。
表6 给出了散货双艉船船模在不同航速下的剩余阻力计算结果,图10 给出了剩余阻力系数计算结果与试验数据随航速的变化曲线。

表6 散货双艉船船模的剩余阻力系数计算结果Tab.6 The coefficients of residual resistance for the bulk cargo ship model with twin-skeg

图10 散货双艉船船模的剩余阻力系数变化曲线Fig.10 Coefficients curves of residual resistance for the bulk cargo ship model with twin-skeg
3)摩擦阻力计算结果。
表7 给出了散货双艉船船模在不同航速下的摩擦阻力计算结果,并与1957 ITTC 公式估算结果进行了比较。从中可以看出,摩擦阻力系数的数值计算结果和1957 ITTC 公式的估算结果相比略小。其主要原因是:由于双艉船型长宽比较小,船体表面纵向曲率大,艉部形状复杂,一方面,船体表面边界层流动情况与平板边界层流动情况不同,在船体曲骤处,特别是较丰满船的艉部易发生边界层分离,产生漩涡,摩擦阻力下降;另一方面,双艉船型艉部较肥大,去流段短,粘压阻力较单艉船型大,剩余阻力系数和二因次换算试验结果相比也大。
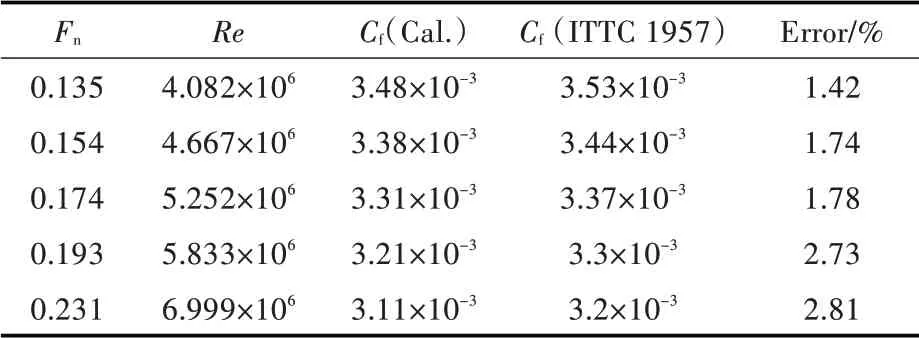
表7 散货双艉船船模的摩擦阻力系数计算结果Tab.7 The coefficients of frictional resistance for the bulk cargo ship model with twin-skeg
4)总阻力计算结果。
表8 给出了散货双艉船船模的总阻力计算结果,图11 给出了总阻力系数变化曲线。这里的总阻力为兴波阻力与粘性阻力之和,也即摩擦阻力与剩余阻力之和。由表8 与图11 均可看出,总阻力的数值计算结果与试验数据非常接近,总阻力系数曲线的趋势也一致,最大误差不超过2%,表明本文的数值计算方法具有较高的精度。

表8 散货双艉船船模的总阻力系数计算结果Tab.8 The coefficients of total resistance for the bulk cargo ship model with twin-skeg

图11 散货双艉船船模的总阻力系数变化曲线Fig.11 Coefficients curves of total resistance for the bulk cargo ship model with twin-skeg
3.3.2 液货双艉船的阻力计算结果
1)兴波阻力计算结果。
表9 给出了液货双艉船船模在不同航速下兴波阻力系数的计算结果,图12 给出了兴波阻力系数随航速的变化曲线。从中可以看出,在该航速段内,兴波阻力系数随着航速的增加而增大,在Fn=0.184 附近,兴波阻力系数快速增加。图13 给出了该船模在3 个不同航速下的兴波波形等高线图。可以看出,数值计算能较好地反映出船体兴波的船艏波系和艉波系,其散波和横波特征均能较好地得到描述。

表9 液货双艉船船模的兴波阻力系数计算结果Tab.9 The coefficients of wave-making resistance for the liquid cargo ship model with twin-skeg

图12 液货双艉船船模的兴波阻力系数变化曲线Fig.12 Coefficients curve of the wave-making resistance for the liquid cargo ship model with twin-skeg

图13 不同航速下液货双艉船船模船体兴波波形Fig.13 Wave contours for the liquid cargo ship model advancing at different speeds with twin-skeg
2)剩余阻力计算结果。
表10 给出了液货双艉船船模在不同航速下剩余阻力系数的计算结果,图14 给出了剩余阻力系数计算结果与试验数据随航速的变化曲线。
3)摩擦阻力计算结果。
表11 给出了液货船船模在不同航速下摩擦阻力系数的计算结果及其与1957 ITTC 公式估算结果的比较。

表10 液货双艉船船模的剩余阻力系数计算结果Tab.10 The coefficients of residual resistance for the liquid cargo ship model with twin-skeg

图14 液货双艉船船模的剩余阻力系数变化曲线Fig.14 Coefficients curves of residual resistance for the liquid cargo ship model with twin-skeg

表11 液货双艉船船模的摩擦阻力系数计算结果Tab.11 The coefficients of frictional resistance for the liquid cargo ship model with twin-skeg
4)总阻力计算结果。
表12 给出了液货双艉船船模的总阻力系数计算结果,图15 给出了总阻力系数的变化曲线。从表12 与图15 均可看出,总阻力系数的数值计算结果与试验数据非常接近,总阻力系数曲线的趋势也一致,最大误差为3.66%,表明文中数值计算方法具有较高的精度。

表12 液货双艉船船模的总阻力系数计算结果Tab.12 The coefficients of total resistance for the liquid cargo ship model with twin-skeg

图15 液货双艉船船模的总阻力系数变化曲线Fig.15 Coefficients curves of total resistance for the liquid cargo ship model with twin-skeg
3.3.3 结果分析
分别比较两种不同类型双艉船船模的总阻力数值结果与试验数据,可以看出:这两种船型的总阻力计算结果与试验数据吻合较好,各航速下的总阻力计算误差均在4%以内,且总阻力随航速的变化趋势与试验结果也较一致。
就计算结果与船模阻力试验二因次换算结果来看,两种船型的摩擦阻力系数数值计算结果均比基于平板边界层理论的ITTC 1957 估算公式的值略小,同时剩余阻力系数的数值计算结果比试验的二因次换算的结果大。其主要原因是:由于双艉船型长宽比较小,船体表面纵向曲率大,艉部形状复杂,一方面,船体表面边界层流动情况与平板边界层流动情况不同,特别是双艉型船艉部较丰满,易发生边界层分离;另一方面,双艉型船艉部较肥大,去流段短,粘压阻力较单艉船型大,因此计算的剩余阻力系数比二因次换算试验的结果要大。
比较散货船船模与液货船船模的阻力数值计算结果,发现这两种船型的主尺度几乎相同,且形状相似,但液货船的方形系数较散货船的大,因此液货船的水线面系数较大。在相同傅汝德数情况下,液货船的兴波阻力比散货船的大,例如,当Fn=0.175 时,液货船船模的兴波阻力系数为1.286×10-3,粘性阻力系数为3.914×10-3;当Fn=0.174时,散货船船模的兴波阻力系数为0.758×10-3,粘性阻力系数为3.822×10-3,粘性阻力系数非常相近。
4 结 语
本文给出了一种基于CFD 理论进行双艉船型阻力数值预报的方法。采用非线性势流方法计算船体兴波阻力,基于粘性流方法计算船体粘性阻力。分别对典型散货双艉船与液货双艉船在不同航速下的阻力进行了数值预报,并将数值计算结果与试验数据进行了比较。结果显示,总阻力误差均在4%以内,且阻力的数值计算结果随航速的变化趋势与试验结果吻合良好。研究表明,该方法计算效率较高、易于实现、经济性较好且预报精度能满足工程需要,具有较强的工程实用性。
[1]国际海事组织. 防污公约2011 综合文本[M]. 北京:人民交通出版社,2012.
[2]李路,芮晓松.论EEDI(能效设计指数)的强制实施的合理性[J].中国造船,2011,52(增刊1):33-37.LI Lu,RUI Xiaosong. Comments to the compulsory im⁃plementation of EEDI [J]. Shipbuilding of China,2011,52(Supp1):33-37.
[3]周伟新,李百齐,胡琼,等. 中国船舶科学研究中心关于EEDI 的研究进展[J].中国造船,2011,52(4):13-22.ZHOU Weixin,LI Baiqi,HU Qiong,et al. EEDI—An important factor of green ship studied in China Ship Scientific Research Center[J]. Shipbuilding of China,2011,52(4):13-22.
[4]刘飞,林焰,李纳,等.我国船舶EEDI 分析研究[J].中国造船,2012,53(4):128-136.LIU Fei,LIN Yan,LI Na,et al. Research on EEDI analysis for the ships of China[J]. Shipbuilding of Chi⁃na,2012,53(4):128-136.
[5]中国船级社. 绿色船舶规范[M]. 北京:人民交通出版社,2012.
[6]盛振邦,刘应中.船舶原理(上册)[M].上海:上海交通大学出版社,2003.
[7]HUA Z L,XING L H,GU L. Application of modified quick scheme to depth-averaged k-epsilon turbulence model based on unstructured grids[J]. Chinese Journal of Hydrodynamics(Ser.B),2008,20(4):514-523.
[8]KIM K J. Ship flow calculation and resistance minimi⁃zation[D]. Gothenburg,Sweden:Chalmers University of Technology,1989.
[9]吴晓莲. 基于CFD 的船舶球艏/球艉低阻线型研究[D].哈尔滨:哈尔滨工程大学,2008.
[10]陈伟,许辉,邱辽原,等. 基于SHIPFLOW 软件的方尾舰船阻力快速预报[J]. 中国舰船研究,2012,7(4):17-22.CHEN Wei,XU Hui,QIU Liaoyuan,et al. Fast re⁃sistance prediction for ship with transom stern based on SHIPFLOW[J]. Chinese Journal of Ship Re⁃search,2012,7(4):17-22.
[11]徐力,陈作钢.船体艏部水动力性能优化[J].中国舰船研究,2012,7(2):37-64.XU Li,CHEN Zuogang. Hydrodynamic performance optimization of ship hull's forebody[J]. Chinese Jour⁃nal of Ship Research,2012,7(2):37-64.
[12]倪崇本,朱仁传,缪国平,等. 一种基于CFD 的船舶总阻力预报方法[J]. 水动力学研究与进展(A辑),2010,25(5):579-586.NI Chongben,ZHU Renchuan,MIAO Guoping,et al. A method for ship resistance prediction based on CFD computation[J]. Chinese Journal of Hydrody⁃namics(Ser.A),2010,25(5):579-586.
[13]NI S Y. Higher order panel method for potential flows with linear or non-linear free surface boundary condi⁃tions[D]. Gothenburg,Sweden:Chalmers Universi⁃ty of Technology,1987.
[14]方昭昭,朱仁传,缪国平,等. 基于数值波浪水池的波浪中船舶水动力计算[J]. 水动力学研究与进展(A 辑),2012,27(5):515-524.FANG Zhaozhao,ZHU Renchuan,MIAO Guoping,et al. Numerical calculation of hydrodynamic forces for a ship in regular waves based on numerical wave tank[J]. Chinese Journal of Hydrodynamics(Ser. A),2012,27(5):515-524.
[15]张净宙.双尾(鳍)船型线特征及局部变形设计方法研究[D].武汉:武汉理工大学,2007.
[16]张伟.内河典型船型船机桨匹配优化及推进效率研究报告[R]. 武汉:中国船级社武汉规范研究所,2012.

