小型LNG船C型独立液舱内部压力计算
关心,马坤,管官
1 大连理工大学 船舶CAD 工程中心,辽宁 大连116024
2 大连理工大学船舶工程学院工业装备结构分析国家重点实验室,辽宁 大连116024
0 引 言
液化天然气(LNG)作为一种高效清洁的能源,在世界范围内越来越受到人们的重视[1]。近年来,沿海、沿江的LNG 接收站不断兴起,在LNG 产业链中,从大型LNG 接收站到小型LNG 接收站的二程转运任务,都需要由小型LNG 船来完成[2]。独立C 型液舱可以承受较高的货物压力,是一种压力容器,被称为最安全的LNG 液舱。其设计相对简单,不需要复杂的次屏壁,维护费用低,技术相对成熟[3]。在短途运输中,可以不用处理蒸发气(Boil Off Gas,BOG),大大减少了设备成本。
对于C 型独立液舱的结构尺寸,应该根据液舱的内部压力,按照通用压力容器的设计原理进行计算[4],然后再加载其他载荷进行分析和校核。内部压力计算是小型LNG 船C 型独立液舱设计中最基本、也是最重要的部分,初步确定的板厚准确与否,直接关系到后续校核工作量的大小和整个独立液舱的重量,影响船舶的技术经济性。
小型LNG 船内部液体的压力受船舶航行过程中的纵荡、横荡、垂荡、横摇、纵摇和艏摇的影响。在传统的计算方法中,是分别在x-z 和y-z 平面计算并取较大值作为最终的内部液体压力值,同时用于板厚计算,但这种简化方法并未完全模拟出实际的压力情况。
本文将提出一种同时考虑三向加速度的内部压力计算方法,以应用于板厚的三维计算,并以某单圆筒球形封头独立液舱为例比较二维方法与三维方法计算结果的差异。同时,分析静力和动力加速度联合作用对板厚的影响。
1 计算原理及程序设计
1.1 加速度分量的计算
由船舶运动而产生的3 个方向的加速度可以在液舱重心处予以估算,根据IMO《国际散装运输液化气体船舶构造与设备规则》[5]提出的加速度分量的指导公式进行计算。
1)垂荡、纵摇及横摇的垂向运动加速度az:
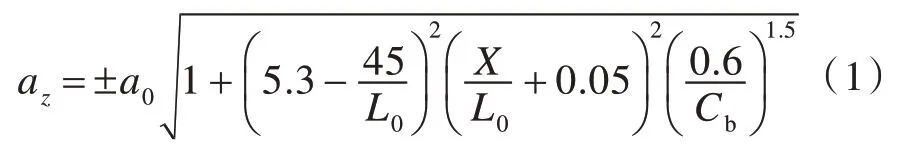
2)横荡、艏摇和横摇的横向运动加速度,以及由横摇的重力分量组成的横向加速度ay:
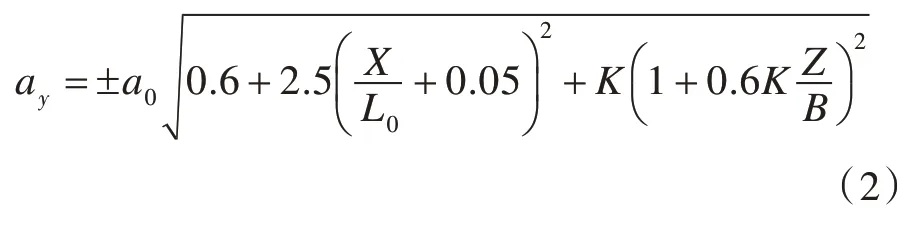
3)纵荡和纵摇的纵向运动加速度,以及由纵摇的重力分量组成的纵向加速度ax:

其中:
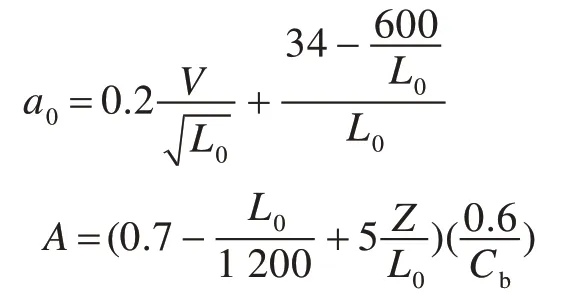
以上式中:L0为船长,m;B 为船舶最大型宽,m;Cb为方形系数;X 为船舯至液罐重心的纵向距离(其在船舯前面为正,船舯后面为负),m;Z 为从船的实际水线至液罐重心的垂向距离(其在水线上为正,水线下为负),m;K 为系数,通常取K=1;V 为营运航速,kn。
ax,ay和az为相应方向上的最大无因次加速度(相对于重力加速度)。计算时,可以认为它们是分别作用的,其中az不包括静重力分量。
以上公式是作为计算由船舶在北大西洋中以相当于概率水平为10-8的运动而产生的加速度分量的指导公式,且适用于船长超过50 m 的船舶。
1.2 内部压力计算
内部压力Peq(单位MPa)是由设计蒸气压力Po(单位MPa)和内部液体压力Pgd合成的结果,但不包括液体晃动的影响,按下式计算:

内部液体压力Pgd(单位MPa)是考虑船舶运动的长期分布,包括船舶在其使用寿命期间在不规则海浪中所经受的纵荡、横荡、垂荡、横摇、纵摇和艏摇的影响,以及所引起的动力加速度和货物重力加速度联合作用所产生的压力,按下式计算:
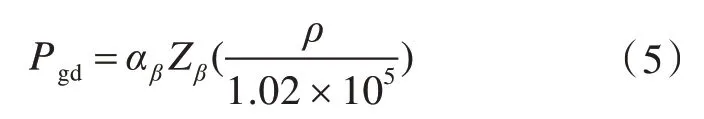
式中:αβ为在任意的β 方向上由重力和动载荷引起的无因次加速度(相对于重力加速度);ρ 为设计温度时的货物最大密度,kg/m3;Zβ为从所决定的压力点沿β 方向向上量至液舱壳板的最大液柱高度,m。
从上面的公式中可以看出,需要考虑两个变量,即合成加速度αβ和压力点上沿β 方向的最大液柱高度。内部液体压力是针对特定的压力点而言的,即液舱内壁的不同压力点对应不同的压力。需求得各个压力点上可能出现的最大压力,以计算对应的最小板厚。
求内部液体压力的最大值,即需要求得合成加速度αβ与方向β 上最大液柱高度的乘积的最大值。由于这两个变量一般不同时达到最大,因此需要计算出所有可能的情况,对其乘积进行比较,以得到需要的结果。由于工作量巨大,这一部分通常由计算机程序来完成。
1.2.1 合成加速度αβ的计算
合成加速度αβ是由上文所述的3 个无因次加速度分量ax,ay,az和重力加速度合成而得到的。三向加速度的合成有2 种方法:
1)传统的二维计算方法。
为简化计算过程,可以在ax和az组成的x-z 平面求出αβ(x-z),在ay和az组成的y-z平面求出αβ(y-z),即通过加速度椭圆方程进行计算。y-z 平面的加速度椭圆如图1 所示。
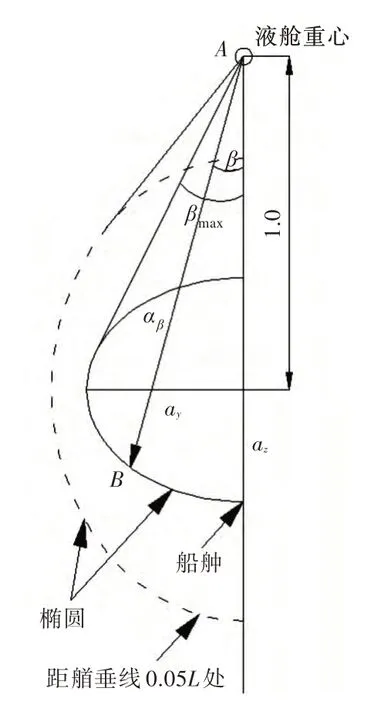
图1 y-z平面的加速度椭圆Fig.1 Acceleration ellipse in y-z plane
椭圆的两个轴的长度分别为2ay和2az,液舱重心距离椭圆中心为一个无因次的重力加速度。将合成加速度αβ(y-z)的倾角记为β1,合成加速度αβ(x-z)的倾角记为β2。合成加速度的大小可以表示为起点在液舱重心、终点在加速度椭圆上的直线段的长度,即直线段AB。A 点固定不动,B 点在椭圆上运动,其长度可以通过倾角β1来表示。
为计算内部液体压力,还需要分别在横向和纵向平面计算最大液柱高度。由于压力容器的几何形状比较规则,所以通过简单的几何分析就可以得到计算公式。
通过这种平面计算方法,在同一个压力点可以得出横向和纵向两个最大内部液体压力,取较大值即可完成近似计算。很显然,虽然该计算过程简单,但通过这种方法得到的计算结果却并不精确。
2)三维计算方法。
由于合成加速度的所有取值实际在一个椭球上,所以可以采用直接计算的方法,利用加速度椭球方程进行计算,即三维计算方法。可以将三维计算方法分解为若干个二维问题来求解,步骤如下。
设椭球3 个轴的长度为3 个无因次加速度分量ax,ay和az,液舱重心在椭球z 轴的正半轴上,与原点的距离为1。
(1)在-az与az之间任取一个z 值,作垂直于z轴的平面,截得椭圆面xy 如图2 所示。
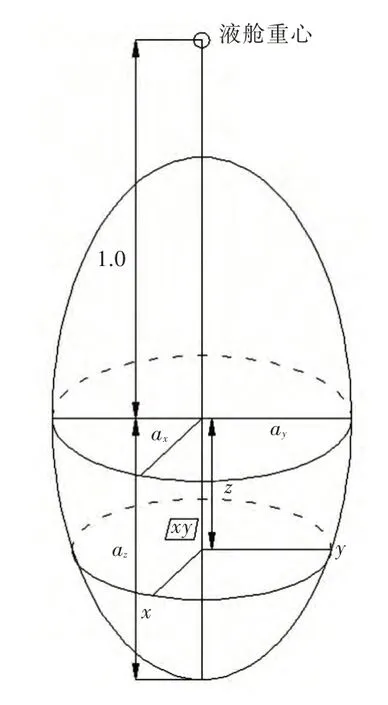
图2 椭球截面Fig.2 Cross section of acceleration ellipsoid
(2)在椭圆轮廓的圆周上任取一点,作为合成加速度线段的端点。
(3)将得到的交点分别投影到x 轴和y 轴,得到ax(z)及ay(z)。
(4)在x-z 平面中,由ax(z)和1+z 的绝对值计算得到对应的倾角β1;在y-z 平面中,采用相同的方法求得β2。此两个倾角用于计算压力点的最大液柱高度。
(5)利 用ax(z),ay(z)和1+z,在三维空间中计算出合成加速度αβ(图3):
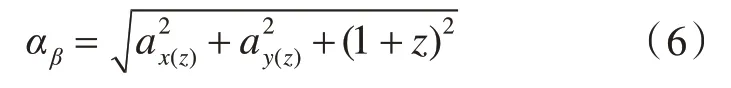
1.2.2 压力点最大液柱高度Zβ的计算
简化的平面计算法的压力点最大液柱高度计算可以通过几何分析法求得。而在三维空间中,倾斜后的最高点不易确定,更难以利用几何方法归纳公式求得。因此,可以借助具有相应查询计算功能的三维建模软件来确定最高点至压力点的高度差。
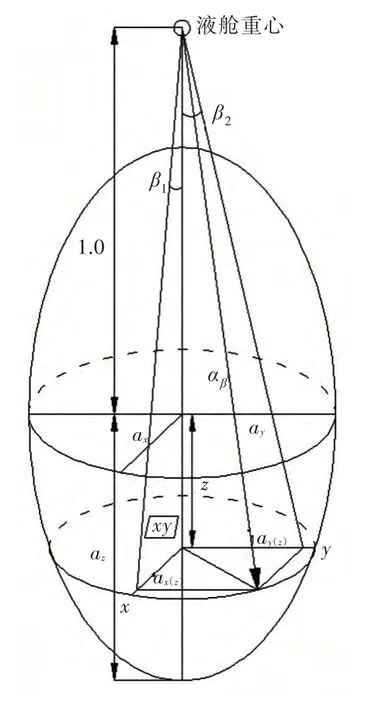
图3 三维加速度合成Fig.3 3-dimensional acceleration composition
选用常用且操作简单的AutoCAD 软件,通过VBA 二次开发,进行建模—倾斜—查询,得到指定压力点对应的最大液柱高度。
1)建模:分别建立封头和筒体,并将其合并为一个整体。
2)倾斜:将原点移动至需要计算的压力点上,以使整个模型绕压力点旋转,即首先在y-z 平面旋转倾角β1,然后在x-z平面旋转倾角β2。
3)查询:利用软件自带的命令查询模型最高点的坐标值,即可得到所需结果。
本文开发了计算程序,可以计算任一压力点对应的所有可能的合成加速度αβ与最大液柱高度Zβ的乘积,然后取其最大值,即可计算出该压力点处的最大液体压力。计算流程如图4 所示。
1.3 板厚计算
根据《国际散装运输液化气船船舶构造与设备规则》及压力容器标准GB 150.3-2011[6],板厚的计算公式如下。
筒体:
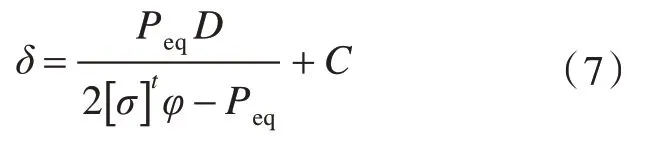
封头:
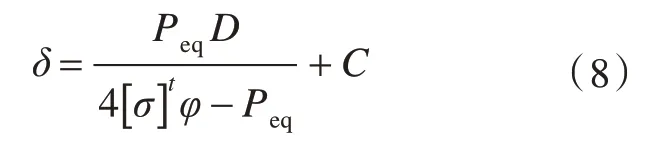
式中:δ 为计算板厚,mm;D 为液罐直径,mm;[σ]t为设计温度下的许用薄膜应力,MPa;φ 为焊接效率系数;C 为腐蚀裕量及板厚公差,mm。
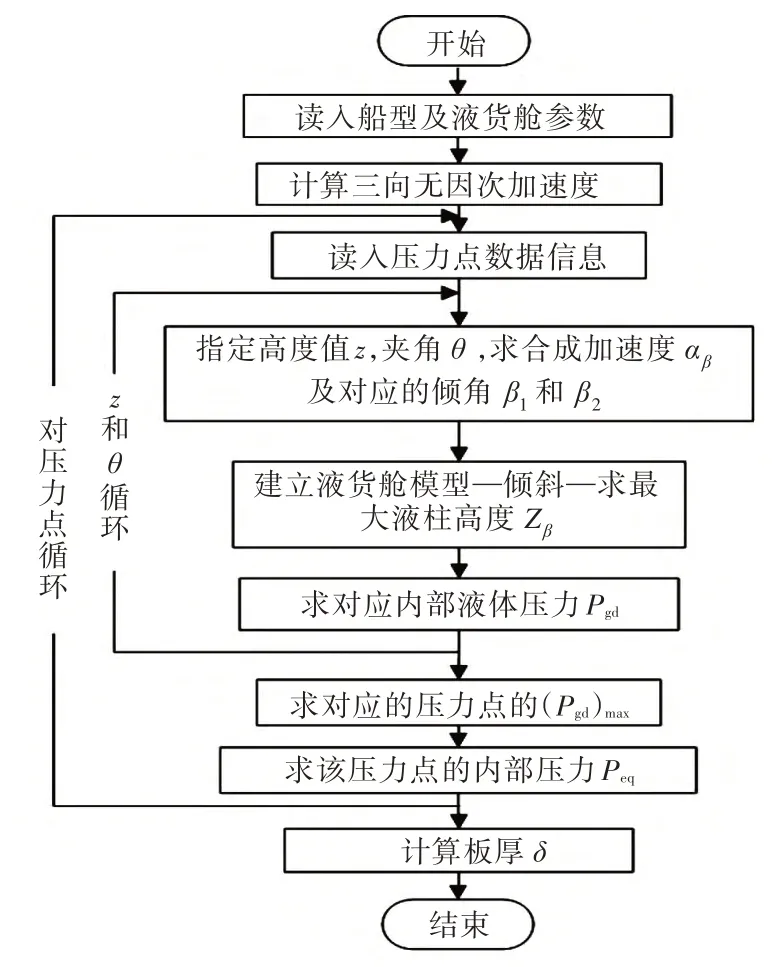
图4 三维法计算流程图Fig.4 Flow chart of the calculation by 3-dimemsional method
2 计算实例
以某多用途小型LNG 船的一个单圆筒C 型液舱的封头和筒体的板厚计算为例:该液舱的设计蒸气压力为0.52 MPa,最大容积4 000 m3,球形封头。结合板材规格及液舱的尺寸,以桔瓣式罐体模型进行布置[7],计算液舱圆筒部分与封头部分交界处的压力点,计算得到的分带角α=40°,即需要计算与圆心连线和z 轴夹角分别为40°,80°,120°,160°及180°的5 个压力点。船型及液舱主要参数如表1 所示。
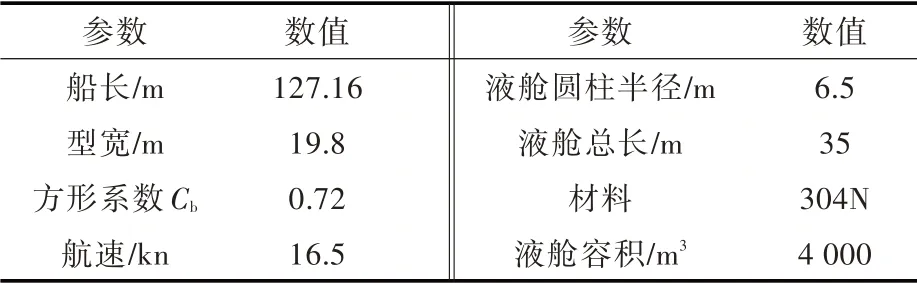
表1 船型及液舱主要参数Tab.1 Main parameters of the ship and its liquid tank
2.1 内部压力及板厚计算结果比较
采用传统的二维方法和文中提出的三维方法编程进行计算,并比较:由货物重力和动力加速度的联合作用所引起的内部液体压力Pgd(图5)、内部压力Peq(图6)以及板厚的计算结果。根据内部压力,可以计算相应5 个压力点处的外壳板最小厚度,其结果如表2 和表3 所示。
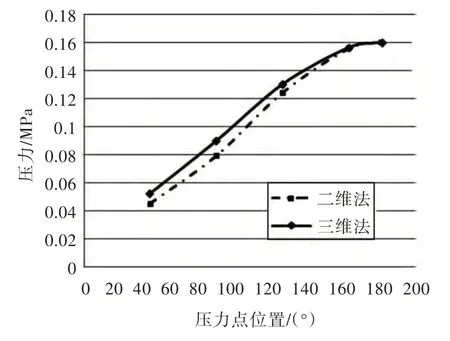
图5 Pgd在二维法及三维法中的计算结果Fig.5 The calculation results of Pgd in 2-dimensional method and 3-dimensional method

图6 Peq在二维法及三维法中的计算结果Fig.6 The calculation results of Peq in 2-dimensional method and 3-dimensional method
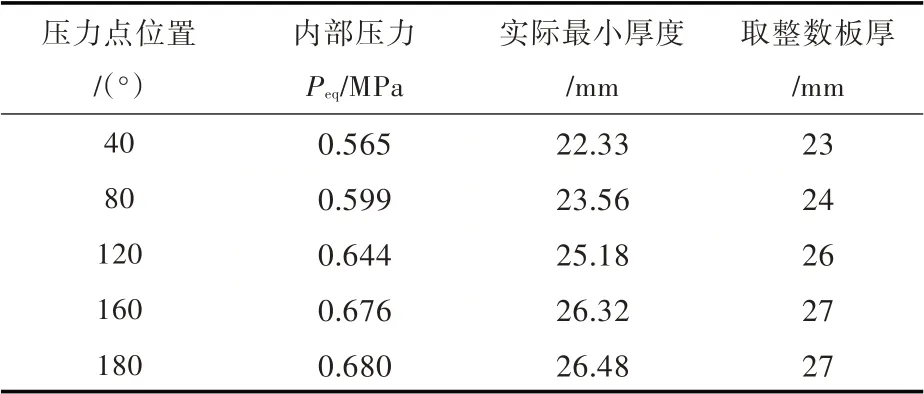
表2 板厚计算结果(二维方法)Tab.2 The calculation results of the plate thickness(2-dimensional method)
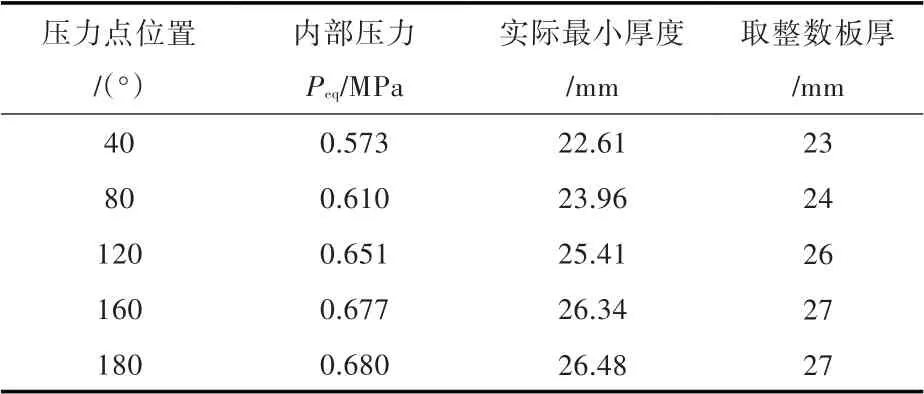
表3 板厚计算结果(三维方法)Tab.3 The calculation results of the plate thickness(3-dimensional method)
通过以上计算结果的比较可以看出,三维法由于同时考虑了三向加速度,其计算结果与仅考虑y-z 或x-z 平面内加速度的二维法相比,计算结果偏大:在单独考虑由货物重力和动力加速度的联合作用所引起的内部液体压力Pgd时,两种方法有较明显的差异;在加入设计蒸气压力Po后,由两种方法计算得到的结果之间的差值占总压力的比例很小,在板厚计算中可以忽略不计。
2.2 加速度联合作用对板厚的影响
以二维法的计算结果为例,对只考虑由货物静重力加速度计算得到的货物压力Ps、考虑由货物重力和动力加速度的联合作用计算得到的内部液体压力Pgd,以及考虑了设计蒸气压力的内部压力Peq进行比较,其结果如图7 所示。
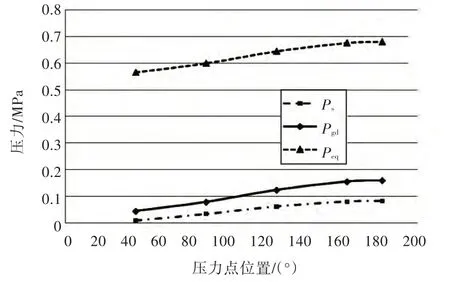
图7 不同压力大小比较Fig.7 Comparison of the values of different pressures
从图中可以看出,与只考虑货物静重力加速度相比,考虑货物重力和动力加速度的联合作用计算所得的压力有明显的增加,说明在设计船舶上使用的C 型独立液舱时,要充分考虑船舶运动带来的影响。
通过板厚的计算来说明影响的大小,结果如表4 和表5 所示。
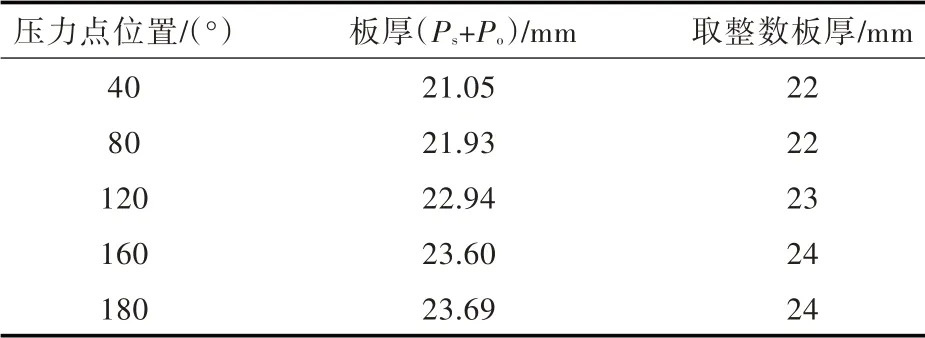
表4 板厚计算结果(Ps+Po)Tab.4 The calculation results of the plate thickness(Ps+Po)
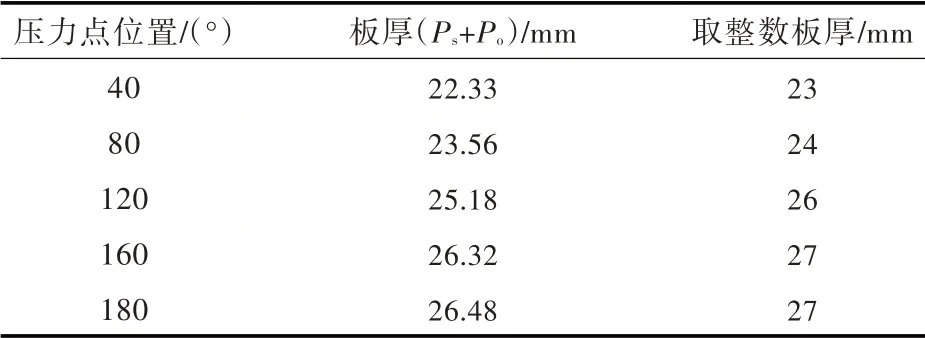
表5 板厚计算结果(Pgd+Po)Tab.5 The calculation results of the plate thickness(Pgd+Po)
表中数据表明,考虑动力加速度后,在不同部位会有1~3 mm 板厚的增加,这说明在算例中的船舶营运环境下,在指定的C 型独立液舱尺寸及设计蒸气压力下,有必要考虑动力加速度对外壳板厚度的影响。
3 结 论
通过对算例计算结果的分析,可以得到如下结论:
1)采用三维计算方法得到的内部液体压力Pgd在不同压力点处较二维法有0%~16%的增大,因此在精确设计时有必要按照三维方法计算。
2)若取设计蒸气压力Po=0.52 MPa,则采用三维计算方法和二维计算方法所得的内部压力Peq的计算结果在差别最大压力点的压力差只占总压力的1.5%,在工程实际中可以忽略不计。
3)由于C 型独立液舱的设计蒸气压力Po通常大于0.3 MPa,因此在对单圆筒球形封头的小型LNG 船液货舱的外壳板厚度进行初步计算时,可采用二维方法代替三维方法。
4)在其他形式液货舱的内部压力计算中,若设计蒸气压力Po较小,例如,对于设计蒸气压力只有0.025 MPa 的薄膜型液舱的内部压力计算,采用三维方法进行计算将更为准确,偏于安全。
上述计算是在特定条件下进行的,其影响因素多样,包括船舶的航速、船长、型宽、方形系数等船舶主尺度及主要参数,以及独立液舱重心距船舯及水线的距离、独立液舱的形状及尺寸、设计蒸气压力的大小等。其中,设计蒸气压力Po与内部液体压力Pgd的比值越大,船舶运动产生的动力加速度对板厚的影响就越小,反之同理。
[1]BUKOWSKI J D. Natural gas liquefaction technology for floating LNG facilities[C]//The 17th International Conference & Exhibition on Liquefied Natural Gas.Texas,USA,2013.
[2]韩文科,杨玉峰. 中国能源展望:观点总结[R]. 北京:国家发展和改革委员会能源研究所,2012.
[3]丁玲,马坤.中小型LNG 运输船液货罐设计技术[J].船舶,2010(1):26-29.DING Ling,MA Kun. Design technology of liquid car⁃go tank in small and medium LNG carrier[J]. Ship and Boat,2010(1):26-29.
[4]TABAKOV P Y,WALKER M. Design optimization of anisotropic pressure vessels with manufacturing uncer⁃tainties accounted for[J]. International Journal of Pres⁃sure Vessels and Piping,2013,104:96-104.
[5]IMO. International code for the construction and equip⁃ment of ships carrying liquefied gases in bulk:ICG code[M].London:IMO,1993.
[6]GB 150.3-2011 压力容器 第3 部分:设计[S]. 北京:中国标准出版社,2012.
[7]汤永贵. 钣金工展开计算手册[M]. 北京:冶金工业出版社,2002.

