文丘里式气泡发生器工作特性分析

居晓峰 孙立成 唐文偲 运红宇 阎昌琪

1（哈尔滨工程大学 核安全与仿真技术国防重点学科实验室 哈尔滨 150001）

2（四川大学 水利水电学院 成都 610207）

文丘里式气泡发生器工作特性分析

居晓峰1孙立成2唐文偲1运红宇1阎昌琪1

1（哈尔滨工程大学 核安全与仿真技术国防重点学科实验室 哈尔滨 150001）

2（四川大学 水利水电学院 成都 610207）

气泡发生器是钍基熔盐堆脱气系统的关键部件，其功用为将载气碎化成尺寸均匀的小气泡。本文在脱气系统水实验回路实验研究基础上，采用数值模拟方法，应用SIMPLEC算法对标准的k-ε湍流模型和多相流混合模型进行耦合求解，分析了沿气泡发生器流动方向的气液两相流场速度变化、压力变化、湍动能分布规律。沿流向的速度分布表明，气相从喉部开始沿壁面流动，包围位于中心区域的水相，气相速度在扩张段入口处明显降低，速度梯度的变化形成剪切，使得气相破碎、分裂；压力分布表明，在气泡发生器的扩张段入口附近出现了压力梯度的峰值，与实验中测得的气泡集中碎化的位置相近，说明压力的迅速回升可能加速了气泡的碎化；湍动能分布表明，扩张段出口湍动能相对较大，说明此处气液两相能量交换强烈，产生强烈的剪切应力，使气液两相彼此剪切、破碎。以上结果说明，扩张端入口处由于较大的速度梯度及湍动能峰值，导致产生巨大的剪切应力，使气泡出现集中破裂现象。

熔盐堆，气泡发生器，气泡碎化，数值计算

在熔盐堆运行过程中，会不断产生中子吸收截面较大的裂变气体，如氙、氪等，它们的存在严重影响到反应堆的运行。熔盐堆的脱气系统向燃料盐中以气泡形式连续通入一定含量的载气，通过传质过程吸收裂变产生的氙和氪。富含裂变产物气体的载气气泡，通过脱气回路中的分离器从熔盐中分离，从而达到连续从熔盐燃料中去除氙和氪的目的[1]。作为熔盐堆脱气系统的一个重要设备，气泡发生器的作用就是将注入到燃料中的载气碎化成一定尺寸且大小均匀的小气泡。

湍流中气泡破裂的理论首先由Kolmogorov和Hinze提出并发展。Hinze[2]认为在高雷诺数情况下，如果气泡表面所受压力波动的影响超过了气泡表面张力的影响，气泡就会破裂；Fujiwara[3]利用高速摄影对文丘里管内的气泡碎化现象进行了研究；Nomura[4]则分析了文丘里管内气泡碎化的过程与喉部声速的关系。目前，对于气泡发生器中气泡相关研究很少。本文主要针对小型钍基熔盐堆所设计的文丘里式气泡发生器，结合实验中获得的高速摄像资料，分析沿气泡发生器流动方向的各断面气液两相流场速度变化、压力变化、湍动能分布规律，对我国熔盐堆的研发设计有一定参考价值。

1 实验系统及结果分析

1.1 实验系统简介

本文实验结果均源自作者所在项目团队的前期工作，现对实验系统和气泡发生器做简要说明。图1所示为实验系统图，实验以空气和水为工质，水箱中的水通过离心泵的驱动进入气泡发生器入口，空气经储气罐进入气泡发生器喉部，在扩张段气泡碎化为大量微小气泡，随水流出气泡发生器。

1.2 气泡发生器的结构

图2为文丘里式气泡发生器的结构示意图，水从气泡发生器入口进入，气体则首先进入一个注气环腔，环腔通过15个均匀分布的1 mm小孔与文丘里管喉部相通，气体通过这些小孔进入到文丘里管喉部。

气泡发生器的关键结构参数主要包括收缩角、喉部直径、扩张角等。气泡发生器的几个尺寸的大小直接影响气泡的产生和大小，而这些尺寸一般是通过实验或者经验公式来确定。为了节约设计时间及减少实验费用可考虑用FLUENT来进行模拟，然后根据模拟结果进行改进。

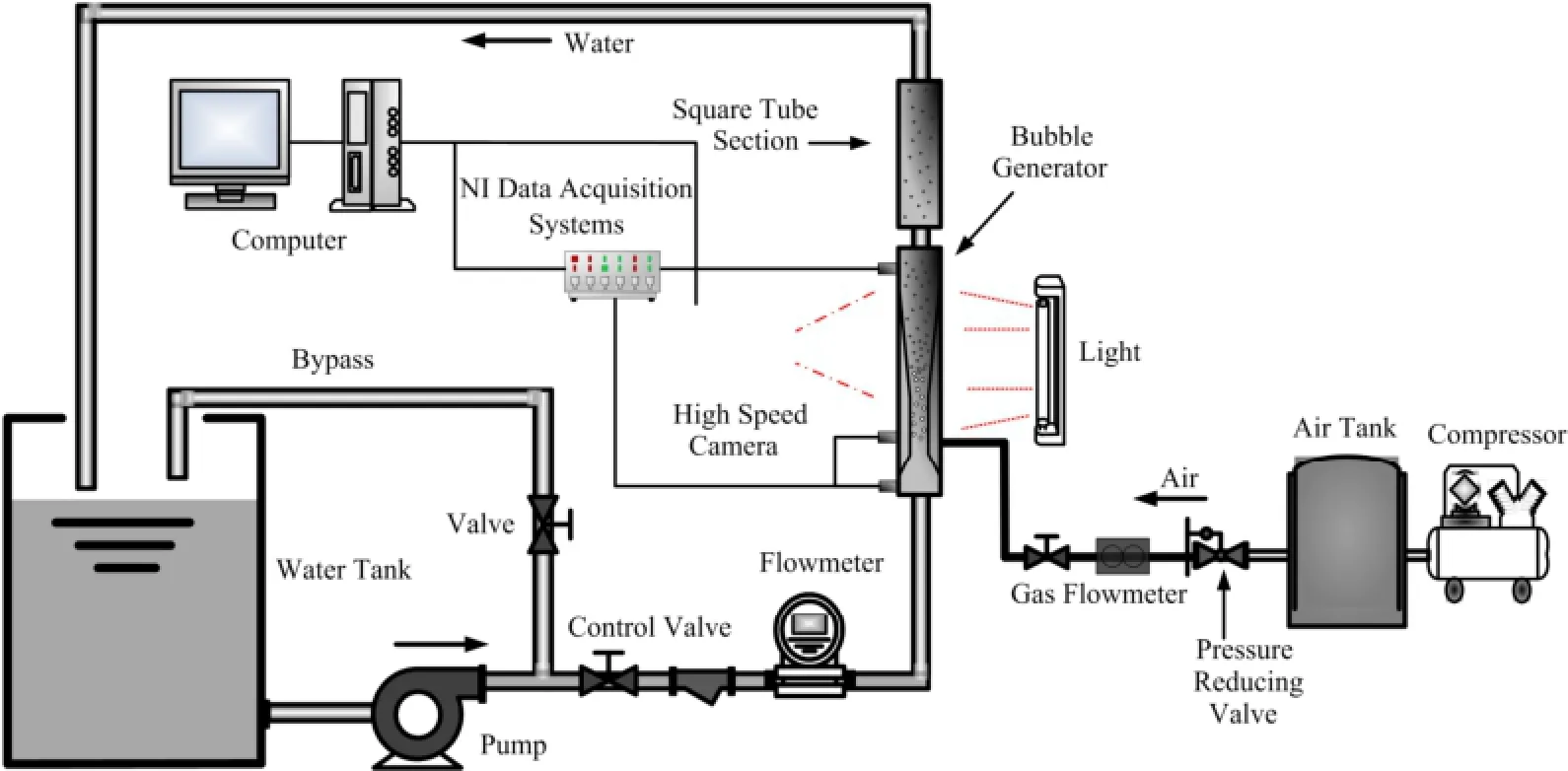
图1 实验系统图Fig.1 Schematic diagram of the experimental system.

图2 文丘里式气泡发生器结构图Fig.2 Structure of the Venturi-type bubble generator.

1.3 控制方程

混合模型是一种简化的多相流模型，它用于模拟各相有不同速度的多相流，它假定了在短空间尺度上局部的平衡，来求解混合相的动量、连续性和能量方程，第二相的体积分率以及滑移速度和漂移速度。由于模型简单，计算量小且结果较为可靠而得到了较多应用。本文采用两相混合模型建立控制方程。

1.4 连续性方程

1.5 动量方程

2 气泡发生器内部流场的三维数值模拟

2.1 几何建模、网格的划分及无关性验证

根据实验中气泡发生器的结构形式及尺寸，用三维建模软件UG建立其完整的几何模型，如图3所示，支管的作用是均匀的向喉部内通入气体。采用六面体网格得到的网格结构如图4所示（网格划分工具为ICEM CFD），划分网格的主要难点在14根支管与喉部相连处，本次划分先划分喉部与支管的部分，最后进行拉伸，网格的质量指标如表1所示。另外，喉部及扩张段内的区域是本文的研究重点，所以进行了加密。

图3 气泡发生器的几何模型Fig.3 Geometric model of the bubble generator.

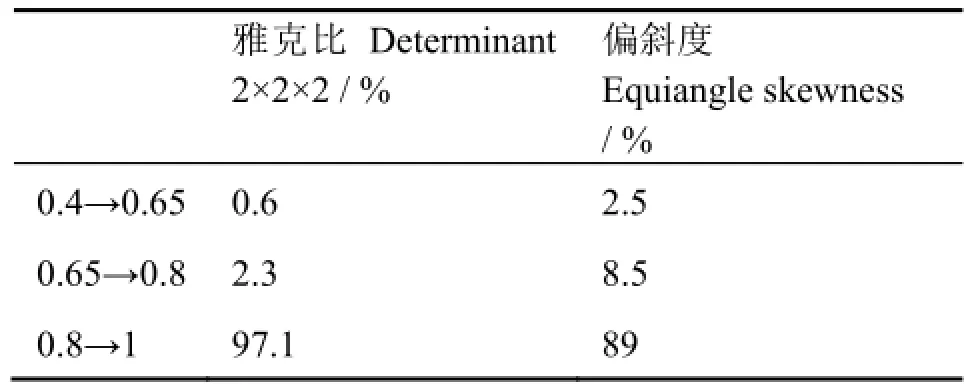
表1 网格质量分布Table 1 Distribution of mesh quality.

网格划分的密度对数值计算结果的影响很大，一般情况下，只有当网格密度增加到一定程度后，使得计算结果随网格数的增加变化很小时，数值模拟计算的结果才有意义。根据网格敏感性分析所得结果加密划分的网格，得到三套不同尺度的网格Coarse、Medium、Fine，网格数分别为726128、1204432、2497226。计算得到的压力与速度沿气泡发生器轴向的分布如图5所示。可以看出，Coarse网格所得的计算结果与Medium的结果有一定误差，而Medium与Fine的计算结果几乎重合。在Medium的基础上继续加密网格对计算结果的影响已经可以忽略。因此，选用Medium网格。

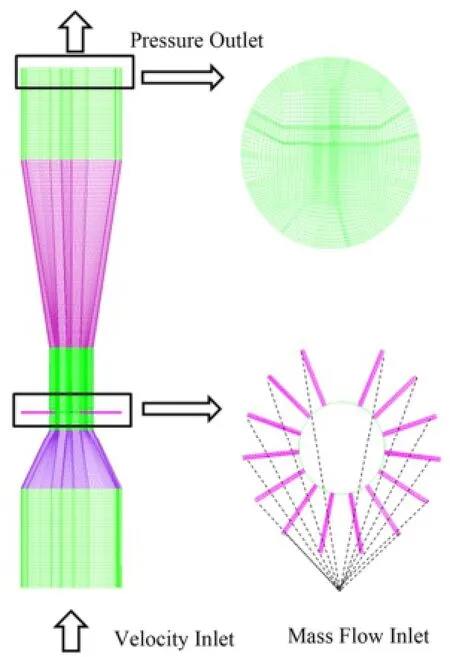
图4 气泡发生器的网格划分Fig.4 Mesh generation of the bubble generator.

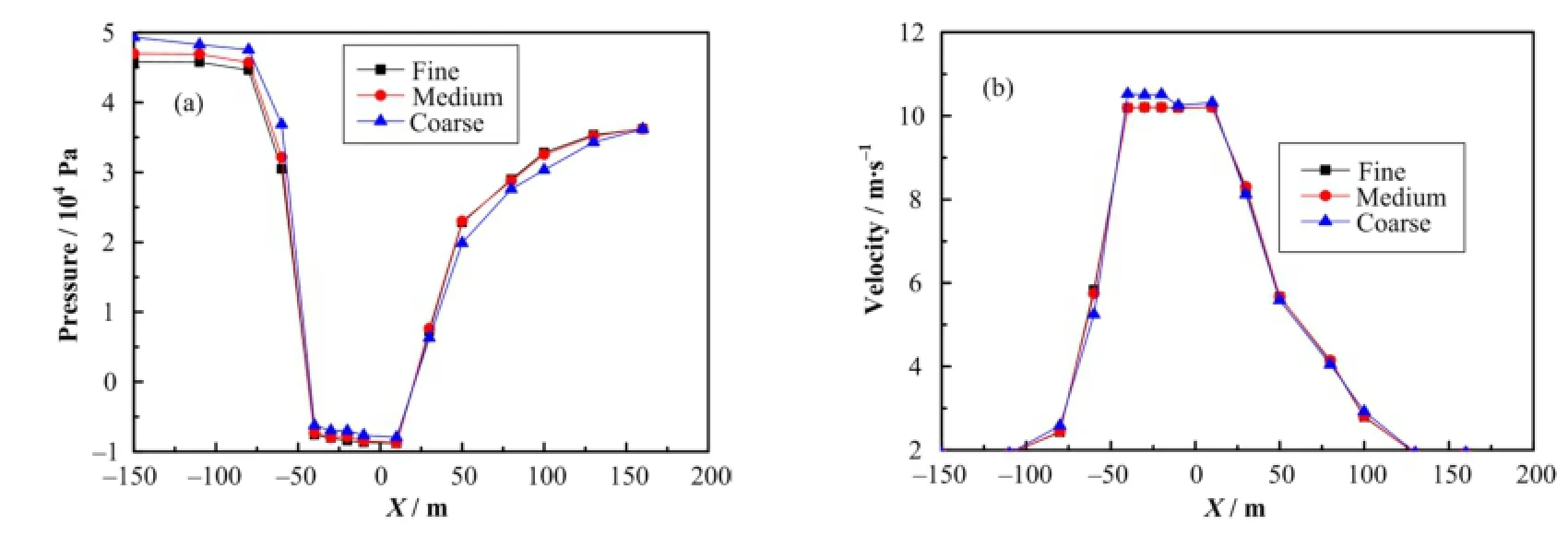
图5 不同密度网格所得压力(a)和速度(b)分布对比Fig.5 Comparison of the pressure (a) and velocity (b) distribution from different grid densities.

2.2 数值模拟边界条件

气泡发生器入口为速度入口，出口为压力边界，进气口设为质量流量入口，两相之间为无滑移条件。设置边界条件时，在湍流定义方法中选择湍流强度与水力直径。在湍流强度中按式(3)进行计算：

对于水力直径，则按照文丘里管的入口直径来确定。对于固壁处采用标准壁面函数处理，壁面相对于混合流体无滑移，工作介质水的密度为998kg·m-1。假设次相空气的直径为0.1 mm，空气密度为1.225 kg·m-3。采用控制体积积分法离散控制方程，采用压强连接的隐式修正SIMPLEC算法进行求解。用非稳态算法，时间步长设为0.005 s，经过2000次迭代，经过10 s运算，残差收敛至10-4以下，位于扩张段入口的监视参数压力、混合速度和空泡份额均已趋于稳定。

2.3 模型校验

不同入口水流量条件下进出口压降值与实验值对比结果如图6所示。标准的k-ε模型计算值与实验值的平均误差仅为8.9%，虽然在较低水流量时，标准的k-ε模型偏差稍大，但在较高水流量时与实验值符合很好。文丘里气泡发生器的工作流量范围处于高水流量范围(16-20 m3·h-1)，因此数值分析选用标准的k-ε模型。

2.4 数值模拟结果与分析

2.4.1 速度分布

从图7-9可直观看出，气泡发生器内部流场速度分布，气流在支管入口处被卷吸进入气泡发生器，在支管与喉部连接处，因水相与气相存在较大速差，低速气流与高速水流碰撞而被瞬间加速。气泡发生器内部流场速度分布显示，喉部内流速最高，在扩张段的近入口处速度梯度非常大。速度剖面呈典型的管内流动特点，而进入扩张段时过流断面不断扩大，流速逐步降低。从沿轴向截面的速度云图可以发现，在近扩张段入口处，两相在径向方向的速度梯度较大，但随着气泡的碎化及两相的混合，径向方向的速度趋于均匀。虽然与喉部相连的14根支管并不呈中心对称，但是由于空泡份额太小（小于0.3%），气相对于整体流场的影响十分微小，因此径向速度分布大致呈中心对称。对比混合相在轴向、径向上的速度分布特征，可以看出，两相流动以轴向为主，在发展过程中因湍动剪切作用，径向不均匀分布程度逐渐减小，在扩张段尾部，两相已处于较好的混合状态。

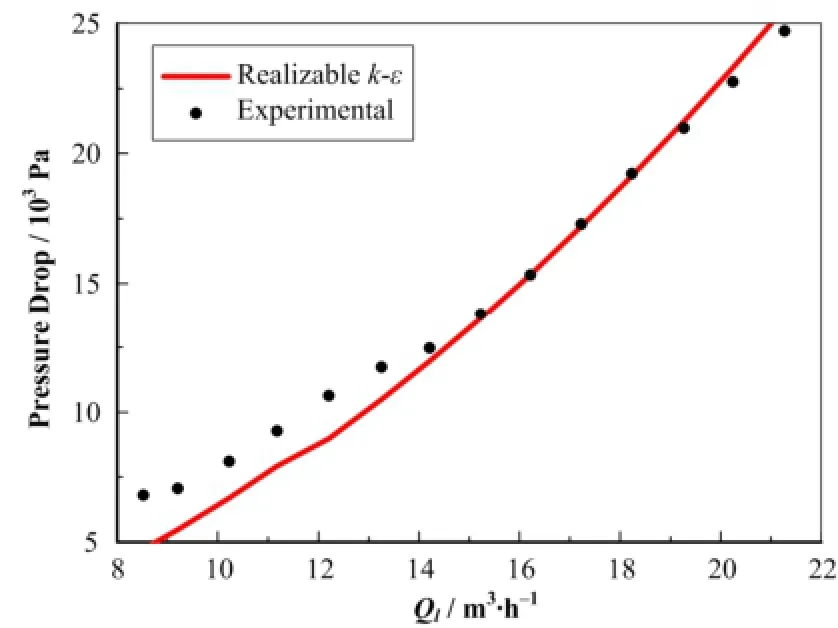
图6 进出口压降的实验与计算值对比Fig.6 Comparison of the pressure drop between the CFD results and the experimental data.

图7 气相的速度云图Fig.7 Contour of velocity of the air.

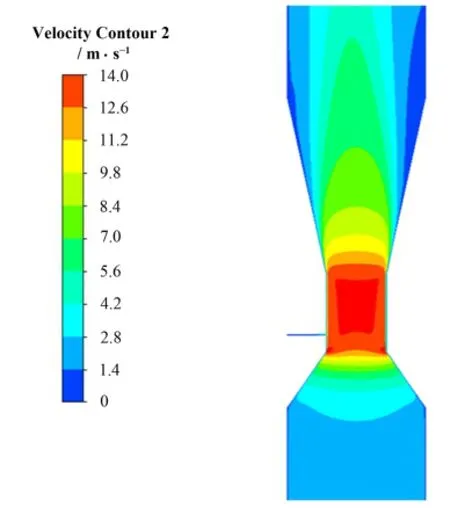
图8 混合相的轴向速度云图Fig.8 Contour of velocity of the mixture in the axial direction.

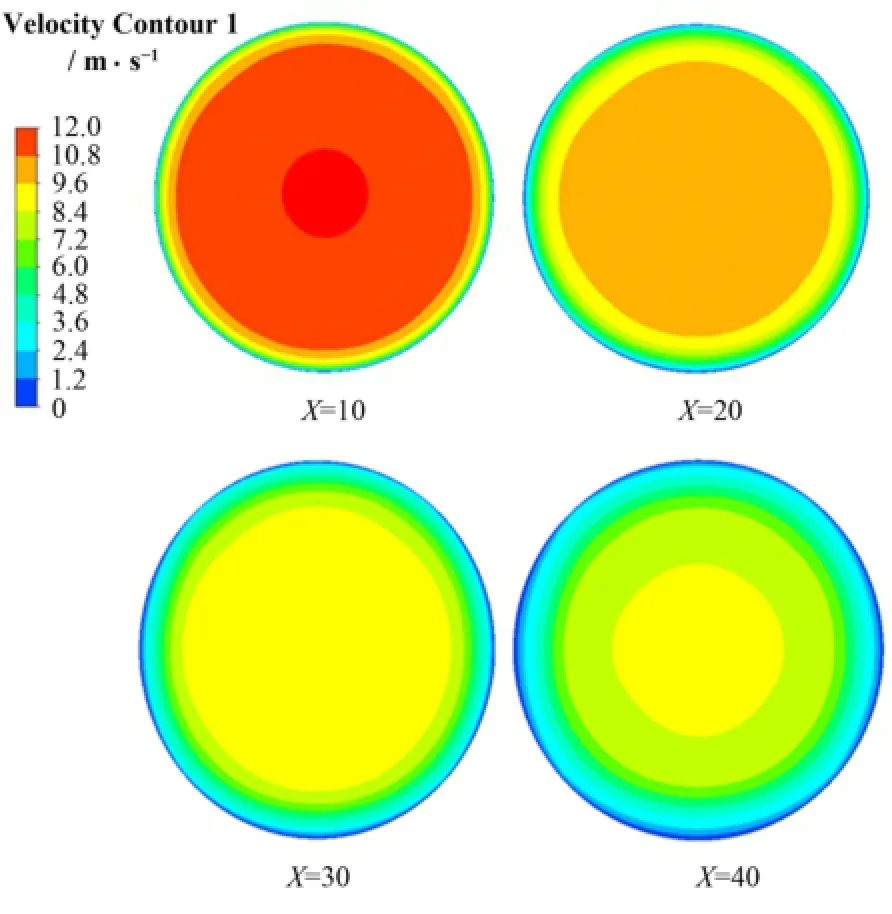
图9 混合相的径向速度云图Fig.9 Contour of velocity of the mixture in the radial direction.

2.4.2 压力分布

由图10可见，在收缩段由于流动截面变小，流速增加，压力减小，在喉部压力基本保持不变，进入扩张段。从图11可以看出，在气泡发生器的收缩段出口以及在扩张段入口，均出现了压力梯度的峰值，而如图12所示，在实验的高速摄像中测得气泡碎化集中在距离扩张段入口10 mm左右[6]，压力梯度的峰值也恰巧在这个位置附近，说明压力的迅速回升可能加速了气泡碎化的过程。

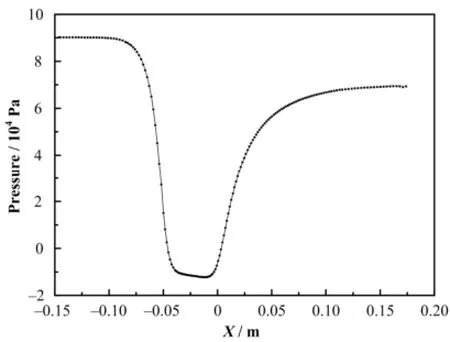
图10 沿轴向的压力分布Fig.10 Pressure distribution in the axial direction.

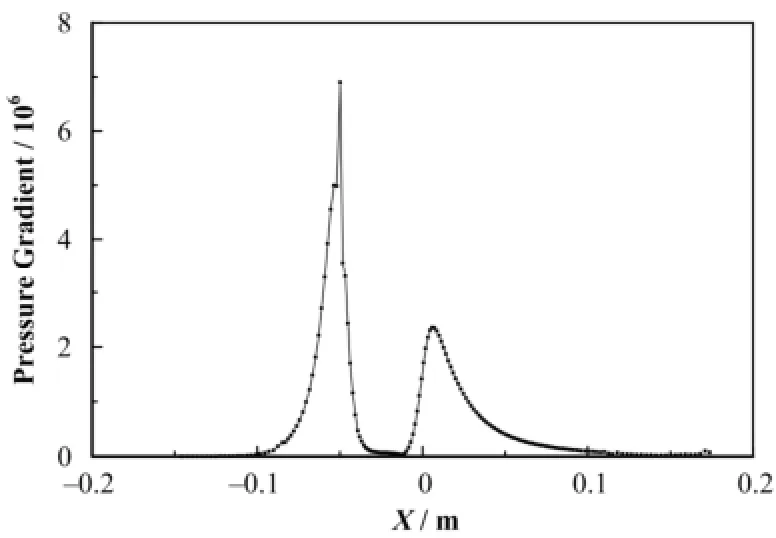
图11 沿轴向的压力梯度分布Fig.11 Pressure gradient distribution in the axial direction.

图12 气泡发生器气泡碎化集中位置的测量Fig.12 Location of intensive breakup of bubbles in the bubble generator.

2.4.3 湍动能分布

如图13所示，在扩张段入口产生了湍动能的峰值，这个峰值是由于扩张段截面面积突然增大以及气液两相的能量交换引起的。在实验中气泡的碎化主要分布在离扩张段入口10 mm左右，这与图7中的湍动能峰值位置相近，说明强烈的湍动能产生了强烈的剪切应力，使气液两相彼此剪切，迅速破碎。

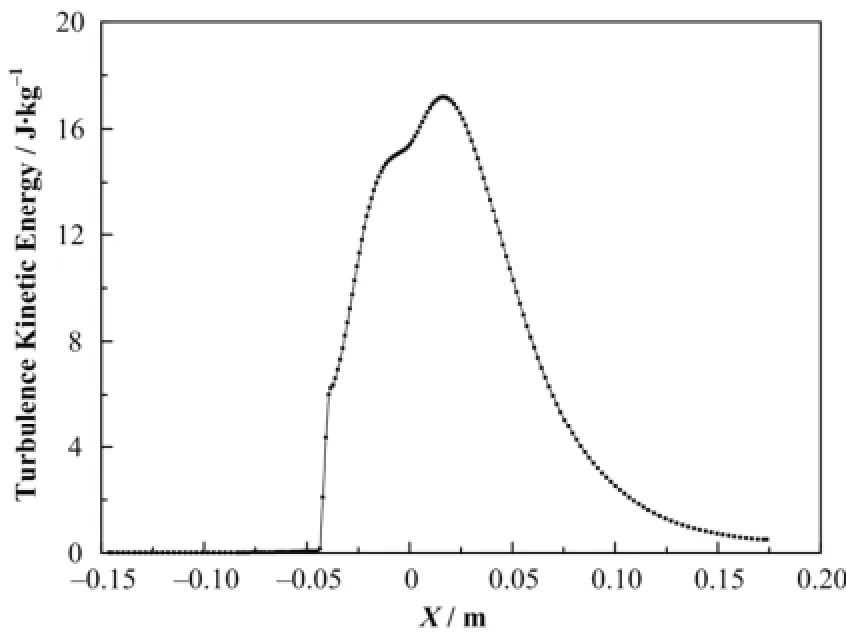
图13 气泡发生器沿流向的湍动能分布Fig.13 Turbulent kinetic energy distribution along the flow direction in the bubble generator.

3 结语

本文在脱气系统水实验回路实验研究基础上，采用数值模拟方法，运用标准k-ε湍流模型和多相流的混合模型，采用SIMPLEC算法进行耦合求解，分析了沿气泡发生器流动方向的各断面气液两相流场速度变化、压力变化、湍动能分布规律。

(1) 沿流向速度分布表明，高速运动的水流卷吸了喉部较低速度的气相一起流动，气相速度迅速增大，沿壁面流动，包围位于中心区域的液相。在近扩张段的入口处，两相在径向方向的速度梯度较大，但随着气泡的碎化及两相的混合，径向方向的速度趋于均匀。

(2) 压力分布表明，在气泡发生器近扩张段的入口处出现了压力梯度的峰值，与实验中测得的气泡集中碎化的位置相同，说明压力的迅速回升可能加速了气泡碎化的过程。

(3) 湍动能分布表明，近扩张段的入口处湍动能相对较大，较大的湍动能表明气液两相能量交换强烈，强烈的湍流能产生强烈的剪切应力，使气液两相彼此剪切、破碎，并充分混合。

1 Robertson R C. MSRE design and operation report I[R]. ORNL-0728, U.S. Atomic Energy Commission, 1965: 205-243

2 Hinze J O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes[J]. American Institute of Chemical Engineers, 1955, 1(3): 289-295

3 Fujiwara A. Bubble breakup phenomena in a Venturi tube[C]. San Diego, California USA, 2007

4 Yasumichi N. Study on bubble breakup mechanism in a Venturi tube[C]. Hamamatsu, Shizuoka, Japan, 2011

5 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2011 WANG Fujun. The analysis of computational fluid dynamics[M]. Beijing: Tsinghua University Press, 2011

6 唐文偲, 阎昌琪, 孙立成, 等. 文丘里式气泡发生器气泡碎化特性研究[J]. 原子能科学技术, 2014, 48(5): 845-848 TANG Wencai, YAN Changqi, SUN Licheng, et al. Characteristics of bubble breakup in venturi-type bubble generator[J]. Automic Energy Science and Technology, 2014, 48(5): 845-848

CLCTL334

Analysis of the operating characteristics of a Venturi-type bubble generator for MSR

JU Xiaofeng1SUN Licheng2TANG Wencai1YUN Hongyu1YAN Changqi1
1(Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin 150001, China) 2(College of Hydraulic and Hydra-electric Engineering, Sichuan University, Chengdu 610207, China)

Background: Bubble generator is a key device in the off-gas removal system of the molten salt reactor (MSR) for breaking up the carrier gas into tiny bubbles. Purpose: The distribution rules of velocity, pressure and turbulent kinetic energy along the flow direction of the Venturi bubble generator were analyzed with the software FLUENT. Methods: Based on the experimental water loop with the target bubble generator, numerical simulation using FLUENT was performed. Both the multiphase model (Mixture), standard k-ε turbulent model were adopted and the SIMPLEC method was employed to get the coupled solutions. Results: The distribution of velocity along the flow direction shows that the air is entrained by the water flew in the throat section and the air flew close to the wall of the generator. The speed of air is reduced significantly in the diverging portion of the bubble generator. The velocity gradient creates great shear stress, making the bubbles break up. The distribution of pressure shows that the peak of the pressure gradient appears at the entrance of the diverging portion of the bubble generator. The numerical results are very close to the data in the experiment, which indicates that the quick recovery of pressure may accelerate the breakup of bubble. The turbulent kinetic energy peaks at the entrance of the diverging portion of the bubble generator, which suggests that strong energy exchange there, resulting in strong shear stress to break up the bubbles. Conclusion: The large velocity gradient and the peak of turbulent kinetic energy at the entrance of the diverging portion of the bubble generator cause great shear stress, which is the reason for the bubble breakup taking place intensively there.

Molten salt reactor (MSR), Bubble generator, Bubble breakup, Numerical study

TL334

10.11889/j.0253-3219.2014.hjs.37.120605

项目(No.51376052)、 四川大学科研启动基金(No.YJ201432)资助

居晓峰，男，1989年出生，2012年毕业于南京工程学院，现为硕士研究生，研究方向为反应堆热工水力

孙立成，E-mail: leechengsun@sohu.com

2014-08-11，

2014-09-07