基于尖点突变模型的中国省域能源强度差异的实证分析

叶翠红，赵玉林

(1.华中科技大学经济学院，湖北 武汉 430074；2.武汉理工大学经济学院，湖北省科技创新与经济发展研究中心，湖北 武汉 430070)

1 引言

作为能源效率和经济发展质量的核心指标，降低能源强度是处于转型期的中国解决经济发展与资源环境约束矛盾所追求的核心目标之一。相关研究表明，资源禀赋、能源消费结构、对外开放程度、能源价格、FDI、市场竞争等因素均会影响能源强度演变的方向和强度。而与能源强度相关的各因素都是通过影响产业结构或各产业能源使用效率的变化进而间接地影响能源强度的变化［1］。技术进步、产业结构优化分别通过提高部门的能源利用效率、促进能源更多地从高能耗部门流向低能耗部门，成为影响能源强度变动的两大主导因素。基于此，学术界形成了能源强度变动的产业结构主导论［2-3］和技术进步主导论［4］两大派别。而产业结构、技术进步对不同区域能源强度的影响存在着差异［5-6］。

可以看出，各因素与能源强度相互作用的多层次性决定了产业结构优化、技术进步与能源强度之间存在着复杂的非线性作用关系。已有的因素分解、投入产出、回归分析、因果检验等方法多用来分析各因素对能源强度的影响程度，在解释影响因素与能源强度的内在作用机制和非线性关系时显得比较薄弱。本文拟运用随机尖点突变理论这一新的视角对中国省级区域产业结构优化、技术进步与能源强度的内在非线性关系进行实证检验，并揭示能源强度演变的突变机理和规律。

2 能源强度随机尖点突变模型的构建

自20 世纪70年代初法国数学家托姆创立突变理论以来，突变论已被成功地应用到了经济领域，包括对商业周期［7］、企业竞争行为［8］、股市价格变动［9］等方面的研究，为经济领域中动态的、非线性的、多变量决定的突变现象的研究提供了有效的数学模型［10］。尖点突变作为经典突变模型中较为简单、内涵丰富的一种，在现实中应用最多。随机尖点突变则是经典突变理论由研究确定性系统向研究随机影响下的系统的一种发展。Grasman等［11］开发的cusp 程序包具有可以设置初始值、允许参数值被约束、比较模型优劣、计算机运行更为便捷等优势，为随机尖点突变理论的实证检验提供了重要的工具。本文运用随机尖点突变理论构建模型，并运用cusp 程序包进行尖点突变模型的估计。

假设能源强度在产业结构优化水平和技术进步水平作用下的演变具有尖点突变特征，则随机影响下的能源强度的尖点突变机制可以用随机微分方程表示为:

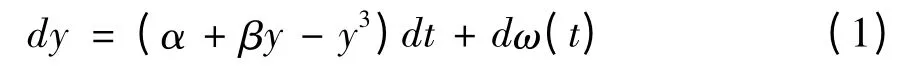
其中y 为尖点模型中的状态变量即能源强度，α 和β 为控制变量，分别表示正则因子和分歧因子，决定了系统的特有结构，dω (t)表示随机误差。设Y 为能源强度的实际状态变量，则y=ω0+ω1Y;设X1和X2分别为产业结构优化水平和技术进步水平，则α=α0+α1X1+α2X2，β=β0+β1X1+β2X2，其中α0、α1、α2、β0、β1、β2分别为正则因子和分歧因子中独立观测变量的平滑转化系数。尖点突变模型系统所有的稳定均衡点满足

对于随机过程(1)，当t→∞时有一个极限概率密度函数:

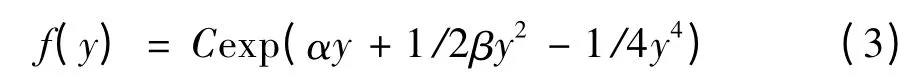
针对f (y)运用类牛顿极大似然化方法进行迭代可以得到参数α0、α1、α2、β0、β1、β2、ω0、ω1的最优拟合值。本文借助R 软件的cusp 程序包，设α0、α1、α2、β0、β1、β2、ω0、ω1中的若干参数值为零(比如若设α1=0，意味着产业结构优化水平对正则因子没有影响)，逐个运行含有约束的拟合模型，以AIC 和BIC 为模型优度的判别准则(AIC、BIC 越小越好)并结合其他统计量寻求能源强度演变与产业结构优化水平、技术进步水平之间关系的最优解。

3 中国能源强度尖点突变的实证分析

3.1 数据来源及处理

本文拟以除西藏之外的30 个省域(省、直辖市、自治区，简称为“省”)及全国2010年、2011年数据为样本对中国能源强度的尖点突变模型进行检验(西藏由于数据缺失较多而未列入研究范围，文中全国数据中的原始数据均为除西藏之外的30 个省域数据的加总)。文中所需原始数据主要来自《中国统计年鉴》、《中国能源统计年鉴》、《中国高技术产业统计年鉴》、《中国工业经济统计年鉴》及各省统计年鉴相应年份的统计值。

首先计算出各省及全国的能源强度即单位GDP 能源消费总量，其中GDP 数据以1999年为基期进行了不变价处理。各省及全国产业结构的优化水平用其高技术产业总产值在制造业产值中的比例计算得到，其中制造业产值数据由各省21 个制造业的工业总产值求和取得。全要素生产率不能通过统计数据直接取得，本文以GDP 作为产出，资本和劳动力作为投入，用DEA 方法测算中国及各省2010、2011年的Malmquist 生产率指数。劳动力投入使用就业人员数据，资本投入则使用以永续盘存法计算的固定资本存量数据，公式为:

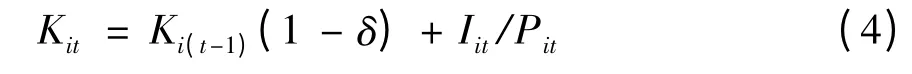
其中i 表示省份，t 表示年份，I 为当年价格的固定资产新增投资额，P 为当年对基期的固定资产投资价格指数，δ 为固定资产折旧率。本文以中国经济增长与宏观稳定课题组［12］估算的1999年各省固定资本存量作为基期存量(该文1999 全国省域固定资本存量的估计结果是以1978年为基期的估算，而本文的新增固定资产投资额是以1999年为基期进行不变价处理的数据，所得到的固定资本存量估计结果不影响省际TFP 的相对大小)，各省固定资产新增投资额亦参照其计算方法。固定资产投资价格指数调整为以1999年为基期的价格指数，δ 选取通常意义上使用较多的5%。

为消除变量间的量纲关系，运用Z 标准化方法分别得到的能源强度、产业结构优化水平、全要素生产率数据进行标准化处理，作为随机尖点突变模型拟合的数据基础。

3.2 尖点模型拟合结果

运用R 软件对中国2010年、2011年30 个省及全国的能源强度、产业结构优化水平和技术进步的数据进行尖点模型的拟合。假设正则因子、分歧因子均至少与一个独立观测变量相关，设置若干参数值为零，可以得到72 次模拟结果，2010年、2011年各得到10 个AIC 和BIC 均小于对应的线性模型和逻辑模型的尖点模型(见表1)，表明能源强度在产业结构优化、技术进步满足一定条件时会表现出尖点突变特征。

在2010年的十个模型中，cusp2 和cusp10 的AIC 和BIC 相对较小，由于二者AIC 和BIC 的大小表现不一致，此时参考拟合优度指标(R2)和似然函数对数值的大小，得到cusp2 的拟合效果最优，cusp2 的卡方似然检验也表明在正常误差内尖点模型比线性模型更好(X-squared=25.76，df=2，p-value=2.552 ×10-6)。2011年的十个模型中cusp1 和cusp10 的AIC 和BIC 相对较小，二者AIC 和BIC的大小表现也不一致，同样参考拟合优度指标和似然函数对数值的大小，得到cusp1 的拟合效果最优，其卡方似然检验也表明在正常误差内尖点模型比线性模型更好(X-squared=31.35，df=2，p-value=1.557 × 10-7)。可以看到，2010年、2011年拟合效果最优的两个模型对于参数的约束是一致的(α2=0，β1=0)，进一步验证了能源强度与产业结构水平、技术进步水平变量间作用关系的相对稳定性。

表1 能源强度的尖点拟合模型

续表1

2010、2011年拟合效果最优的尖点突变模型的参数估计值及其统计量见表2。表2 显示除β2外其他系数均显著不为0。参数α0、α1、β0、β2、ω0、ω197.5%的置信区间2010年为(-3.37，-0.74)、(-3.27，-0.57)、(0.92，3.26)、(-0.73，0.54)、(-1.68，-1.10)、(0.76，1.16)，2011年为(-3.86，-0.89)、(-3.64，-0.76)、(0.93，3.32)、(-0.78，0.49)、(-1.73，-1.17)、(0.79，1.16)，均覆盖了估计值。

结果显示，能源强度在产业结构优化水平和技术进步水平满足一定条件时表现出尖点突变特征。与正则因子相关的变量是产业结构优化水平，二者呈现出负相关关系;与分歧因子相关的变量是技术进步水平，二者也呈现出负相关关系，验证了能源强度在产业结构优化、技术进步变量影响下的突变机制。

3.3 结果分析

根据实证结果，能源强度在产业结构优化、技术进步作用下可能发生突变，突变机制如图1 所示，其中均衡曲面的上叶和下叶分别代表能源强度的两种稳定均衡态，中间阴影叶上的点是能源强度的不稳定均衡态。根据经典尖点突变理论的 一般原理，能源强度的演变具有以下特点和规律。

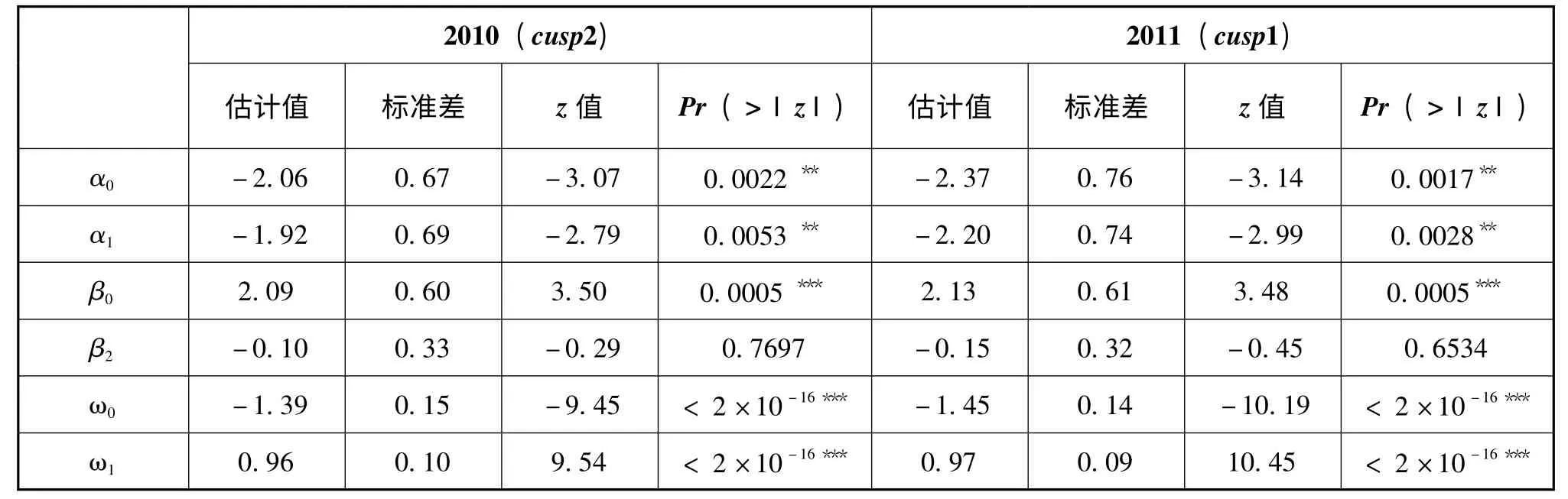
表2 2010、2011年最优模型参数估计值及其统计量

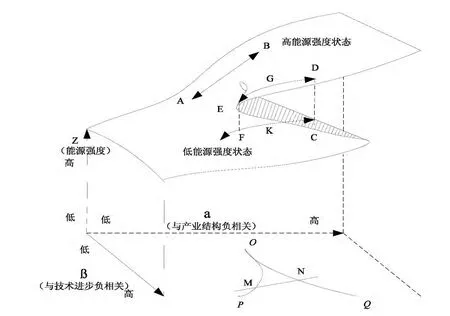
图1 能源强度突变的尖点模型

(1)能源强度的演变具有尖点突变特征，产业结构优化水平决定能源强度突变的正则因子，技术进步水平决定能源强度突变的分歧因子。在区域能源强度演变过程中，当技术进步水平较高，分歧因子较小，随着产业结构优化水平的稳步提升，能源强度会不断下降;当技术进步水平较低，技术进步成为能源强度演变的不稳定因素，产业结构优化水平的连续变化对能源强度可能产生不连续的影响。技术进步水平越低，能源强度的演变越不稳定。

(2)能源强度在一定条件下能够分叉出两个不同的稳定均衡态，该分叉是能源强度在产业结构优化和技术进步变量共同作用下产生的一种自组织突变现象。当产业结构优化、技术进步变量决定的控制参数穿越分歧集合临界线(27α2-4β3=0)，能源强度的均衡态会自发地产生突变，自变量沿不同方向变化发生的突变点是不同的。假设技术进步水平不变，产业结构优化水平沿着控制平面中的直线MN 变化，当与临界线OP 或OQ相交时，能源强度会产生突变;对于低能源强度状态，当产业结构优化水平由高变低(由M 向N)，能源强度的突变发生在与OQ 相交处，自发地由C 突变至D;反过来，对高能源强度状态，当产业结构水平不断提升，能源强度的突变发生在OP 处，由E 突变至F。当27α2-4β3＜00，能源强度存在两个稳定均衡点和一个不稳定均衡点，初始状态、自变量的变动方向和大小决定能源强度所处的稳定状态。

(3)能源强度在产业结构优化和技术进步作用下的自组织突变具有不可逆性。假设初始状态为高能源强度状态D，技术进步水平不变，产业结构优化水平由低向高变化时，能源强度会平缓经由G 减小到E，再由E 突跳至F。此时即使产业结构优化水平降至之前G 点的水平，能源强度也只会由F 平缓增加至K，而不是回到G 点。这表明，能源强度一旦由一种稳态进入到另一种稳态，即使产业结构优化、技术进步再回到之前的水平，能源强度只会在新的状态上微小变动，相对较为稳定。

(4)当控制参数在分歧区域之外，能源强度只有一个均衡态，且与产业结构优化、技术进步呈现出简单的线性连续变化关系。当27α2-4β3＞0 时，能源强度只会随着产业结构优化水平、技术进步水平的连续变化发生渐进式变化。若技术进步水平较高，随着产业结构的不断优化，能源强度会连续减小(如由B 到A);若技术进步水平较低，随着产业结构优化水平的提高，能源强度分别在高能源强度稳态和低能源强度稳态上产生渐变式的减小(如由D 到G、由K 到F)。

4 结论及政策启示

本文对中国省域能源强度随机尖点突变模型进行了检验，结果表明，能源强度、产业结构优化、技术进步之间存在尖点突变机制，产业结构优化水平决定能源强度突变的正则因子，技术进步水平则决定能源强度突变的分歧因子。当产业结构优化、技术进步变量组合下的控制参数在分歧区域外，能源强度与产业结构优化、技术进步之间表现出简单的线性连续变化关系;当控制参数满足分歧临界条件，能源强度会在自组织作用下发生突变，且这种突变具有不可逆性。这对当前中国各区域降低能源强度具有重要的政策含义。

中国各区域能源强度是技术进步、产业结构优化变量共同作用的结果，二者影响能源强度的方式是不同的。产业结构优化水平是中国能源强度省域差异的关键原因。只要分歧因素较小，随着产业结构优化水平的提高，能源强度会稳步降低;即使分歧因素起作用，提升产业结构优化水平也有利于实现能源强度的跨越式降低。因此，当前中国各地政府应通过政策引导，加快产业结构的调整和优化，促进要素更多地流向低能耗低污染产业，实现能源强度的不断降低。

而在不同的技术进步状态下，对产业结构的调整方式应有所不同。对于技术进步水平较低的区域，地方政府可着力于创造条件使产业结构优化水平、技术进步水平组合的控制参数达到突变的临界，实现能源强度跨越式的降低，从质的水平上拉大与其他区域的差距;对于技术进步水平较高的区域，地方政府则可选择渐变的路径，通过逐步提升产业结构优化水平实现能源强度的稳步降低。

长期来看，要使产业结构优化水平对能源强度产生稳定持续的正面效应，提高技术进步水平是中国各省域实现能源强度降低的必由之路。地方政府应加大自主创新力度，提升技术进步水平，为产业结构优化在促进能源强度降低中充分发挥作用提供一个良好的技术环境。

［1］刘凤朝，潘雄锋，徐国泉.基于结构份额与效率份额的中国能源消费强度研究［J］.资源科学，2007，(7):2-6.

［2］Kambara T.The Energy Situation in China［J］.China Quarterly，1992，(131):608-636.

［3］World Bank.Clear Water，Blue Skies:China's Environment in the New Century［M］.D.C.:World Bank，Washington，1997.

［4］齐志新，陈文颖.结构调整还是技术进步?［J］.上海经济研究，2006，(6):8-16.

［5］董锋，龙如银，周德群，李晓晖.产业结构技术进步对外开放程度与单位GDP 能耗-基于省级面板数据和协整方法［J］.管理学报，2012，(4):603-610.

［6］刘畅，崔艳红.中国能源消耗强度区域差异的动态关系比较研究-基于省(市)面板数据模型的实证分析［J］.中国工业经济.2008，(4):34-43.

［7］Varian H R.Catastrophe Theory and the Business Cycle［J］.Economic Inquiry，1979，(17):14-28.

［8］Lange R，McDade S，Oliva T A.Technological Choice and Network Externalities:a Catastrophe Model Analysis of Firm Software Adoption for Competing Operating Systems［J］.Structural Change and Economic Dynamics，2001，(12):29-57.

［9］Barunik J，Vosvrda M.Can a Stochastic Cusp Catastrophe Model Explain Stock Market Crashes?［J］.Journal of Economic，Dynamics &Control，2009，(33):1824-1836.

［10］Rosser Jr J B.The Rise and Fall of Catastrophe Theory Applications in Economics:Was the Baby Thrown Out with the Bathwater?［J］.Journal of Economic Dynamics and Control，2007，(10):3255-3280.

［11］Grasman R P P P，Maas H L J V D.Wagenmakers E J.Fitting the Cusp Catastrophe in R:a Cusp Package Primer［J］.Journal of Statistical Software，2009，32(8):1-27.

［12］中国经济增长与宏观稳定课题组.资本化扩张与赶超型经济的技术进步［J］.经济研究，2010，(5):4-20.