评价贝叶斯向量自回归模型在区域经济预测中的表现

王 飞

(中央民族大学经济学院，北京 100081)

1 引言

传统的区域经济定量预测以经济计量模型为主，根据宏观经济理论建立联立方程组以描述经济变量之间的内在联系。该方法的优点是模型以经济理论为基础，参数具有明确的经济含义。目前，文献中所构建的区域经济预测模型大多采用该方法［1-3］。但经济计量模型的方程组数量多，动辄10～30个方程，参数估计的误差会相互累积影响最终的预测效果。经济计量模型在20世纪70年代末的滞涨时期预测效果不佳，以ARIMA模型为基础的现代时间序列分析逐渐兴起。Sargent和Sim提出了VAR模型［4-5］，扩展到多变量预测。Anderson指出，在区域经济预测方面，理论上VAR模型预测效果要好于经济计量模型，因为经济计量模型需要所有变量的数据，但区域间贸易、投资等数据几乎没有，而VAR模型并不需要全部的数据［6］。从实际应用看，VAR模型在国外区域经济预测中取得了较好的效果［7］。

但随着变量个数的增加，VAR模型中的参数迅速增加以致自由度消耗过快。考虑到我国改革开放前后经济结构发生了巨大变化，区域经济数据大多从1978年开始，数据较少，VAR模型难以保证参数估计精度和预测精度。Litterman提出的贝叶斯向量自回归模型 (BAVR)［8］利用变量的统计性质作为VAR模型参数的先验信息在一定程度上克服了VAR模型的过参数化缺陷。从理论上看，BVAR模型在我国区域经济预测中具有一定的优势。BVAR模型在国外区域经济预测中的初步应用取得了一些成效［9-10］。国内研究中，王飞的研究表明，区域BVAR模型的预测误差要显著小于其他模型［11］。

需要指出的是，绝大多数区域预测模型文献缺乏“真正”意义上的样本外预测误差评价研究。在这些文献中，多是把已知的时间序列数据分成两部分，前一时期的数据称作“样本内”数据，后一时期数据称作“样本外”数据，样本内数据用于构建模型并得到后一时期的预测值，与后一时期的实际值相比得到所谓的“样本外”预测精度［11-13］。显然，这并非真正意义上的预测，只是对实际预测行为的近似，所以也被称作“伪样本外”预测。缺乏真正的样本外预测误差评价，使得我们无法准确衡量一个预测模型的优劣。

王飞等运用BVAR模型预测了民族八省区(五个自治区和青海，贵州、云南)2010—2015年主要经济指标增长率［14］，建模及预测的时间是2010年3月。《中国统计年鉴2013》已经公布了2010—2012年民族八省区主要经济指标的实际数据，这为我们评价区域BVAR模型的真实预测效果提供了一个绝佳的机会。本文将据此评价BVAR模型对于区域经济的实际预测能力，并分析影响BVAR模型预测精度的主要因素，以及改进BVAR模型预测精度的努力方向。

2 BVAR模型预测民族地区宏观经济

BVAR模型是在普通VAR模型基础上发展起来的。考虑如下的无约束VAR模型。

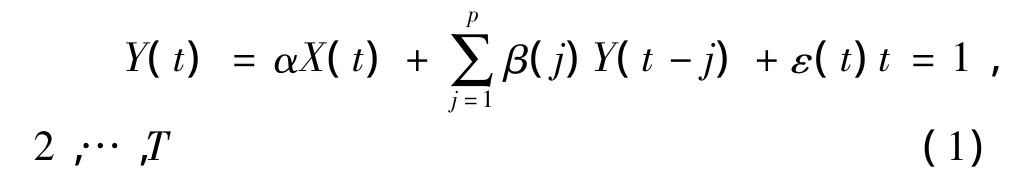
其中，t表示时刻，p表示滞后阶数;Y(t)是K维随机向量Y在时刻t的取值;X(t)是M维列向量，是方程中的外生变量，包括常数项、趋势项等;α是 X(t)的系数矩阵，β(j)是 Y滞后 j期Y(t-j)的系数矩阵;ε(t)是K维随机误差项。

模型 (1)总共有K2p+KM个待估参数，除非观测值很多，VAR模型常面临自由度较少，因而预测精度不高的问题。Litterman提出的BVAR模型［8］将预测者对参数的先验信息与上述无约束VAR模型相结合，从而有效地解决了VAR模型中的自由度问题。Litterman等人提出的先验因首先在明尼苏达大学和美联储明尼苏达分行提出，又被称为明尼苏达先验。

明尼苏达先验中每个参数的先验分布都假定为正态分布，对于外生变量参数α，设定为扩散先验，对于β，由于经济时间序列经常表现出随机游走的特点，明尼苏达先验设定其先验期望是

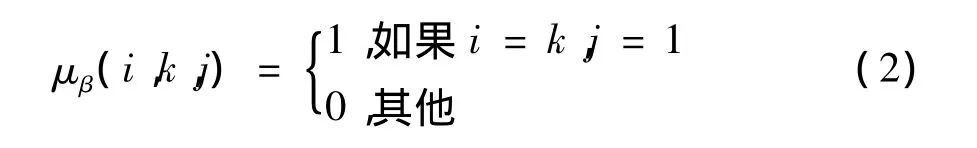
其中，i表示方程组 (1)中第i个方程，k表示Y中第k个变量，而j表示滞后阶数。

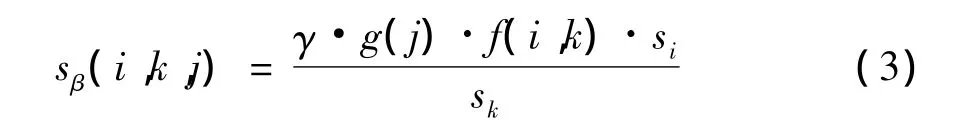
β的先验方差是通过下式予以设定。其中si是第i个方程的单变量自回归的标准误，的目的是消除Y中各变量不同单位的影响。

f(i，k)是相对权重，是 β(i，k，j)与 β(i，i，j)的标准误的比值。g(j)通常设定为谐函数g(j)=j-d的形式，d越大，先验方差随滞后阶数的增加衰减的越快。γ是每个方程中，变量自身滞后一期系数的先验标准误。可见，BVAR模型中，参数先验方差(i，k，j)的设定就转化为所谓的超参数 γ、d和f(i，k)的设定上。

估计BVAR模型需要预测者设定上述超参数取值。因为BVAR模型的主要目的是预测，因此，超参数的确定实际上是一个类似栅格搜索的过程，在超参数取值范围内搜索得到能获得最优预测效果的超参数值。

我们早期的研究建立了BVAR模型来预测2010—2015年民族八省区的地区生产总值、固定资产投资、消费价格指数、社会消费品零售额以及地方财政一般预算收入这五个主要经济变量［14］。BVAR模型中引入了全国GDP和中央政府转移支付 (用地方财政一般预算收支差额来衡量)作为外生变量，来描述民族八省区所受到的中国整体宏观经济波动以及中央财政转移支付的影响。

数据来自民族八省区1978—2009年的年度数据。为了消除价格的影响以及便于各省区之间数据可比，上述变量统一转变为2000不变价的数值。数据按2002年为界分成两个时期，2002年之前的数据用于估计BVAR模型的参数，2002—2009年的数据用于确定BVAR模型超参数值以及最优滞后阶数，确定的标准是最小的超前5步预测值的Theil U统计量。BAVR模型用Winrat软件进行估计和预测。

3 BVAR模型预测民族地区宏观经济

3.1 预测青海经济发展的实际误差分析

我们首先评价BVAR模型对于青海主要经济指标的预测误差。选择青海为例是因为，青海省信息中心每年都会发布下一年主要经济指标的预测值，便于我们做详细的样本外预测误差对比分析。

BVAR模型给出的是增长率 (按可比价格)的预测值，而青海信息中心给出的是名义值 (绝对量)的预测数据，为了能够直接比较，我们计算出两种预测方法的2000不变价绝对量预测值以及增长率预测值 (按可比价格)。两种方法的预测误差见表1，其中不变价绝对量的预测误差用平均绝对百分比误差 (MAPE)以及THeil U统计量来衡量，增长率的预测误差用平均增长率的差异来衡量。需要指出的是，BVAR给出的是超前3年预测，而青海信息中心是超前1年预测，理论上，前者平均预测误差要大于后者。

表1 2010—2012年BVAR模型、青海信息中心预测值与实际值比较

从表1可以看出，BVAR模型预测青海生产总值2010—2012年平均增长率为12．41%，比实际值低1．26个百分点，略优于青海信息中心的预测，而且MAPE、THeil U统计量来衡量的预测误差也都表明对于青海地区生产总值的预测上，BVAR模型的预测误差更小。

但BVAR模型对青海固定资产投资，消费价格指数和社会消费品零售额的预测存在较大误差。对数据详细观察后我们发现，可能受2009年出台的“四万亿”经济刺激计划所致，从2009年开始，青海固定资产投资突然出现大幅加速增长，而2002—2008其年均增长率仅为12%。因为不同于青海信息中心，BVAR模型是超前3年预测，模型没能根据最新数据及时调整固定资产投资的预测值，所以造成BVAR模型预测误差偏大。

青海CPI实际值变化情况与全国CPI变动情况非常接近。我们认为BVAR模型预测青海CPI误差很大的原因在于，模型设定之初未考虑到青海CPI与全国CPI之间的联动关系，属于模型设定上存在先天不足。

至于BVAR模型高估了青海社会消费品零售额，我们认为消费品零售额在很大程度上依赖于消费品价格，因为BVAR模型低估了消费价格指数，因此将会高估消费品零售额。

BVAR模型和青海信息中心对于青海地方财政一般预算收入的预测各有优势。BVAR模型MAPE值较低，而青海信息中心Theil U指数较低，且平均增长率预测误差更小。

可以看出，BVAR模型除了地区生产总值和地方财政收入外，其他指标预测误差较大，明显不如青海信息中心预测准确。但如果考虑到BVAR模型是超前3年预测而非超前1年预测，而且在地区生产总值预测中占有明显优势，BVAR模型对于青海经济指标的预测误差属于可以接受的范围。

3.2 预测整个民族地区经济发展的实际误差分析

我们在表2中进一步分析了BVAR模型对民族八省区整体的预测误差。遗憾的是并没有其他个人或机构发布民族八省区经济指标的预测数据，我们只能与实际数据做对比。表2显示，BVAR模型预测2010—2012民族地区生产总值年均增长率是13．39%，而实际增长率是12．93%，模型高估了不到0．5个百分点，从MAPE数值来看，平均相对误差仅为0．73%，预测效果令人满意。对于固定资产投资，BVAR模型预测的年均增长率是22．85%，比实际值仅高估了2．44个百分点，平均相对误差MAPE值也只有2．46%。对于社会消费品零售额和财政一般预算收入，BVAR模型预测的年均增长率与实际值相比都是仅高估了1个百分点，MAPE值也仅为1．45%和1．86%。

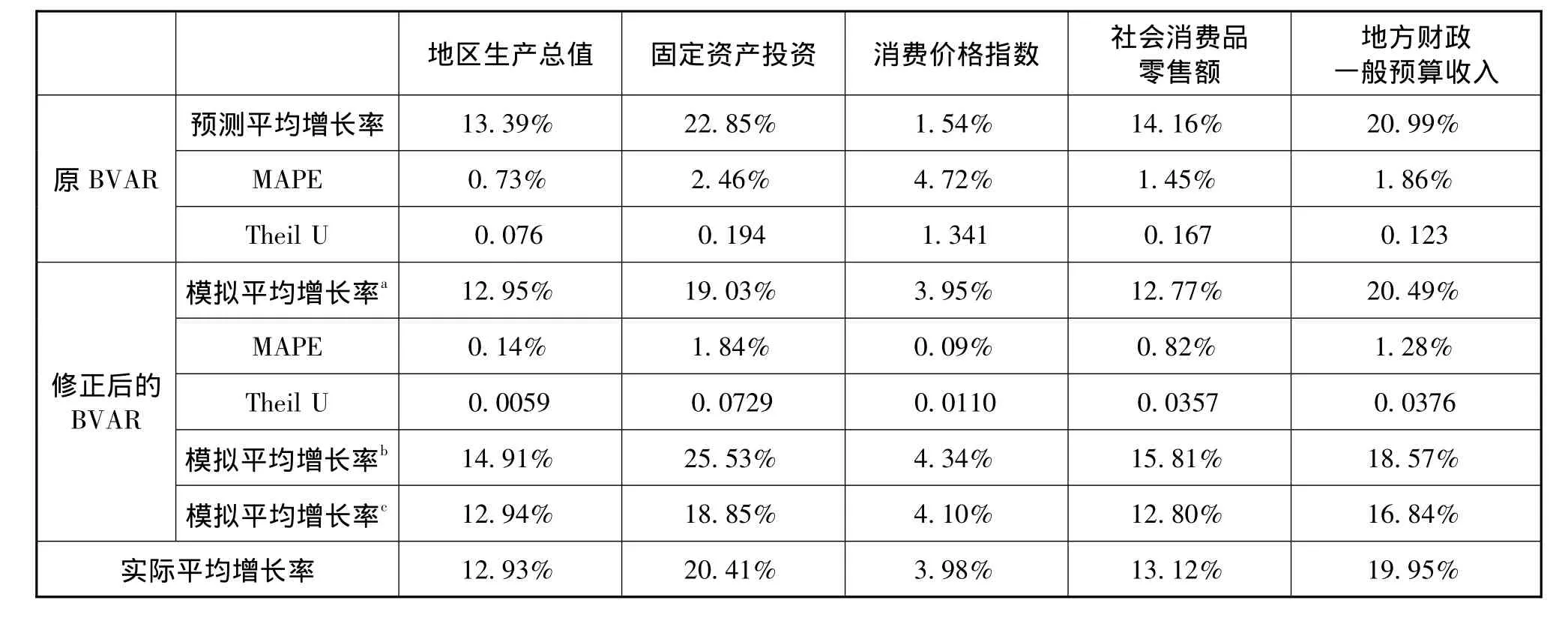
表2 2010—2012年民族地区BVAR模型预测 (模拟)结果与实际值比较

与青海的情况类似，BVAR模型对于民族地区CPI的预测值与实际值相差很大，从Theil U数值也可以看出，模型预测误差比最简单的随机游走模型还要大。其原因同样是BVAR模型在设定时未能考虑到全国CPI对于民族地区CPI的价格传导机制，先天缺陷导致对民族地区CPI预测不理想。

可见，除了消费价格指数外，BVAR模型对民族地区主要经济指标的预测误差非常小，预测能力令人非常满意。如果考虑到BVAR模型是超前3年预测，而且，对于地区生产总值、固定资产投资、社会消费品零售额这三个指标，其预测误差主要来自第三年的预测误差，BVAR模型的短期预测能力令人极为满意。

我们认为BVAR模型对于青海省和整个民族八省区预测效果差别较大的原因在于，青海相对于整个民族地区其经济规模总量很小。从地区生产总值上看，青海省地区生产总值仅占整个民族八省区的3%左右。由于经济规模小，青海更容易受到模型所没有明确考虑的其他因素的影响。相反，整个民族地区经济规模大，经济系统运行的稳定性高，经济运行中的“惯性”更大，受到其他因素的影响相对也更小。因此，BVAR模型对于整个民族地区的预测效果更好。

考虑到最初设定的BVAR模型对于民族地区消费价格指数预测效果差，我们对原BVAR模型进行修正，在除内生变量财政收入的方程外，其他内生变量方程中都增加了全国CPI指数 (2000年=100)作为新增的内生变量，并根据前文所述步骤重新设定BVAR模型中的超参数。2010—2012年的模拟结果见表2中的修正后的BVAR一栏。表2显示修正后的BVAR模型大大提高了民族地区CPI的预测精度，而且其他变量的预测误差也都有一定程度的降低，说明修正后的BVAR模型较为准确地描述了民族地区经济系统的运行规律。

4 民族地区经济发展的决定因素

从表面上看，民族地区属于典型的投资拉动型，2008—2012这五年间，投资占GDP的比重高达83%，而同期全国投资贡献率不到50%。但BVAR模型的脉冲响应函数表明，来自民族地区固定资产投资的冲击对于生产总值几乎没有什么影响。利用修正后的BVAR模型进行模拟，我们发现，民族地区固定资产投资和生产总值主要随着全国GDP变动而变化。如表2所示，2010—2012年如果全国GDP以11%的增速增长时 (比实际增速高约2个百分点)，民族地区固定资产投资同期年均增速将高达25．53%，比实际增速高5个百分点，地区生产总值年均增速将为14．91%，比实际高2个百分点。

全国GDP对民族地区的影响实际上相当于区际出口的作用。民族地区资源性产业比重大，资源类产品民族地区自身需求少，主要是“出口”到东、中部经济较发达地区。全国经济形势高涨时，对资源类产品需求将上升，因此刺激民族地区投资大幅增长，进而带动民族地区经济总量的增长。

另一方面，模拟结果显示，中央政府的转移支付对民族地区经济增长几乎没有作用。如表2所示，2010—2012年如果中央政府转移支付年均增长25%时 (比实际增速高近10个百分点)，民族地区生产总值模拟增长率几乎等同于实际增速。之所以如此，可能是因为中央政府转移支付对民族地区固定资产投资有轻微的挤出效应，同期民族地区固定资产投资模拟增速比实际低1．6个百分点。中央政府转移支付主要作用可能在于降低了民族地区财政增收压力，表2显示民族地区财政收入模拟增速比实际低了3个百分点。

可见，民族地区经济增长属于区际出口拉动型，民族地区自我积累、自我发展能力还不强，不依赖于外部力量难以支撑经济的高速发展。在当前，全国经济增速放缓的新形势下，短期内民族地区还需要维持较高的转移支付，尤其自身发展能力比较弱的西藏、青海、新疆等地区更需如此，尽管转移支付对经济增长作用不大，但可以极大地缓解民族地区各项社会事业支出对财政资金的压力，有利于维持社会稳定和民族团结。长期中则需要进一步调整民族地区产业结构，培育适合民族地区产业结构的创新体系，逐步增强民族地区自身经济实力，实现跨越式发展。

5 结论

本文分析结果表明，对于整个民族地区，BVAR模型对于主要经济指标的预测误差非常小，预测能力令人非常满意。尽管BVAR模型对青海省的预测效果整体上看不如青海信息中心的预测准确，但考虑到BVAR是超前3年预测，而青海信息中心是超前1年预测，BVAR模型的预测误差可以接受。

关于进一步提高预测精度方面，本文研究表明，由于区域经济发展受国家宏观经济形势影响很大，如全国GDP、民族地区转移支付、全国居民消费价格都会对民族地区经济发展施加显著影响。因此，要想准确预测区域经济，需要在模型中设定这些外部影响因素对区域经济的影响机制，并且要能够准确地预测这些外生变量。

同时，民族地区的BVAR模型模拟结果表明，目前民族地区内部市场小，经济增长主要依赖于区际出口，需要进一步调整民族地区产业结构，培育适合民族地区产业结构的创新体系，逐步增强民族地区自我发展的能力，实现跨越式发展。

［1］秦长海，裴毅飞．宁夏宏观经济发展预测模型的建立与应用［J］．资源科学，2006，(04):202-205．

［2］李春雨，刘志彪．区域经济发展与趋势预测研究［J］．统计研究，2002，(11):51-53．

［3］石柱鲜，石圣东，黄红梅．区域型宏观经济模型的开发与预测研究——兼论吉林省“十五”期间经济发展前景［J］．预测，2003，(01):53-56，45．

［4］Sargent T J．Estimation Vector Autoregressions Using Methods Not Based on Explicit Economic Theories［J］．Federal Reserve Bank of Minneapolis Quarterly Review，1979，3，3:8-15．

［5］Sims C A．Macroeconomics and Reality［J］，Econometrica，1980，48(1):1-48．

［6］Anderson PA．Help for the Regional Economic Forecaster:Vector Autoregressions［J］．Federal Reserve Bank of Minneapolis Quarterly Review 1979，3，3:2-7．

［7］Kinal T，J．Ratner．A VAR Forecasting Model of A Regional Economy:Its Construction and Comparative Accuracy［J］．International Regional Science Review，1986，10:113-126．

［8］Litterman R B．ABayesian Procedure for Forecasting with Vector Autoregression［R］．Working paper，Department of Economics，Massachusetts Institute of Technology．1980．

［9］Dua P，D JSmyth．Forecasting USHomes Sales Using BVAR Models and Survey Data on Households'Buying Attitudes for Homes［J］，Journal of Forecasting，1995，14:217-227．

［10］Puri Anil，Gokce Soydemir．Forecasting Industrial Employment Figures in Southern California:A Bayesian Vector Autoregressive Model［J］．The Annals of Regional Science，2001，34(4):503-514．

［11］王飞．贝叶斯向量自回归模型在区域经济预测中的应用——以青海为例［J］．经济数学，2011，28(2):95-100．

［12］肖健华，林健，刘晋．区域经济中长期预测的支持向量回归方法［J］．系统工程理论与实践，2006，(04):97-103．

［13］骆达荣，黄灏然，郭开仲．基于SVR的RAR区域经济预测模型［J］．数学的实践与认识，2013，43(19):36-42．

［14］王飞，刘红．中国民族地区当前经济发展形势分析与预测［A］//张建平，舒燕飞，王飞编著．中国民族地区经济增长预测与发展研究［M］．北京:中国经济出版社，2012:98-140．