基于多模型参数选择的雷达海杂波自适应抑制处理

李 垚，李家强，李 鹏，葛俊祥，姜庆刚

(南京信息工程大学 电子与信息工程学院，南京 210044)

0 引 言

近年来，雷达被广泛应用于国防军事、民航管制、气象、航海导航等领域。在航海及货运交通领域，船用导航雷达是船舶不可或缺的导航电子设备。当雷达检测海面目标时，其接收到的回波信号中含有大量的海杂波，这些海杂波强度通常比目标信号高出数个量级，严重干扰了有效目标的检测。因此，对海杂波特性的深入研究并通过现代雷达信号处理方法能够最大地发挥雷达在海杂波环境中的检测威力。

雷达海杂波主要包括以下四种统计分布模型，即：Rayleigh分布、Log-normal分布和Weibull分布、复合K分布[1]。如在低分辨率雷达系统中，当天线波束角较高，环境比较平稳时，一般海情的海杂波通常服从Rayleigh分布；在高分辨率雷达、低入射角的情况下，一般海情的海浪杂波通常可以用Weibull分布精确地描述[2,3]。文献[4]提出,雷达接收到的回波信号中不仅含有有效目标回波信号，同时还包括海杂波，杂波信号与风速、天线方向角、海情等诸多因素相关，所以很难判断是哪一类具体类型的海杂波，从而导致在杂波对消的过程，很难有效地抑制海杂波。针对这一问题，文献[4]应用clean算法，先对通道时域数据进行海杂波抑制，之后进行数字波束形成，得到能够正常进行目标检测的谱数据。文献[5]根据图像分割和形态学滤波原理,提出一种抑制海杂波的方法。下面首先根据已有的海杂波仿真数据，统计出其相关参数，然后提出一种基于多模型参数选择的自适应海杂波对消方法，通过对已有杂波仿真数据的概率分布曲线的拟合，并与建有的几种理想海杂波模型进行对比，找到相关参数下与之拟合情况最佳匹配的模型，最后利用这种杂波模型与回波信号进行对消，从而实现了对海杂波有效的抑制。

1 海杂波模型库

由于雷达海杂波处理难度很大，海面目标的检测将受到海水表面反射波的严重影响。所以杂波是雷达信号处理和检验的固有环境，雷达的基本任务是在杂波中进行信号处理，只有通过合理地拟合海杂波幅度分布来改善探测效果,才能了解海杂波特性[5]。目前，描述海杂波幅度分布的模型中，典型的有瑞利分布(Rayleigh)、对数正态分布(LogNormal)、韦布尔分布(Weibull)和K分布等，首先根据这些杂波类型，建立海杂波模型库。

1.1 Rayleigh分布模型

低分辨率雷达的海面杂波幅度分布一般服从Rayleigh分布，这种情况下的海浪杂波可以用Rayleigh分布描述。其概率密度为

(1)

式中，x是Rayleigh分布杂波回波的包络振幅；δ2是杂波的平均功率。Rayleigh杂波模型是实际应用中比较常见的一种模型。在δ=0.5的情况下，Rayleigh分布概率密度函数分布曲线，如图1所示。

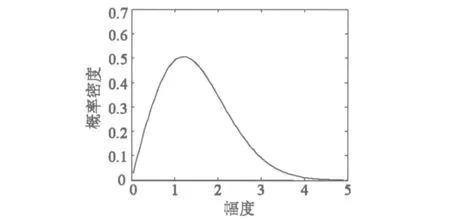
图1 Rayleigh分布概率密度函数分布曲线

1.2 Log-Normal分布模型

实验数据表明，在雷达的鉴别力提高或者在高海情下，杂波的振幅分布尾部较长，后向散射特性偏离了瑞利分布，比较符合Log-Normal分布[6]。因为其具有较长的拖尾，所以适用于低入射角，复杂地形杂波数据或者平坦区高分辨率的海杂波数据。其概率密度函数为

(2)

式中，μ是尺度参数，表示分布的均值;δ是形状参数，表明分布的偏斜度。在μ=0.5，δ2=0.2的情况下，Log-Normal分布的概率密度函数分布曲线如图2所示。

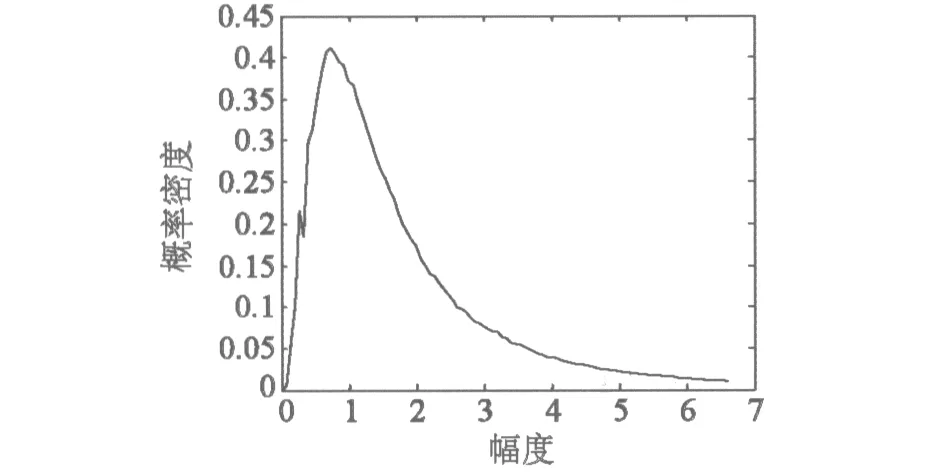
图2 Log-Normal分布的概率密度函数分布曲线

1.3 Weibull分布模型

韦布尔分布是介于瑞利分布和对数正态分布之间的一种杂波模型，能在更广的环境内精确地表示实际的杂波分布。在高分辨率雷达、低入射角的情况下，一般海情的海浪杂波通常可以用Weibull分布描述。其概率密度函数为

(3)

式中，q为尺度参数，表示分布的中位数；p为形状参数，表示分布的偏斜度。当p=2时，Weibull分布退化为Rayleigh分布。在p=3,q=1的情况下，Weibull分布的概率密度函数分布曲线如图3所示。

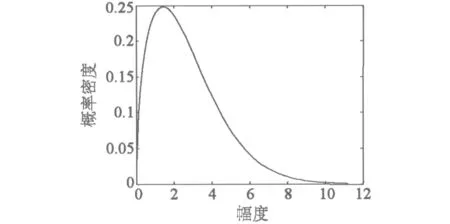
图3 Weibull分布概率密度函数分布曲线

1.4 K分布模型

K分布适用于高分辨率雷达、低入射角的情况，已经广泛的应用于地、海杂波建模，它不仅在很宽的条件范围内与杂波幅度分布很好的匹配，而且可以正确的模拟杂波脉冲间的相关特征。K分布杂波可以看作是功率服从Gamma分布的随机过程调制的复高斯过程。其概率密度函数为

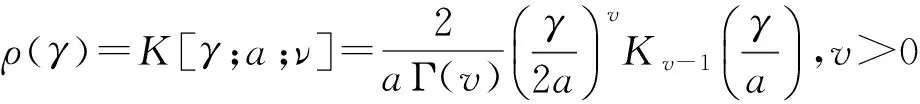
(4)

式中，Γ(·)为Gamma函数；a为尺度参数；v为形状参数;Kv-1(·)是第二类修正的v-1阶贝塞尔函数[7,8]。对于高分辨率、低入射角的雷达，形状参数的取值范围是0.1～3；当v趋于0.1时，杂波具有较长的拖尾，v趋于无穷时，杂波趋于瑞利分布。尺度参数a=2，形状参数v=0.4的情况下K分布的概率密度函数曲线图，如图4所示。

图4 K分布概率密度函数分布曲线

2 自适应海杂波对消方法

2.1 海杂波的模拟

目前常用的海杂波模拟方法主要有两种：零记忆非线性法(ZMNL,zero memory nonlinearity)和球不变随机过程法[9](SIRP,spherically invariant random process)。其中零记忆非线性法计算量小，且容易形成快速算法，具有良好的通用性}。零记忆非线性法的原理图如图5所示，输入端V为独立的白谱高斯过程，输出端为所要求的杂波序列Z,W序列是输入X经过滤波器H(w)后得到的，再经过零记忆非线性变换法将W的概率分布转换为所求Z的概率分布。下面运用零记忆非线性法产生Weibull分布的杂波序列，其原理如图6所示，其中V1,i，V1,j是两个互不相关的高斯随机序列；H(w)为线性滤波器；U1,i，U1,j是通过滤波器H(w)后的相关高斯随机序列；xi为服从Weibull分布的随机序列，Sij为相关系数。

图5 零记忆非线性法的原理图

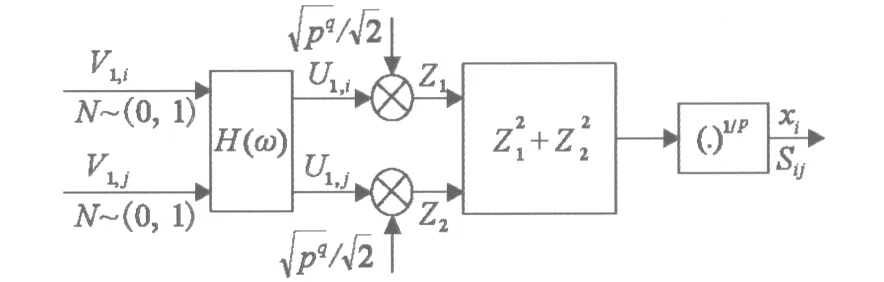
图6 Weibull分布的杂波序列原理图

仿真环境：Weibull杂波功率谱为高斯频谱，形状参数p=1.5，尺度参数q=3。仿真结果如图7、图8所示。

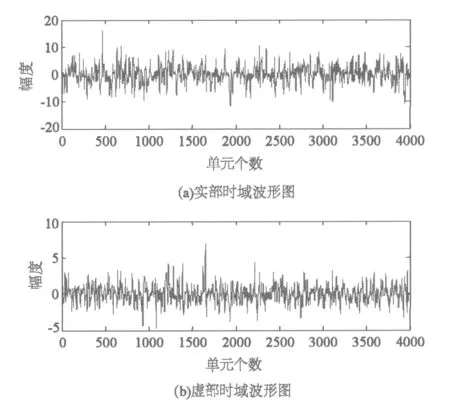
图7 Weibull杂波分布时域波形图

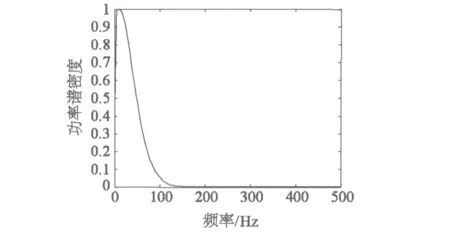
图8 Weibull杂波功率谱图

其中图7为Weibull杂波时域实部和虚部的波形图，可见没有目标的海杂波起伏毫无规律，是一随机序列。图8可以看出理想的情况下杂波的功率谱为高斯谱。

2.2 参数选择杂波模型选取与杂波对消抑制

现对一组回波仿真数据进行统计分析，在这组仿真数据中，设置目标信号在频率100 Hz和200 Hz处。通过不同参数情况下多个模型的比较，找出与之相对应的参数下的海杂波模型，对海杂波进行自适应抑制，提高目标检测能力。在对回波数据进行谱分析后可以发现目标在海杂波的干扰下很难辨别出来，所以需要找出相应的方法有效地抑制海杂波，从而提取出目标。基于多模型的海杂波自适应对消流程图,如图9所示。

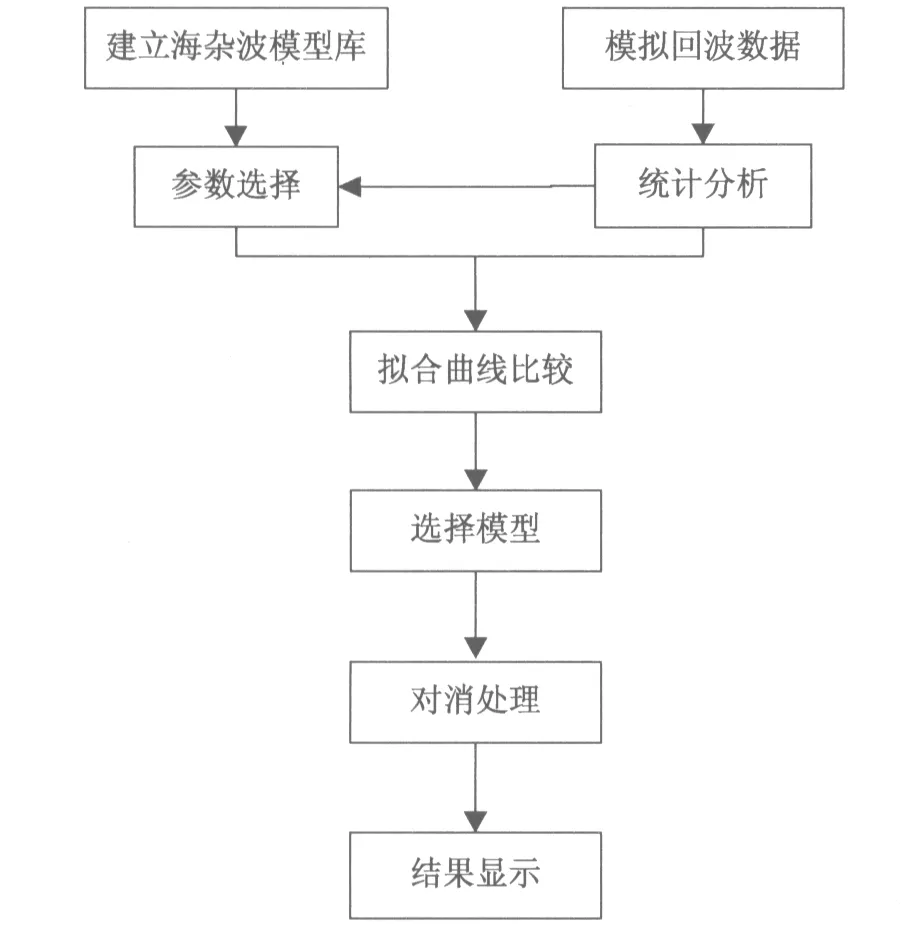
图9 基于多模型的海杂波自适应对消方法流程图

对于仿真得到的回波数据的幅度特性进行统计分析，通过对现有的海杂波模型(瑞利分布、韦布尔分布、对数正态分布和K分布)参数设置，与回波仿真数据进行比较，通过拟合检验判断出哪种参数情况下的海杂波分布模型更适合于回波信号。利用此参数情况下的海杂波模型对回波信号进行自适应对消，提取出目标信号。

具体的步骤如下：

(1)仿真得到一组回波数据，拟合出回波数据的杂波幅度分布直方图，将其与现有的海杂波模型进行拟合比较。同时拟合出它的频谱图和功率谱图，以方便与下一步的对消结果进行比较，归一化的回波信号特性如图10所示。从图10(a)、(b)中可以发现背景杂波很强，很难分辨出目标和海杂波，目标信号由于海杂波信号的存在，不容易分辨。

图10 归一化的回波信号特性

(2)将所得的回波幅度分布直方图与现有的海杂波模型幅度分布曲线进行比较，找出相关参数下与回波信号直方图相差最小的模型。实测数据概率密度与理想模型的拟合图,如图11所示。

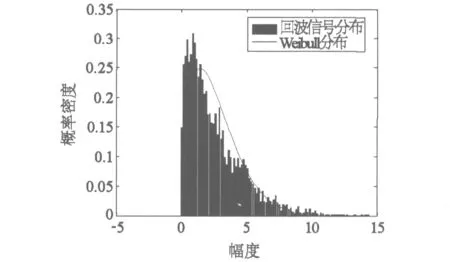
图11 实测数据概率密度与理想模型的拟合图

通过比较发现实测数据直方图与Weibull分布模型在形状参数p=3,尺度参数q=1情况下的概率密度曲线拟合情况最佳，由于杂波幅度的随机跳变，个别幅度点值分布存在差异，但不影响整体两者吻合，所以选择p=3,q=1的参数下的Weibull分布作为对消的模型。

通过以上的拟合比较，利用所选择的Weibull海杂波模型对回波数据进行海杂波对消，通过时域上回波数据减去之前选好的海杂波模型数据，从而可以有效准确地抑制杂波，提取出有用信号。归一化的自适应对消后的回波特征，如图12所示。图12(a)、 (b)箭头处可以看出通过该方法的海杂波对消后，在频率100 Hz和200 Hz处出现了两个谱峰，即目标信号。

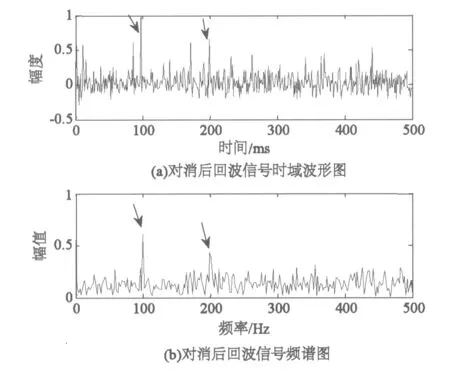
图12 归一化的自适应对消后的回波特征

通过对比对消前的图10可以明显看出图12中在相应的频率点处目标凸显出来，海杂波得到了一定的抑制，从而证实了仿真回波数据与相关参数下Weibull杂波模型拟合情况比较好。运用这种自适应海杂波比较对消的方法能够较准确的确定海杂波的类型，为下一步海杂波对消提供更精确的模型，可以明显看出此方法对消可行。

3 结 语

通过对几种海杂波模型的建立，对仿真的回波数据进行统计分析，拟合出其幅度分布直方图，并与几种海杂波的模型的幅度分布图比较，找出与回波数据拟合情况最佳的相应参数下的海杂波模型，从而利用现有的模型对仿真回波数据进行海杂波对消。通过仿真结果可以发现，此自适应方法的对消效果比较明显，从而证明此方法的有效性。该算法简单,容易用FPGA实现。

[1] 姚云萍.一种船用雷达海杂波抑制算法[J].火控雷达技术，2011,40(3):32-36.

[2] 陈闹.韦布尔分布海杂波的建模与FPGA的实现[J].火控雷达技术，2013,42(2):4-6.

[3] 杨海文.海杂波建模与实测数据分析[D].西安：西安电子科技大学，2011.

[4] 高兴斌,宗成阁,袁业术.高频地波舰载超视距雷达的海杂波对消[J].电子学报,2000,28(3):5-8.

[5] LIU JING-YAO,MENG HUA-DONG.Radar Sea Cluter Suppression and Target indication with A Spatial Tracking Filter[J].Tsing Hua Science and Technology,2010,15(2):228-234.

[6] YAN XIANG,HAMILTON MARK F.Statistical Model ofSuppression in Tissue Harmonic Imaging Coustic[J].Society of America,2011,129(3),193-208.

[7] 李云龙，基于K分布雷达海杂波建模仿真[J].制导与引信,2011,32(2):14-20.

[8] SHEN CHE-CHOU.Effect of Dual Frequency Clutter Doppler Detection[J].Ultrasonics,2011,52(2).238-243.

[9] 朱玲.地、海杂波特征建模与参数估计[D].电子科技大学，2006.

[10] 赵树杰.雷达信号处理技术[M].北京：清华大学出版社，2010：232-246.