太空系统的适应弹性研究

严晓芳，饶玉柱

(中国电子科学研究院，北京100041)

0 引 言

在太空领域的发展中，越来越多有竞争力的国家和公司不断加入对太空的探索与研究，太空环境也日益拥挤，太空系统面临的自然灾难和人为威胁日益加剧。因此，提高太空系统的适应能力、生存能力尤为迫切。

对于一个系统而言，其适应弹性研究就是针对其现在或将来可能遇到的各种各样的威胁，包含导致丧失体系/系统能力的任何环境或人为活动。弄清威胁所在是改进一个系统适应能力、生存能力的基础。

1 太空环境面临的威胁

在对威胁的分析中，通常将威胁视为一起事件。在该事件没有发生之前，系统能正常发挥各项功能，但当事件发生后，如果事件威胁超过了系统的预定承受能力，系统的部分功能开始丧失。随着时间推移，有可能进一步丧失系统的主要功能甚至全部功能。当然，事件的发生过程和系统全部能力损失也可能是瞬间发生的，对这种状态的判定也要视具体系统的功用而定。

一起事件对目标系统造成功能损伤后，可以把此起事件和系统结合后的状态称为一个威胁场景。单个威胁场景往往只存在于理论分析之中，多个威胁场景的组合才是实际面临的情况。

根据威胁的来源，可以将其分为两类：不利条件和敌对行动。不利条件指的是由自然环境产生的威胁，如天气条件、地震等各类自然灾难；太空中的宇宙射线、陨石等造成的威胁。敌对行动指的是由对手造成的威胁，如针对实体系统本身的各类物理攻击、各种辐射攻击(如射频或光学攻击)、干扰、欺骗，以及赛博行为等造成的威胁。

典型的威胁情形列举如下。

a)不利条件

(1)近地物体和彗星等星体；

(2)太空天气时间和宇宙射线；

(3)太空碎片；

(4)地球上的自然灾难。

b)敌对行动

(1)反卫星武器(同轨道或导弹)；

(2)外太空核爆；

(3)射频武器(干扰、高能量射频伤害系统)；

(4)赛博攻击(信号窃听，非授权命令、黑客)；

(5)在自然环境蓄意引发变故；

(6)邪恶的破坏或监视行动；

(7)对地面设施进行物理攻击(地面站、发射站、通信网络、电力网、人员等)；

(8)激光武器(炫目级或伤害级)；

(9)带电的或中性粒子流；

(10)升级太空攻击能力(可跟踪更小的目标，更迅速的变轨响应能力和更精确的跟踪能力，对敌对卫星的配置、操作状态以及现有活动的评估能力，对太空天气事件的及时告警能力等)；

(11)改进的地上设施(多样化的指挥和控制信息，通过地上通信设备实现互联，加强站点物理位置的安全性，使用更高级的固态定向天线等)；

(12)伪装、隐藏和欺骗。

美国尤其关注“敌对行动”这类的威胁。自然界的不利条件往往可以预料，即使是意料之外的事件，由于其发生概率很小，因此不值得预付过多的资源和精力加以应对。而敌手的行为难以预期，采取的手段也在不断更新，攻击的对象也不确定，因此要切实增强太空系统的适应能力和生存能力就应重点关注“敌对行动”这类威胁。

美国国防部很早就在探索保证太空系统在困境中正常工作的方法，而且早在2011年6月，美国波音公司和SURREY卫星科技有限公司就开始探索太空系统适应弹性的评估方法，到2013年8月波音公司已经探索出对比和评估不同类型太空架构的方法，包括系统崩溃对适应弹性的影响等，但尚未完全应用到生产制造中去。

2 系统的适应弹性

2.1 适应弹性的定义

适应弹性是指系统具备保证实现各项功能和任务成功的能力，即使在敌对行动或是不利条件下也能保证任务成功[1]。这种功能性的任务保证必须覆盖所有可预期的场景、环境及威胁。适应弹性关注如何保持、加强和保护各项系统能力。按从顶层到低层的角度，可以将适应弹性分为企业级、任务级、功能级等层级，这种分级方式既可针对不同领域的系统，也可针对同一个领域的系统功能。

显然，对太空系统适应弹性的关注点为：在包括敌对行动和不利条件在内的各类威胁下，保证一个太空系统在军事、情报等方面的任务执行能力维持在一个必要的水平之上[2]。

按照时间顺序，一个系统在遇到威胁后一般会经历四个过程，即在外界威胁下正常工作、系统部分性能丧失、主要功能丧失(系统崩溃)、系统恢复正常。适应弹性通常可分为避免性、健壮性、恢复性和重建性[2]。适应弹性随时间的演变过程如图1、2所示。

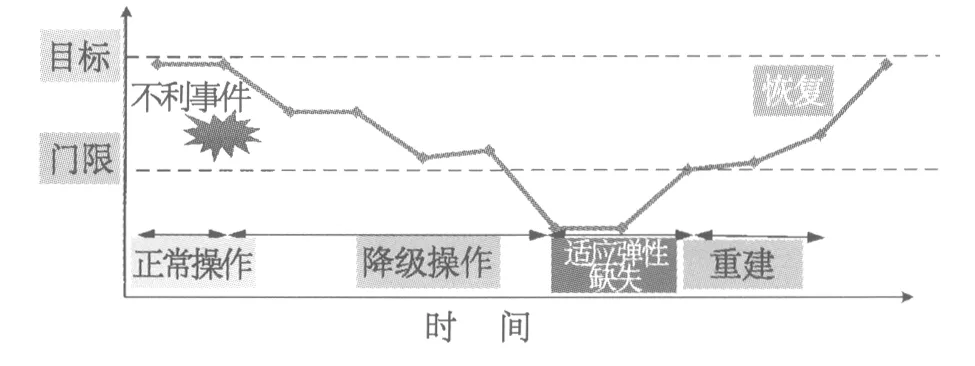
图1 适应弹性的演变过程

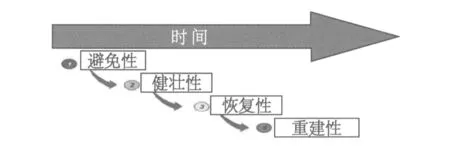
图2 适应弹性属性的时序关系

避免性：针对潜在对手的反制措施，采用主动的或对抗性的防御措施来减少敌对行为或不利条件发生的可能性和后果。该项能力主要在威胁事件发生之前发挥作用。

健壮性：是增强生存性、抵制功能降级的系统属性和系统设计特征。该项能力主要适用于威胁事件发生之后，出现部分系统性能丧失，并一直持续到主要功能丧失为止。

恢复性：在一个特定任务、操作或意外事故发生的情况下，进行规划和操作以弥补丧失的功能，从而使系统能力能够达到一个可以接受的水平。该项能力主要发生在系统主要功能丧失之后，由于各种原因，系统能力开始恢复，一直持续到该系统的主要功能甚至全部功能恢复正常为止。

重建性：在面对全部任务、操作或意外事故情况下，开展项目执行和空间支持操作来重建整个系统的能力。该项能力主要发生于系统的主要功能开始恢复直至全部能力恢复正常的这段时间内。

要保持和增强系统的适应弹性，可从以上四部分分别着力或着重从某一部分着力，若一个部分能够做到完美，就可以保证整个系统的适应弹性趋于完美。这里所说的适应弹性的完美是在限定时间内实现的。而以上的划分方式将适应弹性对应的限定时间分为了四段，任意一段只要做到完美就可以使系统保持或立即恢复正常状态。保持和增强适应弹性的典型做法，如图3所示。

图3 保持适应弹性的方法

2.2 系统适应弹性的评估过程

由前面的分析可知，威胁与适应弹性息息相关，针对一个系统适应弹性的评估必须从具体的威胁场景开始。评估过程如下。

(1)首先确定一个系统处于稳定工作状态，它已具备了避免相关威胁的能力，这体现在对威胁的预测分析、探测识别上，一旦遇到不利事件就启动威胁避免措施。如果成功，就可以保持稳定工作状态(适应弹性保持)。

(2)如果避免威胁失败，但系统能力并没有失效，仍然可以稳定工作到任务结束，则可以认为系统具有完美的健壮性；若是仅仅系统部分能力失效，但仍然可以保持主要功能并工作到任务结束，可以认为该系统只是处于功能降级状态，并没有危及到主要功能的发挥，此时该系统仍可以正常工作(适应弹性保持)。

(3)如果系统功能降级后，继续丧失功能，直至主要功能失效，则可认为此时系统的适应弹性缺失(不能正常工作)。

(4)在系统的适应弹性缺失后，采取措施致使系统的主要功能甚至全部功能恢复，则可认定此时系统的适应弹性得到恢复(返回稳定工作状态)，具体评估过程如图4所示。

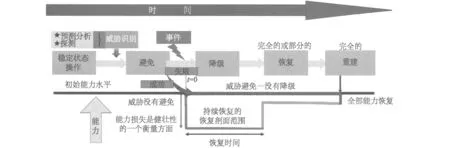
图4 适应弹性的评估过程

3 适应弹性计算

3.1 适应弹性计算公式

根据上文中对适应弹性测评过程的分析，可以得到适应弹性的计算公式[3]。即：

R=RAV+(1-RAV)RRO+
(1-RAV)(1-RRO)RRV+
(1-RAV)(1-RRO)(1-RRV)RRC

(1)

式中，各参数说明如下。

R(Resilience)适应弹性是系统面对威胁的适应概率；该值可以定量表现系统面对威胁全过程的适应能力；适应弹性是四个属性的函数。

RAV(Avoidance)避免性的概率，它是针对威胁被完全避免的可能性量度。

RRO(Robustness)健壮性的概率，体现了系统能力保存的能力，它是对为避免系统失效而保留必要系统能力的量度。

RRV(Recovery)恢复性的概率，体现了系统恢复能力以及恢复时间，它是针对失效能力能够被恢复的程度以及特定任务恢复时间的量度。

RRC(Reconstitution)重建性的概率，体现了系统在面临外界威胁时的应对能力，重建遭到破坏后的系统主要能力，保证系统稳定运行。

从式(1)中可以得到，RAV，RRO，RRV，RRC只要有一项等于1，就可以使R的值为1。

等式的对称性进一步表明：为了得到系统的适应弹性，可以使用多个方法，且每个方法都有同样的影响。这为提高系统的适应弹性提供了理论支持，我们可以根据不同情况，重点提升适应弹性中的一个属性，使其达到完美状态，这样就可以使适应弹性达到完美状态；也可以提升适应弹性中的各个属性，使系统具有较好的综合适应弹性。

根据实际威胁情形的不同，以下将逐步介绍单个威胁、多个不相关威胁、多个相关威胁、全部威胁场景下适应弹性的计算公式和太空系统的计算案例，指出保持卫星等太空系统适应弹性的关键方法。

3.2 单个威胁情况下适应弹性计算案例

对于某种具有特定能力的卫星系统，假定其对某种威胁具有以下能力。

Avoidance(RAV):可以避免60%的威胁，即RAV=0.6；

Robustness(RRO):如果威胁没有避免，系统将保留50%的能力，即RRO=0.5；

Recovery(RRV):在一个可以接受的期限内，失效的卫星系统能力中有25%能够被恢复，即RRV=0.25；

Reconstitution(RRC):只能通过发射一枚替代性卫星才能恢复全部能力，将会用相当多的时间，可设为10%，RRC=0.1；

此时该卫星系统面对该威胁下的适应弹性为：

R=0.6+(1-0.6)*0.5+

(1-0.6)(1-0.5)*0.25+

(1-0.6)(1-0.5)(1-0.25)*0.1

=0.865

该适应弹性数值表示，在威胁情况下，能够用概率数值定量表示保持卫星系统功能正常的预期值。

3.3 多个不相关威胁情况下，系统适应弹性计算案例

在一个系统面对不同类别、不相关威胁的情况下，可以分别计算不同威胁造成的适应弹性数值，对各个适应弹性数值进行比较，最小值对应的威胁即为系统的关键性威胁。

以各种不相关威胁同时作用于某太空系统的案例，系统的最小适应弹性见表1。系统的关键性威胁指的是单个威胁就可以导致最大系统性能的损失。上表橙色框对应的威胁导致系统适应弹性最小，为0.8。因此，此时要增加该系统的适应弹性就必须从改善系统对“物理攻击”威胁的各项因素角度出发，只要实现该项的任何子项(避免性概率RAV，健壮性概率RRO，恢复性概率RRV，重建性概率RRC)为1，就可迅速提高整个太空系统的适应弹性。

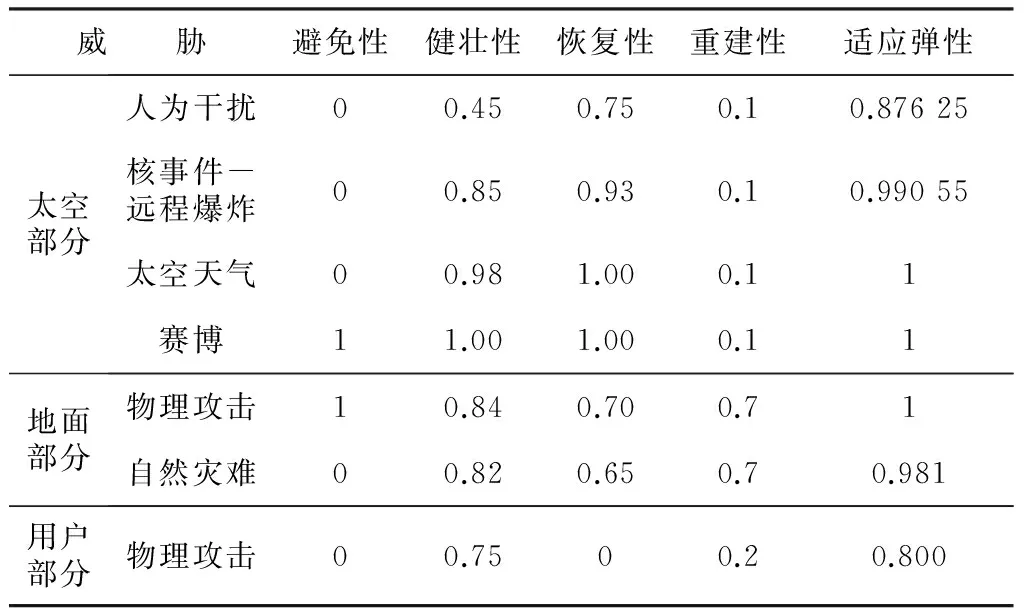
表1 关键性威胁对应的适应弹性计算案例

3.4 多个相关联威胁情况下系统的累积适应弹性分析案例

对于包括多个、相关威胁的威胁场景，需要对整个系统的适应弹性进行计算。在整个系统能力上，每个额外威胁都可能产生累积作用，从而导致系统功能的减少。必须要仔细评估系统面临每个威胁时的健壮性，并防止重复计算的发生。

此时计算系统累积适应弹性的步骤如下。

(1)按照式(1)计算出各个单威胁下的适应弹性Rn(n=1、2、…)；

(2)按照式(2)计算出系统的累积适应弹性，

(2)

式中，N为威胁的总数；Rs为累积的系统适应弹性(N个威胁);R1为第1个威胁的适应弹性；Rn为第n个威胁的适应弹性。

三种相关威胁同时作用于某太空系统的案例，见表2。给出了来自太空和地面的三个威胁共同作用下的累积适应Rs。Rs是以上三个威胁下系统的最终适应弹性计算结果，在全系统的计算中，只要使用Rs就可以描述这三个相关威胁对系统的总体影响了。

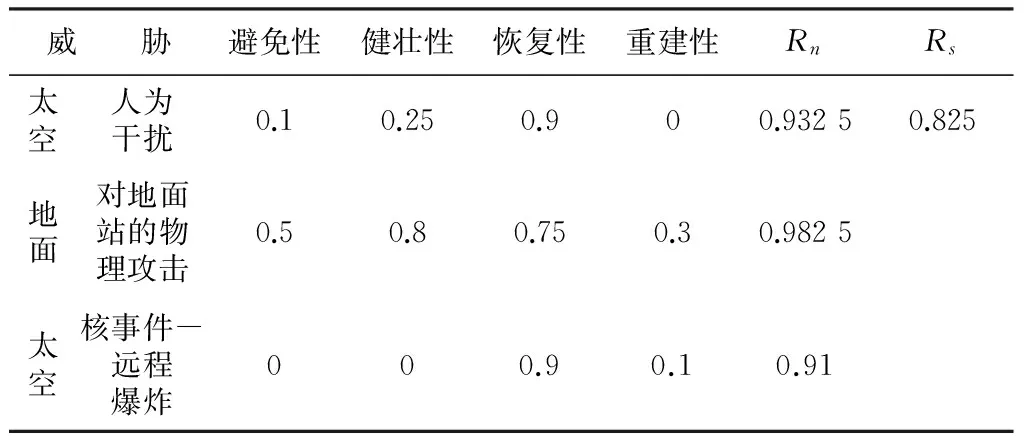
表2 多个相关联威胁情况对应的累积适应弹性案例

3.5 全部已知发生概率并且不相关威胁情况下，全系统累积适应弹性分析案例

若能够运用统计等方法，得知系统的全部威胁(各威胁为独立事件)及各个威胁场景的发生概率，则可以根据各个威胁场景发生的概率，对全系统的累积适应弹性进行计算。该方法只是概率性的，可以通过为所有威胁场景的适应弹性创造一个“期望值”来实现对多个威胁下累积性适应弹性计算概念的方法拓展，但这并不是完全真实的场景，只是对真实世界场景使用概率统计方法所做的一种定量描述。

全系统累积适应弹性的计算为

(3)

式中，RFS为全系统累积适应弹性(N为威胁场景总数)；Rn为第n个威胁场景的适应弹性；Pn为第n个威胁场景发生的概率。

以各种已知发生概率并且不相关威胁同时作用于某太空系统的案例，给出了来自太空和地面的三个威胁共同作用下的系统累积适应弹性见表3。

表3 全系统累积适应弹性计算案例

表3以各种发生概率不同的不相关威胁同时作用于某太空系统的案例，给出了系统的最小适应弹性RFS。一般来讲，威胁场景发生概率Pn往往来自试验和实际观察统计结果，通过比较全系统中各个分系统而得，但引入Pn更贴近实际情形，RFS的计算结果更能体现系统在各种威胁条件下的正常工作能力。

3.6 计算结论

通过以上各种假设条件下的计算，可以得到这样一种结论：存在多种方法来获得一个更具适应性和生存能力的系统。因此，以系统适应弹性的方法作指导，可以比较各种系统架构的优劣，使用各种措施改进系统架构，使其具有更好的适应弹性，改进现有系统构建模型；建立数据库存储更多的系统适应弹性信息；保证在适应弹性上对系统进行持续评估,这些都有助于提升系统的适应弹性。

4 结 语

提出适应弹性的概念并进行系统测评，是非常有意义的事情。具体表现有：

第一，通过建立系统适应弹性模型，对系统的避免性概率、健壮性概率、恢复性概率、重建性概率及威胁概率进行分析，可以快速发现系统的薄弱环节，有针对性地加以改进，从而有效提高现有系统的适应弹性；

第二，不同系统之间有了明确的评判标准，这是方案论证时评价不同系统方案优劣的依据之一；

第三，根据适应弹性四个阶段的不同影响因素，可以选择具有不同适应弹性优点的系统(如A的避免性优，B的健壮性优)进行组合，从而使组合后的新系统具有更强的适应性和生存能力。

第四，在其他领域推广系统适应弹性的评价方法，提高该领域的某些系统的适应性和生存能力。

[1] BURCH R.Measures of Resilience for Space Systems Space-Forum-Boeing[Z].

[2] JOHNSON,C W.The Application of Resilience Engineering to Human Space Flight[Z].

[3] IAWG-REGLAP，ThinkSpace report NairobiJan 2013.

[4] Satellite Navigation & Space Weather:Understanding the Vulnerability &Building ResilienceAmerican Meteorological Society Policy Workshop Report March 2011.