改进同伦分析方法及非线性热传导问题的同伦解

韩元春, 那仁满都拉

(内蒙古民族大学 物理与电子信息学院, 内蒙古 通辽 028043)

实际上,工程中遇到的大量的热传导问题应该用非线性热传导方程来描述.自然界中的其他现象,如扩散、渗流等都与热传导现象有共性之处,因此也可用类似的非线性方程来描述.因此,非线性热传导方程的研究一直是数学和物理学家关注的热点问题.然而,由于非线性方程的复杂性,大多数方程很难求得精确解析解,只能用数值方法或近似解析方法求得近似解.Lyapunov人工小参数法、摄动方法、δ展开法和Adomian分解法等传统近似方法,虽然能够成功地解决许多非线性问题[1],但这些方法给出级数解的收敛区域和收敛速度都是确定的,不能简便地控制和调节级数解的收敛区域和收敛速度.针对这些不足,廖世俊[2]发展传统的同伦方法,提出同伦分析方法.该方法的优点是适合于求解强非线性问题、无需小参数假设条件、可自由选取基函数而更有效地表达解、所得级数解的收敛区域和速度可由一个辅助参数来调节和控制.文献[3-7]中证实了该方法的有效性.文献[8]改进了文献[2]提出的同伦分析方法,得到带有2个辅助参数的改进同伦分析方法.该方法可提供2个辅助参数来调节和控制所得级数解的收敛区域和速度,从而实质性地改善同伦分析方法所得级数解的收敛区域和速度,使其更有效地求解和分析复杂非线性问题.

一般热传导问题的一维控制方程[9]为

(1)

其中,u表示温度,k(u)为传热系数,f(u)是热源产生的热量,两者都是温度的函数.当k(u)和f(u)为温度的不同函数时,方程(1)表示不同的非线性热传导方程.当k(u) = 2u,f(u) =β(u-u2)时,方程(1)表示文献[10]中研究的非线性热传导方程

(2)

当k(u)=α,f(u)=β(u-u3)时,方程(1)就表示文献[11]中研究过的非线性热传导方程

(3)

在方程(2)和(3)中,α和β是任意常数.

本文先介绍改进的同伦分析方法,并运用该方法,将研究非线性热传导方程(2)和(3)在初始条件(4)和(5)下的传热问题,给出2种非线性初值问题的同伦解,并分别与该问题的精确解进行比较分析

(4)

(5)

1 改进同伦分析方法简介

对于原同伦分析方法,许多文献做了介绍和应用[1-6].因此,本节介绍改进同伦分析方法时,只介绍对原方法的改进部分,其余部分不再阐述.文献[8]主要在2个方面对原同伦分析方法进行了改进.首先对原同伦分析方法的零阶形变方程进行改进,构造新的零阶形变方程为

[1-gp+(g-1)p2]{L[φ(x,t;p)-

u0(x,t)]}=phN[φ(x,t;p)],

(6)

其中h(h≠0)和g都是辅助参数.由于方程(6)包含2个辅助参数h和g,第二个辅助参数g对开始系统到目标系统之间的同伦增添了一个新的自由度,因此能够更有效地调节和控制所得级数解的收敛区域和速度.当第二辅助参数g=1时,零阶形变方程(6)就变成廖世俊[2]提出的原同伦分析方法的零阶形变方程.因此,原同伦分析方法的零阶形变方程可看作是方程(6)的一种特殊情况.其次对原同伦分析方法的高阶形变方程改进为

L[um(x,t)-χmgum-1(x,t)+

(7)

其中

(8)

很显然,当g=1时,高阶形变方程(7)就变成原同伦分析方法的高阶形变方程.对方程(7)两边作用逆算符L-1可得

(9)

这样,由(9)式和初始猜测解,可得原方程的任意阶级数解.

2 初值问题的同伦解

2.1方程(2)满足初始条件(4)的同伦解依照改进同伦分析方法的思想,首先选择如下初始猜测解

(10)

以及辅助线性算符

这里c为初始条件确定的积分常数.另外,根据方程(2),定义非线性算符为

βφ(x,t;p)+βφ(x,t;p)2,

(12)

这样,可构造如下零阶形变方程

[1-gp+(g-1)p2]{L[φ(x,t;p)-u0(x,t)]}=

phN[φ(x,t;p)].

(13)

当p=0,p=1时,显然有φ(x,t;0)=u0(x,t),φ(x,t;1)=u(x,t).由零阶形变方程(13),可得到如下m阶形变方程

L[um(x,t)-χmgum-1(x,t)+

(14)

以及所满足的初始条件um(x,0)=0.上式中

(15)

m阶形变方程(14),对于m≥1的解为

um(x,t)=χmgum-1(x,t)-

(16)

这样,由(10)和(16)式可以计算出u1(x,t),u2(x,t),u3(x,t),…,从而可得到原方程任意阶级数解

(17)

这里利用数学软件Maple,当β=1时计算出了前10项(由于表达式太长这里已忽略),并得到了如下10阶级数解

(18)

图1 v=μt(0,0)等高线图Fig. 1 Contour map of V=μt(0,0)

图2 级数解(18)(实线)与精确解(圆圈)的比较:Fig. 2 Series solution (18)(real line) comparison with the exact solution(circle line)

图3 原同伦分析方法和改进同伦分析方法给出解(实线)与精确解(圆圈)的比较Fig. 3 The comparision of the solution(real line) by using original homotopy analysis method and improved one with the exact solution(circle line)

2.2方程(3)满足初始条件(5)的同伦解同样,初始猜测解和辅助线性算符选为

这里c为初始条件确定的积分常数.另外,还定义非线性算符

这样,可构造如下零阶形变方程

[1-gp+(g-1)p2]{L[φ(x,t;p)-u0(x,t)]}=

phN[φ(x,t;p)].

(22)

由零阶形变方程(22),可得到如下m阶形变方程

L[um(x,t)-χmgum-1(x,t)+

(23)

以及所满足的初始条件um(x,0)=0.在(23)式中

(24)

m阶形变方程(23),对于m≥1的解为

um(x,t)=χmgum-1(x,t)-

(25)

这样,当α=2,β=0.2时,用数学软件Maple计算出前10项(这里已忽略),进而得到了如下级数解

(26)

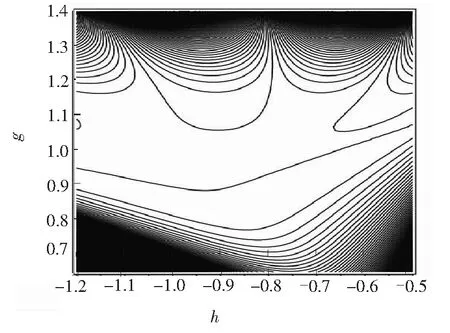
图4 W=ut(0,0)之等高线图Fig. 4 Contour map of W=ut(0,0)

图5 级数解(26)(实线)与精确解(圆圈)的比较Fig. 5 Series solution (26)(real line) compared with the exact solution(circle line)

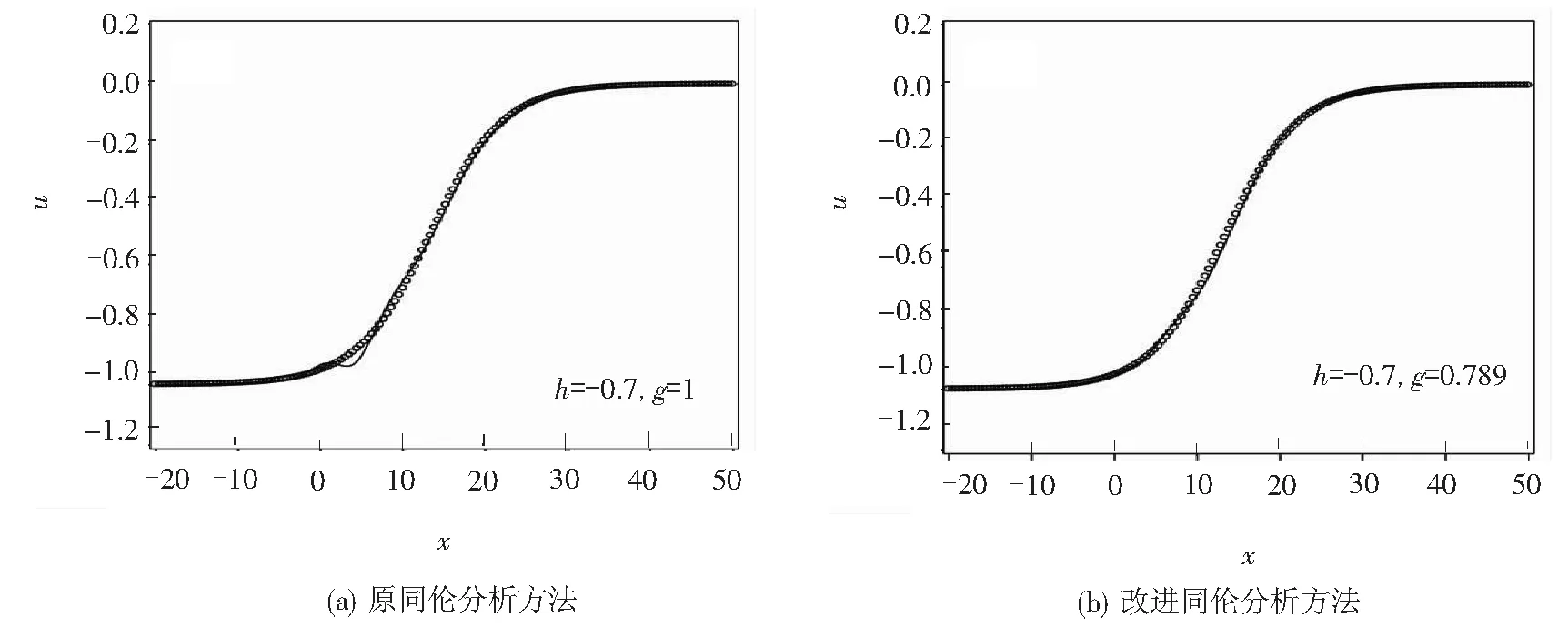
图6 原同伦分析方法和改进同伦分析方法给出解(实线)与精确解(圆圈)比较Fig. 6 The comparision of the solutions(real line) by using original homotopy analysis method and improved one with the exact solution(circle line)

3 结语

本文首先介绍了一种改进同伦分析方法,然后用该方法研究非线性热传导方程,得到不同初始条件下的2种同伦解.把所得的2种同伦解与该问题的精确解分别进行比较后发现了两者的高度吻合性.这表明利用改进同伦分析方法可以获得非线性方程的高精度近似解.另外,把改进同伦分析方法给出的解和原同伦分析方法给出的解分别与精确解进行比较,结果发现由于改进同伦分析方法中有2个辅助参数来调节和控制所得级数解的收敛区域和速度,所以改进同伦分析方法给出的解能够更快、更好地逼近真实解.可见,改进同伦分析方法对复杂非线性问题的研究有它的独特优点.非线性热传导问题的研究具有重要的理论意义和实际应用价值[9-12],而本文介绍的方法和所得结果将有助于深入分析这类非线性问题.

致谢内蒙古民族大学科研创新团队建设计划资助项目对本文给予了资助,谨致谢意.

[1] Hinch E J. Perturbation Methods [M]. London:Cambridge University Press,1991.

[2] 廖世俊. 超越摄动-同伦分析方法导论[M]. 北京:科学出版社,2006.

[3] Liao S J. On the homotopy analysis method for nonlinear problems[J]. Appl Math Comput,2004,147:499-513.

[4] 石玉仁,许新建,吴枝喜,等. 同伦分析法在求解非线性演化方程中的应用[J]. 物理学报,2006,55:1555-1560.

[5] 吴钦宽. 一类燃烧模型的同伦分析解法[J]. 物理学报,2008,57:2654-2657.

[6] 那仁满都拉,韩元春. 非均匀圆柱壳中非线性波传播模型的同伦分析解法[J]. 物理学报,2010,59(5):37-42.

[7] Rashidi M M, Domairry G , Dinarvand S. Approximate solutions for the Burger and regularized long wave equations by means of the homotopy analysis method[J]. Communications in Nonlinear Science and Numerical Simulation,2009,14:708-717.

[8] Wu Y Y, Cheung K F. Homotopy solution for nonlinear differential equations in wave propagation problems[J]. Wave Motion,2009,46(1):1-14.

[9] Sachdev P L. Nonlinear Diffusive Waves[M]. London:Cambridge University Press,1987.

[10] Wilhelmsson H. Explosive instabilities of reaction-diffusion equation[J]. Phys Rev,1987,A36:965-966.

[11] Constantin P, Foias C, Nicolaenko B, et al. Integral Manifolds and Intertial Manifolds for Disspative Partial Equations[M]. New York:Springer-Verlag,1989.

[12] 许丽萍,张春阳,米小红. 一类非线性热传导方程的线性化解法[J]. 四川师范大学学报:自然科学版,2008,31(4):393-396.