关于有杆抽油系统模型的构建
杨星星
宿州学院数学与统计学院,安徽宿州,234000
目前,开采原油广泛使用的是有杆抽油系统。电机旋转运动转化为抽油杆上下往返周期运动,带动设置在杆下端的泵的两个阀相继开闭,从而将地下上千米深处蕴藏的原油抽到地面上来。
通过悬点示功图可以初步诊断油井的工作状况,如产量、气体影响、阀门漏液、沙堵等。要精确诊断油井的工作状况,最好采用泵功图。然而,泵在地下深处,使用仪器测试其示功数据实现困难大、成本高。因此,通过数学建模把悬点示功图转化为杆上任意点的示功图并最终确定泵功图,以准确诊断油井的工作状况,是一个很有价值的研究课题。
电机旋转运动通过四连杆结构转变为抽油杆的垂直运动[1]。经分析四连杆机构简图,发现求解悬点的运动规律可以转化为求解驴头点的运动规律。但经过计算,由于各条线段间的几何关系,电机旋转不可能实现圆周运动,这里假设各个连接点处有间隙量,可保证电机的圆周运动。因此,可在不同的假设条件下,通过以下三种方法进行求解:(1)将驴头B点的运动规律简化为简谐运动,此模型比较简单,但结果较为粗略,只能用于定性分析及近似计算。(2)若把驴头B点绕游梁支点的弧线运动近似地看作直线运动[2],则驴头B点的运动模型简化为曲柄滑块机构运动。(3)通过几何分析精确求出B点运动规律的表达式,最后将驴头点的运动规律转化为悬点的运动规律:位移函数、速度函数、加速度函数。
1 模型假设
(1)抽油杆在垂直井中工作,抽油杆不与油管发生摩擦或摩擦载荷不计;(2)油管内充满液体,且液体密度均匀;(3)电机旋转运动为匀速运动,且可实现全周旋转;(4)抽油机的油管是锚定的,不考虑抽油管的长度变化;(5)抽油杆柱截面为圆形;(6)将原油粘度、原油密度、油压视为常数,不随压力而变化;(7)忽略游动阀和固定阀漏失、游动阀关闭迟缓和上、下碰泵等情况。
2 符号说明
SE表示悬点位移;vE表示悬点速度;aE表示悬点加速度;φ表示曲柄转角,rad;w表示曲柄角速度,rad/s;u(x,t)表示抽油杆在x断面不同时间t的位移函数,m;E表示抽油杆的弹性模量,N/m3;Ar表示抽油杆截面积,m2;Dt、Dr分别表示油管内径、抽油杆直径,mm;Q表示油井的实际产量,m3/d;ηv表示混合物的体积系数,m3/m3;SPE表示柱塞有效冲程,m;NS表示抽油机的冲次,min-1;r表示混合液密度,kg/m3;p表示井下压力,M/Pa;θ表示井下温度,θ=1.8t+32,F;Qp表示理论产量,t/d;Q表示泵功图法计算的产量,t/d;A表示泵功图面积,cm2;Ap表示理论泵功图面积,cm2;μ表示油管内液体的动力粘度,Pa·s;c表示粘滞阻尼系数,s-1;L表示抽油杆的长度,m;D表示泵径,mm;S表示冲程,m;n表示冲次,min-1;α表示应力波在抽油杆中的传播速度,一般取4 960 m/s。
3 曲率模型的建立
取连续曲线上任意一点,将其曲率K定义为夹角α对弧度S的变化率,并等于曲率半径R的倒数,如下所示:
(1)
由于泵功图曲线由一系列离散点组成,其解析函数无法得到,故无法由式(1)直接求得泵功图上任一点的曲率。
本文将相邻三点圆弧近似为连续曲线来求泵功图各离散点的曲率K,即利用泵功图上任意离散点Xi(xi,yi)及其前一离散点Xi-1(xi-1,yi-1)和后一离散点Xi+1(xi+1,yi+1)三点之间的几何关系,计算出点Xi(xi,yi)的曲率,如图1所示。
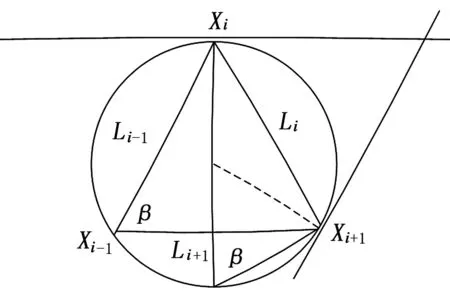
图1 离散点曲率求解模型
由三角几何关系容易得出:
(2)
将Ki=1/R进行整理,可得到:
(3)
式中,R为点Xi到点Xi+1圆弧段的曲率半径,m;α为点Xi到点Xi+1圆弧段的夹角,rad;Li-1为点Xi-1和点Xi之间的线段长度,m;Li为点Xi和点Xi+1之间的线段长度,m;Li+1为点Xi+1和点Xi-1之间的线段长度,m;SΔ为任意三角形ΔXi-1XiXi+1的面积,m2。
将式(2)代入式(3)可得:
(4)
式(4)即为求某一离散点曲率的数学模型,其中任意三角形的面积SΔ由海伦[3]公式求得:
(5)
4 模型的建立与求解
有杆抽油系统是以游梁支点和曲柄中心的连线作固定杆,以曲柄、连杆和游梁后臂为三个活动杆所构成的四连杆机构[4]。
4.1 简谐运动模型
若抽油机的r/l→0及r/b→0,即认为曲柄半径r比连杆长度l和游梁后臂b小得多,以至它与l和b的比值可以忽略。此时,可将桥梁和连接点B点的运动简化为简谐运动,即认为B点的运动规律和D点作圆周运动时在垂直中心线上的投影(C点)的运动规律相同,则B点经过t时间(曲柄转角φ)时的位移SB为:
SB=r(1-cosφ)=r(1-coswt)
(1)
因此,运动模型的悬点位移SE、速度vE、加速度αE分别为:
(2)
(3)
(4)
简化为简谐运动的模型比较简单,但结果较为粗略,只能用于定性分析及近似计算。
4.2 曲柄滑块模型
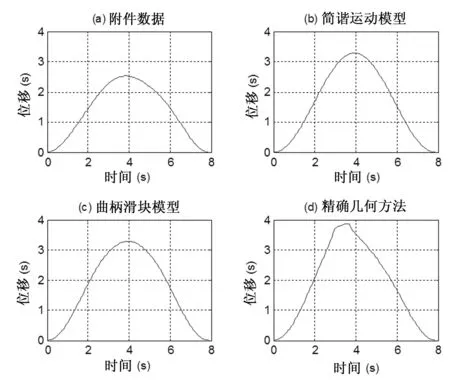
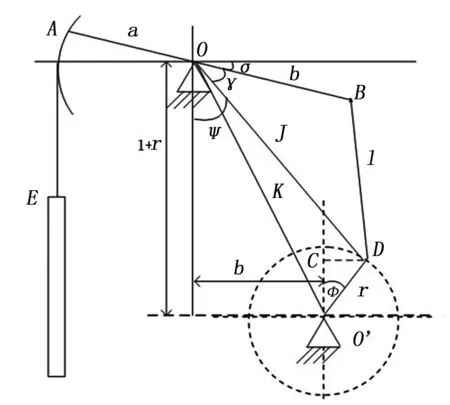
实际抽油机的r/l值是不可忽略的,特别是冲程长度较大时,忽略后会引起很大误差。为此,取r/l的值为有限值,当抽油机的0 图2 曲柄滑块模型 图2中,下死点(φ=0°)B点在B′位置,上死点(φ=180°)B点在B″位置,则B′B″=2r。因此B点经过t时间(曲柄转角φ)时的位移为: SB=B′B=B′O′-BO′ =l+r-(BC+CO′) =l+r-(lcosψ+rcosφ) (5) (6) 因此,运动模型的悬点位移SE、速度vE、加速度αE分别为: (7) (8) (9) 以下给出抽油机悬点运动规律的精确解。 图3 精确方法示意图 如图3所示,任意时刻游梁与水平线之间的夹角σ为: (10) (11) (12) (13) 游梁摆动时的最小夹角即t=0时刻AB水平时,此时σmin=0。 任意时刻游梁的角位移Δσ为: Δσ=σ-σmin (14) 因此,运动模型的悬点位移SE、速度vE、加速度αE分别为: SE=SA=αΔσ (15) (16) (17) 考虑到抽油机四连杆机构存在如下几何关系[5]: (18) 可得悬点运动速度和加速度的另一种较为简便的表达式: (19) (20) 对简谐运动、曲柄滑块机构以及精确求解时悬点位移函数进行仿真分析,如图4所示。 图4 位移函数曲线 悬点E的位移函数如图4所示,图4(a)是根据已知材料中悬点位移数据描点画出的位移函数曲线,图4(b)、图4(c)和图4(d)是根据三种不同的模型得到的位移函数曲线。图4(b)是基于简谐运动模型的,图4(c)是基于曲柄滑块模型的,图4(d)是根据精确的几何计算模型得到的。通过比较,不难发现,用三种模型计算得到的位移曲线与根据实测数据绘制出的位移曲线是相近的,尽管同一时间下的数值不同,但其变化趋势是类似的,从而验证了模型的有效性。由于每种计算模型都是基于一定假设的,因此会与实测数据有少许偏差。 [1]张琪.基于泵功图分析的有杆泵井故障诊断系统[D].大连:大连理工大学研究生院,2011:24-26 [2]岳广韬.抽油机井地面示功图量油技术研究[D].北京:中国石油大学石油工程学院,2011:11-20 [3]董世民,崔晓华.计算抽油泵充满系数的新方法[J].石油机械,2002,30(1):37-39 [4]吴伟,陈国定,何焱,基于人工神经网络和灰度矩阵的泵功图诊断[J].西安石油大学学报:自然科学版,2007,22(3):31-33 [5]爨瑾,基于灰色理论的抽油井泵功图诊断技术研究[J].微电子学与计算机,2005,22(3):7-13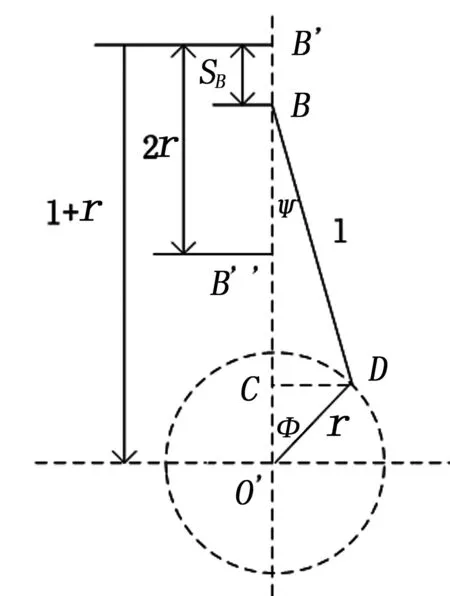

4.3 精确方法

4.4 仿真分析