混联系统的可靠性蒙特卡诺模拟及其EB估计

张民悦，岳 磊

(兰州理工大学 理学院，甘肃 兰州 730050)

现代各类电子产品和机械系统复杂繁琐，种类多样。混联系统的可靠性分析是系统可靠性研究的重要内容之一。目前该系统已被用于机械系统、电子元件系统以及质量与控制系统等工程领域。关于混联系统的可靠性分析，已有了较为详细的讨论。曹晋华[1]假定元件的失效率为常量和变量时，分别给出了常见的混联系统的系统可靠度和平均寿命的计算方法；范金城[2]给定了Bayes参数统计模型，讨论了参数连续型与离散型的后验密度函数；师小琳[3]在逐次截尾样本下，研究电子元件混联系统可靠性指标的估计问题；王玉芳[4]在定数截尾缺失的数据样本之下，研究了不可修n中取m串连续k失效系统的可靠性评估问题；而Sarhan A.M[5]利用贝叶斯和经验贝叶斯过程，进行了非参数的概率密度估计；孙天宇和Wu Shuo-Jye[6-7]都讨论了Bull-XII 分布在具有随机移走逐步增加截尾模型下可靠性指标的Bayes 估计，前者利用Monte Carlo 方法对各种估计结果进行了模拟分析，而后者还构建了精确的置信区间和区域的参数;蒋仁言等[8-10]分别探讨了利用蒙特卡诺模拟(MCS)方法，通过统计分析得到随机数的统计特征,解决可靠性问题与复杂的性能函数。与以上不同，本文利用Monte Carlo 方法建立随即模型，并基于逐步增加的Type-Ⅱ截尾，讨论了混联系统的系统可靠性指标的经验Bayes 估计。最后给出随机模拟的例子。

1 混联系统的蒙特卡诺方法及建模

1.1 蒙特卡诺方法

系统的可靠性建模，可以利用蒙特卡诺方法来完成，它是用来解决数学和物理问题的非确定性(概率统计的或随机的)数值方法，特别是当一个系统的输入变量较多，且比较复杂的情况下，用来建立系统输出的随机模型特别方便，因此它被广泛用于解决工程实际问题。由文献[9]，此方法包括仿真和综合两部分(如图1所示)，仿真部分将依据物理过程进行建模和计算，首先建立一个所测参数的数学模型，在运用伪随机方法服从给定分布的伪随机数来模拟实际的测量序列，最后按照所建立的数学模型对产生的随机数进行仿真计算，得出仿真的结果；而综合部分是根据仿真结果进行大样本集合的统计分析来估计真实结果。

图1 蒙特卡诺方法的仿真与综合图

1.2 混联系统的模拟方法建模

决定系统的输入与输出之间的功能模型或者数学模型完成这一过程，需要有关被研究的系统知识，即工程背景的知识。例如在液晶电视接收机中，其系统的部分核心包括公共通道，与此连接的有亮度通道、色度通道以及伴音通道等，组成的混联系统部分框图，如图2所示。

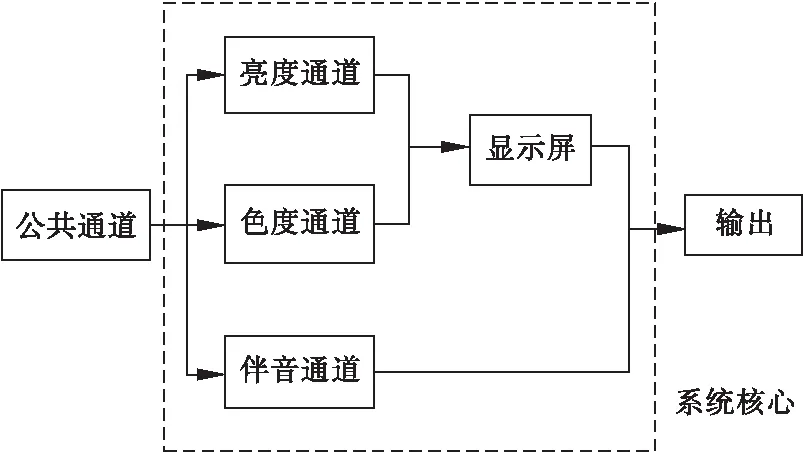
图2 液晶电视机组成部分框图

可以建立上述公共通道与输出之间的系统核心部分为混联系统模型，该模型抽象为系统包括四个元件构成(见图3)。

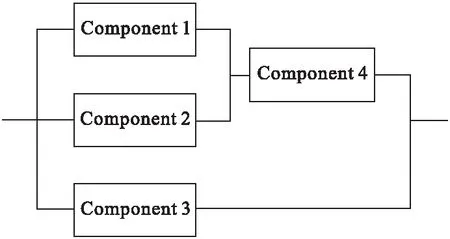
图3 混联系统图

元件所处的状况为系统的输入，系统所处的状况为系统的输出。设四个元件的可靠度分别为Ri=1-Fi(i=1,2,3,4)，其中Fi为元件的分布函数，则系统的输入与输出的关系为

R=1-{1-[1-(1-R1)(1-R2)]·R4}(1-R3)

(1)

用模拟的方法来求系统的可靠性。用xi(i=1,2,3,4)分别代表单元1，2，3，4的状态，并定义：xi=1(工作状态)和xi=0(失效状态)，生成四列各为n个均匀随机数，分别用pi(i=1,2,3,4)记这四列均匀随机数。这样有pi和xi的关系定义如下：

(2)

根据文献[8],用xs和xp分别代表由两元件x1和x2构成串联和并联系统的状态，

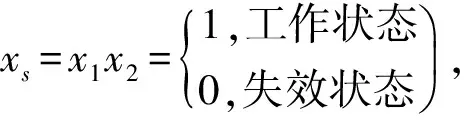
(3)

因此可以得到混联系统的状态:x=x4(1-x3)(x1+x2-x1x2)+x3

2 Type-Ⅱ截尾下的系统可靠性指标的Bayes估计

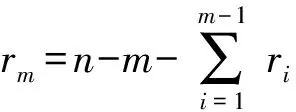
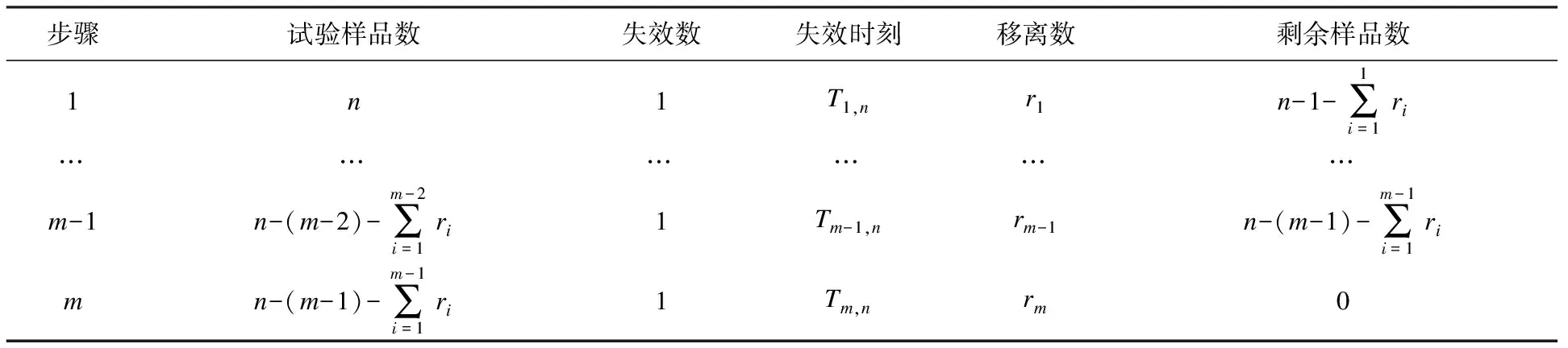
表1 逐步增加的Type-Ⅱ截尾寿命试验数据

令t=(T1,n,T2,n,…,Tm,n)。由文献[3]知在上述截尾样本下，样本t的似然函数为

(4)

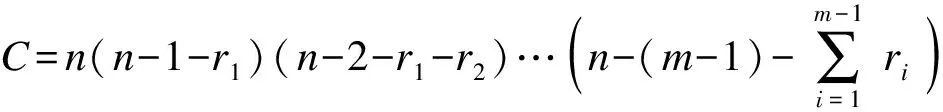
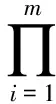
(5)

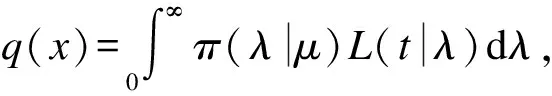
(6)

(7)

根据上述内容与图3所示的混联系统模型，可以假设各元件的寿命均服从参数为的指数分布，分布函数。F(t)=1-exp(-λt),(i=1,2,3,4)根据式(1)，可以得到系统的可靠度与平均寿命分别为

(8)

(9)

于是式(6)、(8)、(9)在平方损失下，混联系统可靠度和平均寿命的Bayes估计分别为

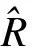
(10)

(11)

3 系统可靠性指标的经验Bayes(EB)估计

在上述混联系统中，得到了系统的可靠度和平均寿命的Bayes估计，此时超参数μ未知，单纯利用Bayes方法或极大似然方法效果都不理想，此时考虑将Bayes方法和极大似然方法结合起来，可以先用Bayes方法消去多余参数，然后利用极大似然方法估计其值。根据文献[11],由于只有很弱的先验信息，应该使用经验Bayes的思想从样本信息中构造先验分布，把μ看成是已定的参数，再结合样本及上述内容，λ的先验分布为π(λ|μ)，由于每个部件的寿命T服从参数为λ的指数分布，对λ积分可消去多余参数，因此可得T的边缘密度函数和可靠度函数分别为

=μ(t+μ)-2

(12)

=μ(t+μ)-1

(13)

在似然函数式(4)，取g(ti)=gT(ti),F(ti)=GT(ti),则似然函数为

(14)

下面用极大似然估计(MLE),求μ的极大似然估计。

(15)

(16)

根据文献[4]，由于g1(μ)>0，且g1(μ)→∞(μ→0),g1(μ)→0(μ→∞)

(17)

所以gi(μ)在(0,∞)内是严格单调递减的凹函数。同理可得g2(μ)>0，且g2(μ)在(0,∞)内同样也是严格单调递减的凹函数，有

(18)

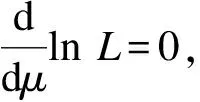
(19)

则将最终μ的迭代值μ*分别代入式(7)、(10)、(11)可得到混联系统元件的失效率、混联系统的可靠度以及平均寿命的EB估计，分别为

(20)

(21)

4 算例分析

如图3所示的混联模型中，设元件的可靠性为Ri，i=1,2,3,4,其中R1=0.75，R2=0.65,R3=0.83,R4=0.85,根据式(1)，可以得到此混联系统的可靠度为R=0.9619。

用蒙特卡诺方法来求系统的可靠性。根据式(3)中pi和xi的关系定义如下：

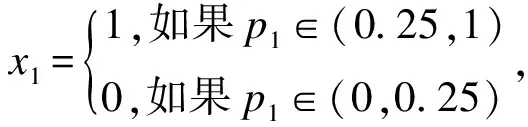
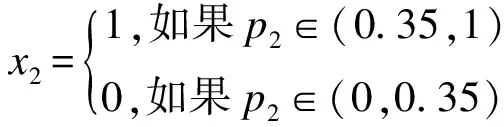
(22)

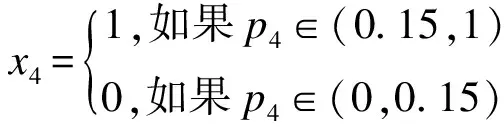
(23)

利用Excel里的RAND()函数可以产生(0,1)内的四列各为100个的均匀伪随机数，用上述记号pi,i=1,2,3,4分别记这四列均匀随机数。按照以上原理，在这100次模拟结果中，由出现x=0的次数为11次。所以模拟的混联系统可靠性为0.89，数据比较接近其理论真实值，若将模拟的次数增加时，如200次，500次，模拟结果将更为准确，如表2所示。

表2 蒙特卡诺模拟试验结果1

由表2可以看出，此混联系统随模拟次数的增加，通过计算，x=0出现次数也在增加，同样混联系统的可靠性逐渐提高，模拟计算结果更接近真实值。

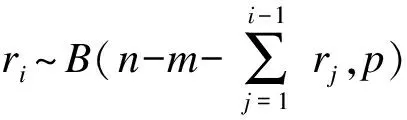
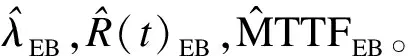
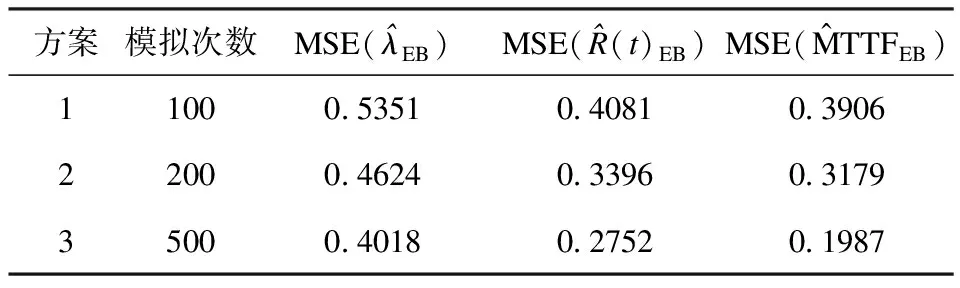
表3 蒙特卡诺模拟试验结果2

由表3所示的蒙特卡诺模拟结果看，混联系统的可靠度和平均寿命经验的Bayes与理论真实值的均方误差MSEμ较小，当模拟的次数增加时，此均方误差逐渐减小，即经验Bayes估计在理论基础上有明显的优越性。蒙特卡诺方法是一种仿真，通过建立模型产生相应分布的随机数，来模拟实际存在的过程，并且分析相关结果；而随机抽样统计分析是对实际数据的抽样分析；相比之下，前者能够比较逼真地描述具有随机性事物的特点及实验过程、受几何条件限制小、误差容易确定、程序结构简单易于实现等优点，说明该方法处理混联系统问题的正确性与可行性。在实际工程中，元件的失效率往往是未知的，特别是新研制的电子元件，根据上述元件失效率、系统可靠度和平均寿命的仿真结果，通过该解决可靠性问题的方法，有助于尤其对未知失效率的元件的情况进行分析，具有很大优势。

5 结束语

以复杂的混联系统为研究对象，利用Monte Carlo方法建立随机模型，并假定该模型具有随机移走的逐步增加Type-Ⅱ截尾。采用Bayes与极大似然估计相结合的方法，研究了可靠性的模拟问题，得到了混联系统部件的失效率、系统可靠度和平均寿命的经验Bayes估计，给出算例并分析。结果表明蒙特卡诺模拟方法能够较好地完成在给定条件下生成随机序列，进行系统的EB估计。研究混联系统的可靠性指标问题，可为可靠性工程问题提供一种解决方案，优化产品的质量。

[1] 曹晋华,程侃.可靠性数学引论[M].第二版.北京:科学出版社,2006:3-321.

[2] 范金城,吴可法.统计推断导引[M].北京:科学出版社,2001:215-246.

[3] 师小琳.逐次截尾样本下电子元件混联系统可靠性指标的EB估计[J].现代电子技术,2008,31(12):1-3.

[4] 王玉芳.定数截尾数据缺失场合下k(m)/n系统可靠性指标的经验Bayes估计[J].吉林师范大学学报(自然科学版),2012,11(4):26-31.

[5] Sarhan A M.Empirical Bayes estimates in exponential reliability model[J].Applied Mathematics and Computation，2003,135(2):319-332.

[6] 孙天宇,师义民,王亮.Burr-XII分布在具有随机移走逐步增加截尾模型下的可靠性指标的Bayes估计[J].系统工程理论与实践,2012,7(32):1476-1484.

[7] Wu Shuo-Jye,Chen Yi-Ju,Chang Chun-Tao.Statistical inference based on progressively censored samples with random removals from the Burr type XII distribution [J].Journal of Statistical Computation and Simulation,2007,77(1):19-27.

[8] 蒋仁言,左明健.可靠性数学模型与应用[M].北京:机械工业出版社,1999:52-66.

[9] 崔伟群,杭晨哲.基于蒙特卡罗方法评定不确定度中相关随机变量模拟[J].现代测量与实验室管理,2010,18(4):24-27.

[10]Ehsan Jahani,Mohsen A.Shayanfar,Mohammad A.Barkhordari.A new adaptive importance sampling Monte Carlo method for structural reliability[J].KSCE Journal of Civil Engineering,2013,17(1):210-215.

[11]Indrani Basak,Prasanta Basak,Balakrishnan N.On Some Predictors of Times to Failure of Censored Items in Progressively Censored samples[J].Computational Statistics & Data Analysis,2006,50(5):1313-1337.