双面槽药型罩参数对MEFP成型影响的数值模拟
张 健,邢 栋,相升海,张艳梅,张 岩,郑 凯
(1.沈阳理工大学 装备工程学院,辽宁 沈阳 110159 ; 2.东北工业集团有限公司吉林江机公司,吉林 吉林 132021; 3.中国人民解放军65041部队,辽宁 沈阳 110100)
随着科技迅猛发展,轻型装甲以及低空飞行目标将逐渐成为影响局部战争格局的重要因素,在单个EFP基础上发展起来的一种新型聚能装药技术MEFP逐渐成为攻击轻型装甲和低空飞行目标极为有效的手段。MEFP具有作战效率良好、杀伤半径较大、摧毁目标能力较强等优点。二十世纪八十年代初,国内外学者开始对MEFP战斗部技术进行研究[1]。国内学者主要对MEFP的成型、毁伤效能等方面进行研究[2-3],王猛等人[4]对整体三罩式MEFP战斗部进行了数值模拟及静爆试验;尹建平[5]对组合式MEFP成型弹丸参数进行了分析。
本文对战斗部装药长径比为1整体式双面刻槽药型罩的MEFP成型过程进行数值模拟,研究药型罩刻槽深度及曲率半径对MEFP成型的影响,得到刻槽深度及药型罩曲率半径比与子EFP长径比的关系曲线。
1 结构几何模型
通过在整体式药型罩内外面预制沟槽将药型罩划分为三部分,应用LS-DYNA软件对其建立如图1a所示的计算模型,球缺形药型罩内外圆半径分别为R1、R2,曲率半径比k=R1/R2,中心处开孔,紫铜作为药型罩材料,装药选用B炸药,起爆方式为底面中心点起爆。
数值模拟采用Solid164实体单元进行离散化,参见图1b,数值求解过程采用Lagrange方法,炸药模拟计算过程中采用MAT-HIGH-EXPLOSIVE-BURN材料模型[6]和JWL状态方程[7],JWL方程准确的描述了在爆轰驱动过程中爆轰气体产物的压力、体积、能量特性。A、B、r1、r2和ω为JWL方程中5个特征常数,参数值见表1;炸药密度ρ1、爆速D和爆压PCJ是B炸药的特性参数,见表2。

表1 B炸药JWL状态方程参数[8]

表2 B炸药参数
采用MAT-JOHNSON-COOK材料模型和EOS-GRUNEISEN状态来描述药型罩在爆轰波作用下的动力响应行为。药性罩密度ρ2、剪切模量G、弹性模量E、压力硬化指数N和应变率系数C为材料主要参数,见表3所示。Gruneisen状态方程参数见表4。γ0是Gruneisen gamma系数,T是Us-Up曲线的截距,S1、S2和S3是Us-Up曲线斜率的系数,α为γ0一阶体积校正量。

表3 药型罩材料参数

表4 Gruneisen状态方程参数
2 数值模拟结果与分析
2.1 MEFP的成型过程
对几何模型进行数值模拟计算,得到MEFP的成型过程,如图2所示。
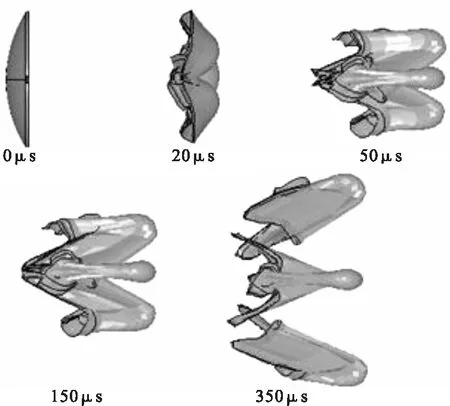
图2 MEFP成型过程仿真结果
图2中,0μs时刻为初始状态,药型罩在0~50μs之间受炸药爆炸产生的爆轰波冲击作用压垮变形,向前高速运动;同时药型罩受力拉伸变形,药型罩由刻槽处逐渐断裂分离;50~150μs之间,药型罩沿刻槽处继续分离,子EFP在爆轰压力作用下,头部凸起,尾裙打开;150μs时药型罩刻槽处已完全分离,形成了成型完整、飞行轴线之间形成一定的飞散角子EFP,成型完成;150~350μs之间,子EFP依靠惯性继续运动,按照各自轨道独立运行;同时根据子EFP从完全分离到数值计算结束过程中位移、形状的计算结果可以发现,子EFP外形及飞散角没有发生变化。为方便观察研究,本文取300μs时刻的数值模拟结果进行分析。
2.2 刻槽深度的影响
根据文献[4]中对药形罩的设计,k值设定为1.25,分析刻槽深度h对刻槽式MEFP成型的影响。分别选取h为1/8H、1/7H、1/6H、1/5H、1/4H、1/3H(H为药型罩厚度)进行数值分析。图3为产生爆轰作用后300μs时的6种数值模拟形态,图4为对应长径比曲线图。(在爆炸成型弹丸中,将成型完整EFP最大长度与EFP尾裙旋转圆直径之比定义为EFP长径比)。
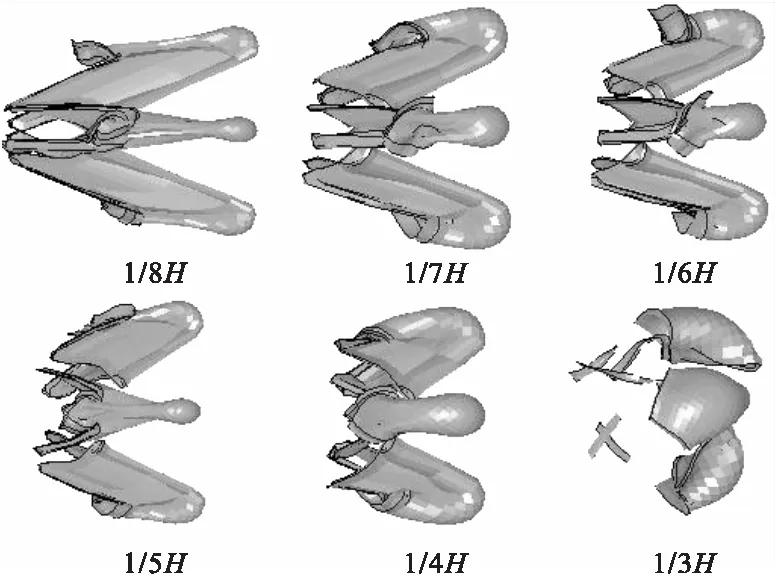
图3 不同刻槽深度MEFP成型完整后模拟图
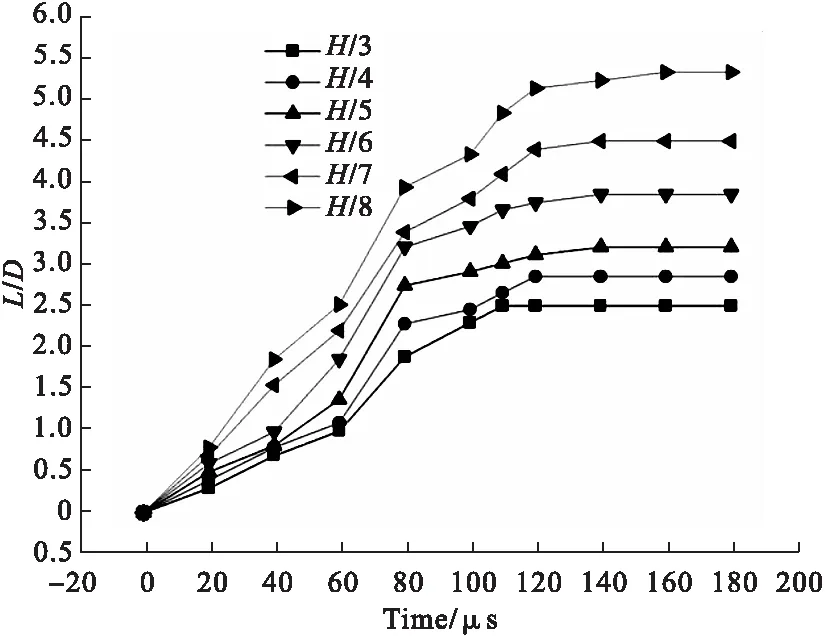
图4 不同刻槽深度子EFP长径比变化曲线
由图3、图4可知,当h值取1/8H时,子EFP的长径比达到5.7左右;随着h值的减小,长径比越来越大,长径比在h取在1/8~1/7H之间时,变化幅度最为明显,比值集中5左右,在这区间内h值随长径比变化的敏感度较高;当h取1/7~1/5H时,长径比变化幅度降低,说明在h取值较小时,h值的变化对长径比变化的敏感度较小;h取1/5~1/3H时,形成的子EFP长径比较小,形成外形整体趋于球状。
长径比值变化随h的增大而逐渐减小,从数值模拟过程可知,当h值较小时,爆轰压力作用在沟槽处使得药型罩在分离时得到较好的拉伸,使其头部半径逐渐变小,尾裙展开幅度越来越大,致其长径比越来越大;h值较大时,爆轰压力使得药型罩沿沟槽处迅速分离,子EFP的拉伸过程较短,且拉伸不充分,导致长径比很小。
2.3 药型罩曲率半径比的影响
在刻槽深度均为1/6H的情况下,变化k值的大小分析曲率半径比对MEFP成型的影响,300μs时仿真结果如图5所示,图6为对应长径比曲线图。

图5 不同曲率半径比MEFP成型完整后模拟图
由图5、6可知,k值取1.1~1.25时,子EFP长径比在2.0~3.0之间。其成型后没有尾裙,头部质量过于集中,易发生翻转。k取1.25~1.375时,长径比增大,成型发生了较为明显的变化,尾裙向后打开,头部被拉伸。当k值继续增大,取1.375~1.5时,长径比略有增大,但幅度不大。当k值由1.5增加到1.75时,长径比明显增大,在1.75时,子EFP被拉的过长,长径比达到5.6左右,易发生断裂现象。在不同曲率半径比下,长径比在成型完成之前始终呈增长趋势,爆轰波作用后50~100μs时,变化尤为明显,在同一时刻,药型罩曲率半径比略大,形成的子EFP长径比也略大。

图6 不同曲率半径比子EFP长径比变化曲线
2.4 综合分析
根据文献[5]中对EFP长径比的研究结论,可知弹丸长径比在3~5之间时,其外形特点有助于攻击反装甲目标。
结合本文2.2、2.3节中h与k值的变化情况,在研究单一方面因素h或k对子EFP长径比影响规律的基础上,对刻槽深度、曲率半径比与子EFP长径比的变化关系进行全面计算,利用Matlab软件建立起长径比与刻槽深度和曲率半径比的关系曲面拟合图像,如图7所示。

图7 长径比与刻槽深度和曲率半径比关系曲面
由图7可知,MEFP成型的子EFP的长径比随刻槽深度的增大而逐渐减小,随曲率半径比的增大而增大。当刻槽深度在1/7H~1/5H,曲率半径比在1.25~1.5之间时,长径比在3~5之间。
k值与h值的变化对MEFP的成型均有较明显的影响,两个因素发生变化时会引起爆轰波阵面作用于药型罩位置的改变、炸药爆轰能量损失大小的变化及子EFP飞散角的变化。
综上所述,曲率半径比为1.25~1.5、刻槽深度取在1/7H~1/5H时,双面槽药型罩MEFP形成的子EFP长径比在3~5之间,成型较为理想。
3 结论
(1)刻槽深度与曲率半径比的变化对MEFP的成型均有较明显的影响:刻槽深度增大,子EFP长径比减小;曲率半径比增大,形成子EFP长径比增大。
(2)刻槽深度为1/7H~1/5H、曲率半径比为1.25~1.5时,双面刻槽药型罩MEFP形成的子EFP长径比在3~5之间,成型较为理想。
[1] Ornelle Donneaud,Alain Tronche.EFP Shape Optimization in Accordance with Formation,Aero Dynamics and Terminal Ballistic Aspects[C].17th International Symposium on Ballistic.Midrand South Africa,1998:3-27.
[2] 尹建平,张洪成,付璐.多爆炸形弹丸性能参数灰关联分析[J].火力与指挥控制,2012,13(1):183-187.
[3] 赵长啸.起爆方式对整体式MEFP战斗部参数的影响[J].解放军理工大学学报,2012,13(5):559-564.
[4] 王猛,黄德武,罗荣梅.整体多枚爆炸成型弹丸战斗部试验研究及数值模拟 [J].兵工学报,2010,31(4):453-457.
[5] 尹建平.多爆炸成型弹丸战斗部技术[M],北京:国防工业出版社,2012.
[6] 迈耶斯 M A.材料的动力学行为[M].张庆明等译.北京:国防工业出版社,2006.
[7] 恽寿荣,赵衡阳.爆炸力学[M].北京:国防工业出版社,2005.
[8] 郭静,刘世兴,刘学深.双色激光场中1维共线氢分子离子的经典动力学研究[J].强激光与离子束,2006,18(7):1186-1192.

