状态跟踪问题的切换自适应控制策略
伍彩云,关 帅
(1.沈阳理工大学 装备工程学院,辽宁 沈阳 100159; 2.海军驻沈阳弹药专业代表室,辽宁 沈阳 110045)
在具有未知干扰输入的模型参考自适应控制系统中,往往首先给定与理想控制器结构相同参数可调的自适应控制器,通过设计自适应控制律在线调节自适应控制器的参数,使其逼近理想控制器效果,最终实现系统状态能够跟踪参考模型状态,使得状态跟踪误差收敛[1]。与传统控制的主要区别在于其存在自适应机制,在被控系统参数漂移和未知的情况下,可以提高系统的稳态精度和暂态性能[2]。目前一般采用李雅普诺夫理论、超稳定性理论和耗散理论等方法设计自适应控制律,主要目的是确保闭环系统信号有界的同时,也可以使状态跟踪误差收敛到零[3]。
一般情况下,一旦系统发生变化,其相应的自适应控制律需要重新设计。但是,在实际工程应用中,由于硬件实现及环境因素等方面的制约,系统相应的自适应控制律一旦设计使用之后,就不再便于重新设计和修改[4]。另外,有时通过理论所设计的单一自适应控制律的形式太过复杂,不便于硬件实现。此时,需要考虑利用已有的多个自适应控制律,使用多控制器的方法,实现状态跟踪。
多控制器方法之所以重要主要在于以下几个方面:首先,在传统的控制系统中,由于理论上所设计的单一的传统(连续或离散)控制器往往比较复杂,传感器和执行器的硬件实现受到一定的限制,导致该单一控制器难以在实际中得以使用,此时通过设计多个控制器切换实现单一控制器的功能[5];其次,当单一传统控制器或多个控制器分别无法镇定系统时,此时设计多个控制器及切换律或在有限个给定的控制器之间切换,使闭环系统稳定[6-7]。目前,多控制器切换作为一种混杂控制方式已经被应用到车辆控制[8]、机器人控制[9]、液压控制[10]以及交通控制[11]等方面。
对自适应控制系统,切换控制可以解决参数估计自适应控制中的稳定性和参数快变的问题。目前,切换自适应控制的研究以多模自适应控制为主,即为了改良自适应控制的暂态性能,通过对一个系统设计多个自适应控制器,根据每个控制器参数收敛程度来作为切换规则,其闭环系统实质为切换系统[12]。在模型参考自适应控制方面,对切换的系统,每个子系统设计自适应控制器,对非切换的系统,设计多个自适应控制器及切换律,都可实现闭环系统的状态或者输出跟踪。但是,给定系统及有限个自适应控制律,设计自适应控制器切换律,实现状态跟踪。针对此类问题,尚未见相关文献报道。
本文研究模型参考自适应控制系统的状态跟踪问题。当系统具有未知干扰输入时,考虑只允许使用有限个已知的自适应控制律,其任何一个都无法解决系统的状态跟踪问题,此时,采用自适应控制律凸组合的方法,利用李雅普诺夫稳定性理论,给出了一些充分条件,设计切换律,解决闭环系统的状态跟踪问题。
本文结果的主要特点在于,使用给定的有限个自适应控制律,设计切换律,解决状态跟踪问题。此外,该方法能够有效解决对于不同的系统,其相应的自适应控制律需要重新设计的问题,使模型参考自适应控制理论得到更广泛的应用。
1 问题描述
考虑系统是结构已知的线性系统,其状态方程为

(1)
式中:假设系统状态x(t)∈Rn可测;u(t)∈R为系统的控制输入;A∈Rn×n和B∈Rn是具有未知常参数的矩阵;d(t)∈R为系统的扰动输入。
(2)
式中:d0和dj是未知常参数;gj(t)是已知有界连续函数,j=1,2,…,M,且M>0。控制的目的是使系统(1)的状态能够跟踪某个参考模型的状态。
参考模型的状态方程为
(3)
式中:xm(t)∈Rn是参考模型的状态;Am∈Rn×n是Hurwitz矩阵;Bm∈Rn;r(t)∈R为输入信号。
为实现系统(1)的状态x(t)能够跟踪参考模型(3)的状态xm(t),定义系统的状态误差向量
e=x-xm
(4)
为达到状态跟踪的目的,引入可调的前馈增益矩阵K(t)∈R、反馈补偿矩阵F(t)∈R1×n和扰动补偿矩阵h(t)∈R,即:
u=K(t)r+F(t)x+h(t)
(5)
(6)
将式(2)、(5)和(6)代入式(1),可得闭环系统

(7)
由式(4)可得系统状态误差的动态方程

(8)
当满足匹配条件
Am=A+BF*
Bm=BK*

(9)

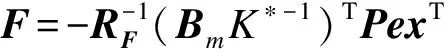

(10)
式中RF、BK、Rh0、Rhj和P为正定对称矩阵。
此时,闭环系统的状态误差动态方程为
(11)

本文考虑以下问题。给定有限组自适应律,其中任何一组都无法满足匹配条件(9),在不允许重新设计自适应律的条件下,如何设计自适应律的切换律,实现闭环系统的状态跟踪。即,给定多组自适应律


(12)

2 主要结果
本节将运用凸组合方法,对自适应律设计切换律。
定理1
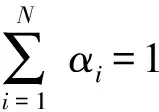


(13)
则可以设计切换律,使得系统(1)在给定控制器(5)、(6)和(12)的作用下,其闭环系统(1)的状态x(t)能够渐近跟踪参考模型(3)的状态xm(t)。
证明:利用凸组合构造误差增广系统
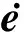
(14)


(15)
式(15)是关于自适应律(12)的凸组合。
构造李雅普诺夫函数
(16)
显然V>0。对式(16)沿着误差增广系统(14)和(15)取时间导数,有


(17)
由于
故式(17)又可以写成
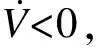
(18)
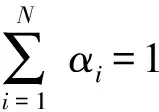
(19)
现在,对误差系统(11)和(12),考虑李雅普诺夫函数
(20)
当第s个自适应律被激活时,对式(20)沿着误差系统(11)和(12)取时间导数为
(21)
(22)
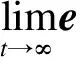
注1:对给定的自适应律(12),如果存在一个l∈N,使得第l个自适应律满足式(9),那么第l个自适应律可以解决状态跟踪问题。此时,可以选择αl=1,αk=0,l≠k此时定理1退化为中形式。
注2:当N=1时,该问题退化为传统单个控制器的设计问题。
3 仿真算例
考虑如下系统

其中系统的扰动输入为
d=0.001+0.01sin(0.001πt)+0.001sin(0.002πt)
参考模型为
本文研究当每个自适应律无法实现状态跟踪的情况下,通过设计切换信号实现切换系统的状态跟踪。因此,仿真中,在满足自适应律1和自适应律2对系统(1)、参考模型(2)和控制器(5)分别无法实现状态跟踪的条件下,选择自适应控制律调节矩阵分别为


其中,自适应律Ⅰ(i=1)为
Γ1=[49.4 49.4],Φ1=[4 4]
Ω1=[10 10],Ψ11=[40 40],Ψ12=[20 20]
自适应律Ⅱ(i=1)为
Γ2=[0.15 0.15],Φ2=[1.5 1.5],Ω2=[3.75 3.75],Ψ21=[15 15],Ψ22=[7.5 7.5]
下面分别对两个子系统进行仿真,具体仿真的软硬件环境为:intel(R)Core(TM)i5-2400 CPU、4GB内存、Windows 7操作系统、Matlab 7仿真软件,仿真时间选取0~60s.仿真的系统框图如图1所示。本文通过编写程序进行仿真,仿真界面如图2所示。具体结果如图3~7所示。图中r(t)为参考模型输入信号,u(t)为系统的控制输入,d(t)为系统的扰动输入,e(t)为状态跟踪误差。

图1 系统框图

图2 仿真操作界面
图3和图4为两个自适应律分别作用在闭环系统后的状态跟踪误差仿真曲线。从图3和图4可以看出,在任何单个自适应控制律单独作用于闭环系统时,闭环系统的状态跟踪误差没有收敛,即,闭环系统的状态无法跟踪参考模型状态。
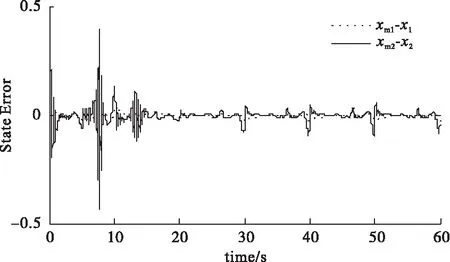
图3 状态跟踪误差(自适应律1(i=2))
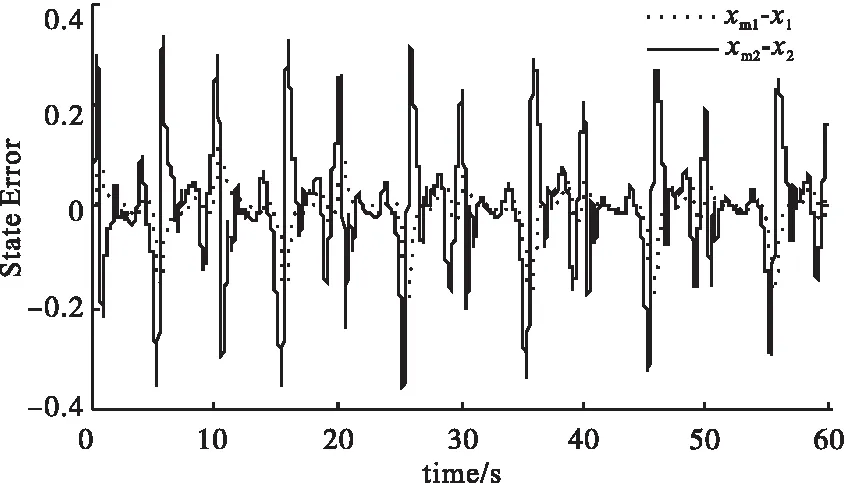
图4 状态跟踪误差(自适应律2(i=2))
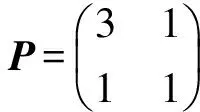

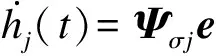
根据式(22),得到切换信号如图5所示。
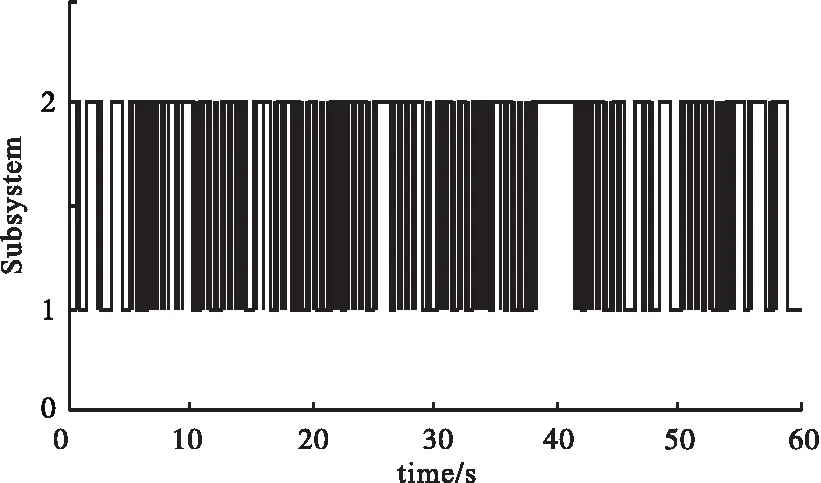
图5 切换信号
在该切换信号作用下,仿真得到切换控制曲线如图6所示。
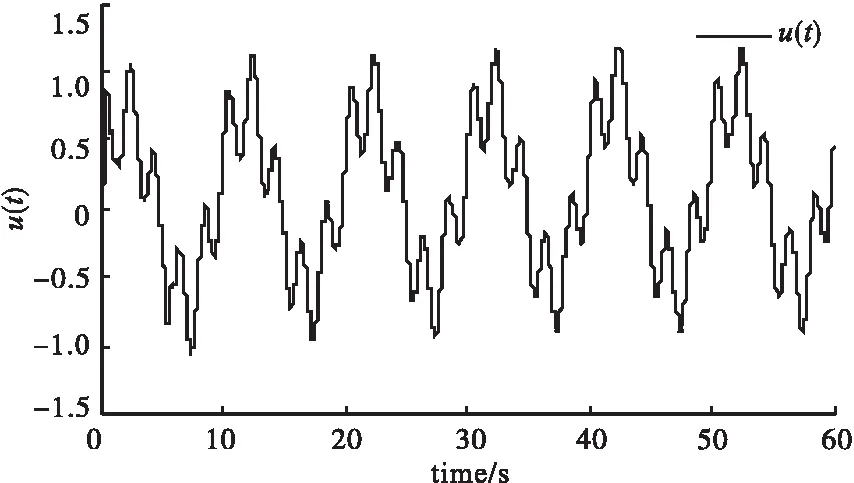
图6 控制曲线
从图6可以看出,自适应控制律是切换的,由此导致对系统施加的控制作用也是切换的,从而得到整个切换系统的状态跟踪误差曲线如图7所示。
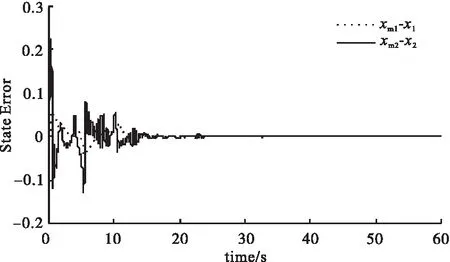
图7 切换系统状态跟踪误差(切换情况)
从图7中看出,该闭环系统的状态误差是收敛的,此时闭环系统的状态可以跟踪参考模型的状态,说明了该方法的有效性。
4 结论
本文研究了模型参考自适控制系统的状态跟踪问题。对给定的系统及有限多个自适应律,本文给出了一些充分条件,设计了切换律,通过自适应律切换,解决了闭环系统的状态跟踪问题。
[1] Tao G.Adaptive control design and analysis[M].A John Wiley & Sons.Inc.:New Jersey & Canada,2003.
[2] 侯砚泽,董朝阳,王青,等.不确定切换系统的鲁棒自适应控制方案[J].北京航空航天大学学报,2009,35(4):444-448.
[3] G.E.Valderrama,A.M.Stankovic,P.Mattavelli.Dissipativity-based adaptive and robust control of UPS in unbalanced operation[J].IEEE Transactions on Power Electronics,2003,18(4):1056-1062.
[4] Narendra K S,Balakrishnan J,Ciliz M K.Adaptation and learning using multiple models,switching,and tuning[J].Control Systems,1995,15(3):37-51.
[5] Liberzon D,Morse A S.Basic problems in stability and design of switched systems[J].Control Systems Magazine,1999,19(5):59-70.
[6] 祝庚,孙振东.切换线性系统的聚合优化[J].控制理论与应用,2013,30(7):815-820.
[7] 程代展,郭宇骞.切换系统进展[J].控制理论与应用,2005,22(6):954-960.
[8] Lygeros J,Godbole D N,Sastry S.Verified hybrid controllers for automated vehicles[J].IEEE Transactions on Automatic Control,1998,43(4):522-539.
[9] Jeon D,Tomizuka M.Learning hybrid force and position control of robot manipulators[J].IEEE Transactions on Robotics and Automation,1993,9(4):423-431.
[10]Stoten D,Bulut S.Application of the MCS algorithm to the control of an electrohydraulic system[C].in 20th International Conference on Industrial Electronics,Control and Instrumentation,1994:1742-1747.
[11]Tomlin C,Pappas G J,Sastry S.Conflict resolution for air traffic management:a study in multiagent hybrid systems[J].IEEE Transactions on Automatic Control,1998,43(4):509-521.
[12]翟军勇,费树岷.基于动态模型库的多模型切换控制[J].控制理论与应用,2009,26(12):1410-1414.

