同伦方法求解一类非凸规划问题的新的收敛性定理
孙文娟,赵巍巍
(1.沈阳理工大学 理学院,辽宁 沈阳 110159;2.吉林机械交通高级技工学校 教务科,吉林 吉林 132011)
同伦方法是20世纪70年代发展起来的一种求解非凸规划问题的大范围收敛方法。在数学规划、不动点计算、代数方程组求解等方面都有广泛应用。近年来,同伦方法的基本理论和应用也获得了极大的发展[1-5]。
同伦方法只能求得问题的K-K-T点,而人们更关心的是全局最优解或局部最优解。基于这一点,孙文娟等人[6-8]研究了在同伦映射为正则映射的条件下,同伦方法收敛到的K-K-T点的性质。文献[6]在同伦映射为正则映射的条件下,证明了同伦方法求解目标函数为凸的一类非凸规划时,得到的K-K-T点一定是局部极小解。而正则映射是一个较强的条件,很多算例显示,即使在不满足正则映射的条件下,同伦方法也能收敛到局部最优解,但目前理论上却没有相应的结论。本文研究对于目标函数为凸的一类非凸规划问题,如何在更弱的条件下判别出收敛点的类型,得到了同伦方法的一个新的收敛性定理,推广了文献[6]的结果。
1 预备知识
本文考虑下列非凸规划(NCP)问题
minf(x)
s.t.gi(x)≤0,i=1,2,…,m
(1)
式中:x∈Rn;f(x)为充分光滑凸函数;gi(x)(i=1,2,…,m)为充分光滑函数(不必凸)。
定义1 (K-K-T条件)若点(x,y)满足方程

(2)

定义2 设Ω为非空子集,x*∈Ω。非零向量d∈Rn称为在x*处的可行方向,若存在δ>0,使得x*+αd∈Ω,其中α∈(0,δ)。
为了方便,引入以下记号:
Ω={x∈Rn:gi(x)≤0,i∈{1,2,…,m}}为(NCP)的可行集;
Ω0={x∈Rn:gi(x)<0,i∈{1,2,…,m}}为(NCP)的严格可行集;
∂Ω=ΩΩ0为Ω的边界集;I(x)={i∈{1,2,…,m}:gi(x)=0}为在x点的紧指标集。
对K-K-T系统(2)构造组合内点同伦方程:
H(t,ω)=
(3)
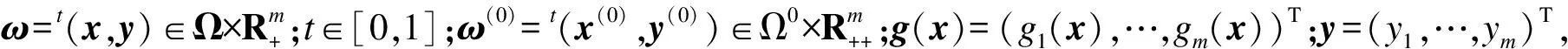
本文的基本假设如下:
假设1
(1)f(x)为充分光滑凸函数,gi(x)(i=1,2,…,m)为充分光滑函数;
(2)Ω0非空(Slater条件)有界;
(3){▽gi(x),i∈I(x)}为列满秩矩阵(约束正则性条件);
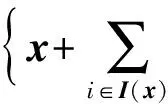
2 同伦方法的收敛性质

引理1 若H(t,ω)由式(3)定义,则
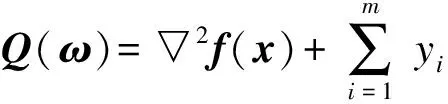
证明: 将式(3)中H(t,ω)分别对ω和t求导,易得引理1。
引理2 设x*是由同伦方法得到的K-K-T点,则对在x*点的每一个可行方向d,有
dT▽gi(x*)≤0,i∈I(x*)
证明对在x*点的每一个可行方向d,有
gi(x*+δd)-gi(x*)=δdT▽gi(x*)+o(δ2),i∈I(x*)
式中δ>0。若dT▽gi(x*)>0,i∈I(x*)成立,当δ充分小时,则有
gi(x*+δd)-gi(x*)>0
因为gi(x*)=0,i∈I(x*),故gi(x*+δd)>0,与d是x*点处的可行方向矛盾。
因此引理2成立。
定理2 若构造同伦方程为(3),且假设1成立,则由组合同伦内点方法得到的K-K-T点x*是问题(1)的局部极小点。
证明1)若x*∈Ω0,由于f(x)为凸函数,显然x*为局部极小点。
2)若x*∈∂Ω,则I(x*)≠∅。
当▽f(x*)=0时,显然x*为局部极小点;当▽f(x*)≠0时,对每一个可行方向d,由引理2及K-K-T方程,有
▽f(x*)Td=-y*T▽g(x*)Td≥0
故x*也一定是局部极小点。
综上所述,由组合同伦内点方法得到的K-K-T点x*是问题(1)的局部极小点。
3 结论
研究了对于目标函数为凸的一类非凸规划问题,同伦方法的收敛性质,得到了一个新的收敛性定理。证明了无论同伦映射是否为正则映射,同伦方法求解得到的K-K-T点都是问题的局部极小点,推广了文献[6]的结果。而对于一般的非凸规划问题,能否在比正则映射更弱的条件下,研究收敛点的性质,判别出收敛点的类型,将是今后的研究方向。
[1] FENG Guochen,LIN Zhenghua,YU Bo.Existence of interior pathway to aKarush-Kuhn-Tucker point of a nonconvex programming problem[J].Nonlinear Analysis,Theory,Methods and Applications,1998,32(6):761-768.
[2] YU Bo,WANG Yi.A new interior path following method for nonconvex nonlinear programming[J].Northeast.Math.J.,1997,13(3):257-260.
[3] LIN Zhenghua,LI Yong.Homotopy method for solving variational ineaualities[J].Journal of Optimization Theory and Applications,1999,100(1):207-218.
[4] XU Qing,YU Bo.Homotopy method for non-convex programming in unbounded set[J].Northeast.Math.J.,2005,21(1):25-31.
[5] 于波,商玉凤.解非凸规划问题动边界组合同伦方法[J].数学研究与评论,2006,26(4):831-834.
[6] 孙文娟,刘庆怀,王彩玲.同伦方法求解一类非凸规划问题的局部极小[J].吉林大学学报(理学版),2008,46(3):469-471.
[7] 孙文娟,李忠范,王彩玲,等.同伦方法求解无约束非凸优化问题的局部极小[J].东北师大学报(自然科学版),2009,41(3):17-20.
[8] 孙文娟,王彩玲.同伦方法求解无界域上非凸规划问题的收敛性定理[J].应用数学,2012,25(4):732-737.

