动态测验对“数学学习困难”儿童的进一步甄别*

2014-02-02 07:04:02张丽锦张臻峰

心理学报 2014年8期

张丽锦张臻峰

(1陕西师范大学心理学院, 西安 710062) (2上海图书馆, 上海 200031)

1 引言

学习困难(learning difficulties, 简称 LD)主要是指在与理解、使用语言(口头或书面)有关的一种或多种基本心理加工过程的失常, 这种失常可能表现为听说读写或数学计算上的能力缺陷(1997). Public Law 105–117.。数学学习困难(简称数学困难) (mathematics learning difficulties, MLD or MD)是学习困难的一种, 被认为与数学能力(计算加工技巧、数字事实提取、位值概念、数感)或/和一般加工能力(工作记忆、加工速度)缺陷有关(Chan & Ho, 2010)。数学困难儿童在解决简单数学问题时要付出比同龄人更多的努力,但效果和成绩却远不及他人。同时教师也容易给数学困难儿童贴上“落后”、“愚笨”等负性标签, 这种挫败感会使他们变得孤独离群并产生情绪烦恼和沮丧。这些都可能会进一步演变成行为问题, 进而影响其人生发展。因此有必要对这类儿童给予足够的关注。

数学学习困难与工作记忆密切相关(Rasmussen& Bisanz, 2010; Mabbott & Bisanz, 2008; Kimberly,Marcia, & Steven, 2010; Chong & Siegel, 2008),Siegel和Ryan (1989)最先探讨了数学学习困难儿童工作记忆的特点, 发现这些儿童在与数字有关的工作记忆能力方面明显不如正常儿童。中央执行系统是工作记忆模型中的核心, 负责各子系统之间以及它们与长时记忆的联系, 也负责注意资源的协调和策略的选择与计划(Jonides, Lacey, & Nee, 2005;Andrea, Elisa, Anna, Susnna, Franco, & Elisabetta,2006)。因此, 近些年有不少围绕数学学习困难儿童中央执行系统的研究。Bull等人以威斯康星卡片分类测验(WCST)考查了数学困难儿童的策略转换机制, 发现当数学困难儿童从一种分类范式转向另一种分类范式时, 表现出明显的困难。研究者认为这是由于这类儿童存在执行功能缺陷, 特别是策略转换和对优势反应的抑制能力不足所致(Bull,Johnston, & Roy, 1999)。同样, Passolunghi和 Siegel的研究也支持了Bull等人的观点, 证实数学困难儿童的抑制控制存在明显缺陷, 他们在需要抑制无关信息的工作记忆任务上易犯错、得分低, 并且这些儿童只在包含数字信息的工作记忆任务中表现落后, 在文字材料的工作记忆任务中则反应正常(Passolunghi & Siegel, 2001)。

除中央执行系统外, 数学困难儿童工作记忆的附属系统—— 视觉‒空间模板也存在不同程度的损害(Joni & John, 2008; Tracy, Susan, Hannah, &Julian, 2009; Passolunghi & Mammarella, 2011)。Cornoldi及其同事考查了11名数学困难儿童的视觉‒空间工作记忆, 结果发现这些儿童在所有4项视‒空工作记忆任务(图片任务、消极矩阵任务、积极矩阵任务和电视任务)上均存在显著缺陷(Cornoldi,Rigoni, Tressoldi, & Vio, 1999)。McLean和Hitch(1999)以 10个工作记忆任务分别考查数学困难儿童的视‒空、言语工作记忆和中央执行系统时也得到了类似的结果, 数学困难儿童不但中央执行系统存在明显缺陷, 而且在视‒空工作记忆上也是如此。一项对 26名数学困难儿童加工速度和工作记忆的研究(王恩国, 刘昌, 赵国祥, 2008)进一步发现, 这些儿童工作记忆的缺陷不仅表现在视‒空工作记忆和中央执行功能上, 还包括数字工作记忆能力的不足。上述研究结果均证实了数学学习困难与工作记忆下降之间的密切联系, 工作记忆是解释数学学习困难的重要原因之一。

差异模型(discrepancy models)是目前数学学习困难诊断中使用最多的标准。该模型认为数学成绩与一般智力水平之间的差异可以用来衡量儿童是否存在数学学习困难。尽管评估数学困难的模型一直在不断进步和发展, 先后有年级–水平离差法、期望公式法、标准分数法、回归分析法被陆续提出以提高差异模型的鉴别效果, 但相比较于标准分数法模型的计算复杂, 回归分析法模型的操作难度大,以及期望公式法的种类繁多不统一、研究者难以进行抉择, 年级–水平离差法因其概念直观、数学成绩易于收集而被研究者广泛采用(见 Bradley,Danielson, & Hallahan, 2002)。由于小学四年级是语文和数学成绩开始产生高低差别的关键时期(McLean & Hitch, 1999), 所以, 以往很多依据学习成绩和一般智力水平筛查数学困难儿童的研究所选取的最低年级都是小学四年级(如 Haworth et al.,2009; 刘昌, 2005; Proctor & Prevatt, 2003; Swanson& Howard, 2005)。本研究为了评估在传统筛查标准上加入动态测验指标的贡献, 也以四年级儿童为被试。

来看国内的情况, 自 1990年以来有关数学困难儿童的22个实证研究中, 3个采用了教师评定的单一标准, 3个使用了标准分数法, 16个用的是年级–水平离差法(见毕远, 张丽锦, 2014)。实际上, 由于数学困难的核心缺陷至今仍不明确(Mazzocco &Myers, 2003), 加之数学任务的多样性和复杂性,使得差异模型的甄别效果有时并不理想。最突出的问题就是：没有考虑不同年级和不同文化背景儿童接受教学干预的内容、水平和程度的不同。这样在实证研究的被试筛选中便几乎没有从学习能力和学习成绩发展变化的角度跨时段地筛选学习困难儿童。而集预测、诊断、矫治于一体的动态测验(见张丽锦, 盖笑松, 方富熹, 方格, 2003)则通过相继、多次、动态地测评认知改变来确定诊断结果。

动态测验(dynamic testing)是基于维果斯基的“最近发展区” (zone of proximal development, ZPD)理论而提出的指向于探查儿童潜在发展水平的测验方法。针对传统能力测验视能力为相对固定的、注重儿童现有认知水平的观点, 动态测验采用与智力测验相同或相似的项目作为评估工具, 摈弃传统测验中不指导、不干预的静态方法, 转而以过程评估的动态测评方式考查儿童的认知发展潜能, 旨在通过干预探查儿童认知发展的最高点, 以便更为公正、客观地评价儿童, 尤其是“弱势儿童”(disadvantaged children) (包括：低社会经济地位、新移民、学习困难、学习与智力落后、轻度精神障碍、自闭症和非主流文化的少数民族儿童等)的能力发展(张丽锦, 陈亮, 方富熹, 2011)。动态测验经历了 40多年的发展和完善, 对弱势群体的进一步甄别和潜能评估产生了巨大影响, 弥补了传统能力测验的不足, 使动态评估在特殊教育以及其他行为科学领域越来越多地受到心理测量学研究者、教育工作者的普遍关注(Ravi, 2001)。自动态测验兴起以来, 在对弱势群体进行细致甄别的研究中, 显示了非同一般的独特作用。比如, Ballesteros等人(Fernández-Ballesteros, Zamarrón, Tárraga, Moya, &Iñiguez, 2003)对健康老人、轻微认知损伤者(mild cognitive impairment, MCI)和早老性痴呆症患者(Alzheimer’s disease, AD)以动态测验范式检验学习潜能评估工具能否将这三类老人进行区分。结果发现, 健康老人的前测成绩显著高于MCI老人和AD老人, 而MCI老人和AD老人之间不存在差异; 但后测中动态测验的一系列指标显示, 除了健康老人的视觉‒空间记忆的前测成绩已达到“天花板效应”而使其“获得分”低于MCI老人外, 其他三个测验中均是健康老人的“获得分”最高, 其次是 MCI老人,最后是AD老人。尤其是词语记忆测验中的延迟后测成绩, 三组被试的差异最大。进一步的统计显示,93% AD老人的延迟回忆成绩比前测分数低, 而相应的人数比例在健康老人中仅有3%、MCI老人中有 42%。该研究证明了动态测验的延迟后测指标,而非传统静态测验的前测指标在预测早老性痴呆症者认知潜能的显著效用。Swanson和 Howard(2005)对 45名有阅读困难症状的学习困难儿童进行动态测验以便对之进一步甄别, 结果发现动态测验指标能更好地预测和解释阅读困难儿童、数学和阅读困难儿童的分数变异, 对明确区分不同程度的学习困难儿童有更大的贡献。回顾动态测验的发展,它的应用涉及到了多种弱势群体, 包括脑损伤病人(Haywood & Tzuriel, 2002)、精神分裂症患者(Sclan,Johnson, & Haywood, 1986)、低社会经济地位儿童(Tzuriel & Klein, 1985; Tzuriel, 1989)、非主流文化背景儿童(Tzuriel & Kaufman, 1999)、智力落后儿童(Ferretti, Butterfield, Cahn, & Kerkman, 1992)和学习困难儿童(Swanson & Howard, 2005), 甚至还包括期望改变认知能力的企业员工, 乃至超常儿童(Feuerstein, Miller, Rand, & Jensen, 1981)。Swanson认为传统的评估方法不能评鉴儿童信息加工的潜能, 也不能将真正的学习困难儿童与低成就(low achievement)儿童区分开来(Swanson, 1996)。由于学习困难主要是因信息加工过程存在缺陷而使潜能发挥受到限制, 那么, 动态测验便有望通过干预训练考查和评估这类儿童的认知潜能, “Swanson认知加工测验” (S-CPT) (Swanson, 1996)采用的动态评估范式对个体工作记忆的认知加工过程进行评估,可以有效区分不同程度的学习困难儿童。

因此, 本研究试图采用S-CPT动态测验范式来进一步区分数学学习困难儿童。首先, 通过探明动态评估与数学成绩之间的因果关系来验证动态测验对儿童数学成绩的预测作用; 其次, 通过比较经动态测验所区分的不同程度数学困难儿童与正常儿童之间的 S-CPT分数和他们一年后的数学期末考试成绩来进一步验证动态测验范式对甄别数学学习困难儿童的效用。

2 研究方法

2.1 被试

选取城市2所普通小学四年级数学学习困难儿童 30人(女生 13人), 平均年龄和标准差是10.00±0.73岁。同时选取智力匹配的同年级正常儿童30人作为对照组(女生 13人), 平均年龄和标准差是10.38±0.99岁。

2.2 实验材料

(1)瑞文标准推理测验(张厚粲, 王晓平, 1986)：包含5个单元的60张图片。本研究在预试阶段从瑞文标准推理测验中挑选了与四年级儿童认知能力相匹配的 32个项目, 从这些项目中再进行筛选,筛选的原则是：①通过率处于20%～80%; ②被试推理成绩呈正态分布, 最终从 5个单元中确定了 20个项目(A系列项目为A、A、A、A; B系列为B、B、B、B; C 系列为 C、CCC; D 系列为D、D、D、D; E 系列为 E、E、E、E), 构成认知水平的图形推理测验。答对1题计1分, 满分20分。将原始分转换成平均分为100、标准差为15的标准分再进行后续的被试筛选。

(2)Swanson认知加工测验(Swanson Cognitive Processing Testing, S-CPT) (Swanson, 1996)：该测验为标准化动态测验工具, 旨在考查被试的工作记忆潜能, 其基本假设是认知技能的学习与个体工作记忆有关。本研究使用S-CPT中的4个子测验—— ①押韵词测验(rhyming words)：含9个项目, 考查关于韵脚相似词汇的听觉复述能力; ②听觉数字顺序测验(auditory digit sequence)：11个项目, 考查对包含数字的短句的回忆能力; ③视觉矩阵测验(visual matrix)：9个项目, 考查对视觉矩阵顺序的回忆能力; ④识图和方向测验(mapping and directions)：9个项目, 考查被试对视觉‒空间顺序和方向的记忆能力。各个子测验的项目难度逐级增加。

2.3 实验程序

2.3.1 被试筛选

参照前人使用的年级–水平离差法的筛选标准(Proctor & Prevatt, 2003; Swanson & Howard, 2005;刘昌, 2005; 朱莉琪, 1999)选取数学学习困难儿童。第一步, 在银川市选取两所普通全日制小学, 在秋季开学初对四年级学生(330人)整班施测瑞文标准推理测验; 第二步, 收集这些学生三年级期末考试的数学和语文成绩, 将每个班数学成绩处于后25%、语文成绩处于中等或中等以上的儿童名单(42人)列出; 第三步, 将所列名单交给数学老师和/或班主任老师进行评定, 将数学成绩有较大波动的儿童排除, 将可能存在感官缺陷和情绪困扰的儿童排除, 同时排除智力落后儿童(瑞文标准推理测验低于90分); 第四步, 选取到了30名数学学习困难儿童,同时从上面的42人之外另选30名智力匹配的同年级儿童作为对照组, 平衡两组被试的性别比例。

2.3.2 S-CPT的施测

通过实验组对照组“前测–干预–即时后测–延迟后测”范式探查数学困难儿童在S-CPT中工作记忆的认知潜能。

(1)前测：在安静的房间对所有被试进行一对一的4个子测验的施测, 施测顺序为押韵词测验、听觉数字顺序测验、视觉矩阵测验、识图和方向测验。测验前主试宣读指导语(“一会儿我会给你读一些字、词、句子或看一些图片, 你尽量记住我给你读的和看的内容。有些问题对你来说可能很简单, 但也会有些问题相对你们这个年龄来说比较难, 所以回答不上来也没有关系, 你只要尽力回答就可以了。注意, 在你回答不上来的时候, 我会给你一些提示帮助你回忆。一些提示对你来说会很有帮助,另一些可能对你帮助不大, 我想了解一下哪些提示对你来说比较有用。好！现在可以开始了, 你准备好了吗？”), 如果被试没有听懂就再重复一遍。正式测验时, 每个题目施测步骤如下：①给被试呈现题目; ②要求被试回答有关该题目的加工问题(例如：对于听觉数字顺序子测验的第1题, 在呈现题目后询问被试“医院在什么街上？”); ③如果子测验(如, 视觉矩阵测验、识图和方向测验)需要被试选择策略, 则要求他们在10秒钟内从4个备选策略中选择 1个自己最倾向使用的策略(这些策略用图片的形式呈现, 包括：(ⅰ)重复记忆; (ⅱ)组块记忆; (ⅲ)相关内容联想; (ⅳ)相关事件联想); ④如果被试回答的加工问题是错误的就转到下一个子测验; 如果回答的加工问题是正确的, 则要求其回忆题目。记录每个被试在4个子测验的成绩, 即初始分。

(2)干预：干预的内容与被试的错误相匹配, 主试将被试犯错误(遗漏或错误回忆)的地方在主试记录册上作准确记录, 以便随后进行恰当的即时干预。干预时按顺序从划有斜线的题项最后面开始,然后再提示题项的最前部分, 继而提示题项的中间部分, 最后提示整个题目(共 4级提示) (如, 报酬/忧愁/复仇, 一级提示：告诉被试最后出现的是

复仇;

二级提示：告诉被试最先出现的是报酬; 三级提示：告诉被试中间出现的是忧愁; 四级提示：重复读一次题目)。每一级提示后被试要对所干预的项目再进行完整回答(即, 回忆或复述)。如果在同一个项目中给被试提供了所有的4个提示或在两个前后连续的题目上都提供了3个提示, 就要转向下一个子测验。根据被试在各子测验上接受提示的次数记录被试的指导分。(3)即时后测：主试根据被试的错误位置提供了一系列线索和帮助后, 记录被试在各子测验重测的最高分数, 即

获得分

。(4)延迟后测：被试在所有4个子测验施测结束后立即进行后测并记录

保持分

, 测题为儿童在干预帮助下仍出现错误的各子测验题目。

2.3.3 S-CPT的分数类型、计分及分数转化

体现S-CPT整套测验结果的基本分数有3种：

初始分

：即前测分数, 指在没有提示帮助的情况下被试的最高水平, 这也是传统静态测验所测的水平。计分标准为, 答对1题计1分, 4个子测验的分数范围分别是：押韵词测验、视觉矩阵测验、识图和方向测验均为 0～9分, 听觉数字顺序测验 0～11分;

获得分

：被试在直接干预或帮助条件下的最高得分, 反映了其加工潜能的至高点。计分标准同初始分;

保持分

：评估被试内化或同化外界干预或提示的能力, 延迟后测时如果被试能够正确回忆, 则保持分与获得分相同; 如果不能正确回忆, 则保持分与初始分相同。保持分的低分显示了对干预或提示的高依赖性, 说明需要较多的提示和帮助; 高分则反映了低依赖性, 说明需要较少的提示和帮助。S-CPT在基本分数之外还有延伸出来了4个动态测验分数：

加工差异分

：获得分与初始分之间的差异,反映了被试加工潜能的宽度或弹性指标;

加工稳定

分：保持分与初始分之间的差异, 反映被试在没有干预帮助的情况下保持其最高水平的表现能力是否处于平均水平之上;

策略效能分

：评估被试的有效加工策略或知识, 计分方式需根据《S-CPT手册》将被试在具体测验中所选择的策略的平均等级转化为策略效能分;

指导效率分

：反映在提示或帮助条件下被试获得最高分所需的提示数量, 计分方式为将被试在各子测验中所需提示帮助的次数相加,分数越高表明被试在解题过程中更依赖提示和帮助。当转化为标准分时其计分方式为反向计分,即分数越高表明被试更少依赖提示和帮助, 效率越高。

根据《S-CPT手册》中的9个参考表, 可将被试的原始分数转化为量表分, 再将量表分转化为平均数为100、标准差为15的标准分。押韵词、视觉矩阵与识图和方向三个子测验的原始分的分数的范围是0～9, 相对应的量表分的范围是0～20, 对应的标准分的范围是 34～165; 听觉数字顺序测验的原始分数范围是 0～11, 相对应的量表分和标准分的范围同样是0～20和34～165。

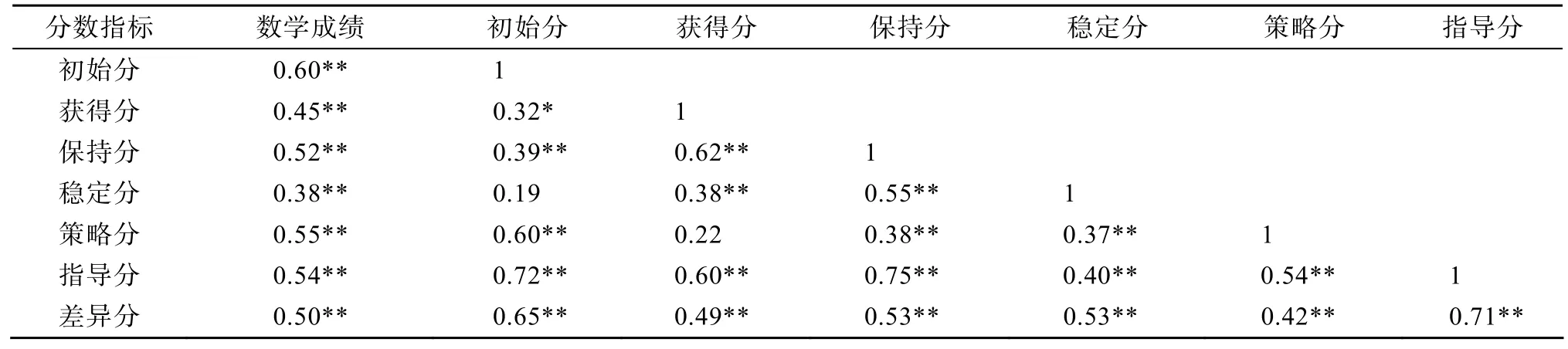
表1 数学成绩、动态测验各个指标之间的相关分析(N=60)

3 结果

3.1 动态测验对儿童数学成绩的解释意义和贡献

为探明动态测验的各个指标与儿童数学能力是否存在关系, 本研究基于儿童的数学成绩对其数学能力具有预测作用, 将被试四年级的8次数学考试成绩的平均分作为考查儿童数学能力的指标。首先, 对被试动态测验的各个分数与其数学成绩进行相关分析(见表 1), 发现动态测验的所有得分与数学成绩均有显著的正相关, 因此可以进一步考查动态测验各分数与数学成绩之间的回归关系。

然而, 从表1的结果看, 除了初始分与稳定分、获得分与策略分之间无相关外, 其他各分数之间均有较高的相关, 说明各分数之间可能存在较严重的多重共线性。对多重共线性进行检验发现, 除常数项特征根大于7外, 其余的动态测验指标特征根均小于0.5, 并且除常数项的条件指数等于1外, 其余的指标条件指数均大于 30, 表明各分数之间确实存在较严重的多重共线性。

为避免多重共线性对结果的影响, 借鉴Swanson和 Howard (2005)对动态测验各类分数进行因素分析的方法对变量进行整合, 以检验究竟是动态测验哪类分数对儿童数学成绩具有预测作用。首先,

KMO

=0.76, Bartlett球形检验χ=236.44 (

< 0.01),说明数据适合做因素分析。进行主成分分析, 选择正交旋转, 提取特征根大于1的因子共2个, 累积方差解释率为72.61%, 说明提取的2个因子能较好地解释变量的作用。由于动态测验的差异分和指导分出现了双载荷现象, 将其删除, 最后发现初始分和策略分聚敛在一个因子上, 反映了无干预或帮助条件下被试的工作记忆能力, 故将其命名为“原有认知能力”, 解释率为 32.84%; 获得分、保持分和稳定分聚敛在一个因子上, 反映了给予动态干预后被试所达到的潜在发展水平, 将其命名为“潜在认知能力”, 解释率为39.77% (见表2)。

表2 动态测验得分的因子结构及各变量的因子载荷(N=60)

将原有认知能力、潜在认知能力与儿童的数学成绩之间进行相关分析发现, 原有认知能力和潜在认知能力均与儿童数学成绩有显著的正相关,

=0.57,

=0.44,

s < 0.01, 表明原有认知能力、潜在认知能力越高, 儿童的数学成绩就越好。为进一步考查原有认知能力、潜在认知能力、原有认知能力加潜在认知能力对儿童数学成绩的预测作用, 以上述 3个变量为自变量, 以儿童的数学成绩为因变量进行阶层回归分析(见表 3)。结果发现单个变量和变量组合都对数学成绩有显著的预测作用, 且模型3的决定系数

=0.51, 该值远大于模型1和模型2的决定系数, 表明在数学学习困难分类方式的基础上加入动态测验的指标能更好地预测儿童的数学成绩。

3.2 动态测验进一步甄别和分类数学学习困难儿童的有效性检验

3.2.1 动态测验分数指标对数学学习困难儿童的进一步区分

为了进一步将数学学习困难儿童作不同程度/水平的区分, 以潜在认知能力指标(即, 获得分、保持分和稳定分)作为进一步鉴别的依据, 将正常儿童的潜在认知能力进行区间估计, 找出正常儿童潜在认知能力的下限。结果发现, 数学困难儿童组潜在认知能力成绩为：

=93.41,

=9.20, 其95%置信下限为90分, 置信上限为96.88分; 正常组儿童潜在认知能力为：

=102.10,

=4.92, 其95%置信下限为100.33分, 置信上限为104分。两类儿童在“潜在认知能力”得分上差异显著,

(1, 58) =20.96,

< 0.01,

=0.27; 数学困难儿童显著低于正常儿童。由此推测, 如果数学困难儿童的潜在认知成绩高于 100.33分则落在了正常儿童的认知潜能发展范围之内, 而低于100.33分则说明其潜能还没有达到正常儿童的潜能水平。据此, 可以从潜能角度将数学困难儿童区分为“发展落后”和“发展缺陷”两个水平。基于上述标准, 30名数学困难儿童被划分到“发展落后”组11人、“发展缺陷”组19人, 所占比例分别约为37%和63%。

表3 预测儿童数学学习成绩的模型检验(N=60)

3.2.2 在动态测验各类分数上三类儿童的成绩比较

对不同类别儿童在 S-CPT动态测验三类基本分数的表现分别进行单因素方差分析发现(见图 1),三类儿童在初始分上存在显著差异,

(2, 57) =17.98,

< 0.01,

=0.39。事后检验表明, 正常儿童的初始分显著高于“发展落后” (

< 0.05)和“发展缺陷”儿童(

< 0.01), “发展落后”儿童的得分显著高于“发展缺陷”儿童(

< 0.05)。三类儿童在动态测验的分数指标获得分和保持分上均差异显著(

(2,57)=14.78,

< 0.01,

=0.34;

(2, 57) =39.13,

< 0.01,

= 0.58), 具体来看, 正常儿童和“发展落后”儿童得分均显著高于“发展缺陷”儿童(

s < 0.01), 前两者之间没有显著差异。为进一步考查三类儿童内化干预的能力和潜能宽度的差别而逐个进行方差分析, 结果表明(见图2), 三类儿童在稳定分上存在显著差异,

(2, 57)= 14.03,

< 0.01,

=0.33; 事后检验发现, “发展落后”组与正常组之间没有差异, 且两者得分都显著高于“发展缺陷”组(

< 0.05)。三类儿童在差异分上同样差异显著,

(2, 57)=22.84,

< 0.01,

=0.45,且其表现趋势与稳定分相似。再看三类儿童对干预的敏感程度和策略使用情况, 在指导分上有显著差异,

(2, 57)=26.07,

< 0.01,

=0.48, “发展落后”组和正常组之间没有差异, 两者得分都显著高于“发展缺陷”组(

< 0.05), 表明“发展缺陷”儿童需要更多的提示和帮助; 策略分上也同样存在显著差异,

(2, 57)=13.73,

< 0.01,

=0.33, 正常儿童的策略分显著高于另两类儿童(

< 0.05), 而“发展落后”与“发展缺陷”儿童之间无显著差异, 表明正常儿童工作记忆的加工策略显著优于不同程度的数学学习困难儿童。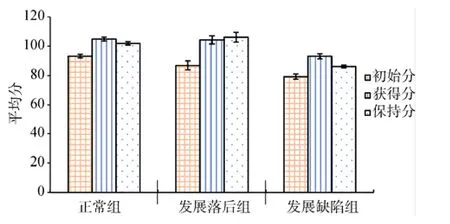

图1 三类儿童分别在初始分、获得分和保持分上的得分比较

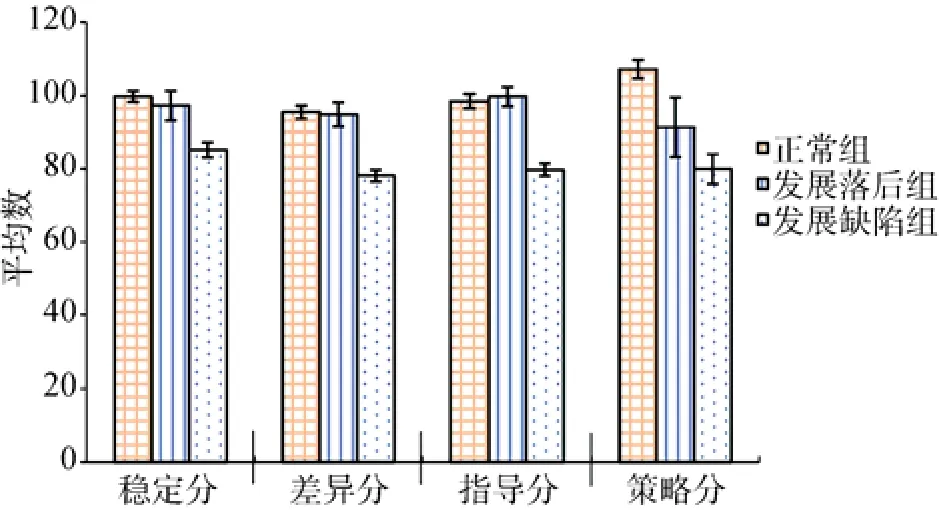
图2 三类儿童分别在稳定分、差异分、指导分、策略分上的得分比较

3.2.3 动态测验区分的三类儿童在三、四年级时数学成绩的变化

为考查动态测验分类标准下的三类儿童的数学成绩变化, 收集他们三、四年级学年末的数学成绩。为便于两次成绩比较和取消负数、小数, 将其转化为以100为平均数, 以15为标准差的标准分数,进行3(被试：“发展落后”组、“发展缺陷”组、对照组) × 2(年级：三、四)的重复测量方差分析。结果发现(见图3), 年级主效应显著,

(1, 57)=14.11,

< 0.01,

=0.20, 四年级时儿童数学成绩显著高于三年级时; 类别主效应显著,

(2, 57)=55.18,

<0.01,

=0.66, 对照组数学成绩显著高于“发展落后”和“发展缺陷”组(

< 0.05;

< 0.01), “发展落后”儿童的数学成绩显著高于“发展缺陷”儿童(

<0.05); 年级与类别交互作用显著,

(2, 57)=8.84,

< 0.01,

=0.24, 简单效应检验发现, 三年级时,对照组儿童数学成绩显著高于“发展落后”和“发展缺陷”儿童,

(2, 54)=49.68,

< 0.01, 后两类儿童之间没有差异; 到了四年级, 对照组儿童与“发展落后”儿童数学成绩之间没有差异, 且都显著高于“发展缺陷”儿童,

(2, 54)=45.90,

< 0.01, 说明“发展落后”数学困难儿童的数学成绩有了明显的增长性改变, 而“发展缺陷”儿童没有变化。

图3 三类儿童三、四年级数学成绩比较

4 讨论

4.1 动态测验分数对预测儿童的数学成绩的贡献

从上世纪 60年代对学习困难(包括数学困难)进行识别、诊断和训练开始到现在, 数学困难鉴别标准经历了从能力‒成绩差异模型到干预反应范式(response to intervention, RTI)的重要改进。动态测验和干预反应范式的鉴别手段并不是完全摒弃传统的诊断标准, 而是在传统诊断标准的基础上经过动态评估以便更为准确、细致地鉴别和区分学习困难儿童(Grigorenko, 2009)。在这个理论背景下, 本研究基于以往数学学习困难儿童存在工作记忆缺陷的主张(如 Bull et al., 1999; Cornoldi et al., 1999;Passolunghi & Siegel, 2001), 采用动态测验的评估方法, 探讨动态测验能否进一步快速、准确地区分基于能力‒成绩差异模型筛查出的数学困难儿童。

S-CPT是一个公开发表的动态测验工具, 包含了11个子测验, 涉及音韵、视觉矩阵、绘图、听觉数字顺序和故事复述等多个领域, 考查6.5到70岁人群视觉‒空间工作记忆和言语工作记忆的潜在能力。根据S-CPT各子测验所适合的年龄范围, 本研究选取了 4个适合四年级儿童的子测验—— 押韵词测验、听觉数字顺序测验、视觉矩阵测验、识图和方向测验。通过对比数学困难儿童与正常儿童在S-CPT上的各种分数指标(初始分、策略分、获得分、保持分、稳定分等), 并以因素分析的方法得到了影响儿童数学成绩的两个因素：原有认知能力和潜在认知能力, 分别反映的是无提示干预下儿童已有的工作记忆水平和在帮助、提示下儿童能够达到的潜能高度。

基于动态测验的评估“儿童潜能”的有效途径是考查他们在有、无干预条件下发生认知改变的主张(Swanson & Howard, 2005), 本研究又进一步分析了数学成绩对原有认知能力和潜在认知能力的回归, 得到了有意义的结果：仅考虑儿童原有认知能力对数学成绩的预测, 其解释力为 31.9%, 说明传统静态测验对儿童数学成绩的良好预测。但是,在考虑了潜在认知能力这一动态测验的变量后, 其解释力有了显著提高, 达到一半多(50.9%)。原有能力是儿童已有的认知能力, 即现有能力水平。关注儿童现有水平的能力/智力测验(即“传统测验”或“静态测验”)的构建就是基于智力可以预测儿童未来学校学习(表现为学业成绩)的胜任状况, 本研究中原有能力对数学成绩的31.9%的预测也证明了这一点。那么, 智力测验所涉及不到的对学业成绩有影响的能力因素还有什么, 也应该是研究者关注的内容。动态测验评估和标定潜能的各类指标(增长分、提示分、获得分、稳定分等)反映的是个体经干预后能力的增长和进步、掌握后的迁移和应用,可以看作是个体的潜在学习能力(见张丽锦等,2003), 它对儿童学习成绩的进步和提高是有意义的。正如本研究结果所示, 潜在认知能力对数学成绩的预测有19%。以往动态测验研究发现, 相比较于静态测验成绩, 动态测验成绩对儿童学习成绩具有更好的预测作用(Fabio, 2005; Serge, Kern, Mintz,& Green, 2005), 这与本研究的结果略有不同。分析原因, 以往研究涉及到的学业成绩是多学科学业成绩的综合, 而本研究考查的只是数学成绩。众所周知, 数学学科相对于其他学科对个体相匹配的先天能力水平更有要求, 以往探究数学认知能力内部机制的许多研究也支持了主张先天数量表征缺陷的“数字模块缺陷假说” (如 Butterworth, 2008;Landerl, Fussenegger, Moll, & Willburger, 2009;Landerl & Kölle, 2009)。因此, 这里原有能力的预测值高是可解释的。

总之, 本研究的结果可以证明加入动态测验后,原有能力加上潜在能力可以更大程度地预测儿童的数学成绩, 由此也进一步证明动态测验是传统静态测验的有益补充。

4.2 动态测验可以快速、准确地进一步区分数学学习困难儿童

正如Swanson (Swanson, 1996; Swanson &Howard, 2005)所说, 传统的评估方法不能考量儿童信息加工的潜能, 也不能将真正的学习困难儿童与低学业成绩儿童区分开来, 真正的学习困难主要是因信息加工过程存在缺陷而使潜能发挥受到限制。本研究通过动态测验鉴别出两类数学困难儿童后, 进一步对鉴别结果进行了验证。将数学困难的“发展落后”儿童和“发展缺陷”儿童与正常儿童的动态测验各个分数进行对比, 试图证明动态测验指标进一步鉴别和区分数学困难儿童的有效性。

首先, 初始分、获得分和保持分是动态测验范式中最基本的指标, 数学困难“发展缺陷”儿童的初始分明显低于“发展落后”和正常儿童, “发展落后”儿童与正常儿童也有明显差异, 初始分上的差异体现的是未经干预各组被试工作记忆的不同水平。再看获得分和保持分这两个反映干预后成绩增长和认知改变的动态测验指标, “发展落后”儿童较“发展缺陷”儿童有了显著提高, 甚至达到了正常儿童的水平(见图 1)。该结果证实了 Geary等人的一系列研究结果(Geary, 1990; Geary, Brown, &Samaranayake, 1991; Geary, Hoard, & Hamson, 1999;Geary, Hamson, & Hoard, 2002), 即传统基于数学成绩的甄别方法包含了数学“发展落后”儿童, 而这些儿童不是真正的数学困难, 可能是由于环境、情绪、文化等影响而导致的数学落后。比如, Geary(1990)将数学困难儿童分为提高组(一年级数学成绩低但二年级明显提高)和无提高组(一、二年级成绩都低), 干预后发现无提高组数学困难儿童在计数频数、长时记忆提取效率、优良计算策略频次以及信息加工的变化比率上都显著低于正常组和提高组。因此, 他们主张无提高组、而非提高组儿童才是真正的数学困难儿童。但Geary的鉴别方式至少需要一年的追踪, 才能获得相对可靠的筛查结果,本研究通过增加动态测验施测范式, 在初期鉴别的基础上, 可以几乎同时获得数学困难儿童的潜在发展水平, 并以此作进一步的分类和甄别。

其次, 在S-CPT中最直接反映儿童最近发展区(ZPD)宽度的指标是差异分和稳定分。动态测验的理论是基于 Vygotsky的最近发展区理论而发展起来的, Vygotsky (1978)主张对ZPD的测量是对儿童潜能发展水平的测量。相比较于传统测验, 动态测验的突出特征是不仅测量儿童的当前发展水平, 还能测量其潜在发展水平。本研究中差异分反映了被试加工潜能的宽度或弹性, 稳定分反映被试在没有干预帮助下保持其前期干预所获得的最高水平的能力。研究表明, “发展落后”儿童与正常儿童在差异分和稳定分上没有差异, 且均显示出了较好的认知潜能宽度; 而“发展缺陷”儿童的差异分和稳定分却显著低于前两类儿童。说明“发展落后”儿童与正常儿童的ZPD宽度明显好于“发展缺陷”儿童; ZPD宽度不同或潜能不同的儿童从教学和干预中的获益也不同。

再次, 策略选择与对指导的依赖是动态测验重点考查的内容。策略在数学解题过程中扮演着非常重要的角色, 使用策略的优劣直接决定了数学解题能力。S-CPT策略分显示, “发展落后”与“发展缺陷”儿童使用策略的水平均显著低于正常儿童, 提示这两类儿童之所以在前期学绩测验中无法区分开来,可能是他们都使用了不恰当的解题策略。指导分反映了儿童对提示和帮助的敏感程度, 本研究发现相对于“发展落后”儿童和正常儿童, “发展缺陷”儿童需要更多的提示、帮助和指导。虽然“发展缺陷”儿童较另外两类儿童接受了更多的帮助, 但是其成绩还是落后于这两类儿童, 这是由于“发展缺陷”儿童内化帮助的能力显著低于“发展落后”和正常儿童。所以对于“发展缺陷”儿童来讲, 如要有所增长, 给予正常儿童的帮助量是远远不够的, 家长和教师对他们要有耐心, 在数学学习中要提供足够的、必要的、与之匹配的干预和指导。

最后, 本研究对“发展落后”儿童、“发展缺陷”儿童和正常儿童的三、四年级数学期末考试成绩进行了比较, 发现“发展落后”儿童一年后的数学成绩有了显著改善, 几乎达到了与正常儿童数学成绩一样的程度; 而“发展缺陷”儿童一年后其数学成绩没有提高。与Geary的研究结果(1990, 1991)比较发现,“发展落后”儿童与Geary研究中的“提高组”儿童类似, 而“发展缺陷”儿童与“无提高组”儿童类似。在Geary的研究(1990; 1991)中, 以数学成绩有无提高为标准诊断数学困难儿童历时1年。我们知道, 对数学困难儿童早识别、早发现, 有利于早干预、早见效。采用年级‒水平离差法以学习成绩为指标对数学困难儿童的诊断和甄别的恰当时期是小学四年级, 如果四年级筛查的疑似数学困难儿童要等到5年级才能准确核实确定, 那就不利于早干预的实施。而本研究采用“Swanson认知加工测验”这一标准化的动态测验通过“前测–干预–即时后测–延迟后测”的范式在四年级初就能在传统鉴别方式的基础上几乎同时相对准确地筛查出真正的数学困难儿童, 一来可以降低误报, 避免给低数学成绩儿童贴上“数学学习困难/障碍”的负面标签; 二来及早甄别出有发展缺陷的、真正的数学困难的儿童可以对他们给予恰当适切的干预以减少延误。因此, 与单一传统鉴别方式相比, 结合指向潜能评估的动态测验后, 可以快速、及早地甄别真正的数学困难儿童, 这是对传统筛查方式的有益补充, 也是动态测验的独特的评估优势。

动态测验是基于潜能评估指标进一步区分传统能力测验所筛查出来的特殊群体, 是传统测验的有益补充, 但不脱离和独立于传统测验。近些年,研究者开始探索“数感” (number sense)的涵义、成分和评估方式, 并且发现儿童早期的数感不良是其日后数学困难的强预测变量(Chard, Clarke, Baker,Otterstedt, Braun, & Katz, 2005; Jordan, Glutting, &Ramineni, 2010; Locuniak & Jordan, 2008; Seethaler& Fuchs, 2010)。而数感是个体在学前期就有表现和发展的数学能力, 对这些年幼儿童和低年级儿童数学能力的评估可以指向于对其数感发展水平的测量。当前, 对学习困难鉴别最有突破性的进展是基于动态测验理念发展起来的干预反应范式, 它可以及早发现不同程度的数感不良儿童, 进而及早诊断并及早采取针对性干预。

5 结论

(1)在原有认知能力的基础上, 加入 S-CPT动态测验的“潜在认知能力”指标可以更好地预测儿童的数学成绩, 动态测验是对传统静态测验的有益补充;

(2)“潜在认知能力”指标可以将传统的年级–水平离差法诊断出的数学学习困难儿童进一步区分为“发展落后”儿童和“发展缺陷”儿童; 且“发展落后”儿童、而非“发展缺陷”儿童一年内数学成绩的增长性变化证实了动态测验在快速准确甄别数学困难儿童中的独特作用。

Andrea, S., Elisa, C., Anna, D. S., Susanna, M., Franco, S., &Elisabetta, L. (2006). Central executive system impairment in traumatic brain injury.

Brain Injury,20

(1), 23–32.Butterworth, B. (2008). Developmental dyscalculia. In

Child neuropsychology: Concepts, theory, and practice

(pp.357–374). Malden, MA : Wiley-Blackwell.Bi, Y., & Zhang, L. J. (2014). Good saddle for good horse:Solutions to problems on using ability-achievement discrepancy models to identify mathematical disabilities.

Chinese Journal of Special Education, 14

(5).[毕远, 张丽锦. (2014). 好马还需配好鞍: 以能力-成绩差异模型鉴别数学困难的问题与对策.

中国特殊教育杂志,14

(5).]Bradley, R., Danielson, L., & Hallahan, D. P. (2002).

Identification of learning disabilities

(pp. 374–375).Mahwah, New Jersey: Lawrence Erlbaum Associates.Bull, R., Johnston, R. D., & Roy, J. A. (1999). Exploring the roles of the visual-spatial sketch pad and central executive in children’s with-metical skills: Views from cognition and developmental neuro-psychology.

Developmental Neuropsychology, 15

(3),421–442.Chan, B. M., & Ho, C. S. (2010). The cognitive profile of Chinese children with mathematics difficulties.

Journal of Experimental Child Psychology,107

(3), 260–279.Chard, D. J., Clarke, B., Baker, S., Otterstedt, J., Braun, D., &Katz, R. (2005). Using measures of number sense to screen for difficulties in mathematics: Preliminary findings.

Assessment for Effective Intervention, 30

(2), 3–14.Chong, S. L., & Siegel, L. S. (2008). Stability of computational deficits in math learning disability from second through fifth grades.

Developmental Neuropsychology,33

(3), 300–317.Fernández-Ballesteros, R., Zamarrón, M. D., Tárraga, L.,Moya, R., & Iñiguez, J. (2003). Cognitive plasticity in healthy, mild cognitive impairment (MCI) subjects and Alzheimer's disease patients: A research project in Spain.

European Psychologist,8

(3), 148–159.Haworth, C., Kovas, Y., Harlaar, N., Hayiou‐Thomas, M. E.,Petrill, S. A., Dale, P. S., & Plomin, R. (2009). Generalist genes and learning disabilities: a multivariate genetic analysis of low performance in reading, mathematics,language and general cognitive ability in a sample of 8000 12‐year‐old twins.

Journal of Child Psychology and Psychiatry

(10), 1318–1325.Cornoldi, C., Rigoni, F., Tressoldi, P. E., & Vio, C. (1999).Imagery deficits in nonverbal learning disabilities.

Journal of Learning Disabilities,32

(1), 48–57.Fabio, R. A. (2005). Dynamic assessment of intelligence is a better reply to adaptive behavior and cognitive plasticity.

The Journal of General Psychology, 132

, 41–66.Ferretti, R. P., Butterfield, E. C., Cahn, A., & Kerkman, D. (1992).The classification of children’s knowledge: Development on the balance scale and inclined-plane problems.

Journal of Experimental Child Psychology, 39

, 131–160.Feuerstein, R., Miller, R., Rand, Y., & Jensen, M. R. (1981).Can evolving techniques better measure cognitive change?

The Journal of Special Education, 15

(2), 201–219.Geary, D. C. (1990). A componential analysis of an early learning deficit in mathematics.

Journal of Experimental Child Psychology,49

, 363–383.Geary, D. C., Hoard, M. K., & Hamson, C. O. (1999).Numerical and arithmetical cognition: Patterns of functions and deficits in children at risk mathematical disability.

Journal of Experimental Child Psychology,74

, 213–219.Geary, D. C., Brown, S. C., & Samaranayake, V. A. (1991).Cognitive addition: A short longitudinal study of strategy choice and speed-of-processing differences in normal and mathematically disabled children.

Developmental Psychology,27

(5), 787–797.Geary, D. C., Hamson, C. O., & Hoard, M. K. (2002).Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability.

Journal of Experimental Child Psychology,77

,236–263.Grigorenko, E. L. (2009). Dynamic assessment and response to intervention, two sides of one coin.

Journal of Learning Disabilities,42

(2), 111–132.Haywood, H. C., & Tzuriel, D.(2002). Applications and challenges in dynamic assessment.

Peabody Journal of Education,77

(2), 40–63.Jordan, N. C., Glutting, J., & Ramineni, C. (2010). The importance of number sense to mathematics achievement in first and third grades.

Learning and Individual Differences,20

(1), 82–88.Joni, H., & John, W. A. (2008). The relationship between visuospatial sketchpad capacity and children’s mathematical skills.

European Journal of Cognitive Psychology,20

(2),272–289.Jonides, J., Lacey, S. C., & Nee, D. E. (2005). Process of working memory in mind and brain.

Current Directions in Psychological Science, 14

(1), 2–5.Kimberly, P. R., Marcia, B., & Steven, A. H. (2010). Working memory and mathematics: A review of developmental,individual difference, and cognitive approaches.

Learning and Individual Difference,20

, 110–112.Landerl, K., Fussenegger, B., Moll, K., & Willburger, E.(2009). Dyslexia and dyscalculia: Two learning disorders with different cognitive profiles.

Journal of Experimental Child Psychology, 103

(3), 309–324.Landerl, K., & Kölle, C. (2009). Typical and atypical development of basic numerical skills in elementary school.

Journal of Experimental Child Psychology, 103

(4),546–565.Liu, C. (2005). On working memory in children with mathematics disabilities.

Advances in Psychological Science, 13

(1), 39–47.[刘昌. (2005). 数学学习困难与工作记忆关系研究的现状与前瞻.

心理科学进展,13

(1), 39–47.]Locuniak, M. N., & Jordan, N. C. (2008). Using kindergarten number sense to predict calculation fluency in second grade.

Journal of Learning Disabilities, 41

(5), 451–459.Mabbott, D. J., & Bisanz, J. (2008). Computational skills,working memory, and conceptual knowledge in older children with mathematics learning disabilities.

The Journal of Learning Disabilities,41

(1), 15–28.McLean, J. F., & Hitch, G. J. (1999). Working memory impairments in children with specific arithmetical learning difficulties.

Journal of Experimental Child Psychology, 74

,240–260.Mazzocco, M. M. M., & Meyers, G. E. (2003). Complexities in identifying and defining mathematics learning disability in the primary school-age years.

Annals of Dyslexia, 53

,218–53.Passolunghi, M. C., & Mammarella, I. C. (2011). Selective spatial working memory impairment in a group of children with mathematics learning disabilities and poor problem-solving skills.

Journal of Learning Disabilities,45

(4), 341–350.Passolunghi, M. C., & Siegel, L. S. (2001). Short-term memory, working memory and inhibitory control in children with difficulties in arithmetic problem solving.

Journal of Experimental Child Psychology,80

(1), 44–57.Proctor, B., & Prevatt, F. (2003). Agreement among four models used for diagnosing learning disabilities.

Journal of Learning Disabilities,36

, 459–466.Rasmussen, C., & Bisanz, J. (2010). The relation between mathematics and working memory in young children with fetal alcohol spectrum disorders.

TheJournal of Special Education,45

(3), 184–191.Ravi, N. (2001). Dynamic assessment of graphic symbol combinations by children with autism.

Focus on Autism &Other Developmental Disabilities, 16

, 190–197.Sclan, S. G., Johnson, K., & Haywood, H. C. (1986). Dynamic assessment and thought disorder in paranoid and non-paranoid schizophrenic patients.

George Peabody College for Teachers,74

(2), 54–58.Seethaler, P. M., & Fuchs, L. S. (2010). The predictive utility of kindergarten screening for math difficulty.

Exceptional Children, 77

(1), 37–59.Serge, M. J., Kern, S., Mintz, J., & Green, M. F. (2005).Learning potential and the prediction of work skill acquiring in schizophrenia.

Schizophrenia Bulletin, 31

,67–72.Siegel, S., & Ryan, B. (1989). The development of working memory in normally achieving and subtypes of learning disabled children.

Child Development, 60

, 973–980.Swanson, H. L. (1996).

Swanson-Cognitive Processing Test

.Austin Texan: Pro-Ed.Swanson, H. L., & Howard, C. B. (2005). Children with reading disabilities: Does dynamic assessment help in the classification?

Learning Disability Quarterly, 28

(1), 17–34.Tracy, P. A., Susan, E., Hannah, K., & Julian, E. (2009). The cognitive and behavioral characteristics of children with low working memory.

Child Development,80

(2), 606–621.Tzuriel, D. (1989). Dynamic assessment of learning potential in cognitive education programs.

The Thinking Teacher,5

,1–4.Tzuriel, D., & Klein, P. C. (1985). Analogical thinking modifiability in disadvantaged, regular, special education and mentally retarded children.

Journal of Abnormal Child Psychology,13

, 539–552.Tzuriel, D., & Kaufman, R. (1999). Mediated learning and cognitive modifiability: Dynamic assessment of young Ethiopian immigrants in Israel.

Journal of Cross-Cultural Psychology,30

, 359–380.Vygotsky, L. S. (1978).

Mind in society

. Cambridge, MA:Harvard University Press.Wang, E. G., Liu, C., & Zhao, G. X. (2008). Processing speed and working memory in children with mathematical disabilities.

Psychological Science, 31

(4), 856–860.[王恩国, 刘昌, 赵国祥. (2008). 数学学习困难儿童的加工速度与工作记忆.

心理科学,31

(4), 856–860.]Zhang, H. C., & Wang, X. P. (1985).

Raven's Standard Progressive Matrices

. Beijing: Beijing Normal University Press.

[张厚粲, 王晓平. (1985). 瑞文标准推理测验. 北京: 北京师范大学出版社.]

Zhang, L. J., Chen, L., & Fang, F. X. (2011). The adaptation of dynamic test using the Inventory of Piaget’s Developmental Task (IPDT): An initial validation and application.

Acta Psychologica Sinica, 43

(9), 1075–1086.[张丽锦, 陈亮, 方富熹. (2011). “儿童认知发展水平诊断工具”动态测验的初步编制与应用.

心理学报, 43

(9),1075–1086.]Zhang, L. J., Gai, X. S., Fang, F. X., & Fang, G. (2003).Dynamic assessments of children’s cognitive development.

Chinese Journal of Special Education, 11

, 651–657.[张丽锦, 盖笑松, 方富熹, 方格. (2003). 儿童认知发展动态测验.

心理科学进展,11

, 651–657.]Zhu, L. Q. (1999). Cognitive features of mathematics learning disabilities solving simple math addition and subtraction.

Chinese Journal of Special Education, 23

(3), 34–45.[朱莉琪. (1999). 数学学习困难儿童解决简单加减法的认知特点的实验研究.

中国特殊教育,23

(3), 34–45.]