随机PRI的LPI波形相参积累
李 斌,黄银和,吴 刚,雷志勇
(南京电子技术研究所,南京 210039)
1 引 言
现代脉冲多普勒(PD)雷达面临来自电子支援措施(ESM)系统的威胁。ESM对辐射源测量电子参数(方向、重频、脉宽等)进行分选、配对,形成完整的辐射源描述字。电子对抗装置(ECM)据此配置干扰策略以对抗PD雷达的探测。
脉冲重复频率(PRI)是雷达辐射源电子参数的关键特征。PRI参差滑变时,ESM系统无法通过重频实现对脉冲辐射源配对,这增加了电子战系统侦察、截获、测量、分析、识别的复杂程度。因此,随机PRI脉冲波形能够有效提升PD雷达复杂电磁环境下的对抗能力。然而,随机PRI脉冲波形在实际应用中面临如下问题:一是针对随机PRI脉冲波形,非均匀离散傅里叶变换(NUDFT)算法在距离模糊条件下导致目标能量分散至多个模糊距离单元,检测概率降低;二是随机PRI脉冲回波在时域上是非均匀采样,使用均匀窗函数无法有效抑制目标多普勒副瓣[1]。
一些学者对随机PRI波形在雷达中的应用进行了相关研究。Mark W.Maier[1]提出NUDFT算法解决了无距离模糊条件下目标能量的相参积累。M.Modarres-Hashemi等[2]通过分析随机PRI雷达信号的低检测概率(LPD)性能,指出随机PRI信号与周期信号相比具有更高的安全性。Jen-tsai K[3-4]等采用不同的插值和优化准则发展了非均匀快速傅里叶变换(NUFFT),有效提高NUDFT算法的运算速度。Juan Li[5]等人对比了NUDFT和NUFFT在运算量和测量精度方面的性能差异,指出NUFFT算法的运算量优于NUDFT算法。刘振[6]等研究了在目标距离和速度都不模糊的情况下随机PRI脉冲雷达的动目标检测技术,部分解决了传统算法中的粗糙损失和杂波抑制问题。罗长胜[7]等将脉冲相似度引入随机PRI脉冲信号的分选,取得95%以上的分选准确率。
本文针对具有低截获概率(LPI)性能的随机PRI脉冲波形,提出一种目标能量相参积累算法——TWDFT(Time Window DFT)算法,通过在相干处理间隔(CPI)内抽取相参脉冲片段,实现距离模糊条件下目标能量的相参积累。最后,本文仿真分析了随机PRI脉冲波形的加权副瓣抑制性能,指出优化波形设计能够改善加权后目标主副瓣比。
2 随机PRI脉冲信号
发射相参脉冲串信号s(t)有M个时宽为tp的线性频率调制脉冲,每个脉冲的起始时刻为tt(m)(m=1,2,…,M),则随机PRI脉冲发射信号表示为
(1)
其中,线性频率调制的中心频率为零,A是脉冲信号幅度,B是脉冲信号调制带宽,矩形脉冲信号为
(2)
起始时间tt(m)表示为(m=1,2,…,M):
(3)
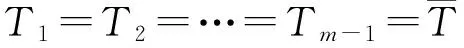
假设目标时延为τ,多普勒频移为fd,传输功率损耗为L,则回波信号为
(4)
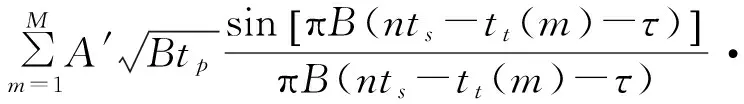
exp(j2πfdtt(m)),n=1,2,3…
(5)
第m个子脉冲、第k个距离门的目标响应表示为

exp(j2πfdtt(n)),m=1,2,…,M
(6)
距离门k满足条件tt(m)+kts+tp≤tt(m+1)。
3 基于NUDFT算法的相参积累
3.1 基本原理
随机PRI脉冲发射信号的回波数据是非均匀的,使用离散傅里叶变换进行相参积累的表达式为
(7)
其中,f表示测试频率,一个CPI内的回波脉冲数为M。公式(7)定义了 NUDFT 算法。
第m个发射脉冲在第l个脉冲接收周期内返回,它在当前接收周期上的时间延迟为Rt。时延为τ的目标在无距离模糊时满足l=m、Rt=τ。设目标所处距离门为kt:ktts+tp=Rt=τ,则
(8)
如果只取sinc函数的主瓣,目标距离门kt处的相参积累结果表示为
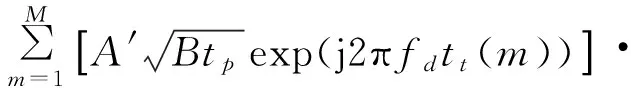
exp(-j2πftt(m))
(9)

3.2 距离模糊
定义回波脉冲的模糊重数为C(m)(m=1,2,…,M,C(m)=0,1,2,…),C(m)等于0表示无距离模糊。目标回波脉冲位置表示为
(10)
其中,D(m)满足
(11)
目标所处距离门kt满足ktts+tp=Rt=τ-D(m),则
(12)
其中,kt的取值由目标时延τ和发射波形PRI的取值决定。有距离模糊时,kt随回波脉冲的变化而变化,导致NUDFT处理后目标能量分散到多个模糊距离单元,信杂噪比降低。
4 基于TWDFT算法的相参积累
4.1 基本原理
本文设计了一种改进的相参积累算法,能够消除距离模糊中目标所处距离门kt随回波脉冲的变化(如图 1所示)。设时间窗口的距离门延迟量是kd,第m(m=1,2,…,M)回波脉冲的时间窗口起始时间tb(m)表示为:tb(m)=tt(m)+tp+kdts。设一次相参处理的期望观测距离为L,则时间窗口的宽度tlen可确定为tlen=2L/c,其中c是电磁波传播速度。一组固定的kd和tlen取值可确定M个时间窗口。利用这M个时间窗口进行接下来的TWDFT运算,如果没有观测到相参目标回波,就增加kd的取值重新进行计算。这一滑动迭代过程直到发现目标信号或tb(m)相对tt(m)足够大(可以确定没有目标回波信号)为止。
对于一组固定的kd和tlen,可以将其确定的M个时间窗口组合成矩阵形式:
(13)

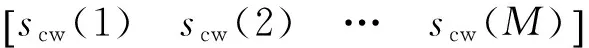
(14)
scw(m)=w(m)scR(n)=
n=0,1,2,…
(15)
假设当前时间窗口组中包含相参目标回波,将公式(5)代入公式(15),对确定的时间窗口,第m个回波脉冲、第kl个距离门的回波采样数据表示为
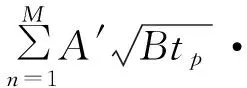
exp(j2πfdtt(n))
(16)
其中,kl=1,2,…,tlen/ts。当kd=0、tlen=(tt(m+1)-tt(m)-tp)/ts时,公式(16)所示回波采样数据与公式(6)等价。
对相同距离门的scw[m,kl]进行DFT变换,则相参积累的结果Ycw(f)表示为

(17)
其中,
(18)
其中,kl=1,2,…,tlen/ts。公式(18)定义了时间窗口离散傅里叶变换(TWDFT)算法。
对包含相参目标回波的时间窗口,目标所处距离门kt满足ktts+tp+kdts=τ,则
(19)
其中,kt的取值由目标时延τ和时间窗口距离门延迟量kd决定。当kd固定时,M个时间窗口中的目标响应在距离门上对齐且彼此相参,使用公式(19)后可获得最大积累增益。
4.2 目标参数的补偿
使用TWDFT算法时,时间窗口在距离门上滑动,距离-多普勒谱上获得的目标距离发生偏移。可以通过在距离测量值上累加时间窗口的延迟量,实现对距离偏移的补偿。TWDFT处理后目标所处距离门为kt,多普勒频率为ft,则目标的真实距离R和多普勒速度v为
(20)
其中,c为雷达发射脉冲的传播速度,ts为雷达接收机的采样周期,λ为雷达发射脉冲的发射波长,kd为相应时间窗口在距离门上的延迟量。
4.3 降低副瓣的加权方法
PD雷达中,相参积累算法通过在各个子脉冲上加权实现对目标多普勒副瓣的抑制。设加权系数为wd(m)(m=1,2,…,M),使用TWDFT算法进行加权相参积累的过程表示为
(21)

ycw(n,kl)=FFT[wd(m)sn[m,kl]exp(j2πtbΔ(m)(fd-f))]
(22)
其中,FFT[·]表示M点快速傅里叶变换。
根据公式(22),目标主瓣峰值处f等于fd,峰值大小与信号PRI的取值(即tbΔ(m))无关;目标副瓣区f与fd存在差异,副瓣电平随相位差2πtbΔ(m)(fd-f)的变化而变化。因此,目标主副瓣比(MSR)不仅受限于加权深度,而且与发射信号PRI的取值分布有关。通过随机PRI脉冲波形的优化设计可以获得优良的目标MSR。波形设计问题将另文讨论。
5 仿真与分析
5.1 相参积累性能

假设平均PRF为300 Hz,平均PRI约为3.33 ms,无距离模糊,B为2 MHz,fs为3 MHz,目标fd取100 Hz,SNR为0,σ=0.2,不加窗。仿真结果见图2,可见无距离模糊时NUDFT算法与TWDFT算法性能等价,可准确测得目标速度和距离,无相参积累增益损失。
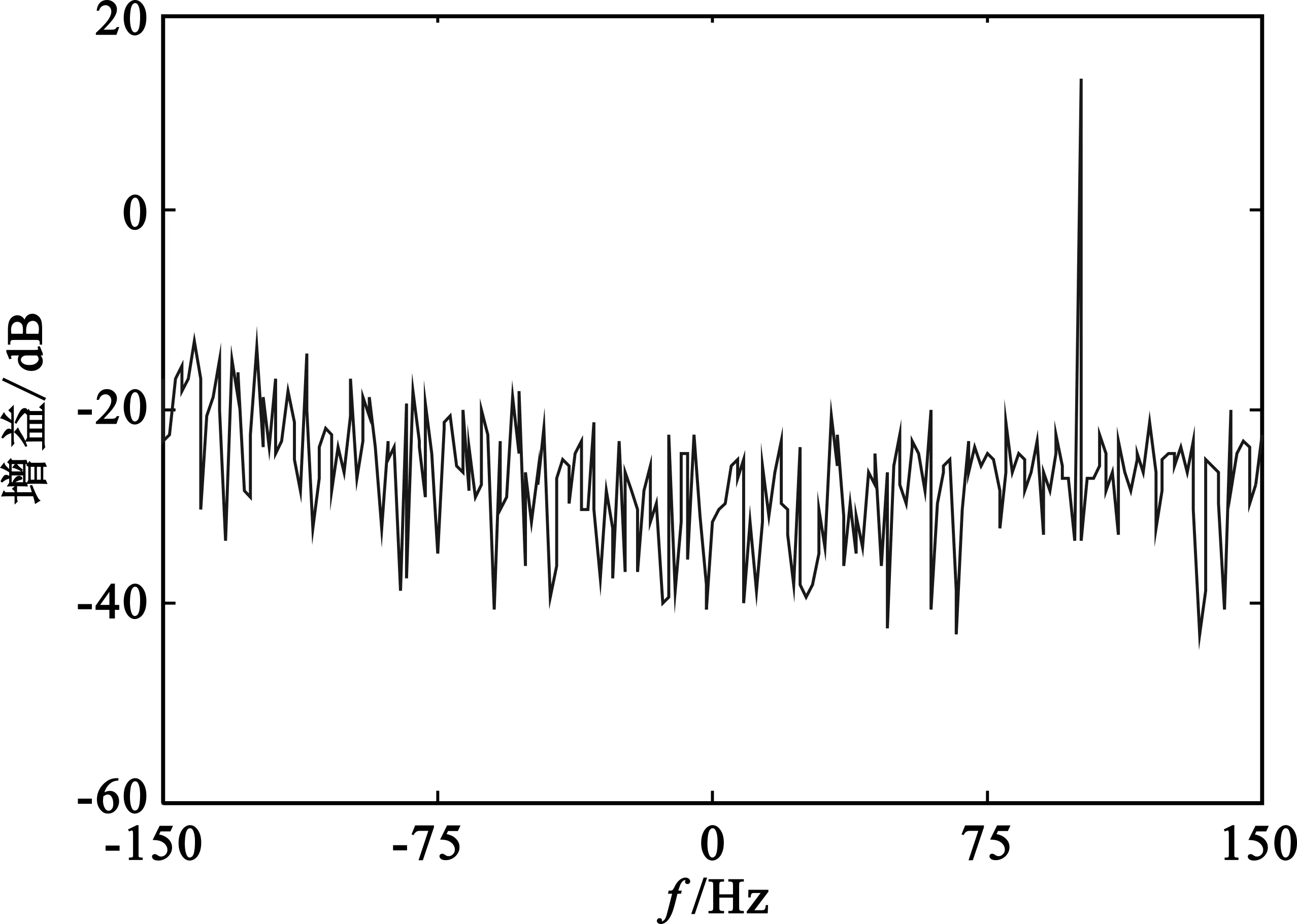
(a)NUDFT
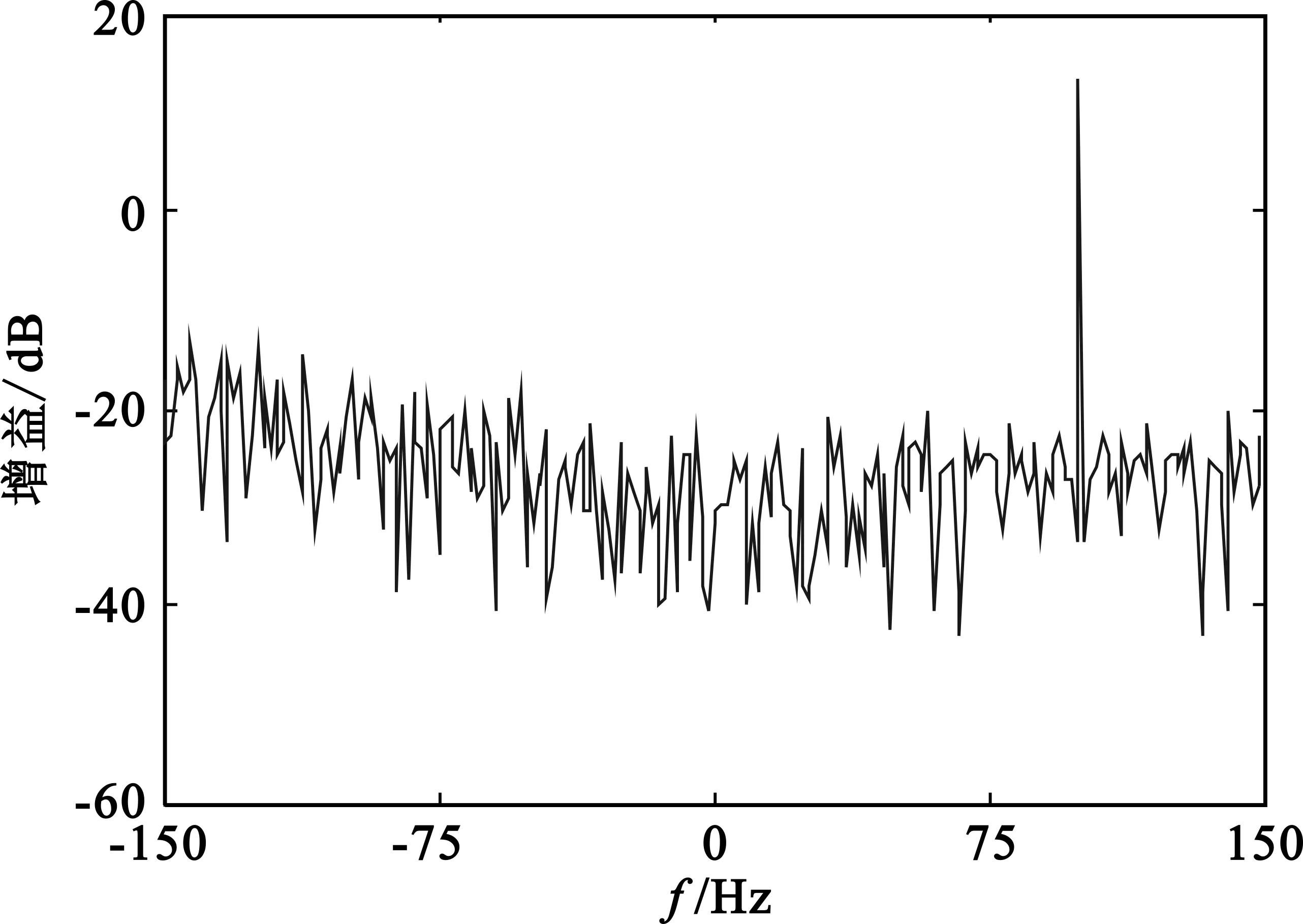
(b)TWDFT
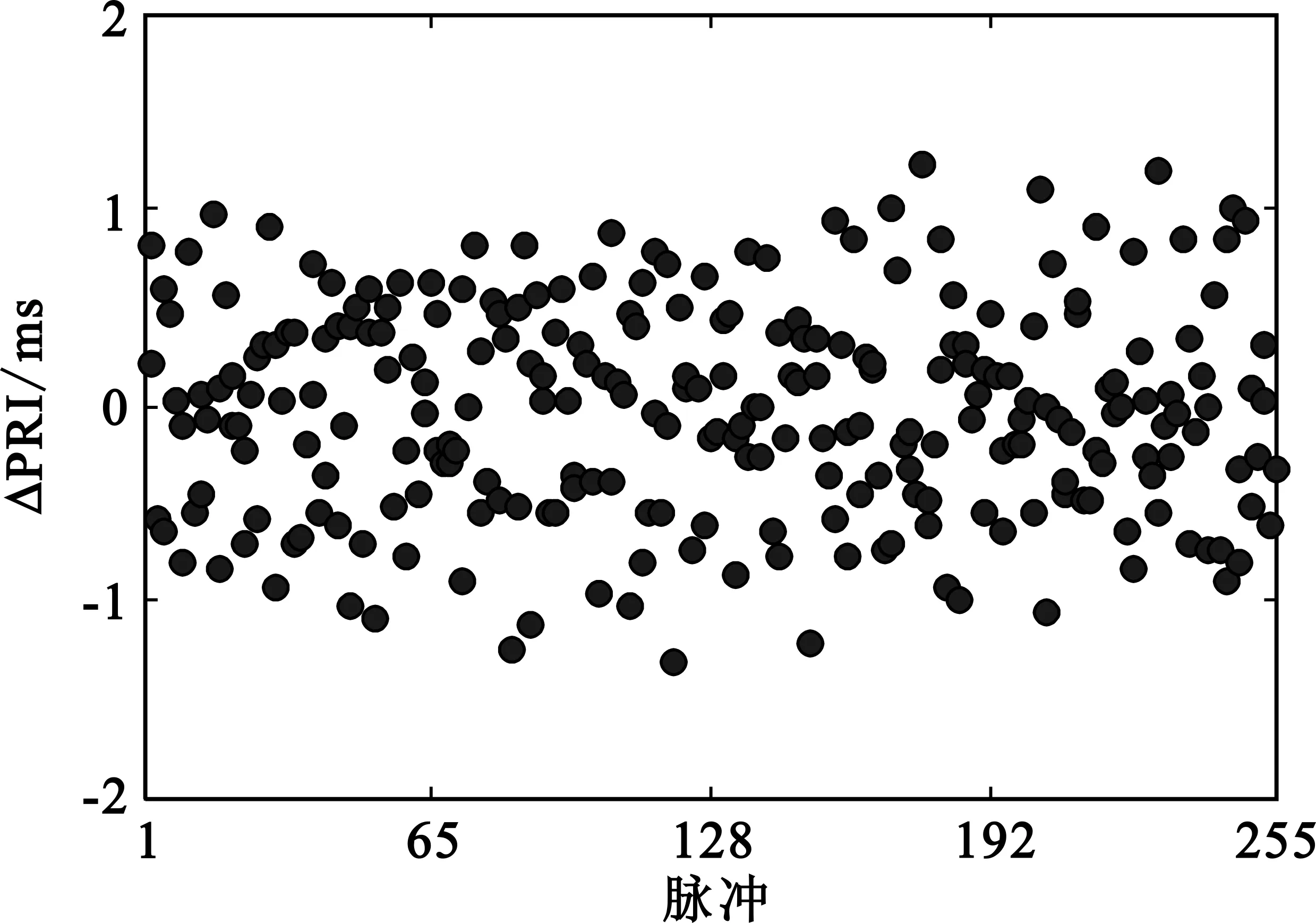
(c)发射信号相邻PRI之差图2 无距离模糊、随机PRI脉冲信号的相参积累Fig.2 The coherent accumulation of random PRI pulse waveform without range ambiguity
假设平均PRF为1 500 Hz,平均PRI约为0.667 ms,存在距离模糊,其他仿真条件不变。仿真结果见图3,可见距离模糊时,NUDFT算法无法实现目标参数的测量;TWDFT算法能够实现目标能量的相参积累,准确测量目标速度和距离。
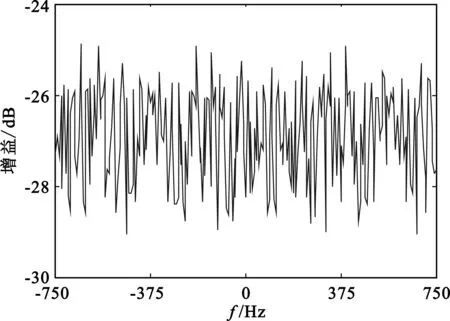
(a)NUDFT
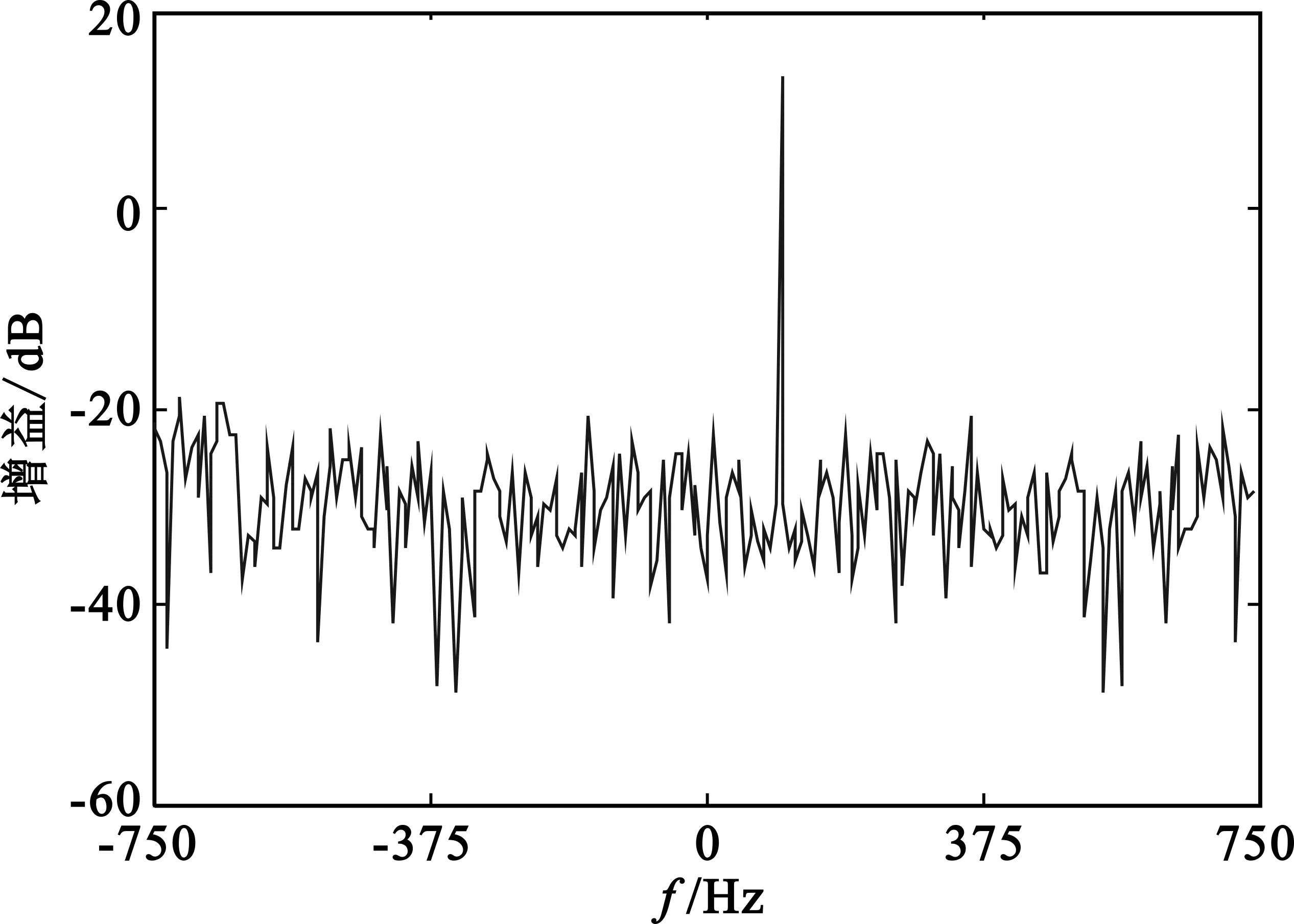
(b)TWDFT
5.2 加权降低副瓣
本节通过仿真数据,分析加权深度与发射脉冲PRI取值在TWDFT算法中对副瓣抑制性能(目标MSR)的影响。假设无距离模糊,目标fd取100 Hz,使用4种不同发射脉冲信号进行仿真,其中σ=0.1的随机PRI信号任取两组不同PRI取值。仿真结果见图4,可见目标的MSR随加权深度增加而增加;加权深度确定时,波形的PRI变化会导致目标MSR变化。从仿真结果可见,加权深度为40 dB时,对应于σ=0.1、第1组PRI取值的脉冲信号,目标MSR为40.64 dB,即存在特定PRI取值使目标MSR优于加权深度。因此,通过优化波形设计能够改善加权后目标MSR。上述仿真结果验证了4.3节的理论分析。
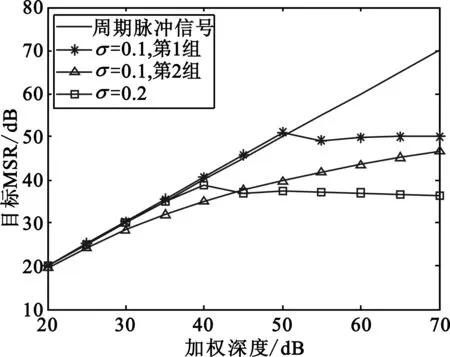
图4 目标MSR的变化Fig.4 The change of target MSR
6 结束语
使用NUDFT算法对随机PRI脉冲波形进行脉冲多普勒处理时,距离模糊引起目标所处距离门走动,导致目标能量分散至多个模糊距离单元;同时,随机PRI脉冲波形会导致均匀窗函数的旁瓣抑制性能下降。针对这些问题,本文首先提出TWDFT算法,通过时间窗口在CPI内滑动搜索相参脉冲信号,实现了距离模糊条件下目标能量的相参积累;其次,仿真分析了TWDFT算法的加权副瓣抑制性能,指出通过优化波形设计能够改善加权后目标主副瓣比。本文提出的算法和思路使随机PRI脉冲波形能有效应用于现代PD雷达体制,改善雷达复杂对抗环境下的抗侦收能力。对加权后目标MSR的仿真结果表明,不同的脉冲波形参数会造成加权后目标主副瓣比的起伏,故需要进一步研究随机PRI脉冲波形参数的设计和优化问题。
[1] Maier M W.Non-uniform PRI pulse-Doppler radar[C]//Proceedings of Twenty-Fifth Southeastern Symposium on System Theory.Tuscaloosa,AL:IEEE,1993:164-168.
[2] Modarres-hashemi M,Nayebi M M.LPD feature improvement in radom PRF radar signals[J].IEE Proceedings—Radar,Sonar and Navigation,2004,151(4):225-230.
[3] Jen-tsai K,Hsin-ying L.Improved Accuracy Factors for the Nonuniform Fast Fourier Transform(NUFFT) Algorithm[J].IEEE Microwave and Wireless Components Letters,2009,19(1):3-5.
[4] Jacob M.Optimized Least-Square Nonuniform Fast Fourier Transform[J].IEEE Transactions on Signal Processing,2009,57(6):2165-2177.
[5] Li Juan,Chen Zhuming.Research on Radom PRI PD radar target velocity estimate based on NUFFT[C]// Proceedings of 2011 IEEE CIE International Conference on Radar.Chengdu:IEEE,2011:1801-1803.
[6] 刘振,魏玺章,黎湘,等.基于改进CS的随机PRI雷达精确测速及杂波抑制算法[J].国防科技大学学报,2013,35(3):114-118.
LIU Zhen,WEI Xi-zhang,LI Xiang,et al.Precise velocity measurement and clutter suppression in random pulse repetition interval radar based on improved compressed sensing[J].Journal of National University of Defense Technology,2013,35(3):114-118.(in Chinese)
[7] 罗长胜,吴华,程嗣怡.一种对重频调制与抖动信号的PRI变换分选新方法[J].电讯技术,2012,52(9):1492-1496.
LUO Chang-sheng,WU Hua,CHENG Si-yi.A New Method for Sorting PRI Modulated and Jittered Pulse Signal Based on PRI Transformation[J].Telecommunication Engineering,2012,52(9):1492-1496.(in Chinese)

