一种最小冗余线阵的目标DOA估计方法

胡子扬，任 渊

(中国船舶重工集团公司第七二四研究所，南京 211106)

1 引 言

在现代阵列信号处理领域，波达方向(DOA)估计是一个重要的研究方向，占有重要地位。在DOA估计中，均匀线阵(Uniform Linear Array,ULA)因其结构简单在实际系统中得到广泛应用。一般而言，阵元数一经确定，均匀线阵的阵列分辨率就确定了，只能通过增加阵元数目或增加阵元间距来提高分辨率。增加阵元数目会增加设备量，这将对信号处理量以及通道误差调节和系统可靠性都带来影响；而过大的阵元间距会引起栅瓣效应，使DOA估计出现模糊。因此在工程实践中，采用非均匀阵列来节省设备量，提高估计精度成为研究的热点，很多学者对非均匀阵列进行了大量研究[1-4]。使用非均匀阵列可以利用较少的阵元得到较大的天线孔径，为了防止栅瓣的出现，要求非均匀阵列阵元距参考阵元的归一化间距互质。实验证明，这种非均匀阵列有其优势，但并非最优阵列，相同的孔径下其阵元数可进一步减少。同时，学者们也对给定阵元数下所能达到最大孔径的最小冗余线阵(Minimum redundancy linear array)进行了大量研究[5-7]，但最小冗余线阵的排布方式固定，不适用于相干信源的DOA估计，又给工程应用带来了不便。

本文从孔径合成理论出发，在最小冗余线阵的基础上，通过对其阵元位置及个数进行优化设置，在相同的孔径条件下，得到比一般非均匀线阵阵元数更少、比最小冗余线阵阵元选择更灵活的次最小冗余线阵，同时解决了最小冗余线阵不能处理相干目标的问题，更有利于工程应用。

2 次最小冗余线阵及其数学模型

2.1 非均匀线阵阵列模型

如图1所示，设一个非均匀线阵，由M个阵元组成，以左边第一个阵元为参考阵元，阵元的位置分别为D=(d1,d2,…,dM)，P个波长为λ的窄带平面波，分别从(θ1,θ2,…,θP)入射，第i个阵元收到的信号为

(1)

式中，d1=0,Sm(t)是接收的第m个信号的复包络,ni是第i个阵元接收到的加性噪声。

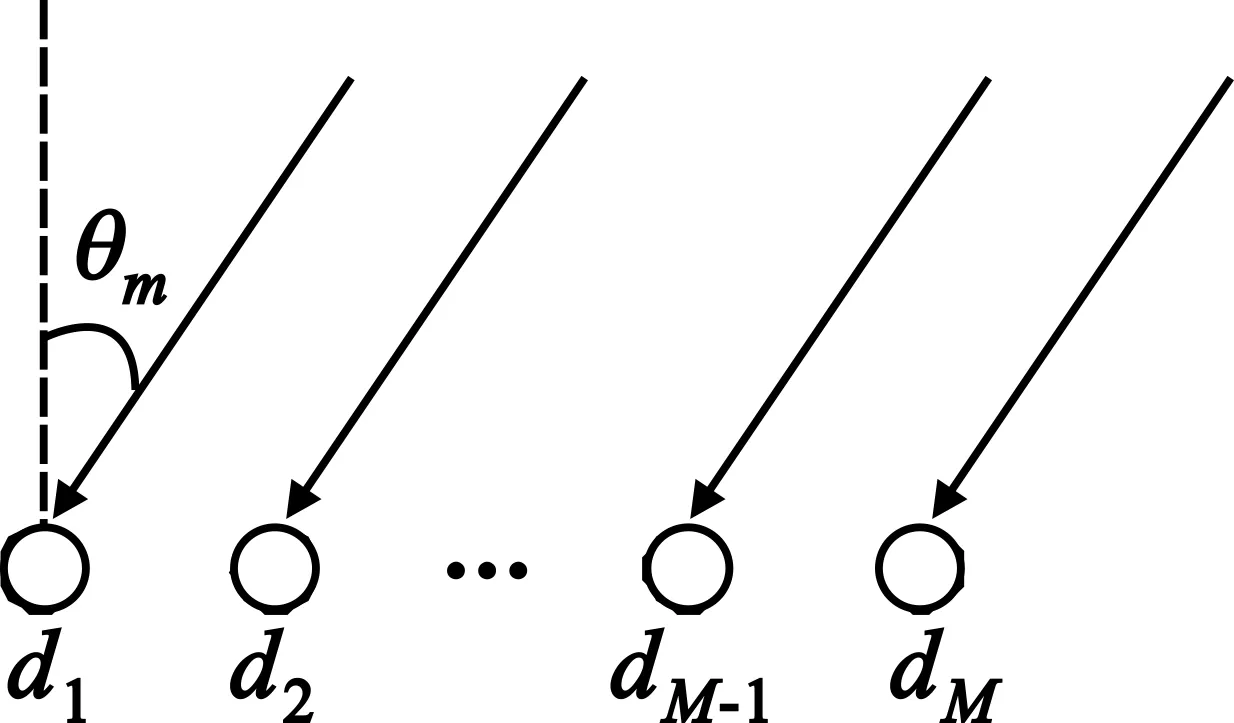
图1 非均匀直线阵测向基本模型Fig.1 The basic model of direction-finding for non-uniform linear array

将式(1)表示成向量形式：

X(t)=A(θ)S(t)+N(t)

(2)

式中，X(t)为阵列输出向量,S(t)为接收的信号向量,N(t)为接收的噪声向量。

定义A(θ)=[a(θ1),a(θ2),…,a(θP)]为方向向量a(θi)构成的阵列流形，其中i=1,2,…,P。记k=2π/λ，则信号在θi方向上的方向向量a(θi)可以表示成

a(θi)=[1,exp(jkd2sin(θi)),…,exp(jkdMsin(θi))]T

(3)

2.2 次最小冗余线阵

由上一节的分析，考虑线阵中任意两个阵元p和q输出的共轭循环相关函数[6]

(4)

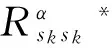
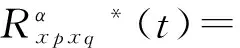
(5)

从式(5)中可以看出对于非均匀线阵，其共轭循环相关函数仅只与dp和dq有关。根据孔径合成理论的叠加等价阵列的定义[8]，阵列A的叠加等价阵列表达式为

Csum(A)={di+dj,1≤i,j≤M}

(6)

式(6)表示di+dj所有可能值表示的集合。若阵列A与阵列B等价即Csum(A)=Csum(B)，则两阵列有相同的孔径。由式(6)可以看出均匀线阵不同的阵元组合可以获得相同的共轭循环相关函数值，因而带来冗余度。

由上面的理论分析，可以设计共轭循环相关函数值重复最少，也即冗余度最小的阵列，称之为最小冗余线阵。最小冗余线阵的设计是一个优化问题，一般通过计算机穷尽搜索的办法获得。表1给出了其中一种不同阵元数的归一化配置[9]，其中M表示阵元数，N表示孔径，{di}中整数表示各阵元相对于第一个阵元距离对半波长的归一化值。

表1 最小冗余线阵归一化配置Table 1 The normalized configuration of minimum redundancy linear array

显而易见，最小冗余线阵的排布是通过穷举法得来的，其阵元排布方式即使不唯一也不能随意更改。同时由表1可以看到，基本上最小冗余线阵都是空间非对称的，而后面我们将分析空间非对称线阵不适用于修正MUSIC算法估计相干信源。当估计相干信源或最小冗余线阵中某一个阵元的通道误差过大时，就需要对其进行修改构成新的冗余度稍大的等价线阵，称之为次最小冗余线阵。

(1)估计相干信源需要按照穷举法设计空间对称的次最小冗余线阵；

(2)应对通道误差较大的阵元则是在阵列等价前提下用其附近的阵元来替换该阵元。如本文中MUSIC算法的仿真使用的是8元最小冗余线阵{0,1,4,10,16,18,21,23}修改后的次最小冗余线阵{0,1,4,7,11,12,13,16,18,21,23}，两者阵列是等价的。

3 次最小冗余线阵的DOA估计算法

3.1 MUSIC算法[9]

多重信号分类(MUSIC)算法作为一种解自相关矩阵特征空间的子空间类算法，它不限于阵列的排列形式，所以MUSIC算法很适合次最小冗余线阵的DOA估计。

由式(2)的信号模型，对阵列信号X(t)的协方差矩阵R=E[X(t)XH(t)]进行特征分解，有

(7)

式中，Us是由大特征值对应的特征矢量张成的信号子空间，而UN是由小特征值对应的特征矢量张成的噪声子空间。

MUSIC算法的谱估计公式为

(8)

对于次最小冗余线阵，在利用MUSIC算法进行DOA估计时，式(8)的表达式是不变的，只是a(θ)，UN受次最小冗余线阵阵元位置di的影响，即阵元位置影响了算法的性能。

3.2 修正MUSIC算法[10]

修正MUSIC(MMUSIC)算法在进行正常非相关信源DOA估计的同时，可以提高对相关信源的估计性能。

修正MUSIC算法对数据协方差矩阵R=E[X(t)XH(t)]进行修正，令Iv为M×M的反向单位矩阵，即

(9)

且令

RX=R+IvR*Iv

(10)

式中，R*为R的共轭，对RX进行如上MUSIC算法就可以得到信号的DOA估计。

修正MUSIC算法估计数据协方差矩阵时，将接收数据共轭重排后再用了一次，这就要求共轭重排后的数据与原数据具有很强的互补性关系，从而利用它们共同估计数据协方差矩阵以改善DOA估计性能，也即满足对称布阵，就是要求构建阵元关于线阵中点对称分布的等价阵列。表2给出了一些空间对称布阵的次最小冗余线阵的归一化配置[11]。

表2 空间对称次最小冗余线阵归一化配置Table 2 The normalized configuration of space symmetrical sub-minimum redundancy linear array

4 仿真实验

使用最小阵元间隔为d=λ/2的线阵，所用噪声为加性高斯白噪声。

4.1 MUSIC算法仿真

(1)实验1:几种线阵MUSIC算法性能分析

实验中设置信号是频率为f0的调幅信号，采样率为2f0，快拍数为200，不考虑通道误差。不失一般性，取仿真的次最小冗余线阵为{0,1,4,11,12,13,16,18,21,23}，它是一个口径同样为24的最小冗余线阵{0,1,4,10,16,18,21,23}修改得到的。在信噪比为10 dB时仿真了这两个线阵和8元及24元均匀线阵对入射方向为(7°,10°,30°,70°)的4个独立入射信号的DOA估计结果，如图2所示。

图2 MUSIC算法仿真结果Fig.2 Simulation results of MUSIC algorithm

从图2可以看出，同样作为8阵元线阵，均匀线阵的分辨力明显不如最小冗余线阵和次最小冗余线阵(10阵元)，3°内的两个信源出现谱峰兼并，已分辨不出来。由(b)、(c)、(d)可以看出，阵列孔径相同的24元均匀线阵、最小冗余线阵和次最小冗余线阵均可以分辨3°以内的目标，最小冗余线阵效果略差一点。最小冗余线阵和次最小冗余线阵的谱函数图像略有起伏，但不影响分辨结果。图3是在不同信噪比下4种线阵对30°入射信号DOA估计的均方根误差曲线。

图3 均方根误差随信噪比变化曲线Fig.3 The change curve of the root mean square error for different SNR

从图3可以看出，孔径较小的8元均匀线阵在信噪比为-5 dB时的均方根误差较之其他3种线阵有明显开始变大的趋势，而孔径相同的3种线阵在信噪比大于-10 dB时的均方根误差相差不大。

(2)实验2:对独立信号的分辨率和估计精度

在MUSIC谱峰搜索中，当两独立信号角度间隔靠近时，会出现谱峰兼并，同时也影响两信号的DOA估计准确度，验证线阵对两角度间隔很近的信号的分辨能力是很有必要的。定义：如果两信号的估计误差在0.3°以内并且两峰值与其之间谷值相差大于5 dB，则认为成功分辨，否则不能分辨。在信噪比10 dB下，对不同入射间隔的两独立信号进行估计，得到图4所示的不同角度间隔下的分辨概率，每个角度间隔进行1 000次独立实验。

图4 不同角度间隔下的分辨概率Fig.4 Resolution probability under different angle interval

从图4可以看出，孔径较小的8阵元均匀线阵对非相干信号具有较差的分辨率，当角度间隔小于3°时，分辨概率就低于90%；其余3个线阵具有较好分辨率，能分辨间隔1°的两个信号。综合来看，次最小冗余线阵在提高分辨力和降低计算复杂度方面有较好的效果。

4.2 MMUSIC算法仿真

实验中仍设置信源数N=4，入射角度为(10°,20°,30°,70°)，信噪比为10 dB，设置其中角度为10°和20°的两个入射信号为全相干信号。由前面分析知，对相干信号的DOA估计需要空间对称线阵，取仿真的空间对称次最小冗余线阵为{0,1,4,7,11,15,18,21,22}，它也是最小冗余线阵{0,1,4,10,16,18,21,23}修改得到的，不过考虑要满足空间对称性，损失了一个阵元的孔径。这两个线阵及8元和24元均匀线阵的DOA估计结果如图5所示。

图5 MMUSIC算法仿真结果Fig.5 Simulation results of MMUSIC algorithm

从图5可以看出，不具有空间对称性的最小冗余线阵{0 1 4 10 16 18 21 23}对相干信号的估计已经失效，而具有空间对称性的另外3个线阵对相关信号的估计性能良好，同时不影响其中非相干信号的估计。用该3种线阵对相干信号进行估计精度分析，得到图6。

图6 对相干信号不同角度间隔下的分辨概率Fig.6 Resolution probability for coherent signals under different angle interval

从图4和图6的比较可以看出，相干信号之间是互相有影响的，表现到分辨率中就是使每个线阵的分辨率变差，如24元均匀线阵分辨概率大于90%的角度间隔提升到1.25°，但总体的规律保持不变，具有相近孔径的次最小冗余线阵和24元均匀线阵的分辨率相差不大，优于具有较小孔径的8元均匀线阵。

整体仿真结果表明，空间对称次最小冗余线阵适用于对相干信号的DOA估计，解决了最小冗余线阵在该方面的不足。

5 结 论

本文针对所提出的次最小冗余线阵DOA估计，给出了分析和实验仿真，结果表明MUSIC等子空间类算法适用于次最小冗余线阵，同时与一般的阵列排布方法相比，次最小冗余线阵具有极大的灵活性，可以灵活选择阵元，避免误差较大的通道；同时在保证阵列孔径和分辨力的前提下，可有效降低阵元数量和算法复杂度，在相关信源的DOA估计中也具有良好的效果。但次最小冗余线阵因其阵元选择的灵活性带来阵列的不固定性，替代较大误差通道的阵元选择的优先级顺序及所带来的影响有待进一步研究，同时空间对称次最小冗余线阵的阵元选择方式也需进一步明确。

[1] 牟建明.基于非均匀线阵的空间谱估计测向算法研究[D].南京:南京理工大学,2005.

MOU Jian-ming.Study on the spatial spectral estimation direction finding algorithm based on non-uniform linear array[D].Nanjing:Nanjing University of Science and Technology,2005.(in Chinese)

[2] 邵丽君,赵淑青.一种优化非均匀阵列天线测向性能的方法[J].电讯技术,2005,45(2):116-119.

SHAO Li-jun,ZHAO Shu-qing.A method to improve the performance of estimating direction-of-arrival in nonuniform linear antenna array[J].Telecommunication Engineering,2005,45(2):116-119.(in Chinese)

[3] 王鹏,张国军,熊继军.非均匀矢量阵列的定向性能仿真与分析[J].计算机仿真,2011(4):388-392.

WANG Peng,ZHANG Guo-jun,XIONG Ji-jun.Performanc simulation and analysis of DOA estimation based on non-uniform vector array[J].Comuputer Simulation,2011(4):388-392.(in Chinese)

[4] 李胜红.非均匀阵高精度测向技术研究[D].成都：电子科技大学,2013.

LI Sheng-hong.Research on non-uniform array high accuracy of techiniques[D].Chengdu:University of Electronic Science and Technology of China,2013.(in Chinese)

[5] 张利强,全厚德.最小冗余线阵的DOA估计[J].火力与指挥控制,2012(10):10-13.

ZHANG Li-qiang,QUAN Hou-de.A study on DOA estimation of minimum redundancy linear array[J].Fire Control and Command Control,2012(10):10-13.(in Chinese)

[6] 崔波,罗景青.最小冗余线阵的ES-DOA估计算法研究[J].信号处理,2010,26(7):1016-1020.

CUI Bo,LUO Jing-qing.Study on ES-DOA estimation algorithm of minimum-redundancy linear arrays[J].Signal Processing,2010,26(7):1016-1020.(in Chinese)

[7] 李磊,祁德元,路翠华.基于约束最小冗余线阵与干扰对消的测向方法[J].海军航空工程学院学报,2013,28(4):383-388.

LI lei,QI De-yuan,LU Cui-hua.Direction finding based on restricted minimum redundant linear arrays and interference canallation[J].Journal of Naval Aeronautical and Astronautical,2013,28(4):383-388.(in Chinese)

[8] 姚敏立,金梁,殷勤业.一种基于最小冗余线阵的时空共轭循环谱相关ESPRIT算法[J].电子科学学刊,2000,22(1):35-41.

YAO Min-li,JIN Liang,YIN Qin-ye.A temporo-spatial conjugate cyclic ESPRIT spectrum correlation algorithm with minimum-redundancy linear array[J].Journal of Electronics,2000,22(1):35-41.(in Chinese)

[9] Moffet A.Minimum-redundancy linear arrays[J].IEEE Transactions on Antennas and Propagation,1968,16(2):172-175.

[10] Debasis K.Modified MUSIC algorithm for estimating DOA of signals[J].Signal Processing,1996(8):111-114.

[11] 张西托,饶伟,胡冬梅,等.基于非均匀线阵和修正MUSIC算法的DOA估计[J].火力与指挥控制,2009(增1):35-36+40.

ZHANG Xi-tuo,RAO Wei,HU Dong-mei,et al.DOA estimation based on nonuniform linear array and modified MUSIC algorithm[J].Fire Control and Command Control,2009(S1):35-36+40.(in Chinese)