贵州省高校体育教师胜任力评价指标体系的构建

田 广，高 徐，张 龙 ，么广会，彭 杰，田 江，田 密

根据《学校体育工作条例》[1]《全国普通高等学校体育课程教学指导纲要》[2]的通知精神，“体育教师应当热爱学校体育工作，具有良好的思想品德、文化素养，体育教师是课程教学的具体执行者和组织者。体育教师要与时俱进，努力提高自身的政治、业务素养。”可以看出，国家对体育教师的要求有明确的规定。笔者以新课改为背景，以体育教师的胜任力为核心，以体育课为实践平台，运用模糊数学构建了贵州省高校体育教师的胜任力评价指标体系，以便为贵州省高校体育教师目标考核、评优评模、继续学习、在职培训等，提供客观的评价标准。

1 贵州省高校体育教师胜任力模糊综合评价原理

模糊数学是以不确定性的事物为研究对象，对众多影响因素或现象作出全面的评估的一种评价方法。根据要求，给每一个评价指标赋予[0，1]的一个实数，进行汇总计算。[1]本研究拟选取能够代表体育教师的胜任力的七个指标，进行科学评价。在实际评价操作过程中，把贵州省高校体育教师胜任力评价指标可看成是一个子集，选取具有代表意义的几个重要指标作为集合进行研究。这里我们设贵州省高校体育教师胜任力的评价因素集合为：

U=(u1，u2，u3，…，un)

同样，设贵州省高校体育教师胜任力各指标评价等级集：

V=(v1，v2，v3，…，vm)

评价因素U和等级评价V存在模糊关系，即可构建模糊子集R

模糊矩阵中各元素取值在[0，1]之间，主要是评价指标u1，u2，u3，…，un的评价值。同样，各指标隶属度为ai，矩阵A，记为A=(a1，a2，a3，…an)，A为评判指标U的模糊子集，ai表示ui所得“权重”，各指标权重总和

R、A与贵州省高校体育教师胜任力发展存在模糊关系，B是V上的模糊子集，记为：

B=AR

根据矩阵运算法则

B=AR

采用最大最小合成法，将A矩阵中的各元素与R矩阵中某列各元素按顺序逐一两两对比取较小值，共得n个数，再从n个数中取最大值，可得Ci。依此类推，共得m个数，记为：

(C1，C2，C3，…，Cm)

计算结果≠1，需归一化处理，记为

(C1/∑Ci，C2/∑Ci，C3/∑Ci，…，Cm/∑Ci}

i=1，2，3，…，m

以上数列即是对贵州省高校体育教师胜任力的综合定量评价。

2 贵州省高校体育教师胜任力综合评价过程

(1)根据以上步骤和评价原理，现用模糊数学评价方法对贵州省高校体育教师胜任力水平进行评价。首轮通过问卷调查法、专家访谈法、文献资料法，获取评价贵州省高校体育教师胜任力评价指标；经整理、筛选、评估研究得出社会责任、职业道德、基础知识、专业知识、心理品质、工作行为、科研能力这七个方面与贵州省高校体育教师胜任力综合评价高低有着密切关系，见表1。故设评价因素集合为：

U=(u1，u2，u3，u4，u5，u6，u7)

将评语因素分为五级：非常优秀、较优秀、优秀、一般、差，则评语因素集合为：

V=(v1，v2，v3，v4，v5)

(2)采用调查量表对长期从事贵州省高校体育工作研究的领导、教师、管理人员、科研人员共计35人，针对××高校体育教师，杨××、潘××、郑××、于××胜任力进行问卷调查，每个“考官”根据个人经验、熟悉领域、研究专长、体育认识在评价表的相应位置划“√”，最终统计结果见表2。

表2中，各项统计数除总参评人数，即可得出单因素评价矩阵：

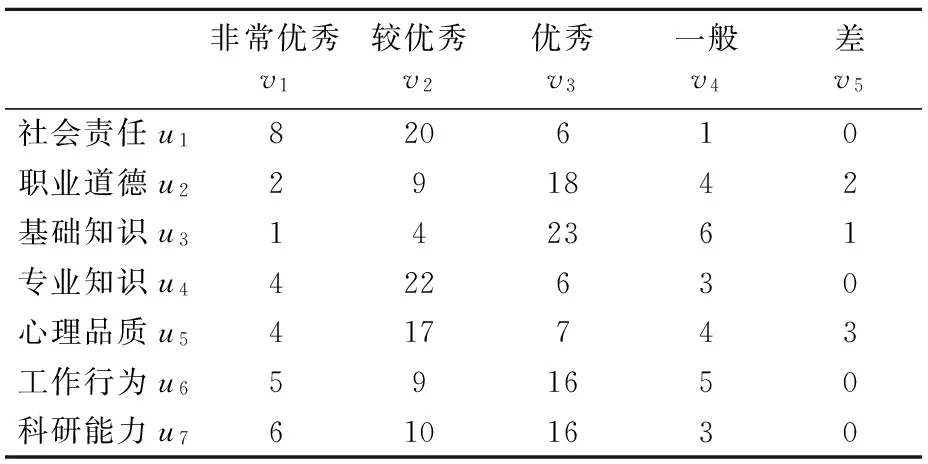
表2 贵州省高校体育教师胜任力综合评价(杨)一览表

(3)贵州省高校体育教师胜任力指标选取及权重分析，采用特尔斐法对指标进行筛选和建构，并向贵州九所高校，具有副教授职称及以上的体育教师发放15份调查问卷，收回15份。采用调查问卷方式对15位专家进行意见征询，经过三轮反复征询，从而得到贵州省高校体育教师胜任力评价指标。问卷设计按照重要(9)、较重要(7)、一般(5)、较不重要(3)、不重要(1)进行调查。各指标用M(平均数)表示专家的“意见集中度”；V(变异系数)表示专家“意见协调度”。V越小，专家的认同度越高。假设Xij表示第i个专家，第j个指标的打分，现在共有n个专家，m个指标。可表示为：

V:Vj=Sj/Mj

其中，Vj指j指标的变异系数，Sj指j指标标准差，Mj指j指标的算术平均数。Vj越小，j指标的专家意见协调度越高。由表3可知，贵州省高校体育教师胜任力七个指标的专家意见集中度，最小的职业道德平均值Mj>7.00，变异系数最大的基础知识为0.297 6。可以看出，专家的意见集中度、意见协调度均较高。说明这七个指标用来评价贵州省高校体育教师胜任力是可行的。

在构建的七个指标中，还需分配各指标的权重，运用层次分析法[4]确定各指标权重。每位专家对各指标采用1—9级进行了两两比较，经过方根法处理后，得出权重。大体分为三步：一，建立层次模型；二，构造判断矩阵；三，检验一致性。最后计算出平均值，各指标权重均通过一致性检验(CR<0.10)，计算过程略，各指标权重见表3。

最终贵州省高校体育教师胜任力评价指标对应的模糊子集为：

A=(0.11，0.13，0.15，0.20，0.14，0.18，0.09)

(4) 根据矩阵A与矩阵R建立模糊方程，得出体育教师杨××胜任力评价矩阵的合成，即

=(0.143，0.200，0.180，0.150，0.086)=0.759

计算结果和≠1，经归一化处理得出对体育教师杨××胜任力评价的最后结果：

(0.143/0.759，0.200/0.759，0.180/0.759，0.150/0.759，0.086/0.759)=(0.19，0.26，0.24，0.20，0.11)

表4 贵州省高校体育教师胜任力(杨××)综合评价百分比一览表

根据 “最大隶属原则”，体育教师杨××属于“较优秀”一类。将评语集中的诸元素(非常胜任、较胜任、胜任、勉强胜任、不能胜任)分别赋予对应的值，则可把综合评价换算成百分制。非常胜任(100～90 )、较胜任(90～80)、胜任( 80～70)、勉强胜任(70～60)、不能胜任(60以下)。由于各等级是区间值，取组中值即非常胜任95、较胜任85、胜任75、勉强胜任65、不能胜任55。

= 0.19×95+0.26×85+0.24×75+0.20

则评价综合最终得分77.16分。

同理计算出，体育教师潘××综合得分为74.14分、郑××72.21分、于××66.12分，综合得分大小依次为：杨××>潘××>郑××>于××。笔者构建的胜任力模型评价得分与几位教师年终目标绩效得分排序一致。说明运用模糊数学评价法对贵州省高校体育教师胜任力进行模糊综合评价具有可行性。

3 结论

运用社会责任、职业道德、基础知识、专业知识、心理品质、工作行为、科研能力七个指标，对贵州省高校体育教师胜任力进行模糊综合评价，结果与实际符合。利用模糊综合评价方法评定，方法简单，能客观、科学、定量评价，对于原来关系模糊、优劣界限不分明的评价指标体系，运用模糊数学进行评价，具有明显的优越性和操作性。

模糊数学综合评价方法从定性分析转化为定量分析，为评价工作提供了一种可量化的处理方法。

该评价方法的指标体系是根据访谈、调研得出来的，各指标的选择和权重分配是经过多位从事贵州省高校体育教师管理研究的相关人员，具有高度代表性。然而，每个调查人员的研究兴趣、研究领域和自身研究能力存在差异性，难免会存在各抒己见。

[1] 中华人民共和国中央人民政府.学校体育工作条例[EB/OL].http://www.gov.cn/fwxx/content_2267007.htm.

[2] 法规库.教育部关于印发《全国普通高等学校体育课程教学指导纲要》的通知[EB/OL]. http://china.findlaw.cn/fagui/p_3/97520.html.

[3] 梁保松，曹殿立.模糊数学及其应用[M].北京：科学出版社，2007.

[4] 张炳江.层次分析法及其应用案例[M].北京：电子工业出版社，2014.

[5] 夏崇德.综合评判在女排运动员选材中的运用[M].北京体育大学学报，2003，26(1):69～72.

[6] 沈钧毅.运用模糊数学对体育教学训练水平进行综合评价的研究[J].中国体育科技，2000，30(11)：13～15.

[7] 汪君民.义务教育阶段学生体育权利评价指标体系的构建及福建省实证研究[D].福州：福建师范大学，2011.