基于加Hamming窗FFT和db24小波包变换的电力系统谐波分析

李正国，全 菲

（1.深圳职业技术学院，广东 深圳 518055；2.南华大学 电气工程学院，湖南 衡阳 421005）

傅里叶变换（FFT）算法是目前电网中谐波分析常采用的方法，然而傅里叶变换是一种传统的谐波检测分析算法，虽然它能够精确地确定平稳信号中各次谐波的幅值等电力参数，但傅立叶变换对局部信号做处理相当于将信号作了平均，局部特征丢失了，无法判断奇异点的空间分布情况，即无法定位暂态信号发生的时间［1］。因此，FFT只适用于确定性的平稳信号谐波的分析，即使改进后的加窗傅里叶变换也仍然没有从根本上解决这一矛盾。

小波变换具有灵活时频特性，可以准确确定信号发生突变的时刻，滤除干扰信号，有效地从信号中提取信息。小波包变换将频带进行多次划分，对多分辨率分析没有细分的高频部分进一步分解，并能够根据被分析信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，从而提高了时频分辨率，因此，小波包具有更广泛的应用价值［2］。文献［3］利用加窗傅里叶变换有效抑制频谱泄露的特性提出了加窗傅里叶变换求稳态信号的频谱，文献［4-5］分别提出了基于FFT和小波包变换的电力系统谐波检测方法。

笔者将加窗傅里叶变换抑制频谱泄露和小波包变换准确确定信号发生突变的时刻及对频带进行多次划分具有较高分辨率的优点结合起来对电力系统谐波进行分析。该分析方法不仅可减少分析过程中的频谱泄露，得到比较准确的稳态谐波幅值，而且也能进行暂态信号发生和终止的时间及幅值分析。经过仿真实验结果证实，该方法在电力系统谐波分析中具有可行性，可为电力系统谐波的分析和治理提供依据。

1 基于加窗FFT和小波包变换的谐波检测法

1.1 频谱泄露

假设信号只含基波频率，则

矩形窗函数为

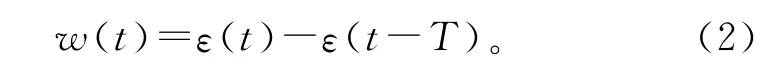
信号的傅里叶变换为

矩形窗函数的傅里叶变换为

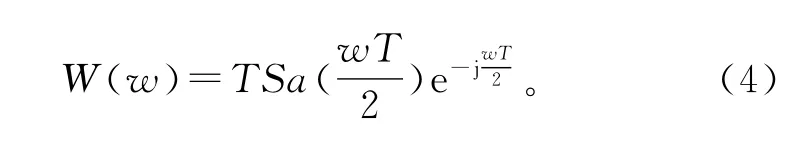
则离散化的输入信号傅里叶变换为

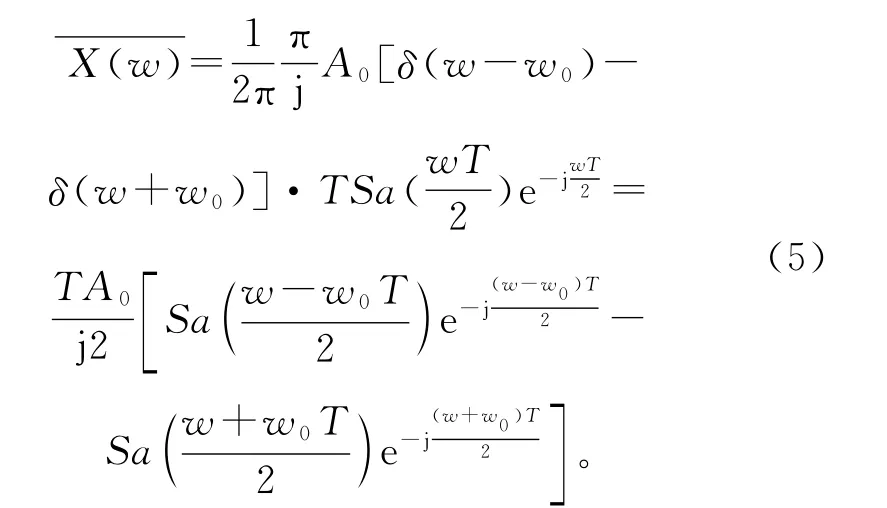
Sa（t）函数又称抽样函数，t≠0时，随着t的绝对值增大，函数值的绝对值震荡着不断减小，向0趋近。可以看出不是单一的谱线，而是扩散到整个频谱轴，即能量不再集中，发生了频谱泄露［6］。

1.2 加窗傅里叶变换

电网信号主要包含整数次谐波，基于余弦窗的窗函数特点：只要选择观测时间是信号周期的整数倍，则其频率在各次整数倍谐波频率处幅值为0，谐波之间不发生相互泄露。

窗函数的表达式为

可不是吗，没有味道了也就没有了兴趣，这似乎正暗示了两个人的爱情，刚好走到了尽头，刚好可以结束了。女人选择了缄默，换一个词来说可能是逃跑。

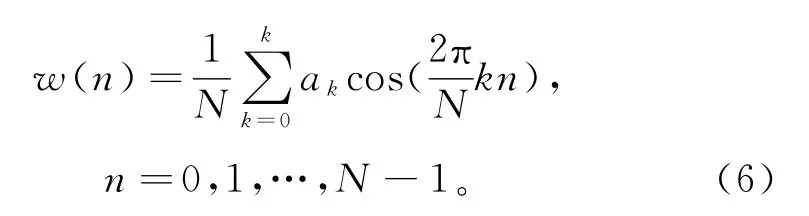
式中 ak决定了不同的窗，为了满足插值定理，则窗函数的离散傅里叶变换为

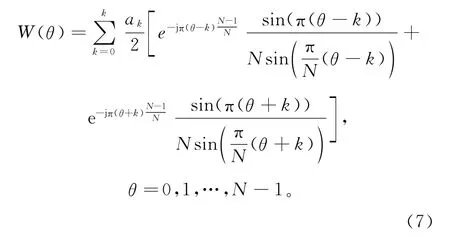
窗函数的选择原则：①主板尽量窄；②尽量减少窗谱旁瓣的相对幅度。该设计选用Hamming窗：

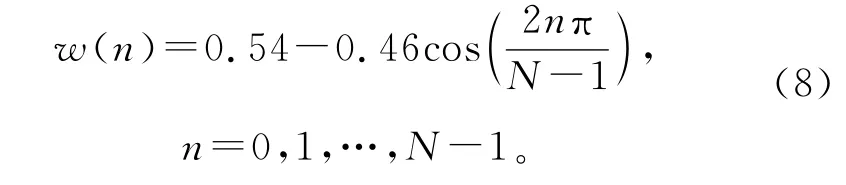
由加窗FFT变换求出其谐波含量及谐波主要分布范围，再由小波包变换求其细节。

2 小波包分析检测方法

信号的小波包分析过程：①对信号进行分解，得到基波和各次谐波分量在相应尺度空间上的系数；②根据基波和各次谐波分量在相应尺度空间上的系数，重构出基波信号和各次谐波信号，从而实现对谐波的检测。定义子空间是函数wn（t）的闭包空间，而是函数w2n（t）的闭包空间，并令wn满足双尺度方程：

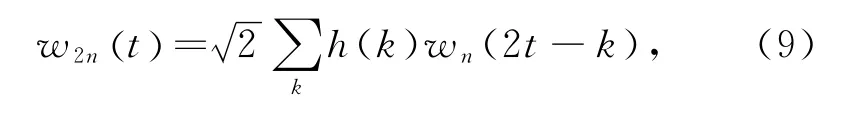
式中 k∈Z，g（k）=（-1）h（1-k）；

小波包重构算法为

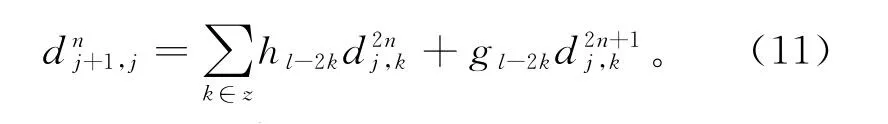
式中 hl-2k，gl-2k分别为小波包重构的低通和高通滤波器组总的分解层数。

目前，电网中存在的谐波以低次谐波（2～25次）为主，该设计需要分析31次以内的谐波。根据采样定理可知，fS≥2×50×31=3 100Hz，该设计中取fS=3 200Hz。对信号进行4层基于db24的小波包分析，在小波包分析的分解过程中，对0～fS／2的所有频段都进行高分辨率分析，加大谐波检测过程中的运算量，降低检测的实时性。

该设计选择db24小波包进行4层小波包分解。小波包算法将原始信号分解成一系列子带信号，用fS表示小波包分解各节点的频带，对0～1 600Hz频率的实际信号进行4层小波包分解后的16个频段的划分如图1所示［7］。

由图1看出，原始信号的4层小波包变换分解是一个完整的树型结构，对低频和高频部分均进行了分解，并且分解后每一个频带Un4都具有相同的带宽，也就是在每一个频带内所包含的谐波次数相同。小波包的空间分割可以把原始信号分解到不同的小波子空间，小波包的分解提高了对信号高频成分的分辨率。

图1 4层小波包分解Figure 1 Resolution of 4-layers wavelet packet

3 谐波检测方法的仿真实验

在该方法中，首先用加窗FFT变换检测出信号的各频率成分及稳态谐波的幅值。对于暂态的谐波信号，可以用小波包变换检测出其发生的时间和结束的时间，然后再利用加窗傅里叶变换对暂态信号发生的时间段进行分析得到暂态信号的幅值。同时，小波包变换对信号分析，可将检出信号中的衰减信号分离出来。

设电网中的信号在0～1s含有1，3，5，7次稳态谐波及21次谐波的衰减信号，即

在（1 500～2 000）／3 200时间段内出现11次谐波，其信号函数表示为

原始电网电压信号x（t）时域波形如图2所示。

图2 电网电压信号的时域波形Figure 2 Waveform of power grid voltage in time domain

3.1 加Hamming窗FFT运行结果显示

电网电压信号加窗傅里叶变换后幅频特性曲线如图3所示，可以看出，电网信号中含有50，150，250，350，550，1 050Hz的信号。

加Hamming窗FFT变换谐波幅值偏差如表1所示，从测试结果可以看出，该实验所采用的加Hamming窗傅里叶变换可以准确地求出1，3，5，7次谐波的幅值，而对含11次谐波的突变信号和含21次谐波的衰减信号的幅值测量结果误差非常大。说明加窗FFT只适合于稳态信号的谐波分析，而不适合用于分析暂态谐波。

图3 电网电压信号加窗傅里叶变换后幅频特性曲线Figure 3 Amplitude-frequency characteristic curve of power grid voltage after hamming window FFT

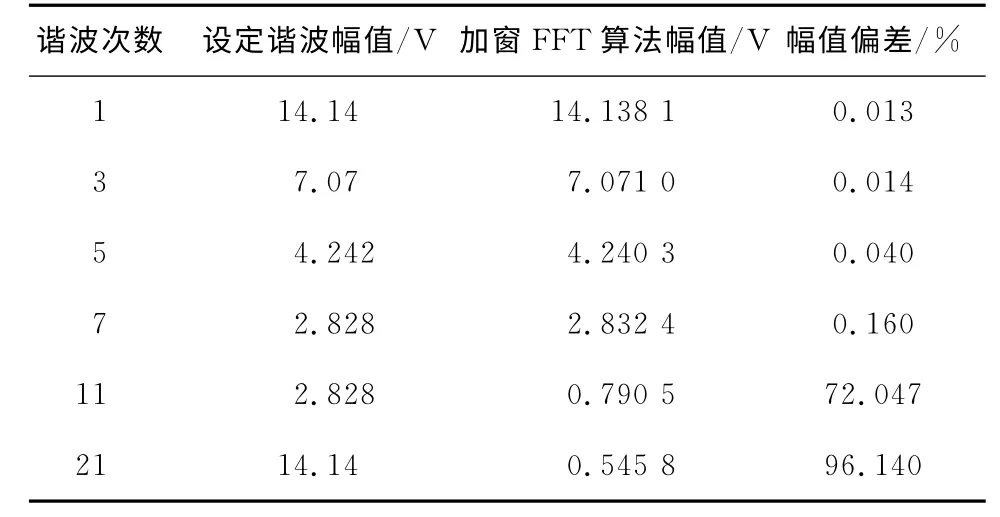
表1 加Hamming窗FFT变换谐波幅值偏差Table 1 Deviation of harmonic amplitude after hamming window FFT

3.2 基于db24的小波包分析

小波变换对衰减信号和突变信号有较好的检测与分析［8］，小波包［9］变换亦然，在进行小波包分解重构后可以得到比较准确的衰减信号和突变信号，采用4层小波包变换，仿真结果如图4～10所示。图4所示重构后的信号S130～S1315所对应的频段与图1第4层的频段相对应，可知S130对应的是0～100Hz的重构信号，该设计中对应为50Hz的基波频率。同理可知，S131，S132，S133，S137分别对应的是3，5，7，11次谐波重构信号，含21次谐波的衰减重构信号为S1315。由S135可以清晰地看到f=1 500和2 000Hz处出现了极大值点，说明含有11次谐波的暂态信号发生和终止时间分别为1 500／3 200≈0.469s和2 000／3 200=0.625s。从图5～9可以看出，小波包分解可以准确地重构基波信号，3，5，7，11次谐波重构有少许误差。从S1313中可以看出21次谐波衰减信号仍有少量泄露，但不影响分析。2 1次谐波衰减信号频率集中在1 050Hz处，可以直接重构第1层小波包分解的高频部分8 00～1 600Hz，得到更精确的衰减信号波形，图10即为对第1层小波包分解高频部分重构的波形。

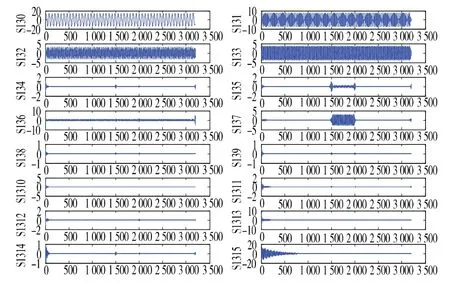
图4 db24小波包分解重构后的信号波形Figure 4 Waveform of signals after db24wavelet packet resolution and reconstruction

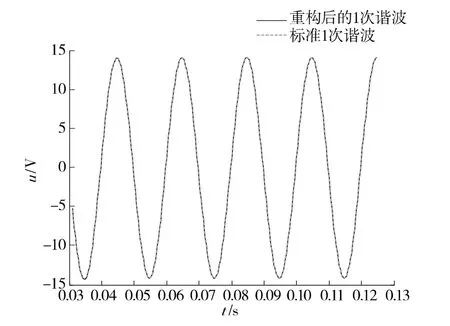
图5 重构的基波信号与标准基波信号对比Figure 5 Comparison of reconstructed fundamental wave and standard fundamental wave

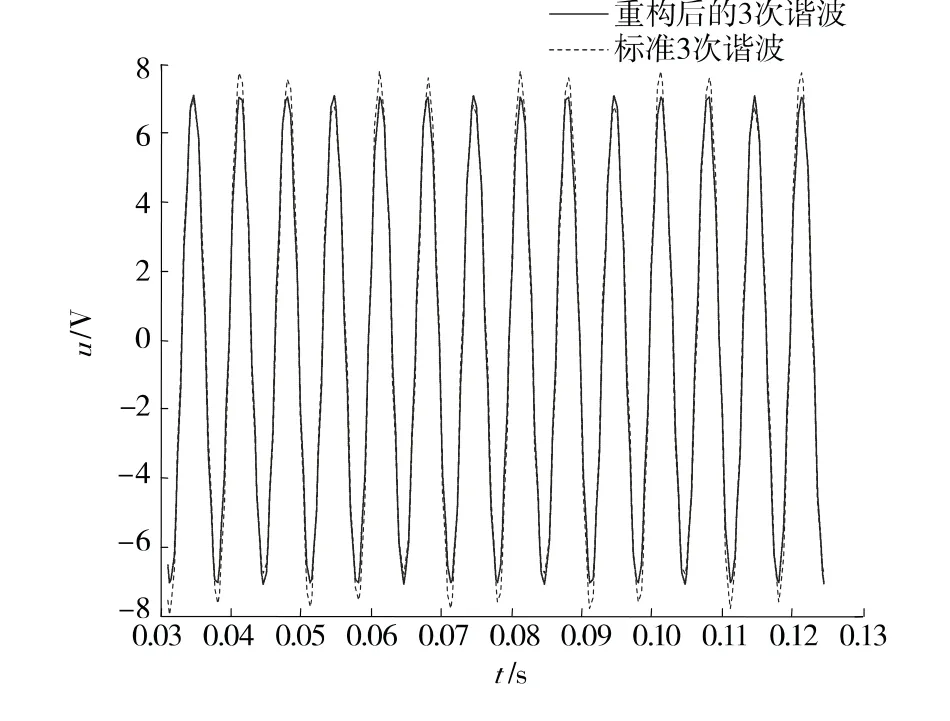
图6 重构后的3次谐波信号与标准谐波信号对比Figure 6 Comparison of reconstructed 3-harmonic wave and standard 3-harmonic wave

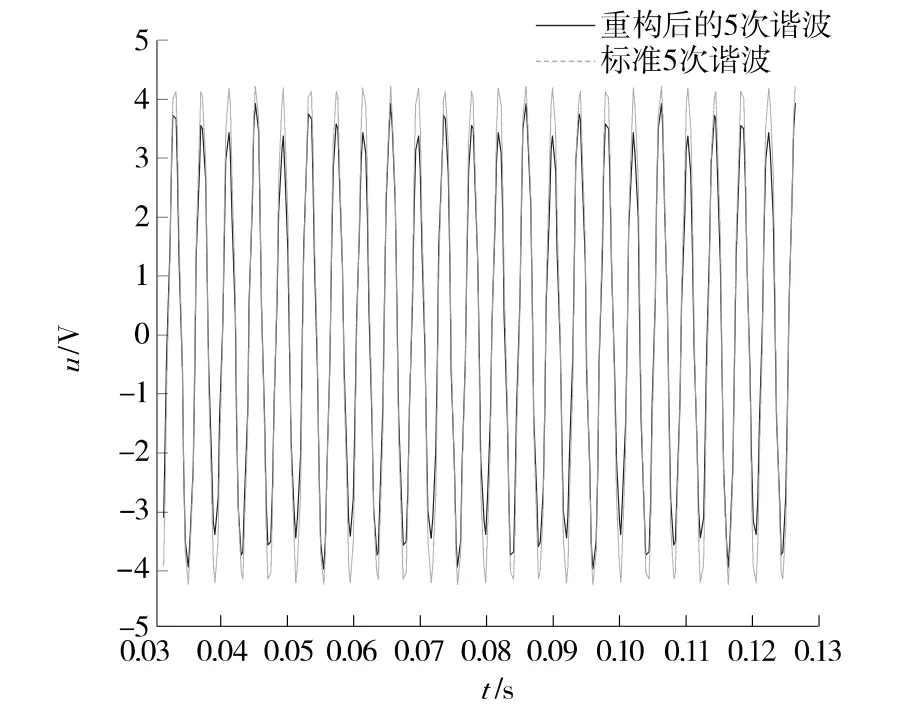
图7 重构的5次谐波信号与标准谐波信号对比Figure 7 Comparison of reconstructed 5-harmonic wave and standard 5-harmonic wave

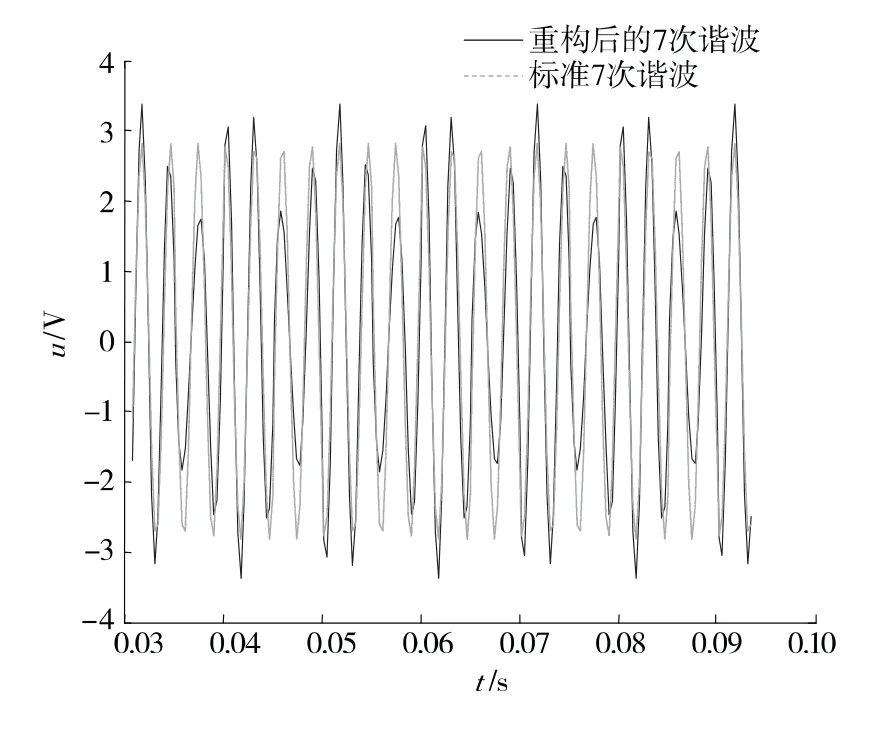
图8 重构后的7次谐波信号与标准谐波信号对比Figure 8 Comparison of reconstructed 7-harmonic wave and standard 7-harmonic wave

图9 重构后的11次谐波信号与标准谐波信号对比Figure 9 Comparison of reconstructed 11-harmonic wave and standard 11-harmonic wave

图10 重构后的衰减信号Figure 10 Attenuation signal after reconstruction

由小波包分解重构信号已经得到含11次谐波的暂态信号发生和终止的时间，则可以对（1 500～2 000）／3 200s时间段的信号进行加Hamming窗傅里叶变换，得到此段时间内11次谐波时的稳态谐波信号。通过仿真得到在（1 500～2 000）／3 200s内11次谐波的幅值为2.828 8，与设定的2.828之间的误差仅为0.028%。

4 结语

小波包分析具有许多优良的特性从而得到广泛应用。笔者给出分析电网谐波简单且有效的方法，通过MATLAB的仿真结果可以看出该方法不仅简单有效地提取了电网中存在的基波和各次稳态谐波，同时提取出了暂态信号，准确地定位暂态谐波发生的起始及终止位置，并且能够得到准确的谐波信号幅值。

［1］Sanoso S，Grady W M，Powers E J，et al.Characterization of distribute power quality events with Fourier and wavelet transforms［J］.IEEE Transations on Power Delivery，2000，15（1）：247-254.

［2］张德丰.MATLAB小波分析［M］.北京：机械工业出版社，2011.

［3］黄纯，江亚群.谐波分析的加窗插值改进算法［J］.中国电机工程学报，2005，25（15）：26-39.HUANG Chun，JIANG Ya-qun.Improved window and interpolation algorithm for analysis of power system harmonics［J］.Proceedings of the CSEE，2005，25（15）：26-39.

［4］薛蕙，罗红.小波变换与傅里叶变换相结合的暂态谐波分析方法［J］.中国农业大学学报，2007，12（6）：89-92.XUE Hui，LUO Hong.Transient harmonic analysis algorithm using wavelet transform and Fourier transform［J］.Journal of China Agricultural University，2007，12（6）：89-92.

［5］房国志，杨超，赵洪.基于FFT和小波包变换的电力系统谐波检测方法［J］.电力系统保护与控制，2012，40（5）：75-79.FANG Guo-zhi，YANG Chao，ZHAO Hong.Detection of harmonic in power system based on FFT and wavelet packet［J］.Power System Protection and Control，2012，40（5）：75-79.

［6］梁小民.加窗傅里叶变换谐波检测算法及其插值改进研究［J］.电力科学与技术学报，2007，22（3）：36-39.LIANG Xiao-min.Study on windowed fourier transform algorithm and its improvement with interpolated method for harmonic detection［J］.Journal of Electric Power Science and Technology，2007，22（3）：36-39.

［7］纪跃波.小波包的频率顺序［J］.振动与冲击，2005，24（3）：96-99.JI Yue-bo.Frequency order of wavelet packet［J］.Journal of Vibration and Shock，2005，24（3）：96-99.

［8］田立军，石国萍，孙英明.一种基于小波变换的电压波动和闪变的检测方法［J］.山东大学学报：工学版，2005，35（4）：39-42.TIAN Li-jun，SHI Guo-ping，SUN Ying-ming.The measurement method of voltage fluctuation and flicker using wavelet transform［J］.Journal of Shandong University：Engineering Science，2005，35（4）：39-42.

［9］沈申生，杨奕，高明.奇异性信号的检测［J］.低压电器，2005（5）：55-57.SHEN Shen-sheng，YANG Yi，GAO Ming.Detection of singularity signal［J］.Low Voltage Apparatus，2005（5）：55-57.