考虑热老化的油浸式变压器比例风险模型

郭创新，何 迪，张金江，鹿鸣明，杨秀瑜

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.深圳供电局，深圳 518001）

电力变压器是电力系统安全、可靠运行的关键枢纽设备，其健康水平直接影响着整个电力系统的安全运行。

一般情况下，变压器自身热积累及服役环境的共同作用导致了变压器故障［1］，其服役期间的故障率趋势可认为服从浴盆曲线［2］，投运初期故障率较高，之后故障率变化平稳，超过一定期限后随着服役年限的增加，故障率逐渐升高且趋势变急。故障率是变压器评判体系的重要指标［3］，对于及早发现变压器内部潜伏性故障、了解故障严重度、掌握故障的发展趋势意义重大［4］。

根据是否从历史数据进行数学统计分类，故障率模型可分为历史数据统计模型和非历史数据统计模型。相比于前者，后者充分考虑了变压器个体差异性，相对精确。根据适用的故障类型的不同，后者可分为①针对不可修复故障［5］的故障率模型，如老化失效［6］模型，是对变压器内部绝缘材料在变压器累积热效应作用下造成的不可逆损耗进行的建模；②针对可修复故障［5］的故障率模型，如以设备状态为输入的健康指数模型［7-8］，可以充分数据化变压器的在线监测信息、巡检信息以及相关状态试验结果［8］，同时响应变压器在实际运行过程由于维护操作导致健康度上升的过程［9］；③针对随机故障的故障率模型，模型输入一般为雷电等难以预估的气象因素，或者不可预见性人为事故引起的故障，现今较成熟的有天气相依的偶然失效模型［6］和两状态的天气模型［6］；④故障率综合模型，不可修复故障和可修复故障各有优势和侧重，但现有研究两者关系并进行综合建模的文献却很少。文献［10］虽然综合考虑了两者的互补作用，但仅将两类故障率计算结果进行简单加权，未考虑其间的复杂联系；文献［5］以Arrhenius定理［11］和变压器健康度为出发点，提出了以负载率和设备状态为输入的AWH模型，其建模方式较为复杂，实际中较难应用。

笔者以比例失效模型（Proportional Hazard Model，PHM）［12］为基础，得到以老化时间和油气信息为输入，响应变压器热老化和健康水平变化的综合故障率模型，即Arrhenius-HI-PHM，给出建模方法、具体步骤和模型参数估计方法，并采用实际监测的变压器故障进行算例分析，验证其有效性。

1 比例失效模型

在比例失效模型中，令变压器失效时间（设备从开始投运到首次发生故障而停止运行的时间）为T，故障概率分布函数为F（t），故障概率密度函数为f（t），可靠度函数为R（t），若设备在（0，t］都可靠运行，在（t，t+Δt］内发生故障的概率为

将式（1）两边同除以Δt，令Δt趋于0并取极限，得到故障率函数h（t）：

定义变压器的故障风险r为到检测时间t变压器正常工作，但在接下来的检测间隔期Δt内发生故障的概率，可以表示为

求解式（3），可得

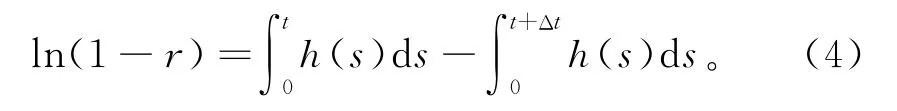
将式（2）变形，可得故障率函数为

式中 h0（t）表示以时间为自变量的基本故障率；Z为反映设备健康状态的协变量向量；γ表示协变量Z影响的协变量参数；exp（γZ）为协变量连接函数。

PHM认为状态变量对失效函数具有乘法效应，且γZ表示协变量的线性组合。该模型能有效地建立设备状态和设备故障率的联系，从而获得设备的可靠度［13］。

2 Arrhenius-HI-PHM建模步骤

2.1 基准故障率函数h0（t）的建模

h0（t）作为基准故障率函数可用来对应变压器老化失效。威布尔分布具有形状参数，可契合浴盆曲线变化趋势，已广泛应用于机械零部件的失效建模［13］。由于变压器失效情况与机械失效情况存在类比可能性，故笔者采用威布尔分布来表征变压器的基准故障率函数：

式中 β为形状参数；η为比例参数。该文考虑变压器中后期故障率建模，所以形状参数β＞1，此时故障率呈上升趋势。

式（6）中的t值为恒定θH下的等效t值。为了求出该值，可运用以变压器冷却系统类型为模型系数的“热点温度计算模型”［11］分析，得到热点温度曲线。之后将服役时间按热点温度值划分为n个小区间ti，每个小区间的热点温度θHi均保持恒定，累加可得等效时间［6］：

为了简化计算量，笔者估算出η值。变压器寿命可以用绝缘纸寿命Lt表示［11］，而绝缘纸的老化程度与绝缘系统中的热点温度服从Arrhenius定理，同时，热点温度可根据“热点温度计算模型［11］”计算获得：

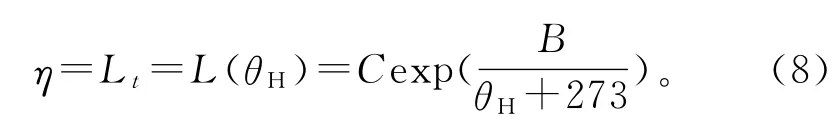
式中 B，C均为实验测得的经验常数；θH为绕组的热点温度。令基础热点温度θH=110℃，根据文献［11］可查阅得B，C参数的值，计算可得，η=7 500d（之后的计算时间都将以天为单位）。

2.2 协变量连接函数exp（γZ）的建模

exp（γZ）是协变量连接函数，对应于变压器健康水平，反映了不同状态Z（t）对设备故障率的影响：

Z（t）是一系列健康度指标的集合，既有设备内部变量，例如设备本体、套管等检测信息反应的可修复故障信息，还包括影响设备运行的外部变量，例如环境条件、气象条件等。因此，协变量条件个数为p时，连接函数exp（γZ）可以表示为

目前，电力部门普遍应用的其中一种能体现变压器在线监测信息，对健康水平的反映较为全面、客观的方法是变压器油中溶解气体分析（DGA）［14］。检测 的 气 体 一 般 有H2，CO，CH4，C2H4，C2H2，C2H6及其总量，也称为可燃性溶解气体总量（TDGC），另外还监测了总烃的相对产气速率和绝对产气速率等。在变压器的长期运行中，其内部的绝缘材料在物理化学作用下会逐渐老化分解，产生部分低分子烃类和CO等气体。正常情况下，这类气体的产生分解速度十分缓慢，但是在变压器内部有潜伏性故障条件下，其产生的速度和浓度都会增加。该文模型中的协变量采用的就是根据油气信息评估得到的健康状态。

评价变压器健康水平的方式有多种，其中一种是依据油气信息分级标准［15］进行状态分级，如表1所示。

表1 IEEE C57.104中依据DGA信息的状态划分Table 1 Dissolved gas concentrations for condition classification based on IEEE C57.104

当变压器分别处于正常、注意、异常、严重时，可认为连接函数中Z（t）=1，2，3，4，同时根据文献［16］对绝对产气速率的规定对变压器健康状态进行界定。理论上，变压器的故障率是连续的，虽然允许跳变，但跳变通常发生在内部故障或外部环境突变的情况下［9］，且与模型有关。若采用现有健康状态评估体系，变压器状态在未发生内外部突变的情况下仍会跳变，如在某时间点前后，变压器最严重状态量TDGC值分别为1 920和1 921，这一微小变化导致了变压器状态由2（注意）跳变成3（异常），从而导致故障率跳变，这对模型的精度影响很大。

为了解决该问题，笔者提出变压器劣化分级健康状态这种协变量建模新方式对协变量进行改进，使之既能表示变压器的状态分级，又能以一个连续量表征变压器状态。

在该方式下，x1，x2，…，xn分别表示变压器不同的油气信息状态量，如x1表示H2的量（μL／L）；λ1，λ2，…，λn表示不同油气信息对应的劣化分级健康状态，如λ1表示H2的劣化分级健康状态；an，bn，cn表示第n个油气信息状态量xn对应表1的临界值数据，如a1为100，b1为700，c1为1 800。则状态量xn的劣化分级健康状态λn为

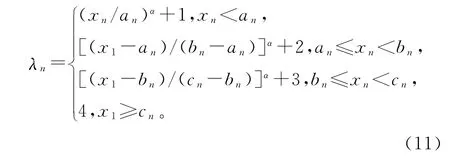
式中 α为参数变化对设备状态的影响因子［16］。该模型为了保证λn的连续性，α取1。该健康状态定义方式解决了不同数量级和量纲的状态量的状态等级匹配问题［17］。假设λ1，λ2，…，λn的最大值为λmax，则总体劣化分级健康状态可表示为

式中 ω表示次严重油气信息状态量的影响因子，一般由历史经验决定，根据文献［18］中对油中溶解气体的状态扣分规则是按标准最高扣分仅扣分一次，因此该模型ω取0。

按此方式算得的总体劣化分级健康状态的整数位表示分级所属类（正常、注意、异常、严重），以便工作人员直观了解变压器工作状态；小数位保证了计算故障率时的输入连续性。

由于油气信息的检测是间隔的，因此，在以劣化分级健康状态得出变压器状态后，该模型假定当ti≤t＜ti+1时，Z（t）=Z（ti），即该监测点和下一监测点间变压器状态不变［19］。

2.3 参数估计方法

笔者采用极大似然法进行模型参数估计。由故障概率密度函数f（t）可推导出可靠度函数R（t）。当协变量的函数形式已知时，需要参数估计的参数有β，η，γ，则一般形式的似然函数为［20］其中，样本总体个数为n；是否截尾的状态量为δi，截尾数据用0表示，失效数据用1表示；观测到的寿命时间的样本集为Q，其中失效个数为q。截尾数据表示换油前的监测终点，失效数据表示变压器故障时的数据。

协变量与时间相关，因此相应似然函数为

取对数得

其中，样本总体个数为n，失效个数为q，ti表示第i个失效个体在基准温度θH对应的等效时间，协变量条件的个数为p，s为变压器个体在θH下的等效检测时间点。

如要记录每台变压器长时间跨度的油气信息，其数据量十分庞大，同时在数据保存过程中难免发生数据丢失情况，这为参数拟合带来了难度。为了解决数据缺失问题，该模型降低了对未失效变压器油气信息的要求，使在油气信息不全的情况下也能通过简化模型拟合参数。若未失效个体中有详细油气信息记录的个体个数为m，其余个体油气信息缺失时，假设其余个体油气信息变化过程与有详细油气信息个体类似，可将式（15）变形，得

将各参数求一阶导数并置于零，由于η已知，可得到一组关于β，γ的超越方程组，此后可采用合适算法求 解 得 到

3 算例分析与软件实现

3.1 参数拟合

已知监测的11台相同变压器中的1台发生了故障，且记录了该失效变压器的失效时间和失效时的油气信息，如表2如示，以及4组长时间跨度的正常运行变压器T1—T4的油气信息（由于数据众多，只列出T1的油气数据，如表3所示），取式（16）中m=4，算例中的时间均为等效时间，通过模型计算可得变压器故障率，进而预测故障。

根据改进后的协变量可以得到变压器的劣化分级健康状态和总体劣化分级健康状态，如ω取0、失效变压器处于失效状态时，H2的劣化分级健康状态为1.887，总体劣化分级健康状态为3.411。因此，可作出变压器T1—T4的总体劣化分级健康状态变化图，如图1所示。

图1 T1—T4变压器劣化分级健康状态散点图Figure 1 Deterioration classifiable health status scatter-plot of the T1—T4transformers

根据模型，拟合得β=4.384 1，γ=0.760 4，延长时间跨度，将换油后的信息同时反映在故障率曲线上，可得变压器T1换油前、后的故障率曲线，如图2中“m=4”曲线，可见故障率相较于换油前有所降低，且故障增长趋势有所减缓。在这种建模方式下，1 800d时的日故障率换算得的年故障率约为0.018，这与文献［21］中统计得到的服役期为6年的变压器故障率基本吻合。

极端条件下，当未失效变压器中只有一组变压器有详细油气信息纪录时（如只有T1数据有详细纪录），模型参数仍是可估计的，此时取式（16）中m=1，拟合得β=3.925 9，γ=0.571 3，故障率曲线如图2中“m=1”曲线。该拟合参数下的故障率曲线与m=4时相比，已一定程度上反映出了变压器故障的发展趋势，但由于数据的简化，使得模型的精度有所降低，此时的参数基本已不具备代表性。为保证模型的精度，应尽可能保证数据输入的完整度，力求m接近于n甚至m=n。

图2 换油前、后变压器T1故障率散点图Figure 2 Failure rate scatterplot of the T1transformer before and after the oil change

3.2 检测间隔期的计算

根据式（4）可推断变压器的检测间隔期为

当变压器故障风险r已定，由式（17）可算得变压器所有时段的检测间隔期。如，假定变压器处于失效数据但未失效时，规定故障风险r为0.1%，根据模型计算得到检测间隔期为10.441 1d，这表明，若要求该次检测后变压器发生故障的概率低于0.1%，下一次的检测时间距这次的检测时间不应超过10.441 1d。在该故障率模型下，每个时间状态点都对应一个检测间隔期，这有助于电力部门合理安排检修计划。

表2 失效变压器失效时状态数据Table 2 Failure status data of the failure transform

表3 变压器正常运行时状态数据Table 3 Status data of the transform during the normal operation

4 结语

通过分析得出，笔者搭建的这种考虑温升老化和设备健康状态的油浸式变压器比例失效模型具有优点：

1）模型综合考虑了不可修复故障中的热老化和可修复故障中油气健康水平对变压器故障率的影响，既能响应变压器在累积热效应作用下的不可逆损耗，又能响应由于设备健康水平下降造成的故障和维护操作导致的健康水平上升过程；

2）劣化分级健康状态的协变量建模方式，充分契合故障率变化规律，在模型机制上减少了故障率无端跳变的可能，是一种全新的建模思路；

3）模型参数的拟合对数据量依赖性不强，即使油气信息不完整，只要失效变压器失效时刻的油气信息和其中几组正常变压器的油气信息，仍可估算出模型参数。这降低了模型的输入要求，使模型能得到更多应用。

［1］彭宁云.基于DGA技术的变压器故障智能诊断系统研究［D］.武汉：武汉大学，2004

［2］张黎，张波.电气设备故障率参数的一种最优估计算法［J］.继电器，2005，33（17）：31-34.ZHANG Li，ZHANG Bo.An algorithm for optimal parameter estimation of the failure rate of electrical equipment［J］.Relay，2005，33（17）：31-34.

［3］马仲能，钟立华，卢锴，等.基于电力设备全寿命周期成本最优的检修策略研究［J］.电力系统保护与控制，2011，39（16）：34-39.MA Zhong-neng，ZHONG Li-hua，LU Kai，et al.Study on the maintenance strategy of power equipment based onthe optimal life cycle cost［J］.Power System Protection and Control，2011，39（16）：34-39.

［4］郭创新，王越，王媚，等.表征内部潜伏性故障的变压器时变停运模型研究［J］.中国电机工程学报，2013，33（1）：63-69.GUO Chuang-xin，WANG Yue，WANG Mei，et al.Time-varying outage model for transformers representing internal latent fault［J］.Proceedings of the CSEE，2013，33（1）：63-69.

［5］张翔，宋子彤，杨致慧，等.一种基于负载率和设备检测信息的油浸式变压器故障率模型［J］.电网技术，2013，37（4）：1 159-1 165.ZHANG Xiang，SONG Zi-tong，YANG Zhi-hui，et al.A failure model for oil-immersed transformer based on load factor and equipment inspection information［J］.Power System Technology，2013，37（4）：1 159-1 165.

［6］何剑，程林，孙元章，等.条件相依的输变电设备短期可靠性模型［J］.中国电机工程学报，2009，29（7）：39-46.HE Jian，CHENG Lin，SUN Yuan-zhang，et al.Condition dependent short-term reliability models of transmission equipment［J］.Proceedings of the CSEE，2009，29（7）：39-46.

［7］Hughes D.Condition based risk management（CBRM）-enabling asset condition information to be central to corporate decision making［C］.18th International Conference and Exhibition on Electricity Distribution，Turin，Italy，2005.

［8］王慧芳，杨荷娟，何奔腾，等.输变电设备状态故障率模型改进分析［J］.电力系统自动化，2011，35（16）：27-31，43.WANG Hui-fang，YANG He-juan，HE Ben-teng，et al.Improvement of state failure rate model for power transmission and transforming equipmen［J］.Automation of Electric Power Systems，2011，35（16）：27-31，43.

［9］宁辽逸，吴文传，张伯明.运行风险评估中的变压器时变停运模型（一），基于运行工况的变压器内部潜伏性故障的故障率估计方法［J］.电力系统自动化，2010，34（15）：9-13.NING Liao-yi，WU Wen-chuan，ZHANG Bo-ming.Timevarying transformer outage model for operational risk assessment part one condition based failure rate estimation method for transformer internal latent fault estimation［J］.Automation of Electric Power Systems，2010，34（15）：9-13.

［10］Anders G，Otal S，Hjartarson T.Deriving asset probabilities of failure：effect of condition and maintenance levels［C］.Power Engineering Society General Meeting，Montreal，Quebec，Canada，2006.

［11］IEEE Std C57.91—1995.IEEE guide for loading mineral-oil-immersed transformers［S］.

［12］Cox D R.Regression models and life-tables［J］.Journal of the Royal Statistical Society，Series B（Methodological），1972：187-220.

［13］丁锋，何正嘉，訾艳阳，等.基于设备状态振动特征的比例故障率模型可靠性评估［J］.机械工程学报，2009，45（12）：89-94.DING Feng，HE Zheng-jia，ZI Yan-yang，et al.Reliability assessment based on equipment condition vibration feature using proportional hazards model［J］.Journal of Mechanical Engineering，2009，45（12）：89-94.

［14］Kelly J J.Transformer fault diagnosis by dissolved-gas analysis［J］.IEEE Transactions on Industry Applications，1980（6）：777-782.

［15］IEEE Std C57.104—2008.IEEE guide for the interpretation of gases generated in oil-immersed transformers［S］.

［16］顾煜炯，董玉亮，杨昆.基于模糊评判和RCM分析的发电设备状态综合评价［J］.中国电机工程学报，2004，24（6）：189-194.GU Yu-jiong，DONG Yu-liang，YANG Kun.Synthetic evaluation on conditions of equipment in power plant based on fuzzy judgment and RCM analysis［J］.Proceedings of the CSEE，2004，24（6）：189-194.

［17］骆思佳，廖瑞金，王有元，等.带变权的电力变压器状态模糊综合评判［J］.高电压技术，2007，33（8）：106-110.LUO Si-jia，LIAO Rui-jin，WANG You-yuan，et al.Fuzzy synthetic evalution of power transformer condition with variable weights［J］.High Voltage Engineering，2007，33（8）：106-110.

［18］Q／GDW 170—2008.油浸式变压器（电抗器）状态评价导则［S］.

［19］Banjevic D，Jardine A K S，Makis V，et al.A controllimit policy and software for condition-based maintenance optimization［J］.Infor，2001，39（1）：32-50.

［20］Kalbfleisch J D，Prentice R L.The statistical analysis of failure time data［M］.New york：John Wiley ＆Sons，2011.

［21］孙鹏，陈绍辉，张彩庆.基于Marquardt法参数估计的变电设备寿命周期故障率评估［J］.电力系统保护与控制，2012，40（1）：85-90.SUN Peng，CHEN Shao-hui，ZHANG Cai-qing.Assessment of failure rate for substation equipment life cycle based on Marquardt parameter estimation method［J］.Power System Protection and Control，2012，40（1）：85-90.