重建点模型的EM迭代成像
孙守思,邱 钧,桂志国,刘 畅
(1.中北大学电子测试技术国家重点实验室,山西太原030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西太原030051;3.北京信息科技大学应用数学研究所,北京100101)
发射式断层成像[1]中,核素在被测物内发生衰变时释放出正电子,正电子极易与周围电子发生湮灭,发射出共线光子对.探测器通过捕获这样一对光子来侦测出湮灭事件的发生,并且捕获的光子对数就是湮灭事件累计发生的次数.断层内任意一点处发生湮灭事件是随机的,由于湮灭过程伴随着光子对的出射,因此任意一点发射出的光子对也是随机的.设断层内某点处在各个方向下的光子发射密度均为λ,该点向任意方向发射光子这一事件均以固定密度随机独立地出现,这一随机事件在单位时间内出现的次数近似满足泊松分布.
通过泊松概率模型来描述放射性物质发射粒子这一物理现象,能很好地刻画观测数据的统计特性,使之更为贴近实际情况.本文针对传统模型[2-3]在离散过程中存在误差这一缺点,引入重建点模型[4],讨论了新模型下加窗基函数[5]的应用.最后,给出了基于重建点模型的EM[6-8]迭代格式,并进行了实验验证.
1 传统离散化模型
在传统离散化模型中,待重建区域被剖分成若干矩形像素格,每个像素格内各点的发射密度均相同.对于像素格j,设光子在各个方向下的发射密度均为 λj.
在像素格j内,任意一点 (x,y)向各个方向发射的光子均以固定的平均密度 λj随机独立地出现,那么,这一随机事件在单位时间内发生的次数(该点在任意方向下发射出的光子数)Bj(x,y)则服从泊松分布
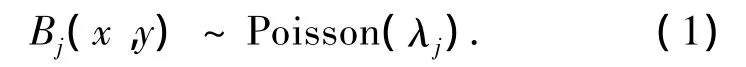
同样,在像素格j内每一点沿探测线i方向发射的光子都是一个随机事件,故在被探测线i穿过的这些点处,则发生了一系列的随机事件.这些随机事件在单位时间内发生的次数(像素格j发射出的光子被探测器接收到的数目)Bij同样满足泊松分布

对式(2)整理可得

式中:aij为探测线 i被像素格 j截取的长度.
由于传统的离散模型和中心旋转的扫描模式不匹配,导致了不同角度下到像素格中心点距离相等的射线与像素格的截格长度差别较大(如图1所示),这会对线积分的离散化近似带来误差.

图1 到中心点距离相等的射线Fig.1 Rays with equal distance from center
2 重建点模型
如图2所示,从待重建图像中抽出N个具有代表性的点,这些点均匀地排成横竖相等的阵列.每个点都是其周围一个理想小区域的中心点,即每个小区域可以由该点描述.在新的模型中,没有像素格的概念,每个重建点直接对应图像重建中要显示的像素.
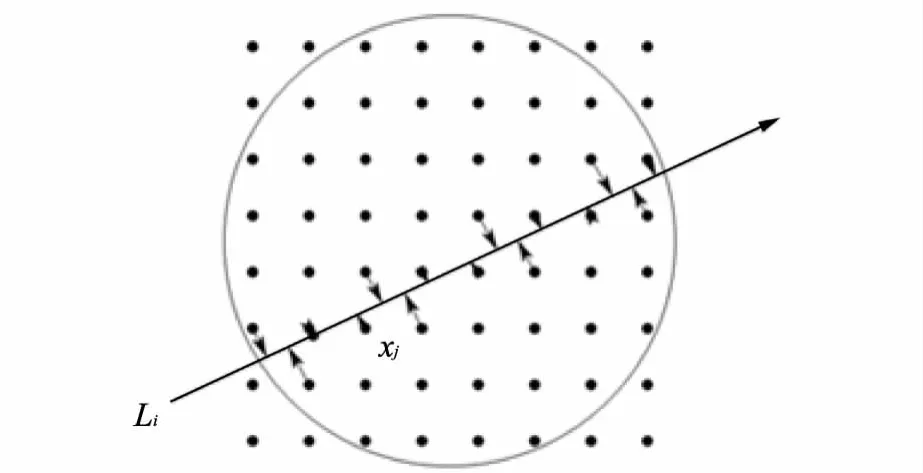
图2 重建点模型Fig.2 Reconstruction points model
在离散重建点模型中,假设理想区域内中心重建点发射密度已知,那么该区域内各点的发射密度均可由中心重建点插值求得.本文选用基函数法进行插值,进而得到连续的重建图像.
2.1 基函数法
图像的基函数可以理解为图像的基,任何图像均可由基函数线性组合而成.对任一图像f(x,y),设它对应的基函数为 b(x,y),则必存在实数λ1,λ2,…,λj,使得
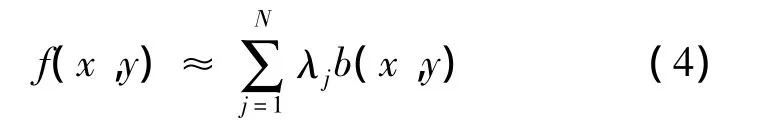
成立.这里的λ1,λ2,…,λj即是要求的光子发射密度.
在重建点离散化模型中,所选取的基函数b(x,y)要尽量满足局部完整,即在重建点理想区域内,基函数是完整或近似完整的,并且在理想区域边缘处保持连续平滑.基函数定义如下:
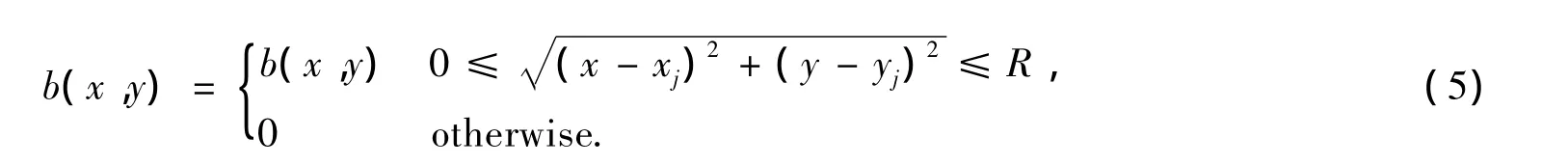
基函数在空域内的图形如图3所示.
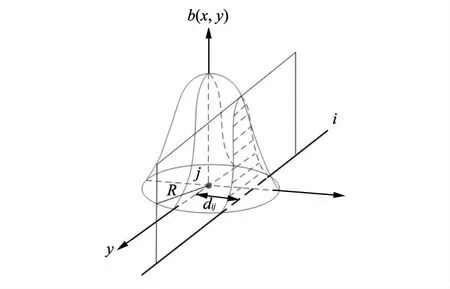
图3 基函数示意图Fig.3 Diagram of basis function
在图3中,基函数在理想区域内旋转对称,理想区域半径为R,中心重建点j到探测线i的垂直距离为dij,阴影部分为该理想区域的基函数被射线所在平面截得的截面.
在使用基函数来描述重建点理想区域时,通常需要对其进行截断.最简单的方法是加矩形窗,但会导致窗外的时域信息全部消失,从而引起频域频谱泄漏.在实际应用中,要选用合理的加窗函数,从而使频谱的扩散减到最少.
在选择窗函数时,应尽量满足主瓣较宽,旁瓣高度较低,同时还要结合基函数的特点来加窗,不仅能取得较好的效果,还便于计算.设加窗函数为 w(x,y),窗的长度为 2R,加窗后的基函数为

2.2 基函数实例
R.M.Lewitt[9]选取径向对称函数作为基函数,定义如下:
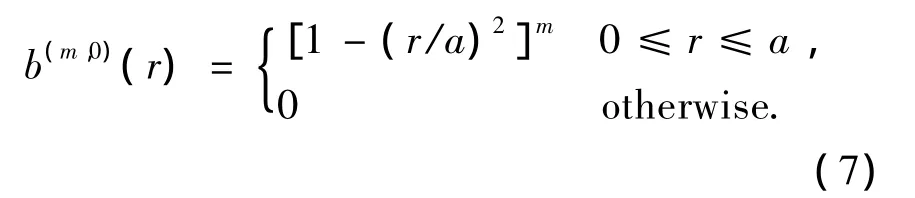

然后选取与基函数形似的Kaiser-Bessel窗函数
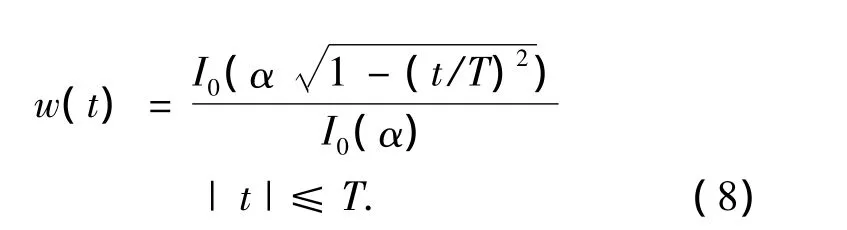
最后对基函数加窗,得到参数可调的广义基函数,定义如下:
在m=2,α=4和a=1的情形下,对基函数、Kaiser-Bessel窗函数和加窗基函数的切片做频谱分析,仿真结果如图4所示.
图4表明,加窗基函数旁瓣高度明显降低,频谱扩散也得到了抑制.通过对截断的基函数加窗,不仅使基函数在截断处变得平滑,在频域上也会尽量压低基函数旁瓣的高度,使能量集中在主瓣,高频分量减少,有效地抑制了基函数之间因旁瓣相互叠加而造成的频谱混叠现象.因此,加窗基函数方法在实际应用中切实可行.

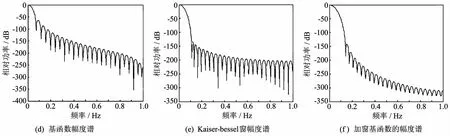
图4 加窗基函数频谱图Fig.4 Windowed basis function in frequency domain
3 重建点模型的EM迭代重构
在重建点离散化模型的理想区域内,任意一点(x,y)向各个方向发射光子均以固定的平均密度λjbw(x,y)随机独立出现,那么该事件在单位时间内发生的次数(该理想区域内某点在任意方向下发射出的光子数)Bj(x,y)则服从泊松分布,即
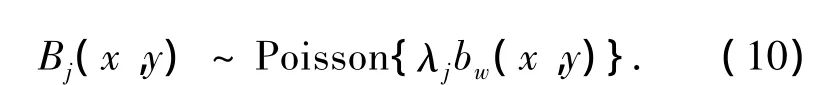
同样,在重建点j理想区域内,每一点沿探测线i方向发射光子都是一个随机事件,故在被探测线 i穿过的这些点处,则发生了一系列的随机事件.这些随机事件在单位时间内发生的次数(该理想区域发射出的光子被探测器 i接收到的数目)Bij同样满足泊松分布,即
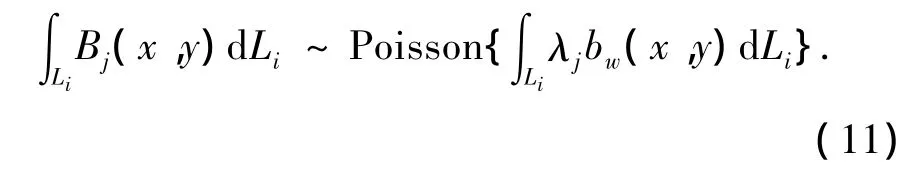
对式(11)整理得
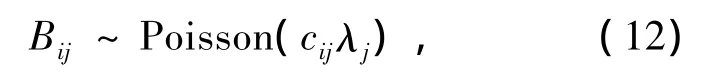
设随机变量bi为探测单元i上记录的光子数,则有

由于Bij~Poisson(cijλj)相互独立,因此有
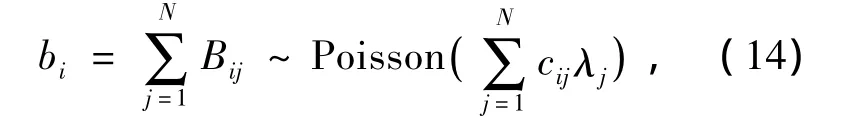
式中:bi是可观测到的光子数,它是由不可观测但却完整的 Bij组成的.
由于bi是独立的泊松变量,因此其联合概率密度函数为

对联合概率密度函数取对数可得
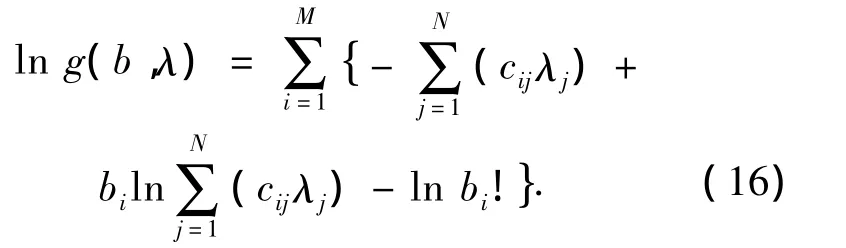
对ln g(b,λ)求关于参数λ的二阶偏导,可得
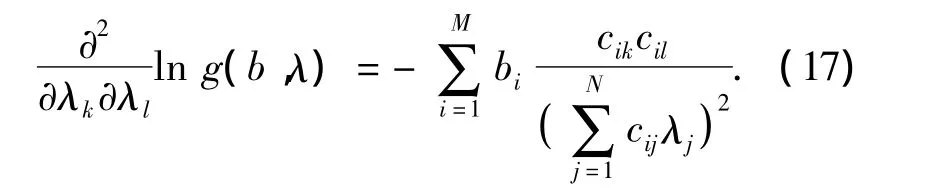
由式 (17)可知,lng(b,λ)呈严格凹性.
在经典EM算法中,需要考虑完备的投影数据,故对不可观测变量Bij求其联合概率密度
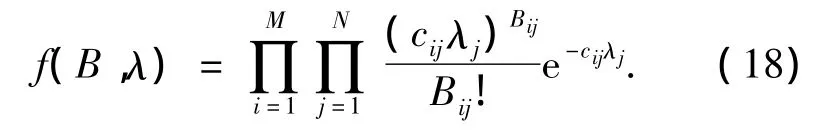
对式(18)取对数可得

EM算法:
1)E-step.对式(19)取在观斥数据 bi和当前估计参数λn下的条件期望.

其中:
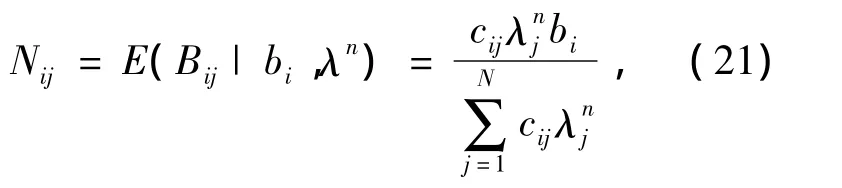
式中:R与参数λ无关,视为常量.
2)M-step.使条件期望最大化,对期望步求偏导得

令式(22)为零并进行整理,可得到EM迭代格式

4 数据实验
4.1 模拟数据的数值实验
本文采用一组模拟数据,选择传统模型下的经典EM算法和重建点模型下的EM算法重建图像.该模拟数据的角度采样数为576,平行线采样数为721.该实例中重建图像采用的分辨率为600×600,如图5~图7所示.

图5 鹦鹉原图Fig.5 Original image of parrot

图6 鹦鹉的投影数据位图Fig.6 Projection data bitmap of parrot

图7 经典EM迭代不同轮次的重建结果Fig.7 Results of classical EM algorithm under different numbers of iterations
本文采用下面两个图像距离的测量值来评价不同算法的重建图像质量.
1)归一化均方距离判断d
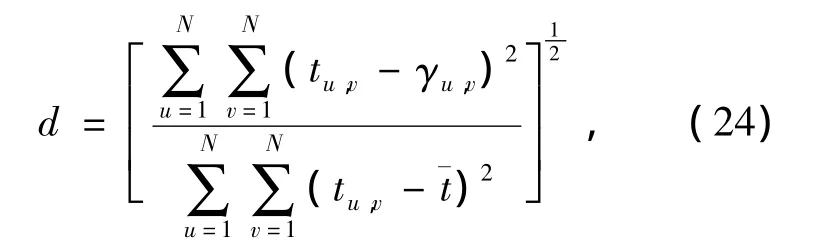
式中:tu,v和 γu,v分别表示测试模型和重建后图像中第 u行、第v列的像素密度;¯t为测试模型密度的平均值;图像的像素格个数为N×N个.d=0表示重建后图像真实地再现测试模型图像,d值愈大表示两者的偏差愈大.
2)归一化平均绝对值距离判断r
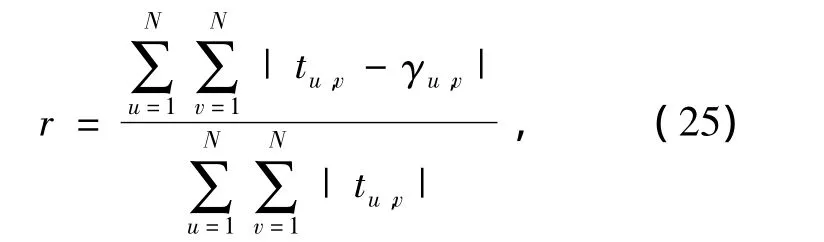
r=0说明没有误差,r增大说明误差增大.经典EM迭代一定次数后的误差如表1所示.

表1 经典EM迭代一定次数后的误差分析表Tab.1 Errors of classical EM under some number of i terations
这里选取m=1时对应的基函数,对不加窗基函数和加窗基函数分别进行了两组数据实验.①不加窗的基函数,选取α=0的情形.②加窗基函数,选取α=4的情形.重建点模型不加窗基函数EM的误差和重建结果如表2和图8所示.重建点模型加窗基函数EM的误差和重建结果如表3和图9所示.
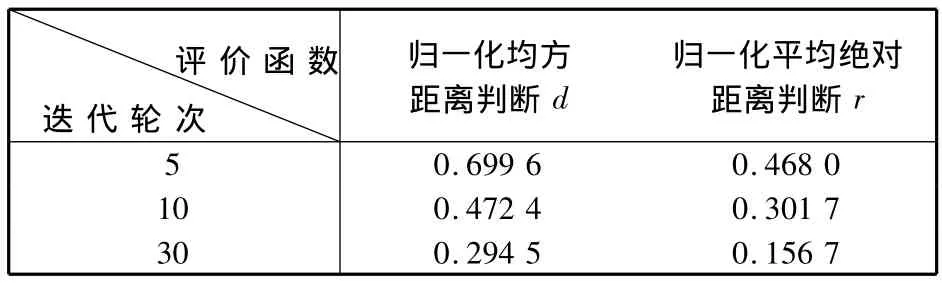
表2 重建点模型不加窗基函数EM的误差分析表Tab.2 Errors of EM with no window basis function under new discrete model

图8 重建点模型不加窗基函数EM的重建结果Fig.8 Results of EM with no window basis function under new discrete model

图9 重建点模型加窗基函数EM的重建结果Fig.9 Results of EM with windowed basis function under new discrete model

表3 重建点模型加窗基函数EM的误差分析表Tab.3 Errors of EM with windowed basis function under new discrete model
实验表明,在相同迭代次数时,传统模型下EM重建图像与原图误差较大,而重建点模型下EM重建图像的误差相对更小,重建后图像的质量也要好于前者.随着迭代次数的增加,重建图像与原图像的距离逐渐减小,图像越来越趋近于原图,重建效果越来越好.对比两组实验发现,加窗基函数EM重建出的图像误差要小于不加窗基函数EM的,这表明窗函数有减小误差的作用.
4.2 实测数据的数值实验
本节采用实测陶瓷叶片的数据,重建的图像需要强调细小裂纹特征.选取重建点EM算法重建图像,比较在不同迭代次数下图像的裂纹变化情况.该陶瓷叶片的实测数据量是576×241,该实例中采用的图像分辨率为256×256.实测投影数据位图如图10所示,经典EM迭代不同轮次的重建结果如图11所示.
同样,这里选取m=1时对应的基函数,并且分别对不加窗的基函数和加窗基函数进行两组数据实验.①不加窗的基函数,选取α=0的情形,如图12所示.②加窗基函数,选取α=4的情形,如图13所示.
由图12和图13的像素曲线图可以看出,随着迭代次数的增加,图像的灰阶变化越来越明显,细节越来越突出,与经典EM算法相比,曲线也较为平滑,这表明重建点模型下的EM算法能突出陶瓷叶片的细小裂纹特征,并且有抑制噪声的作用.

图10 实测投影数据位图Fig.10 Measured projection data bitmap
模拟数据和实测数据的数值实验表明,重建点模型较之传统模型减小了误差,EM算法对该模型的重构是有效的,可以在一定程度上提高成像的精度和质量.
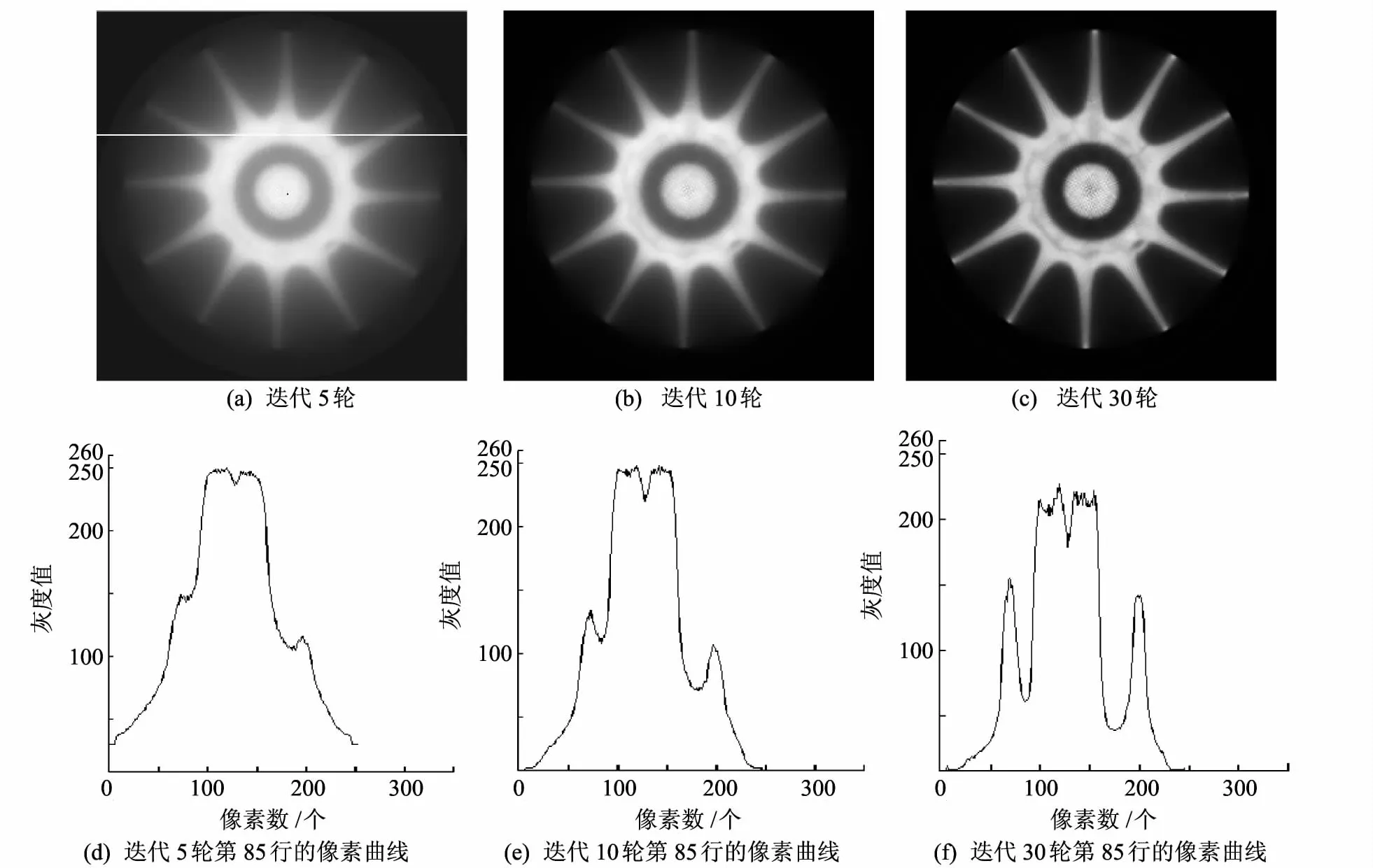
图11 经典EM迭代不同轮次的重建结果Fig.11 Results of classical EM algorithm under different numbers of iterations
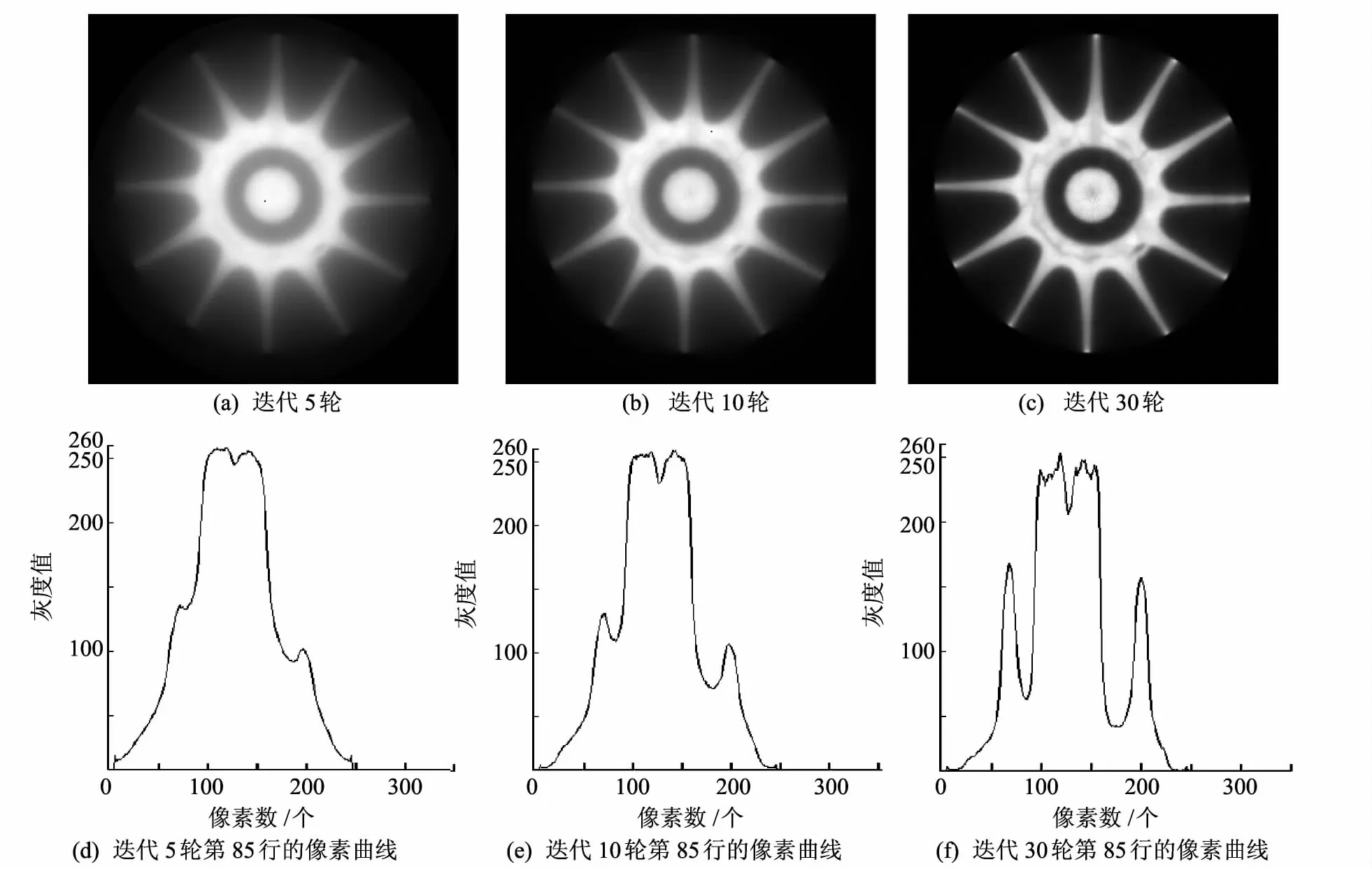
图12 重建点模型不加窗基函数EM的重建结果Fig.12 Results of EM with no window basis function under new discrete model
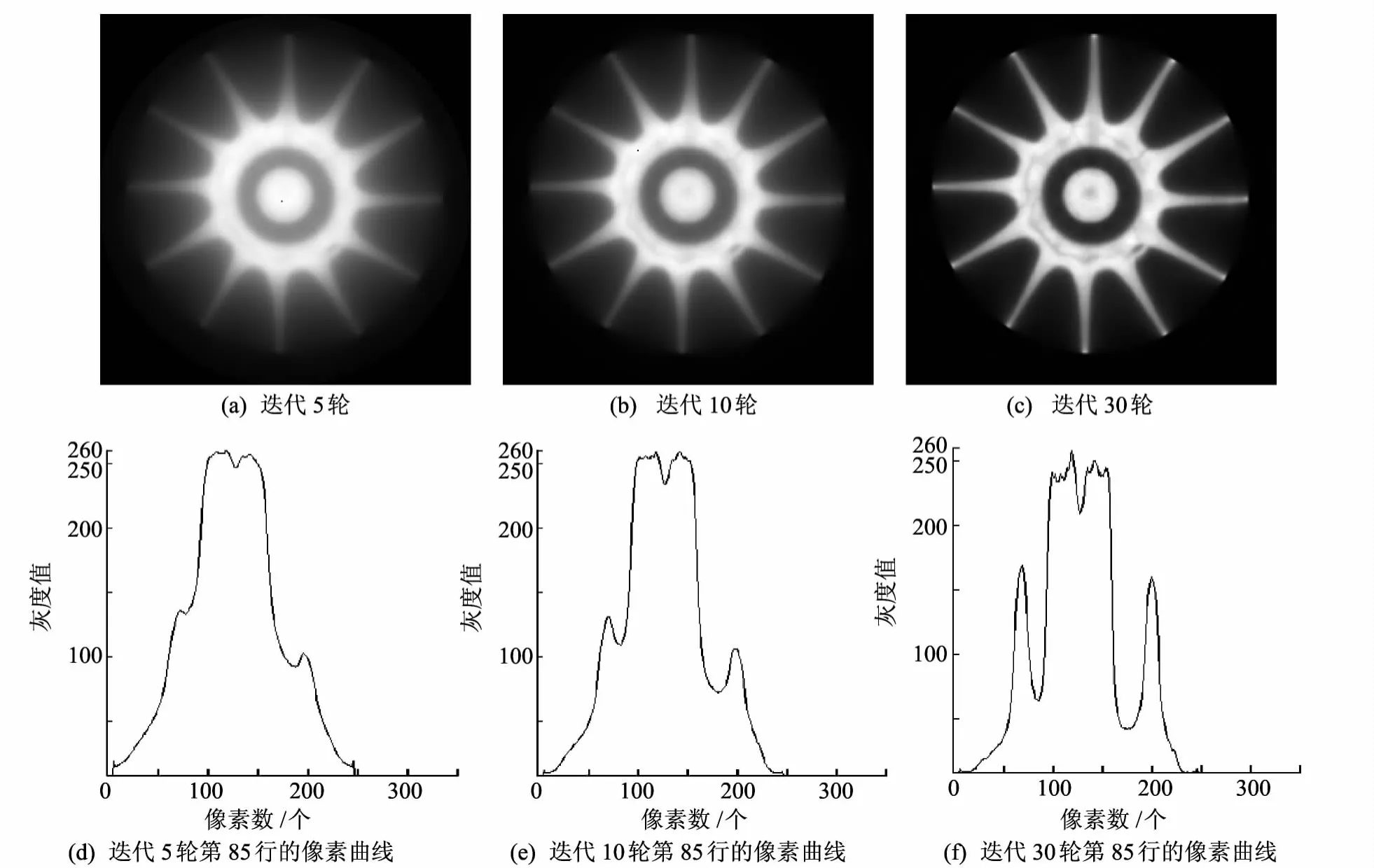
图13 重建点模型加窗基函数EM的重建结果Fig.13 Results of EM with windowed basis function under new discrete model
5 结论
本文用泊松概率模型对发射式断层成像进行了描述,针对传统模型的缺点,引入离散重建点模型.在离散重建点模型中,投影系数矩阵中元素对应着新的物理意义,用重建点到射线的距离的权重来代替原来的截格长度,能更准确地描述线积分的离散表达.
在离散重建点模型中引入了加窗基函数,对该模型进行重构,推导并建立了基于新模型的EM算法,这一迭代重构方法反映了重建模型和扫描模式的本质刻画.实验结果表明算法有效可行.在新模型下,如何选取更为精确刻画投影分布特性的基函数,如何优化和调整迭代构造,深入分析算法的收敛性[10-11],以及建立相应的 OSEM[12-15]算法构造等值得进一步研究,有助于形成应用于实际检测领域的快速实用迭代算法.
[1]Shepp L A,Vardi Y.Maximum likelihood restoration for emission tomography[J].IEEE Trans.Med.Imaging,1982,1:113-122.
[2]庄天戈.CT原理与算法[M].上海:上海交通大学出版社,1992.
[3] Herman G T.Fundamentals of Computerized Tomography:Image Reconstruction from Projections[M].Springer:Second Edition,2009.
[4]刘畅.基于计算点的图像重建离散化模型及其相关算法研究[D].北京:北京信息科技大学,2012.
[5]Lewitt R M.Alternatives to voxels for image representation in iterative reconstruction algorithms[J].Physics in Medicine and Biology,1992,37(3):705-716.
[6]Lange K,Carson R.EM reconstruction algorithms for emission and transmission tomography[J].Journal of Computer Assisted Tomography,1984,8:302-316.
[7] Yan Ming.EM-type algorithms for image reconstruction with background emission and poisson noise[J].Lecture Notes in Computer Science,2011,69(38):33-42.
[8] Teng Yueyang,Zhang Tie.Generalized EM-type reconstruction algorithms for emission tomography[J].IEEE Transactions on Medical Imaging,2012,31(9):1724-1733.
[9]Lewitt R M.Multidimensional digital image representations using generalized Kaiser-Bessel window functions[J].Journal of the Optical Society of America,1990,7(10):1834-1846.
[10] Jiang Ming,Wang Ge.Development of iterative algorithms for image reconstruction[J].Journal of X-ray Science and Technology(Invited Review),2002,10:77-86.
[11]Jiang Ming,Wang Ge.Convergence studies on iterative algorithms for image reconstruction[J].IEEE Transactions on Medical Imaging,2003,22(5):569-579.
[12]邱钧,徐茂林.由投影重建图像的对称块迭代算法[J].电子与信息学报,2007,29(10):2293-2300.Qiu Jun,Xu Maolin.A method of the symmetric block iterative for image reconstruction[J]. Journal electronics& Information Technology,2007,29(10):2293-2300.(in Chinese)
[13]Hudson H M,Larkin R S.Accelerated image reconstruction using ordered subsets of projection Data[J].IEEE Transaction on Medical Imaging,1994,13(4):601-609.
[14]刘畅,邱钧.一种基于对称结构优化的 OSEM快速重建算法[J].CT理论与应用研究,2009,18(4):1-8.Liu Chang,Qiu Jun.An symmetric ordered subset expectation maximization accelerated algorithm[J].CT Theory and Applications,2009,18(4):1-8.(in Chinese)
[15]Dikaios N,Fryer T D.Acceleration of motion-compensated PET reconstruction:ordered subsets-gates em algorithms and a priori reference gate information[J].Physics in Medicine and Biology,2011,56(6):1695-1715.

