结构测试生成中被测电路描述文件转换方法研究

王康谊

(中北大学信息与通信工程学院，山西太原030051)

在数字集成电路测试领域，早期的方法除了需要借助一些常规的普通工具外，最主要还是依靠工程技术人员自身的经验和理论知识，并采取穷举功能的手段来完成测试.这不仅要求技术人员具有较高的业务素质，而且还存在测试速度慢、容易出错、查错麻烦、不宜改动、可移植性差等问题［1-2］.随着集成电路的规模和结构的日益复杂化，现有测试方法所带来的弊端也越来越突出，因此必须寻求新的技术手段来实现对数字集成电路的可靠性测试.近年来兴起的自动测试向量生成(Automatic Test Pattern Generation，ATPG)、内建自测试(Build-In Self-Test，BIST)、边界扫描测试(Boundary Scan Test，BST)和可测性设计(Design For Test，DFT)等先进的测试技术和方法是这方面研究的突出代表［3-5］.其中，自动测试向量生成技术(ATPG)依据一定的测试生成算法，利用计算机对被测电路进行处理，自动生成测试向量，自动加载测试激励并回收输出响应，自动给出故障征兆指示并孤立故障［6］，是对数字逻辑电路进行的一种结构级测试方法.

测试生成算法的执行时间与逻辑电路中门的个数的平方成正比，随着集成电路规模的增大，测试生成算法会越来越复杂，因此研究人员提出了一些迭代算法，常用的如D算法、PODEM算法、FAN 算法和SOCRATES 算法等［3，7］.基于这些算法开发的测试生成软件，比较著名的有美国泰瑞达公司的LASER软件(人们习惯上称为数字电路故障仿真软件)，Mentor Graphics公司的TestKompress和 Synopsys 公司的 TetraMAX［8］，上述软件都是基于UNIX操作系统的付费软件，需要在大型服务器上运行，极大地限制了一般研究人员的使用.因此，根据我国国情和实际需求，开发基于Windows操作平台的“数字集成电路测试生成平台”，在当前具有很重要的现实意义.国内的南京航天航空大学、华中科技大学、华中师范大学等单位都在开展这方面的工作，在测试生成的理论、测试方法学、可测性设计、容错等方向开展了有益的尝试和探索［9-12］.

在“数字集成电路测试生成平台”开发过程中，让计算机识别被测电路是重要的一个步骤.在测试领域，描述被测电路常用的文件有bench，Verilog，VHDL等几种格式，其中bench是官方标准，也是最常用的一种格式.而要用计算机进行结构测试，需要一个统一的格式来描述电路，这就需要把各种格式的电路文件转换成计算机可以识别的网表文件，目前转换成网表文件的方法及网表文件的格式没有官方标准，LASER，Mentor，TetraMax这些著名软件厂商也都有自己的转换方法，并生成一定格式的网表文件，但都未对外公布.通过仔细研究组合逻辑电路自动测试向量生成的典型算法，本课题组发现这些算法都需要知道被测电路中每个节点的属性、级数、扇入数目及具体信息、扇出数目及具体信息、可观测性、0可控制性、1可控制性等，因此提出了下面要介绍的一种网表结构，并命名为lev格式.

本文以bench格式描述的基准电路作为研究对象，探讨把描述组合逻辑电路的bench文件转化为lev格式文件的一些关键技术.

1 问题描述

1.1 bench 文件简介

基准电路是研究测试向量生成算法的模型电路，是由IEEE Circuits and Systems Society推荐使用的标准电路，业内称为 ISCAS(International Symposium on Circuits and Systems)电路，分为组合逻辑电路ISCAS85和时序逻辑电路ISCAS89两大类［3］.基准电路的描述形式不是唯一的，目前常见的有 bench，Verilog，edif，VHDL等多种格式，其中bench格式采用简单的逻辑符号定义基本逻辑门单元，是一种描述门级电路结构的常用方式.

在bench格式所描述的电路中，INPUT代表原始输入，OUTPUT代表原始输出，基本的逻辑门单元则定义为:与门－AND;非门－NOT;NAND－与非门;或门－OR;异或门－XOR;或非门－NOR;异或非门－XNOR;缓冲门－BUF;D触发器－DFF.

下面以最简单的的组合逻辑电路C17为例来介绍bench文件格式.C17中的C表示组合逻辑电路，17表示有17根线，是一个由6个与非门构成的电路，5个输入，2个输出，共有22个单固定故障.其电路示意图如图1所示［3］.

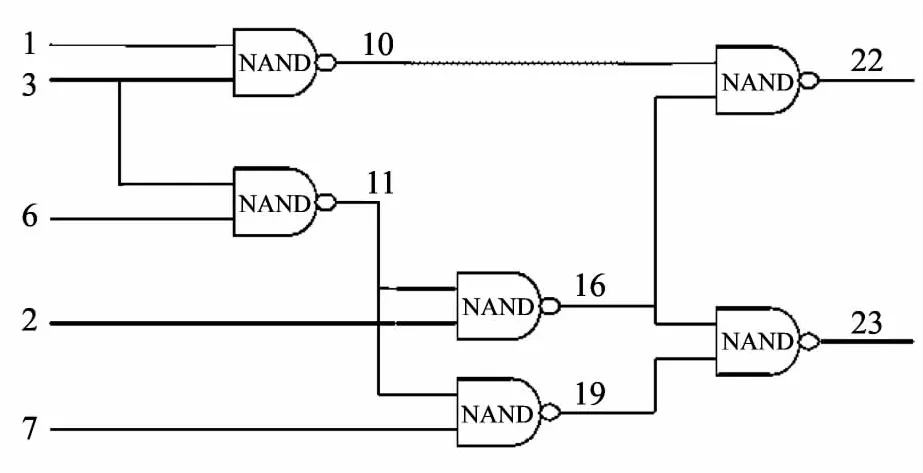
图1 C17电路Fig.1 C17 circuit

c17电路的bench格式描述如下:

其中#为注释部分，记录本电路所有的逻辑门电路的个数.后面为所有输入端和输出端的编号和对每个门电路的描述，如INPUT(1)代表1号端为输入端，11=NAND(3，6)代表一个与非门其输入端为3和6，输出端为11.

1.2 lev 文件简介

lev文件是一个电路网表文件，通过剖析bench格式所描述的电路而生成，并按一定的顺序排列，文件格式如图2所示［9］.

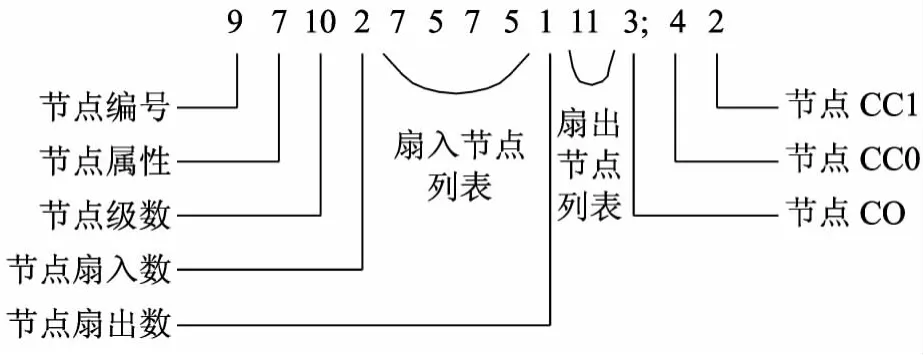
图2 lev文件格式说明Fig.2 Illustration of lev file format

图2的示例中各参数的意义如下:

1)节点编号:电路中的各个逻辑门单元、原始输入和原始输出都被定义为电路节点，并有唯一的编号，每个节点编号在读入 bench文件时安排.

2)节点属性:即节点的类型，用数字来表示，1－INPUT;2－OUTPUT;3－XOR;4－XNOR;6－AND;7－NAND;8－OR;9－NOR;10－NOT;11－BUF.

3)节点级数:规定相邻两级的差为5，即每过一个门电路，节点级数加5.

4)节点扇入数:电路节点的输入端个数.

5)扇入节点列表:与节点扇入数相对应.当节点扇入数为0时，扇入列表不存在;如果不为0，扇入列表会紧跟着出现，并按照可控制性值从小到大排列.为了方便程序读入处理，扇入列表会重复两次.

6)节点扇出数:电路节点的输出端个数.

7)扇出节点列表:与节点扇出数对应，扇出数为0时不存在扇出列表.

8)节点CC0:原始输入节点的0可控制性，默认1.

9)节点CC1:原始输入节点的1可控制性，默认1.

10)节点CO:原始输出节点的可观测性，默认0.

2 Bench文件转化为lev文件的算法实现

2.1 基本数据结构

netlist［］［］:是一个二维数组结构，称为电路网表数组.其中第一维代表电路节点，大小为电路节点的总数;第二维定义了电路节点的逻辑值和各种属性值，包括图2中规定的Lev文件各个参数.特别地，netlist［n］［4］和 netlist［n］［6］指明了节点扇入列表和扇出列表的起始指针.

faninlist［］和 fanoutlist［］:定义了节点扇入列表和节点扇出列表，其起始指针在netlist［］［］中给出，通过寻址就能找到节点n的所有扇入节点和扇出节点.

2.2 算法实现

2.2.1 Bench 转化为 lev的算法

转化算法的基本流程是:逐条读入bench文件的信息，按照Lev格式的规范进行解析，最后生成Lev文件.流程图如图3所示.

图3 Bench转化为lev的算法流程图Fig.3 Algorithm flow chart of bench to lev

2.2.2 电路级数算法

逻辑门的级数涉及到了电路的可测性，定义为从原始输入到达它的各个输入的最大逻辑门距离［13］，本文规定相邻两级之间的差为5，这是为了以后编写生成测试向量程序所做的人为规定，从lev文件表示电路级数的数组中读到0，表示为第一级门，读到5即为第二级门，依次类推.当然也可以采取其它间隔，如10或者15等，甚至间隔为1，只要在程序中设置好即可.流程图如图4所示.

2.2.3 电路可测性算法

数字电路的可测性分析包含两层意思:一个是可控制性，一个是可观测性［14］.可控制性定义为设置特定逻辑信号为0或者1的难度，实际操作中可控制性是指设置输出为0和1的难度，其范围在1和∞ 之间，值越大控制越困难.可观测性定义为观察逻辑信号状态的难度，实际操作中是指输入端的可观测性，其范围在0和∞之间，值越大观测越困难.Goldstein提出了SCOAP可测性度量的概念，规定电路中的每个节点由6个参量来描述［11］:① 组合0可控制性 CC0(Combination Controllability);②组合1可控制性CC1;③组合可观测性CO(Combination Observability);④时序0可控制性SC0(Sequence Controllability);⑤时序1可控制性SC1;⑥ 时序可观测性SO(Sequence Observability).

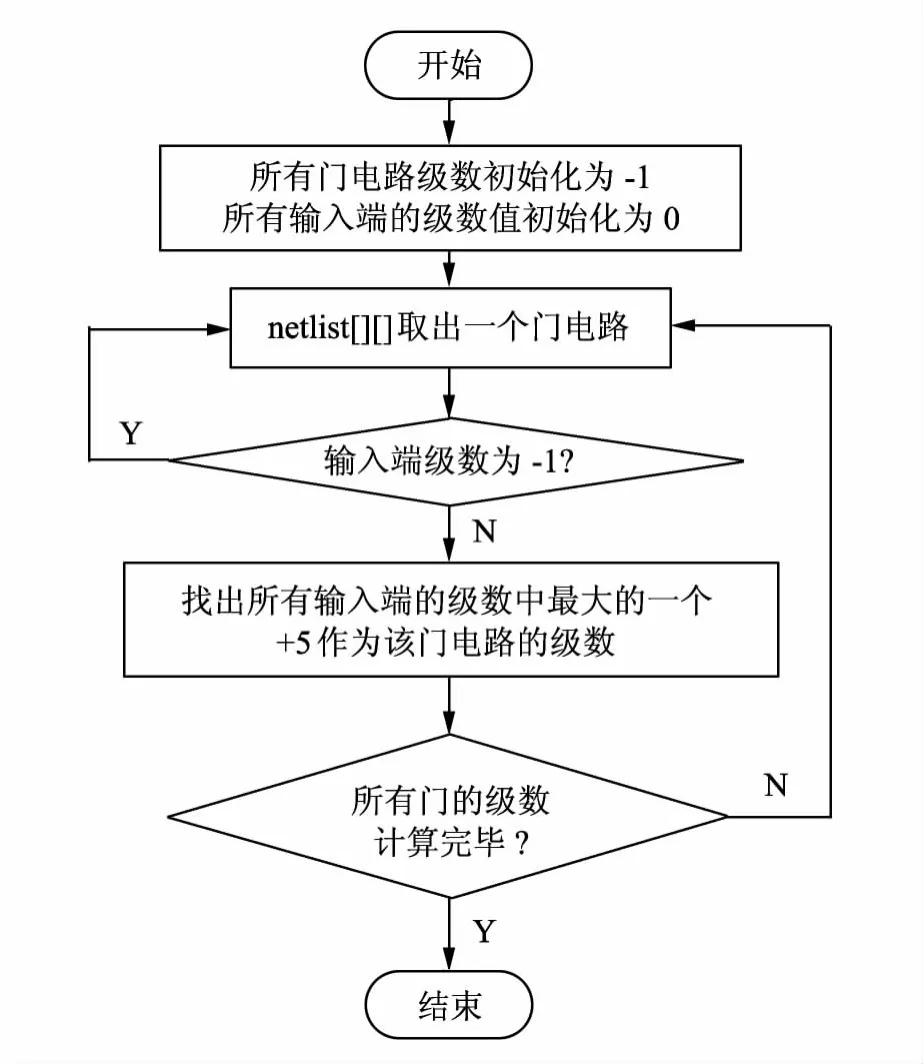
图4 电路级数算法流程图Fig.4 Algorithm flow chart of circuit progression

计算可控制性的方法为:首先设置每个原始输入的CC0和CC1均为1，然后逐级向前通过电路;每经过一个逻辑门，表示逻辑深度增加1，可控制性就加1;如果只设置一个输入就可以生成输出，则输出可控制性等于其中最小的输入可控制性加1;如果需要设置所有的输入才能产生输出，则输出可控制性等于所有输入可控制性之和再加1;如果输出被多个输入集所控制，输出可控制性就等于最小的输入集可控制性加1.根据这个算法，表1列出了全部数字逻辑门的输出节点的可控制性计算公式［9］.

计算出全部输出的可控制性之后，再逆向(从原始输出到原始输入)计算每个输入端的可观测性.首先设置每个原始输出的CO为0，然后选定一个原始输入，计算设置其它输入为非控制值的难度，加上输出的可观测性，再加逻辑深度1，就是该输入的观测难度.依照上述算法，表2给出了全部输入端的可观测性计算公式［9］.

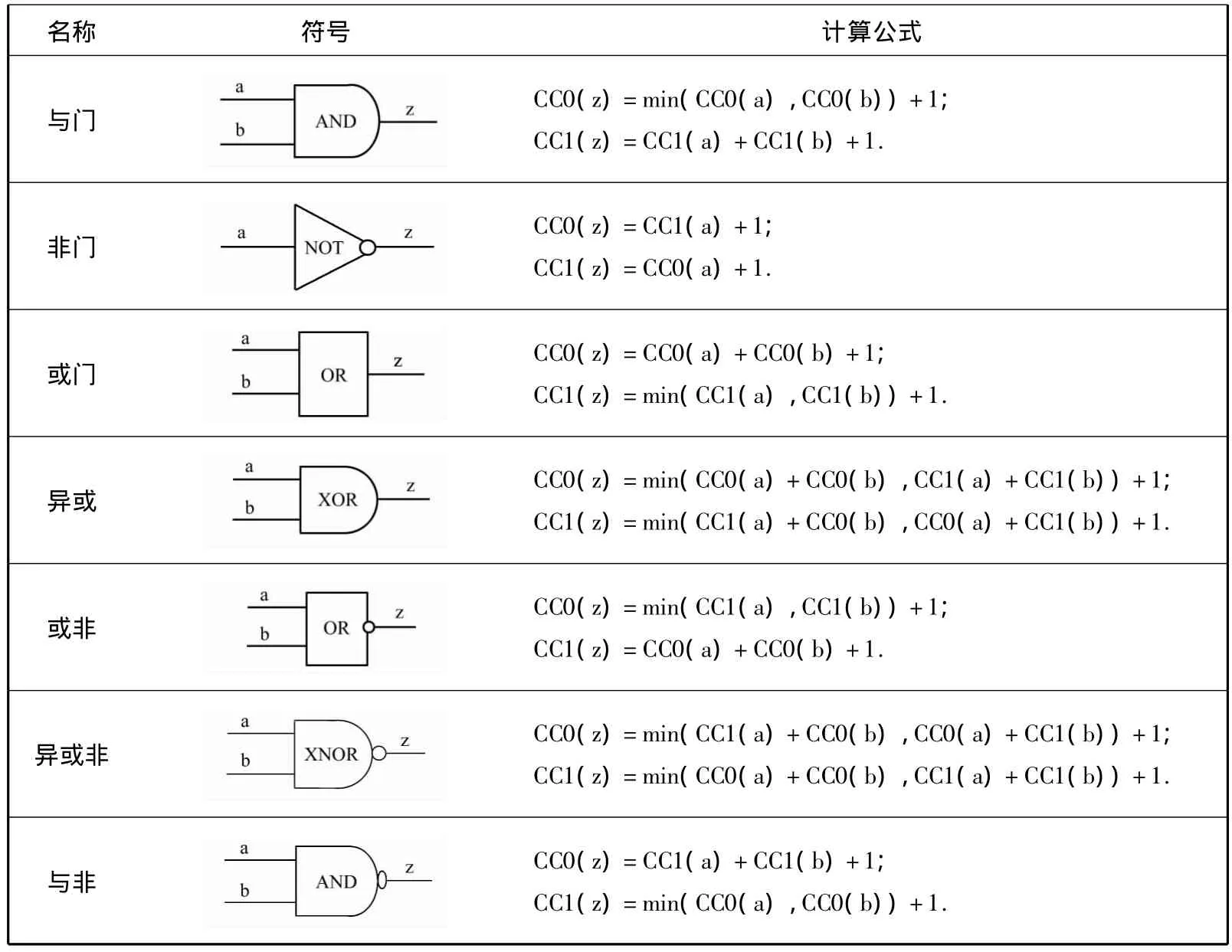
表1 全部数字逻辑门输出节点的可控制性计算公式Tab.1 Calculauion formula of combination controllability of output node of all digital logic gate

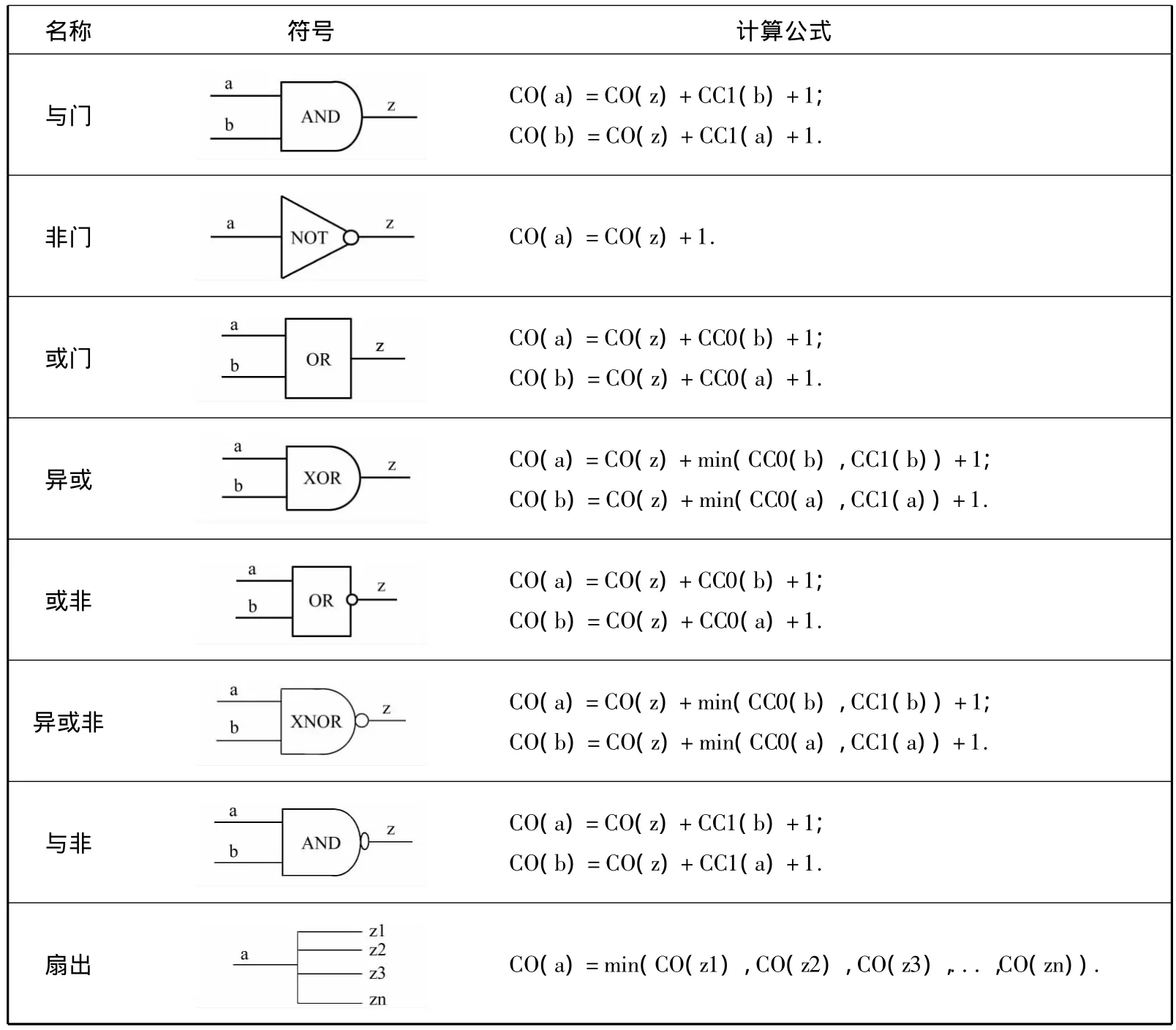
表2 全部数字逻辑门输入端的可观测性计算公式Tab.2 Calculation formula of combination observability of input node of all digital logic gate

由计算方式可知，CC0，CC1和CO这3个组合度量值之间是递归定义的，所以可以采用递归的方式来求解，但是如果电路的个数太多，则效率会大大降低，所以要加入记忆功能，采用记忆化搜索.

电路可控制性和可观测性的算法流程图如图5所示.

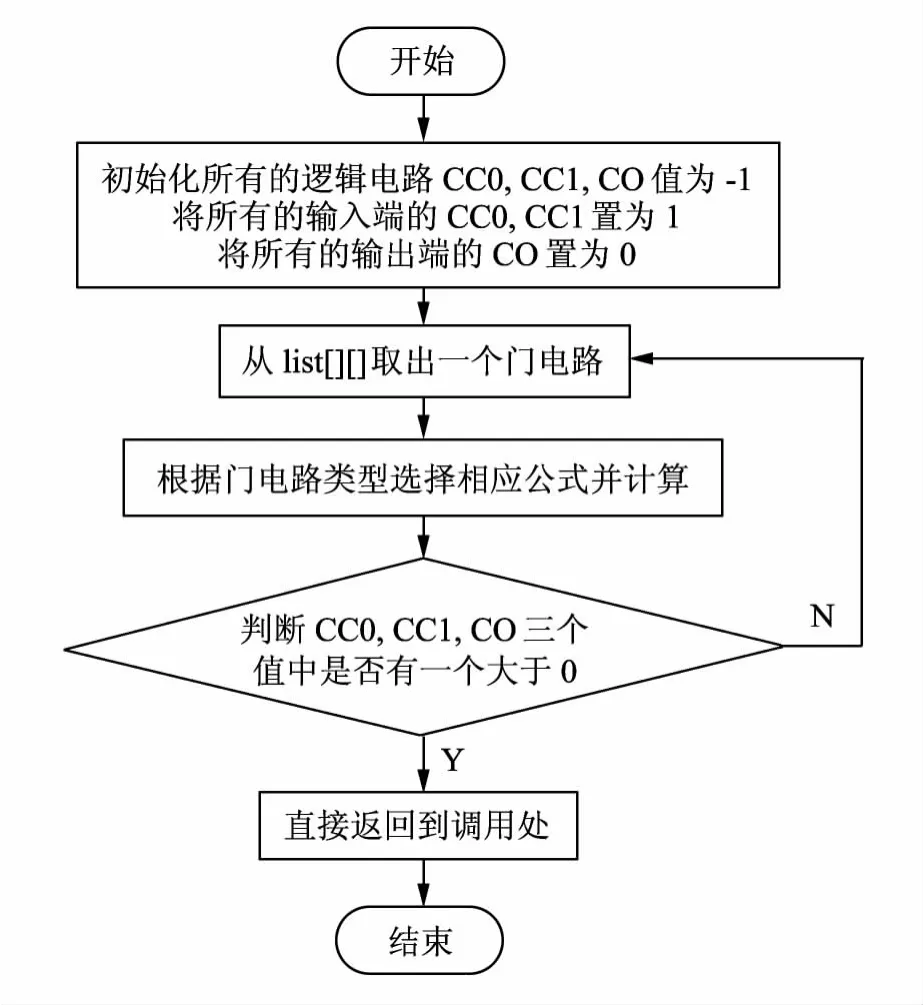
图5 电路可控制性和可观测性计算流程图Fig.5 Algorithm flow chart of combination controllability and combination observability

3 算法验证及结果分析

利用上述算法开发了软件平台，经过测试C17，C432，C499，C880，C1355，C1908，C2670，C3540，C5315，C6288，C7552这11个组合逻辑电路，均可以生成正确的lev格式文件.仍以C17电路为例，所生成的lev文件描述及与bench文件的对应关系为:

3.1 1可控制性、0可控制性、可观测性的算法验证

从前面得到的C17电路的lev文件中得到了各个节点的1可控制性CC1，0可控制性CC0，可观测性CO值，如表3所示.

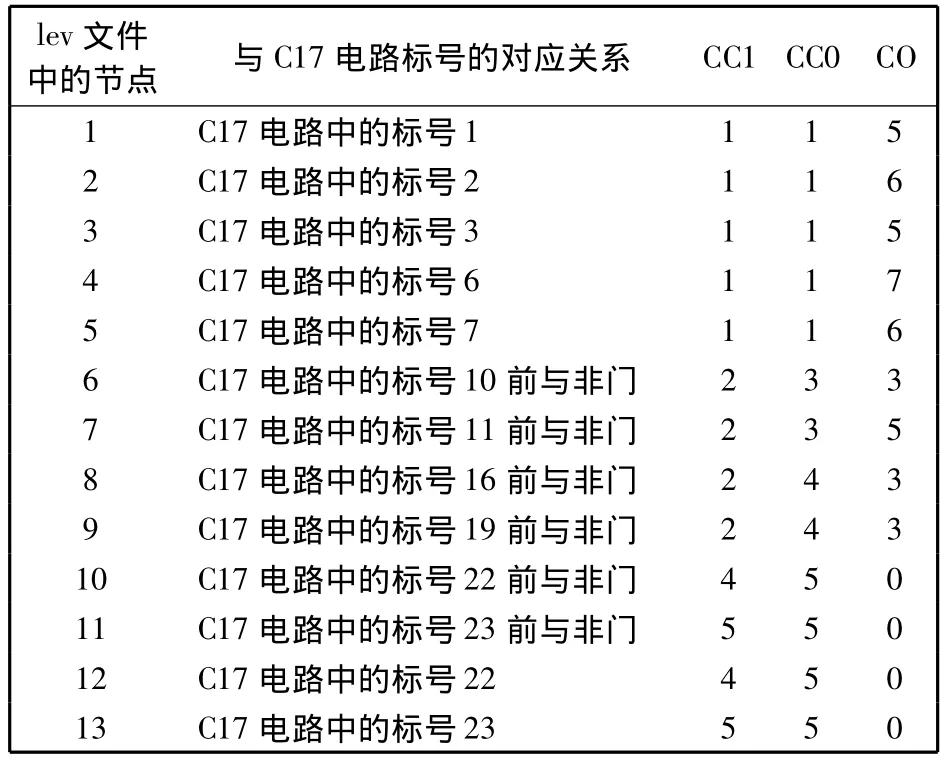
表3 C17电路的节点1可控制性、0可控制性、可观测性值Tab.3 Value of CC1，CC0，CO of C17 circuit

首先来验证1可控制性CC1，0可控制性CC0的正确性.由2.2.3的叙述可知，1可控制性CC1，0可控制性CC0在实际操作中是指设置输出为1和0的难度，值越大控制越困难.从表3中的第3列和第4列数据可以得到:

1)节点离输入端越远越难控制，即节点离原始输入端越远，CC1和CCO应该越大.由C17的电路图可知，表3中节点由上到下的排列顺序正好就是按离原始输入远近排列的，表3的第3列和第4列数值符合这个规律.

2)lev文件中节点6和节点7以及节点8和节点9的可控制值完全相同，这个结果也完全正确，节点6和节点7对应C17中的标号10和11，节点8和9对应C17中的标号16和19，从C17电路图可以看出，标号10和11以及标号16和19处的故障测试难度相同.

3)C17电路全部为与非门，对于与非门，设置输出为1的难度比设置输出为0的难度小，因此对于同一个节点，CC1的值比CC0的值小.表3中第三列和第四数据符合这个规律.

接着来看节点的可观测性数据CO的正确性.由2.2.3中的叙述可知，可观测性在实际操作中是指输入端的可观测性，值越大观测越困难.从表3的第5列数据可以得到:

1)节点离原始输出越远，节点的可观测值CO越大，表3中节点由下到上的排列顺序正好就是按离原始输出远近排列的，表3第5列的数据基本符合这一规律，不完全符合是因为还有接下来2)中的原因.

2)lev文件中节点4的可观测值最大，为7，这个结果也是必然的.从图1可以看出，从原始输出到标号为6处经过的门的个数最多.

3)lev文件中节点2和节点5的可观测值CO相同，为6;节点1，节点3，节点7的可观测值CO相同，为5;节点6，节点8，节点9的可观测值CO相同，为3.这个结果也是必然，节点2和节点5对应图1中的标号2和标号7;节点1，节点3，节点7对应图 1中的标号1，3，11;节点6，8，9对应图1中的标号10，16，19.从图1中可以看出，这些节点的可观测难度应该一致.

以上结果说明本文的可观测性和可控制性算法及程序是正确的.

3.2 其它算法的验证

利用本论文的算法编写程序对前面提到的11个组合逻辑电路进行测试，得到的lev文件应用于后续自动测试向量生成中，与IEEE Circuits and Systems Society提供的测试向量生成结果完全一致［13，15］，进一步说明了其它算法的正确性.图6所示为测试生成平台的运行界面，并展示出了对C432电路的测试结果.由于篇幅关系，对上述其它10个文件未能全部展示.

图6 测试生成平台界面Fig.6 Interface of test generation platform

4 结论

算法验证及结果分析表明，本文所提出的电路描述文件转换方法是有效的，测试结果也证明了算法及程序的正确性.不足之处在于目前所编写的程序还没来得及考虑程序的健壮性问题，这也是下一步需要改进和提高的地方.

［1］薛月菊，王红，杨士元，等.数字电路的层次化测试生成新趋势［J］.哈尔滨工业大学学报，2003，36(11):1281-1284.Xue Yueju，Wang Hong，Yang Shiyuan，et al.New tendency of hierarchical test generation for digital circuit［J］.Journal of Harbin Institute of Technology，2003，36(11):1281-1284.(in Chinese)

［2］成本茂，王红，邢建辉，等.数字电路的高层测试技术及其发展［J］.微电子学，2006，36(2):187-191.Cheng Benmao，Wang Hong，Xing Jianhui，et al.High level testing of digital VLSI circuits and its developing trend［J］.Microelectronics，2006，36(2):187-191.(in Chinese)

［3］Michael L B，Vishwani D A.超大规模集成电路测试——数字、存储器和混合信号系统［M］.蒋安平，冯建华，王新安，译.北京:电子工业出版社，2005.

［4］Michail M，Naghmeh K.Instruction-level impact comparison of RT-vs.gate-level faults in a modern microprocessor controller［C］.USA:27th IEEE VLSI Test Symposium，2009.

［5］刘观生，葛海通，陈偕雄.门级电路自动测试向量生成技术原理［J］.浙江大学学报(理学版)，2006，33(1):52-56.Liu Guansheng，Ge Haitong，Chen Xiexiong.Principles of gated circuit automation test pattern generation［J］.Journal of Zhejiang University(Science Edition)，2006，33(1):52-56.(in Chinese)

［6］Michail M，Naghmeh K.Instruction-level impact analysis of low-level faults in a modern microprocessor controller［C］.USA:IEEE Transactions on Computers，2011.

［7］白玉媛，杨士元，王红.数字电路自动测试生成实用化软件［J］.计算机应用研究，2006(1):174-177.Bai Yuyuan，Yang Shiyuan，Wang Hong.Practical automat ic test generation software for digital circuits［J］.Application Research of Computers，2006(1):174-177.(in Chinese)

［8］邓禹丹.数字电路测试生成平台研究与可测性设计的应用［D］.南京:南京航空航天大学，2007.

［9］刘歆.数字电路的故障测试模式生成方法研究［D］.武汉:华中科技大学，2004.

［10］罗涛.复杂数字电路板的可测性研究［D］.江苏科技大学，2011.

［11］雷绍充，邵志标，梁峰.VLSI测试方法学和可测性设计［M］.北京:电子工业出版社，2005.