矿柱稳定性影响因素敏感性分析及其应用研究
宋卫东 ,曹 帅 ,付建新 ,江国建,吴 锋
(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京 100083;2.北京科技大学 土木与环境工程学院,北京 100083;3.招金矿业股份有限公司 尹格庄金矿,山东 招远 265414)
1 引 言
随着我国地下采矿技术的快速发展和矿山生产能力的逐年提高,高强度采矿必将成为未来发展的主要趋势。然而,矿山地下开采生产能力不断提高的同时,采空区数量及其规模尺寸也急剧增大,一旦采空区发生大面积垮塌,将造成井下严重的设备损坏甚至是人员伤亡事故。因此,实现地下矿山安全高效回采就成为许多矿山企业追求的目标。矿柱对于维持采空区稳定具有极其重要的作用。针对矿柱稳定性的分析主要集中在流变理论研究、模糊可靠度分析及数值模拟等方面[1-4]。姚高辉等[5]通过扩展后的Hoek-Brown 节理强度准则确定岩体力学参数,针对井下矿柱主要破坏形式分别进行了失稳机制分析。王金安等[6]通过矿岩流变特性分析,建立了矿柱支撑下采空区顶板受流变作用位移控制方程。刘洪强等[7]利用断裂力学及突变理论,建立了矿柱失稳的尖点突变模型。江文武等[8]利用简化后的固支梁-矿柱力学模型,得出矿柱失稳只与矿房矿柱自身条件有关,与外界作用无关。罗辉等[9]、赵奎等[10]进行了动态模糊可靠度的矿柱稳定性分析。赵兴东[11]采用FLAC3D数值模拟进行了隔离矿柱稳定性分析。
国内外许多学者在掌握了矿柱稳定性程度的基础上,却较少对影响矿柱稳定性的因素进行重要程度评判,即敏感性分析。本文以招金大尹格庄金矿为例,分析矿柱载荷、强度、破坏形式及影响因素,利用正交试验计算矿柱稳定性安全系数极差,确定相应影响因素敏感性主次顺序。
2 矿柱稳定性分析
采用传统留设矿柱的采矿方法回采矿体时,在一定时间和开采扰动的条件下地应力重新分布而将应力转移到矿柱,因此,本文主要从矿柱载荷、承载强度、失稳形式及影响因素的确定四方面进行矿柱稳定性分析。
2.1 矿柱载荷
正确估算矿柱所受的载荷是矿柱设计的关键步骤之一。国内外就矿柱载荷分析提出了许多假设和分析,包括压力拱理论、有效区域理论、Wilson理论及面积承载理论等。面积承载理论因其计算方法简单易行,使其得到了广泛应用,矿柱的面积承载理论认为矿柱所承受的载荷是其所支撑的顶板范围内上覆岩柱的重力。常见矿柱的布置有连续条带形矿柱(以下简称条形矿柱)和间断式方形矿柱(简称方形矿柱),这里以间断式方形矿柱(认为矿柱长度和矿柱宽度相等)为基本假设进行推导,得到两种形式矿柱载荷公式:
条形矿柱:

方形矿柱:
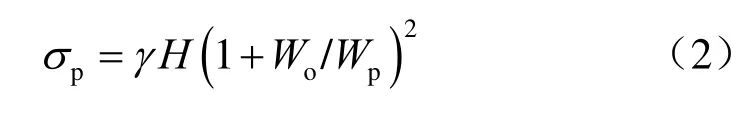
式中:σp为矿柱载荷(MPa);γ为上覆岩层重度(kN/m3);H为矿体开采深度(m);Wo为矿房宽度(m);Wp为矿柱宽度(m)。
2.2 矿柱承载强度
为了计算矿柱的强度,世界各主要采矿国家在试验研究和实例调查的基础上,结合理论分析提出了10 余种矿柱强度计算公式,但大多是对煤矿矿柱的研究结果,对金属矿山矿柱的研究则相对较少。这里采用Lunder 等[12]推导出的考虑矿柱形状效应的精度更高的矿柱强度计算公式:
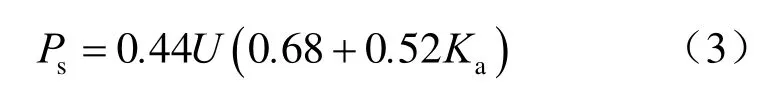
式中:Ps为矿柱强度(MPa);U为矿岩抗压强度(MPa);Ka为矿柱摩擦系数:

式中:Cp为矿柱平均强度系数,取值根据二维边界元模拟分析确定的矿柱宽高比确定:
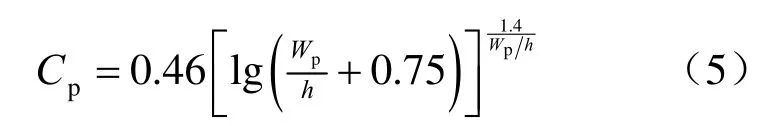
式中:Wp为矿柱宽度(m);h为矿柱高度(m)。
2.3 矿柱失稳形式
矿柱形状及其大小的确定,对于采场的稳定性影响是至关重要的。一般来说,矿柱的破坏主要表现为矿柱表面的剥落、剪切破坏及沿弱节理面的构造破坏等形式[13]。值得注意的是,矿柱在外载荷达极限值时虽可能出现破裂,但并不会立即丧失承载能力。
2.4 矿柱稳定性影响因素确定
影响矿柱稳定性的因素是多方面的,观察载荷和强度计算公式发现,能够定量分析的影响因素有:(1)矿体自身的强度;(2)矿柱自身尺寸,即矿柱宽度和矿柱高度;(3)矿房宽度;(4)矿体开采深度;(5)上覆岩层重度。同时,矿岩本身构造因素影响,即几何缺欠及断层、节理面等,爆破动载对于矿柱稳定性影响也较为显著。
3 矿柱安全系数计算
根据矿柱稳定性影响因素确定结果进行敏感度分析时,为使问题简化,基于矿柱安全系数法,只考虑能够进行定量分析的影响因素,由式(1)~(3)推导出矿柱安全系数计算公式为条形矿柱:
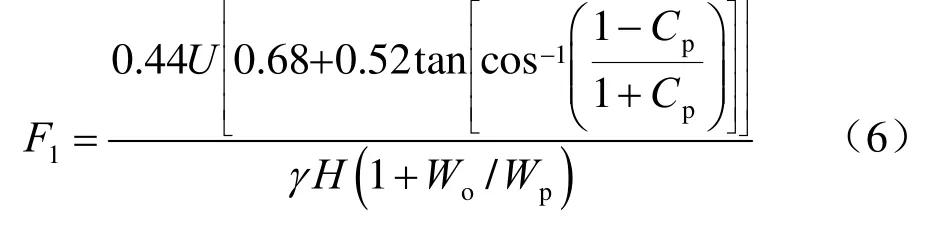
方形矿柱:
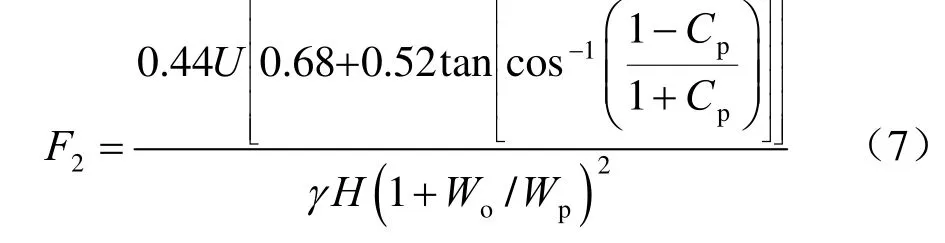
式中:F1为条形矿柱安全系数;F2为方形矿柱安全系数。
4 分析试验方法
由于多因素试验因素间的组合比较多,通常需要耗费大量的精力和经费。正交试验法具有完成试验所需试验次数少、数据点分布均匀等突出特点。用相应的极差分析、方差分析和回归分析等方法对试验结果进行分析,可引出许多有价值的结论,在很多领域的研究中得到广泛应用。本次设计采用正交试验计算矿柱稳定性安全系数的大小,确定各影响因素的敏感性大小。
正交试验开始后,设总影响因素个数为N,序号为i=1,2,…,N,每个因素对应的水平数为M,序号为j=1,2,…,M,构造形如LM2(MN)的正交表,Ki为各因素在同一水平下对应安全系数的平均值。利用直接分析法计算各影响因素的极差Ri,即Ri=maxKj-minKj,i=1,2,…,N;j=1,2,…,M 对比可得各因素的敏感性主次顺序。以某一因素各水平值对试验指标的贡献值为纵坐标,对相应水平值(横坐标)作折线图,能明显看出试验指标随此因素的变化趋势。
5 工程实例分析
5.1 矿山概况
大尹格庄金矿地处招-平主断裂带以下,矿床内赋存1#、2#两个主矿体,其中,2#矿体具有储量大、品位低、倾角缓、中等稳固、矿体较连续等特点。目前,矿区主要采用上向分层点柱式分级尾砂非胶结充填采矿法进行回采矿石。矿房垂直矿体走向布置,盘区长60 m,划分为5个矿块,每个矿块宽12 m,厚度为矿体水平距离。矿房间预留3~6 m间柱不等,阶段高60 m,分段高度为10 m,每分段4个分层,分层高2.5 m,每个分层内根据实际情况,预留方形点柱。分层间回采顺序呈“品”字型布置,2 高左右各1 低。回采自下而上进行,自下盘切割巷开始,沿矿体倾向方向推进,直至矿体上盘边界。回采完成后立即充填,采用废石或分级尾砂充填,充填体与上分层板间留设0.5~1.0 m 的爆破自由面,控顶高度控制在3.5 m 左右,待本分层充填完毕后开始采场联络道的压顶工作,当压顶至分段沿脉巷靠近溜井位置后,进行下一分层的回采作业。
5.2 分析模型的提出
由于胶结充填系统尚未形成,无法胶结充填采空区,未经胶结的尾砂充填体必须经过一段时间养护,待其具有一定强度后,设备及人员才能继续作业。为提高矿区生产能力且最大限度地回收矿石,矿区由原先-140 m 中段单一布置条形矿柱逐步向-380 m 中段条形矿柱+方形矿柱的布置形式过渡,典型采场矿柱布置见图1。在胶结系统形成之前,为尽量减少矿石的损失,矿区计划于-496 m 水平中段不同分段尝试只布置方形矿柱。为简化计算,理想化矿块回采分析模型,见图2。

图1-380 m 四、六分段矿柱分布图Fig.1 Pillar maps of-380 m forth and sixth sublevel
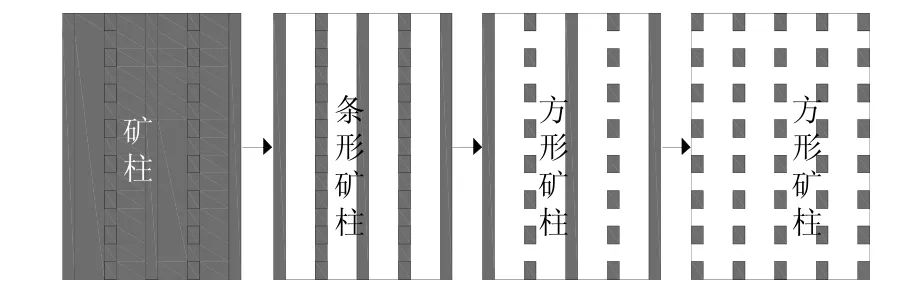
图2 矿块回采分析模型Fig.2 Extraction model of ore blocks
5.3 试验结果分析
根据大尹格庄金矿工程地质及开采技术条件,控制影响矿柱稳定性的6个主要影响因素在适当范围内取值,每个因素取5个水平构造试验设计表(见表1)。为了克服试验偏差,试验开始后对部分影响因素进行随机序列构造试验的水平取值。
以6 因素5 水平构造L25(56)正交试验表,根据式(6)、(7)分别计算单一布置条形矿柱和间断式方形矿柱的安全系数,计算结果见表2。对比发现,相同水平条件下条形矿柱布置要比方形矿柱安全的多;通过极差计算得到条形矿柱影响因素敏感性主次顺序依次为:矿柱宽度>矿体开采深度>矿房宽度>矿岩抗压强度>矿柱高度>上覆岩层重度。很明显,矿柱宽度、矿体开采深度及矿房宽度对矿柱稳定影响最为显著,而矿岩抗压强度、矿柱高度及上覆岩层重度影响程度则相对较弱。绘制两种不同布置形式下矿房宽度、矿柱宽度及矿体开采深度与矿柱安全系数的关系曲线,如图3 所示。
观察表2 发现,矿柱宽度极差达到2.257,矿体开采深度和矿房宽度则分别达到1.261 和0.860,而矿岩抗压强度、矿柱高度和上覆岩层重度极差值均在0.500 以下。为得到安全系数与3个主要影响因素的单一定量关系,研究时将待研究因素作为变量,而固定剩余2个主要因素,避免多因素之间造成的交叉干扰,进而得到矿柱安全系数与上述3个主要因素的定量关系。

表1 影响因素敏感性分析试验设计Table 1 Experimental design for the sensitivity analysis of affecting factors

表2 矿柱安全系数正交试验表Table 2 Orthogonal test of pillar safety factors

图3 矿房宽度、矿柱宽度、矿体开采深度与矿柱安全系数的关系Fig.3 Relationships among room width,pillar width,mining depth and pillar safety factor
5.3.1 矿柱安全系数与矿房宽度的定量关系
为了分析矿柱宽度与安全系数的函数关系,将矿体开采深度和矿柱宽度作为不变量,研究了安全系数随矿柱宽度变化的规律,分别进行了线性拟合、指数拟合及幂函数拟合,得出相应拟合的复相关系数R2的值,拟合结果见表3。
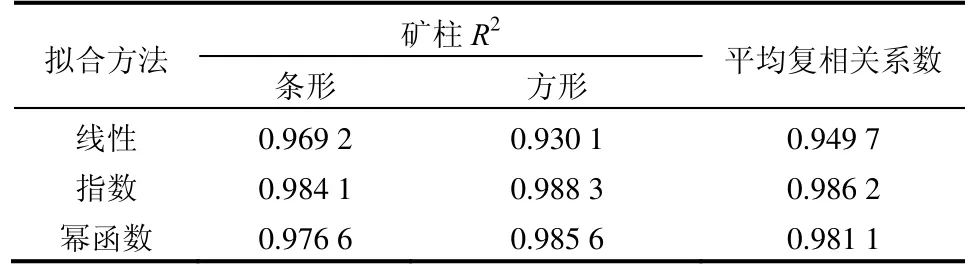
表3 矿房宽度与安全系数定量关系拟合结果Table 3 Fitting results of room width and pillar safety factor
由表3 矿房宽度与安全系数的复相关系数可知,指数拟合的复相关系数达到0.986 2,而幂函数为0.981 1,说明指数拟合更符合矿房宽度对安全系数的影响规律,因此得矿房宽度与安全系数遵循负指数函数y=a1e-b1x的递减规律,a1、b1同时取决于矿柱宽度、矿体开采深度等影响因素。
图4为矿柱安全系数与矿房宽度的指数拟合曲线。由图可见,随着矿房宽度的增大,安全系数值呈指数形式递减且降低速率逐渐变慢。
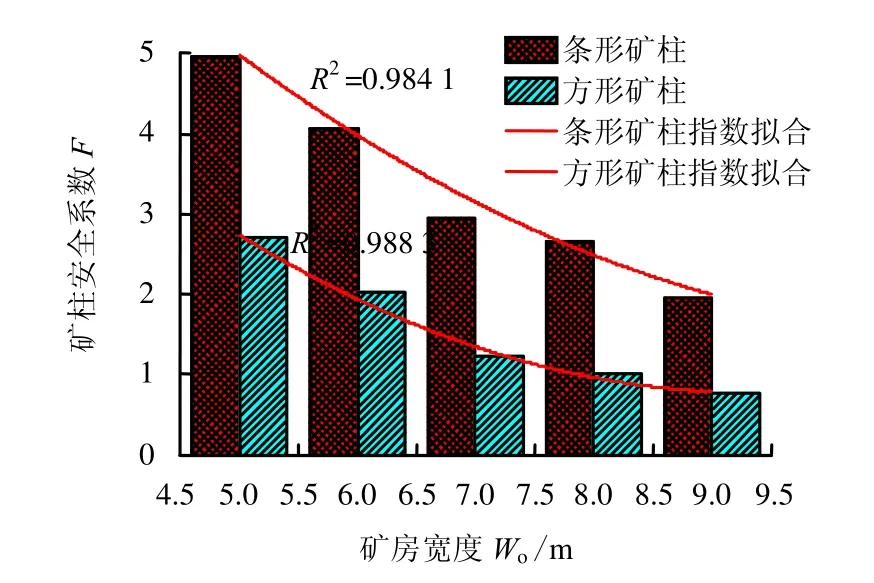
图4 矿柱安全系数与矿房宽度的指数拟合曲线Fig.4 Pillar safety factors and room widths
5.3.2 矿柱安全系数与矿体开采深度的定量关系
将矿柱宽度和矿房宽度作为不变量,研究安全系数随矿体开采深度的变化规律,得到3 种不同拟合方法的复相关系数R2的值,拟合结果见表4。

表4 矿体开采深度与安全系数定量关系拟合结果Table 4 Fitting results of mining depth and pillar safety factor
由表4 可见,幂函数拟合复相关系数达到0.983 6,而指数拟合为0.961 1,说明幂函数拟合更符合矿体开采深度对安全系数的影响规律,由此可得矿体开采深度与安全系数遵循幂函数y=a2x-b2的递减规律,a2、b2同时取决于矿柱宽度、矿房宽度等影响因素。
图5为矿体开采深度与安全系数的幂函数拟合曲线。由图可见,随着开采深度的增大,安全系数逐渐降低且递减速率逐渐变缓。
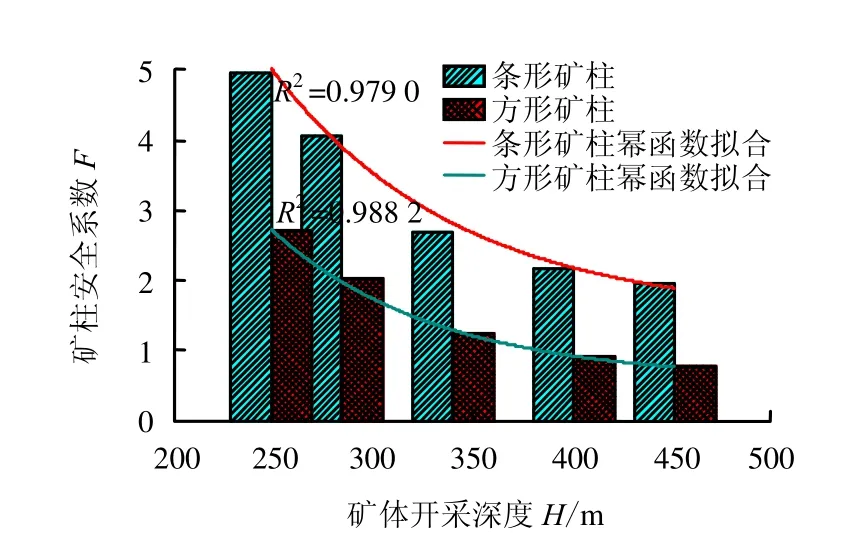
图5 矿柱安全系数与矿体开采深度幂函数拟合曲线Fig.5 Exponential fitting curves of pillar safety factor and mining depth
5.3.3 矿柱安全系数与矿柱宽度的定量关系
采用类似于矿房宽度、矿体开采深度的控制变量法将其余2个主要影响因素矿房宽度和矿体开采深度作为不变量,研究矿房宽度与矿柱安全系数之间的变化规律,计算出相应的复相关系数R2的值,拟合结果见表5。
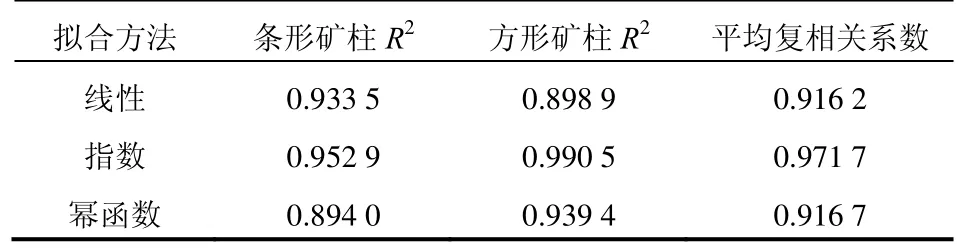
表5 矿柱宽度与安全系数定量关系拟合结果Table 5 Pillar width and pillar safety factor fitting results
由表5 分析矿柱宽度与安全系数的变化规律时发现,只有指数拟合在3 种拟合方法中的复相关系数达到0.96 以上,线性拟合和幂函数拟合分别为0.916 2 和0.916 7,说明指数拟合更符合二者之间的变化规律,由此得到矿柱宽度与安全系数遵循指数函数y=a3eb3x的递增规律,a3、b3同时取决于矿房宽度、矿体开采深度等影响因素。
图6为矿柱安全系数随矿柱宽度变化而变化的指数拟合曲线。由图可以看出,随着矿柱宽度的不断增大,安全系数不断变大且递增速率不断加大。

图6 矿柱安全系数与矿体开采深度幂函数拟合曲线Fig.6 Exponential fitting curves of pillar safety factors and pillar depth
5.4 矿柱安全系数回归方程建立及验证
根据上述分析结果,矿柱宽度、矿体开采深度及矿房宽度对于矿柱安全系数的影响程度最为剧烈。考虑建立一个只包含矿柱宽度、矿体开采深度及矿房宽度3个主要影响因素的安全系数回归方程,为后期采场矿柱布置提供参考依据。常见的回归方法有指数回归、对数回归、幂函数回归及二次多项式回归,经对比采用二次多项式进行回归相关程度最高,通过DPS(DPS 是通用多功能数理统计和数学模型处理数据的软件系统)和Matlab 数据处理软件建立矿柱安全系数与矿柱宽度、矿体开采深度及矿房宽度的回归公式,求得各项回归系数,可直接得到两种矿柱安全系数的回归方程:
条形矿柱:

方形矿柱:

条形矿柱回归方程复相关系数为0.984 4,方形矿柱复相关系数为0.991 3,2个拟合公式的复相关系数均在0.96 以上,能够很好地满足精度要求。为验证方程的可靠性,对大尹格庄金矿-140 m 中段到-380 m 中段采场结构参数进行了统计,代入回归方程得到相对误差见表6。
分析表6 可以看出,回归方程计算所得安全系数与上述推导公式计算值相对误差大部分在6%范围以内,拟合程度高,效果良好,可用于定量预估各种参数条件下的矿柱安全系数,也可以在一定范围内说明矿柱安全系数与矿柱宽度、矿体开采深度及矿房宽度3个主要影响因素的变化关系,因此通过DPS 处理数据软件建立的回归方程是可靠的。
根据Lunder 等[12]所确定的矿柱安全系数1.4,经计算需要满足:矿房宽度不超过8 m,布置条形矿柱宽度不小于3.6 m,与矿区现有布置条形矿柱实际尺寸基本吻合;布置方形矿柱宽度不小于5.9 m。并首次于-496 m 中段4 分段第1 分层布置了每隔6 m 布置了6 m×6 m 的方形矿柱。应用结果表明,相比布置条形矿柱而言能够多回收矿石16.8%,虽然安全性较条形矿柱略差,但整体应用效果较为理想,也为下中段矿体回采时矿柱布置提供了较好的理论依据。
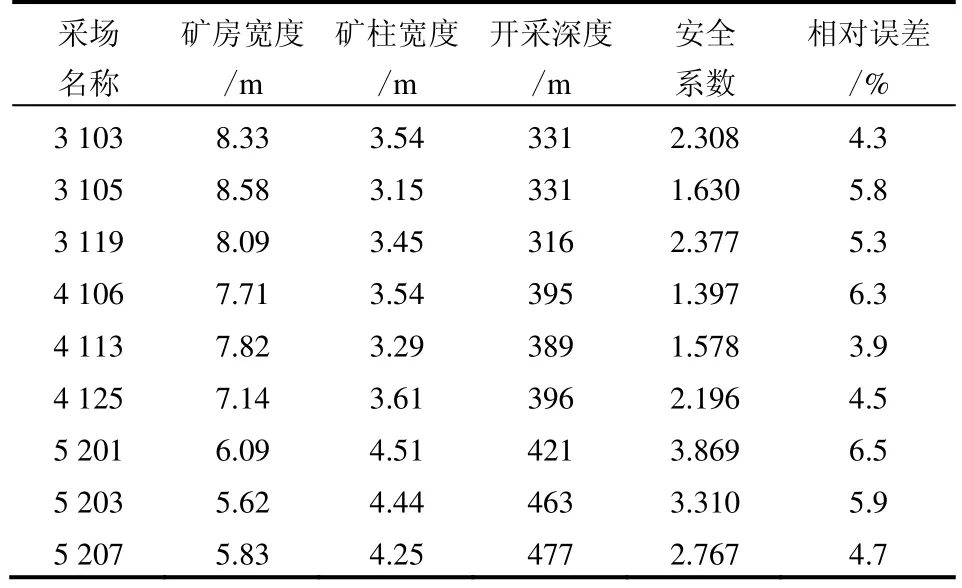
表6-140~-380 m 采场结构参数统计结果Table 6 Statistics of stope structure parameters for-140 m to-380 m
6 结 论
(1)利用正交试验极差,计算得到条形矿柱布置下各影响因素敏感性主次顺序依次为矿柱宽度>矿体开采深度>矿房宽度>矿岩抗压强度>矿柱高度>上覆岩层重度,随着开采深度的不断增大,矿柱宽度及矿房宽度对矿柱稳定性影响最为剧烈。
(2)根据矿房宽度、矿柱宽度及矿体开采深度与矿柱安全系数的关系曲线,矿房宽度与安全系数为指数函数的递减规律;矿体开采深度与安全系数为幂函数的递减规律,矿柱宽度与安全系数则为指数函数的递增规律。
(3)利用DPS 和Matlab 软件建立了只考虑矿柱宽度、矿体开采深度和矿房宽度3个主要影响因素与矿柱安全系数的回归方程,并验证了回归方程的可靠性。得出了保证生产安全的矿柱最小尺寸,即矿房宽度不超过8 m,条形矿柱宽度不小于3.6 m,与矿区现场布置的条形矿柱实际尺寸较为吻合;方形矿柱宽度不小于5.9 m,较条形矿柱而言,提高了矿石回收率,整体应用效果较为理想,也为下中段矿体回采矿柱布置提供了较好的参考依据。
[1]MARTINA C D,MAYBEEB W G.The strength of hard-rock pillars[J].International Journal of Rock Mechanics and Mining Sciences,2000,37(1):1239-1246.
[2]刘沐宇,徐长佑.地下采空区矿柱稳定性分析[J].矿冶工程,2000,20(1):19-22.LIU Mu-yu,XU Chang-you.Stability analysis of pillars in mined-out area[J].Mining and Metallurgical Engineering,2000,20(1):19-22.
[3]邓健,李夕兵,古德生.用改进的有限元Monte-Carlo法分析金属矿山点柱的可靠性[J].岩石力学与工程学报,2002,21(4):459-465.DENG Jian,LI Xi-bing,GU De-sheng.Reliability analysis on pillar structure using a new Monte Carlo finite element method[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(4):459-465.
[4]KRIPAKOV N P,SUN M C,DONATO D A.ADNIA applied towards simulation of progressive failure in underground mine structures[J].Computers &Structures,1995,56(2):329-344.
[5]姚高辉,吴爱祥,王贻明,等.破碎围岩条件下采场留存矿柱稳定性分析[J].北京科技大学学报,2011,33(4):400-405.YAO Gao-hui,WU Ai-xiang,WANG Yi-ming,et al.Stability analysis of stope retention pillars in broken rock conditions[J].Journal of University of Science and Technolgy Beijing,2011,33(4):400-405.
[6]王金安,李大钟,马海涛,等.采空区矿柱-顶板体系流变力学模型研究[J].岩石力学与工程学报,2010,29(3):577-582.WANG Jin-an,LI Da-zhong,MA Hai-tao,et al.Study of rheological mechanical model of pillar-roof system in mined-out area[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):577-582.
[7]刘洪强,张钦礼,潘常甲,等.空场法矿柱破坏规律及稳定性分析[J].采矿与安全工程学报,2011,28(1):138-143.LIU Hong-qiang,ZHANG Qin-li,PAN Chang-jia,et al.Analysis of the failure law and stability of the pillar in open stope mining[J].Journal of Mining and Safety Engineering,2011,28(1):138-143.
[8]江文武,徐国元,马长年,等.基于尖点突变理论的矿房间矿柱的稳定性分析[J].金属矿山,2007,42(9):39-45.JIANG Wen-wu,XU Guo-yuan,MA Chang-nian,et al.Stability analysis of intermittent pillar between stope rooms based on cusp catastrophe theory[J].Metal Mine,2007,42(9):39-45.
[9]罗辉,杨仕教,陶干强,等.基于FEM-ANN-MCS 动态模糊可靠度的矿柱稳定性分析[J].煤炭学报,2010,35(4):551-554.LUO Hui,YANG Shi-jiao,TAO Gan-qiang,et al.Stability analysis of ore pillar and application using concept of dynamic fuzzy reliability based on finite element method-artificial neura network-monte carlo simulation[J].Journal of China Coal Society,2010,35(4):551-554.
[10]赵奎,蔡美峰,饶运章,等.采空区块体稳定性的模糊随机可靠性研究[J].岩土力学,2003,24(6):987-990.ZHAO Kui,CAI Mei-feng,RAO Yun-zhang,et al.Study on fuzzy random reliability analysis for block stability in caved area[J].Rock and Soil Mechanics,2003,24(6):987-990.
[11]赵兴东.谦比西矿深部开采隔离矿柱稳定性分析[J].岩石力学与工程学报,2010,29(增刊1):2616-2622.ZHAO Xing-dong.Stability analysis of insulating pillar of excavation of chambishi copper mine in depth[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Supp.1):2616-2622.
[12]LUNDER P J,PAKALNIS R C.Determination of the strength of hard-rock mine pillars[J].World Mining Letters,1997,14(4):51-55.
[13]尹升华,吴爱祥,李希雯,等.矿柱稳定性影响因素敏感性正交极差分析[J].煤炭学报,2012,37(增刊):48-52.YIN Sheng-hua,WU Ai-xiang,LI Xi-wen,et al.Orthogonal polar difference analysis for sensitivity of the factors influencing the ore pillar stability[J].Journal of China Coal Society,2012,37(Supp.):48-52.

