NSRL 注入器束团长度测量系统初步设计

张 慧 张善才

NSRL 注入器束团长度测量系统初步设计

张 慧 张善才

（中国科学技术大学 国家同步辐射实验室 合肥 230029）

合肥光源注入器升级改造接近完成。为了更好地分析其束流品质，为储存环提供更高品质的束流，针对合肥光源设计了一套利用横向偏转腔(Transverse Deflecting Structure, TDS)测量分析束流纵向品质的系统。利用TDS分析束流纵向品质精度高，功能多样，优势明显。本文TDS采用外围开槽盘荷波导结构，给出了该结构具体尺寸及相关参数计算，并对计算结果做了简要分析处理。根据该结构在注入器的安装位置，对束团长度测量系统进行了物理设计，并分别使用MATLAB程序和PARMELA模拟了束团通过该结构的状态分布，得到了符合预期的纵向束团长度测量结果。

横向偏转腔，盘荷波导，HEM11，MATLAB，PARMELA

随着加速器设计水平及建造技术的发展，束流品质愈来愈好，同时给束流测量技术带来巨大挑战。横向偏转腔(Transverse Deflecting Structure, TDS)是利用射频电磁场直接对束团作用而进行束团纵向特性测量的一种方法。它最初发展于20世纪60年代SLAC的次级粒子束流分离系统[1]。2000年左右，开始应用于电子束流诊断，并曾取得过约30fs的束团纵向测量精度[2]。配合能谱分析系统，可以精确完成单次通过的束团能量分布的测量，即得到其纵向相空间分布。同时，结合四极铁扫描技术还可以测量不同束团纵向位置的水平发射度，即测量束团切片发射度。此外，TDS在压缩同步辐射光脉冲[3]、发射度交换[4]等领域也有应用。总之，TDS是具有优势的一种用于束团诊断的系统，在LCLS、FLASH、SPARC、SPring-8等装置的电子束流测量中已得到广泛应用。

合肥光源(Hefei Light Source, HLS)新一轮的升级改造接近尾声，束流品质将得到显著提高。HLS改造后将要用36nm·rad的双弯铁消色散结构(Double Bending Achromat, DBA)代替现在的160nm·rad的三弯铁消色散结构(Triple Bending Achromat, TBA)。同时改造后将建设一条高性能的直线加速器，实现储存环的满能量注入。实现满能量注入，在条件成熟后，目标是实现准恒流运行模式(Top-Up)。届时将可在更低的发射度、更高的流强以及更稳定的光束品质下运行。为了更好地配合实验室将来的发展，更加精确地优化直线加速器参数，提高准恒流运行模式的注入效率。本文针对合肥光源注入器设计了一套束团长度测量系统。该系统利用一种较新颖的TDS腔结构实现了束团纵向与横向之间的相空间变化，能够直观地测量束团长度。本文介绍了该结构应用于束团长度测量的相关理论、计算、模拟等内容，具体结构安排有以下4方面：(1) TDS工作原理介绍，包括工作场型的简要分析，束团长度测量的理论依据；(2) TDS单腔的尺寸设计及相关参数的计算分析；(3) 基于薄透镜模型，束流通过该结构的MATLAB模拟分析；(4)利用PARMELA模拟计算了该结构对束流的作用。

1 TDS工作原理

1.1场型分析及偏转电压

根据电磁波的工作状态，TDS分为行波结构与驻波结构。两种结构各有优劣[5]，但其内描述粒子在射频(Radio-Frequency, RF)场中横向偏转的基本理论均是Panofsky-Wenzel定理[6]，其表达式如下：

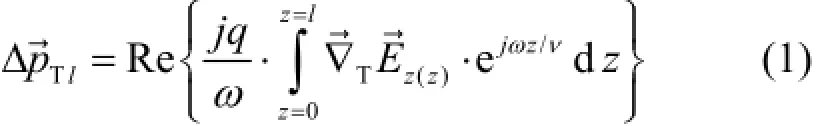
式(1)说明：在长度为l的TDS结构中，粒子从电磁场获得的总的横向动量是与纵向电场的横向梯度成比例的。因此，纯横电波(Transverse Electric wave, TE)不会对粒子产生横向偏转。经进一步分析：对于行波结构，横磁波(Transverse Magnetic wave, TM)的TM11模式对极端相对论性粒子的偏转力也为零。因此，为了使用行波结构偏转高能粒子，必须建立混合模式电磁波。实际上，行波结构中工作的电磁波是混合电磁波(Hybrid Electromagnetic wave, HEM)的HEM11模式，它是由TE11与TM11波模叠加而成的混合波，TE11与TM11波相互耦合，不能在盘荷波导中单独激励、单独传播。

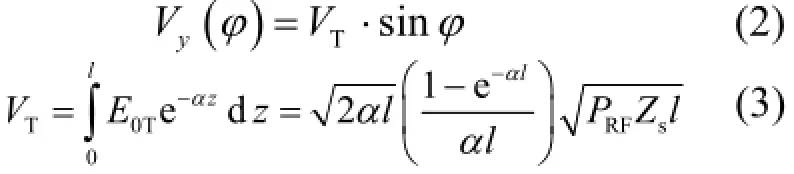
本文研究等阻抗行波偏转结构，粒子为极端相对论电子。假定偏转方向为垂直方向(y)，定义偏转电压为单位电荷所受横向偏转力在腔内的积分。理想情况下，其表达式[7]：式中，VT表示偏转电压峰值；E0T是功率馈入口等效横向偏转场峰值；φ=φ0-kz是粒子进入偏转腔时对应的微波场相位；φ0是中心参考粒子的相位，我们通常调节使0φ=0，即过零相位；α为电场衰减常数；PRF为馈入微波功率；l偏转腔长度；Zs为单位横向分路阻抗。

1.2束团纵向尺寸计算与分辨率

TDS对沿z方向运动束团的作用见图1[8]。如图1所示，当偏转腔工作时，束团处于合适的相位上，偏转电压在束团的中心为零，束团前后不同纵向位置的粒子受到不同的横向力的作用，其大小与其相对束团中心的距离成线性关系。束团通过横向偏转腔后，会沿着束团纵向产生一个线性的y方向的角动量的分布。在偏转腔后面一定距离的接收屏上，这个正比于束团纵向位置的角动量的分布会转化为y方向的横向位移。因此，在屏上y方向的束团尺寸就会反映出束团的纵向信息。

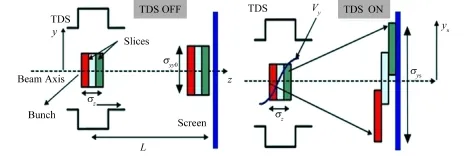
图1 TDS对运动束团的作用Fig.1 Evolution of the bunch in TDS.

束团长度用zσ表示，忽略束团垂直方向发射度，则屏上纵向束团偏转的最大位移表示为[9]：

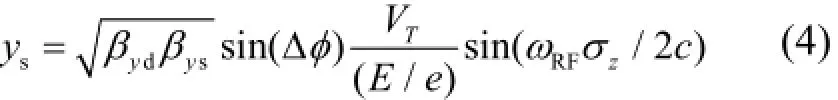
式中，βyd和βys分别是偏转腔中心与屏位置处的β函数；φΔ是偏转腔中心与屏之间β函数的相位差；ωRF是偏转场角频率；σz为束团纵向尺寸均方根值；e为电子电荷量；E为束流的能量，eV。

当λ＞＞σz时，考虑简单情况即偏转处与接收屏之间仅存在长度为L的漂移段，则式(4)可简化为：

式(4)、(5)表明：纵向束团的分布可以通过测量经过偏转腔之后的横向束团分布来实现。

接收屏上束团分布是纵向束团偏转的总位移与屏处束团垂直尺寸的耦合，则其大小syσ可表示为：

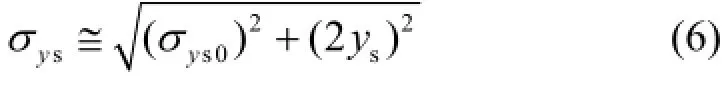
束团长度分辨率(resL)定义为：经TDS系统偏转后到达屏上的束团总位移(s2y)刚好等于未加偏转电压时屏上垂直束斑大小(s0yσ)的值时，所对应纵向束团长度的值。对于漂移段情况，由式(5)可以得到束团长度分辨率的表达式为：

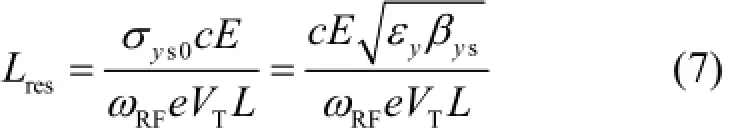
式中，yε为偏转方向的横向发射度大小。由式(7)知，syβ越小，分辨率resL越高。

2 单腔结构的设计及计算分析

本文研究等阻抗行波偏转结构，其本质是一等阻抗盘荷波导。对盘荷波导的研究方法，主要有等效电路法和场分析法。本文使用计算机模拟的场分析方法研究，设计基于的工具是CST-WS软件。

HEM11模是偶极模，它在偏转结构中存在极化简并现象。对于普通盘荷波导，其结构很小的不均匀度可能导致极化场极化方向的旋转，从而降低偏转效率。因此，必须采取稳模措施。常用的稳模措施有三种：(1) SLAC使用盘片两边附加的对称开孔来稳模[10]；(2) SPARC采用安装穿过盘片的两个对称金属细棒来稳模[9]；(3) SPring-8通过跑道型盘片开孔设计来稳模[11]。借鉴莫斯科工程物理研究所的设计[7]，我们采用一种较新的稳模方式——内壁对称开槽结构。较之前三种结构，该结构具有建模简单、加工组装方便、边界场强低等优点。其单腔具体结构见图2。

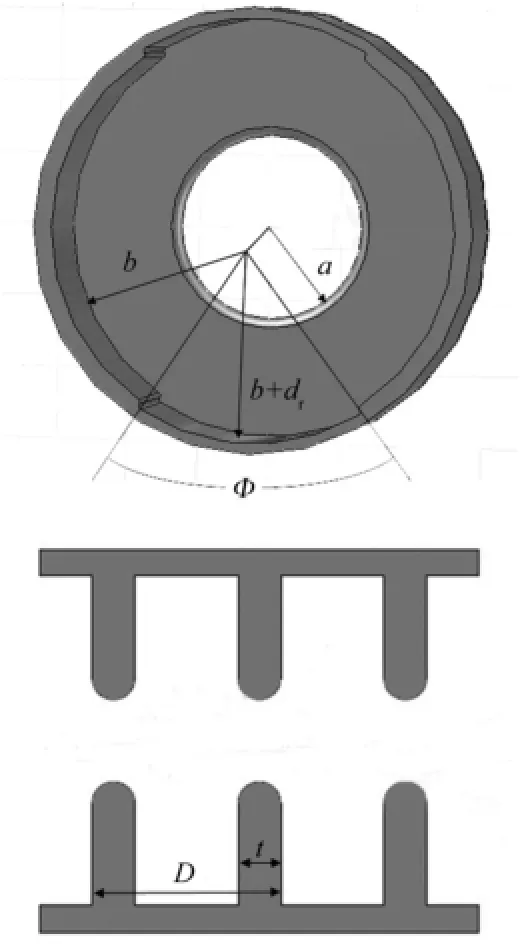
图2 单腔结构a–盘片内径，b–圆柱腔内径，t–盘片厚度，D–单腔长度，dr–开槽厚度，Φ–开槽角度Fig.2 Single cell structure. a–iris radius, b–internal radius, t–iris thickness, D–cell length, dr–recess thickness, Φ–recess angle

经多次计算比较，一组满足我们需要的偏转结构尺寸参数为：D=34.99 mm，b=57.05 mm，a=25.50mm，t=5.00 mm，dr=1.00 mm，Φ=65°。

由这组数据在CST软件MICROWAVE STUDIO模块中建模，计算得到该结构工作模式的相关射频参数：f=2856.43MHz，Zs=14.2MΩ·m-1，α=0.136m-1，Q=12997，相对群速度gβ=-0.0168，φ=2π/3。

偶极场简并模式中，腔中心轴附近电场方向与开槽方向相同的极化定义为垂直极化；相应的，腔中心轴附近电场方向与开槽方向垂直的极化称为水平极化。经CST计算，本设计结构腔内垂直极化电磁场场型分布见图3（以0相位为例）。由此场型可知：当调节电子束团相位使之中心与垂直极化场零点相重合时，束团将会产生如图1所示的偏转。模拟计算显示：场的最大值在盘片倒角附近而边壁处场强较弱。

图3 电场(a)：左为+z向视图，右为+x向视图磁场(b)：左为+z向视图，右为+y向视图Fig.3 Electric field: the view of +z direction on the left hand and the view of +y direction on the right hand (a), magnetic field: the view of +z direction on the left hand and the view of +x direction on the right hand (b).

采取内壁凹槽稳模措施后，带来的频率分离情况见图4。由图4可知，有稳模措施时水平极化偏转场频率与无稳模时偏转场频率接近且略有下降，而此时垂直极化偏转场频率却比无稳模时偏转场频率下降较多。该稳模措施大约可使两个极化模式在2π/3处获得25.5MHz的频率分离，足够满足偏转腔的稳模需求。

为了进一步优化的方便，还计算了单腔的主要特征尺寸误差对极化频率的影响(见图5)。由图5可知，在小尺寸调节范围内，腔尺寸变化与工作频率变化是成线性关系的；除t以外，a、b、dr、Φ等参数变化均与频率变化负相关；b的影响最大，当频率相差太远时，优先考虑调节b。同时发现，对于垂直与水平极化情况，dr的影响差异很大。这是容易理解的，因为对于垂直极化dr的影响相当于b的影响，而水平极化并非如此。

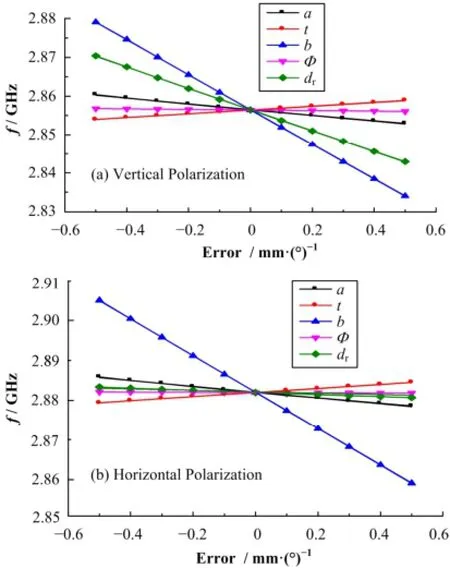
图5 腔的特征尺寸误差对极化频率的影响Fig.5 Characteristic dimension error impact on polarization frequency.

3 基于薄透镜近似理论的MATLAB模拟

为了直观了解电子束流经过该腔结构的状态，利用基于薄透镜近似的传输矩阵理论编写MATLAB程序对该结构进行了模拟分析。

偏转腔薄透镜近似，即偏转腔的作用可以视为由其中心的当地激发而产生的单次剪切力来近似描述。基于此近似，可以得到偏转结构的（）,,yyz′三维传输矩阵为[12]：

考虑长度为L漂移空间，则偏转结构与漂移段的（y,y′,z）三维总传输矩阵为：

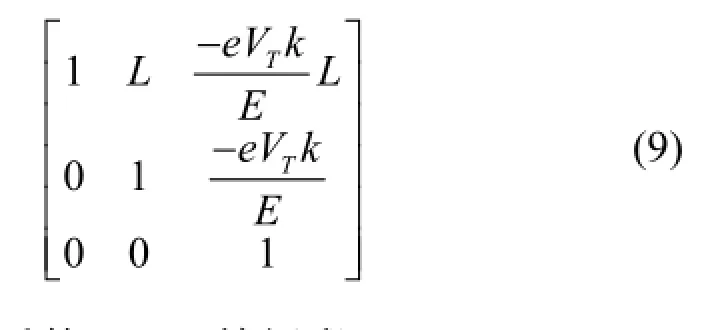
对于升级后的HLS输运段，E=800 MeV，εy=25.55 nm·rad，考虑直线节空间限制，将接收屏位置选定在距直线加速器出口28.607 m处，此处βys=2.537 m。欲由式(7)得到Lres=1 ps，可以选择：VT=5 MV，L=2.268 m。代入以上数据，矩阵(8)、(9)分别为：

偏转腔中心位于距加速器出口26.339m处，可计算得出此处的初始束团垂向尺寸均方根值与发散角均方根值、束团纵向尺寸均方根值分别为：σyd0=0.344 mm，σy'd0=0.074 3 mrad，σz=3 mm。

考虑理想简单情况，利用MATLAB软件随机生成服从高斯分布的粒子10000个，分别对经过偏转结构与经过漂移段后的束团在(,)yz、(,)yy′二维相空间的分布进行模拟，结果见图6。

由计算结果可知：如图6(a)所示，束团经偏转腔作用之前在(,)yz与(,)yy′相空间均呈标准高斯分布且y与y′均不大；如图6(b)所示，束团经偏转腔作用之后(,)yz相空间几乎没有变化，但(,)yy，相空间y′明显增大，这是y′分布受横向电磁场作用的结果，同时y、z的分布并未有受到显著影响；如图6(c)所示，在接收屏上，(,)yz与(,)yy′相空间均因y分布的增长发生倾斜，显然是由于束团经漂移段之后y′分布转化为y的分布的缘故。此时，束团纵向特性z已可以通过横向特性y的测量表示出来。

4 PARMELA模拟

欲获得5MV的偏转电压，利用式(3)，可以选择：馈入功率为10MW，偏转结构总长度为0.852m。把CST计算的三维电磁场导入PARMELA，设定粒子初始参数与MATLAB模拟参数基本一致，得到束团在进入TDS之前、离开TDS之后及接收屏上的(,)yφΔ、(,)yy′二维相空间图见图7，其中φΔ与z的换算关系约为0.29mm·(°)-1。

图7反应得出，束团从TDS入口到出口，最后到达接受屏上的过程中，相空间的总体变化趋势与MATLAB的模拟是一致的，分析造成相空间如此演化的原因也是相同的。图7(b)与图6(b)差异较大，主要原因是在PARMELA模拟中，粒子通过TDS结构时，由于结构本身有一定的长度，随着y′在垂直极化场的作用下发生线性变化，y也相应地发生了线性增加。而在MATLAB模拟中，TDS采用了薄透镜近似，忽略了TDS结构本身长度，也因此忽略了在结构内的横向偏移。因此在TDS出口处，图7(b)中的相图发生了偏转，而图6(b)中没有。这正是图7(c)中屏上y值略大于图6(c)中y值的主要原因。

图6 TDS作用之前(a)、作用之后(b)和接收屏上(c)相图Fig.6 Phase space before TDS effect (a), after TDS effect (b) and at the screen (c).

图7 TDS作用之前(a)、作用之后(b)和接收屏上(c)相图Fig.7 Phase space before TDS effect (a), after TDS effect (b) and at the screen (c).

5 结语

本文完成一种适于合肥光源参数的TDS腔结构设计，给出该结构具体尺寸及相关参数结果分析。选取外围开槽设计，具有建模简单和加工组装方便，可以产生约25.5MHz的频率分离，足够满足稳模的需要。文中分别利用MATLAB与PARMELA模拟了束团通过该结构的状态分布。给出了束流到达接收屏时束团在(y,z/Δφ)与(y,y′)相空间中的状态分布情况，两种模拟结果符合较好。该设计完全可以满足对合肥光源直线加速器纵向束团参数测量的需求。结合能谱分析系统与发射度测量系统将可以对束团做更细致的测量，相关工作正在进行中。

1 Altenmueller O H, Larsen R, Loew G A. Investigations of traveling wave separators for the Stanford two mile linear accelerator[J]. Review of Scientific Instruments, 1964, 35: 438–442

2 Berden G, Gillespie W A, Jamison S P, et al. Benchmarking of electro-optic- monitors for femtosecond electron bunches[J]. Physical Review Letters, 2007, 99: 164801

3 Zholents A, Heimann P, Zolotorev M, et al. Generation of sub-picosecond X-ray pulses using RF orbit deflection[J]. Nuclear Instruments and Methods in Physics Research, 1999, A425(1-2): 385-389

4 Emma P, Huang Z, Kim K J, et al. Transverse-tolongitudinal emittance exchange to improve performance of high-gain free-electron lasers[J]. Physical Review St Accelerators and Beams, 2006, 9: 100702

5 Alesini D. RF deflector based sub-ps beam diagnostics application to FEL and advanced accelerators[J]. International Journal of Modern Physics A, 2007, 22: 3693–3725

6 Panofsky W K H, Wenzel W A. Some considerations concerning the transverse deflection of charged particles in radio-frequency fields[J]. Review of Scientific Instruments, 1956, 27: 967–967

7 Sobenin N, Lalayan M. Stabilization of the polarization plane in travelling wave deflectors[C]. Proceedings of IPAC’10, Kyoto Japan, 2010: 3759–3761

8 Alesini D. Sliced beam parameter measurements[C]. Proceedings of DIPAC09, Basel, Switzerland, 2009: 146–150

9 Alesini D. RF deflector design and measurements for the longitudinal and transverse phase space characterization at SPARC[J]. Nuclear Instruments and Methods in Physics Research, 2006, A568: 488–502

10 Akle R. A transverse RF deflecting structure for bunch length and phase space diagnostics[C]. SLAC-PUB-8864, June 2001

11 Ego H, Otake Y. Design of the transverse C-band deflecting structure for measurement of bunch length in X-FEL[C]. Proceedings of EPAC08, Genoa, Italy, 2008: 1098–1100

12 Korepanov S, Krasilnikov M, Alesini D, et al. An RF deflector for the longitudinal and transverse beam phase space analysis at PITZ[C]. Proceedings of DIPAC, Venice, Italy, 2007

CLCTL53

Preliminary design of the bunch length measurement system for NSRL injector

ZHANG Hui ZHANG Shancai
(National Synchrotron Radiation Laboratory, University of Science and Technology of China, Hefei 230029, China)

Background:With the development of design and construction technology in accelerator fields, high-quality beam brings challenges to beam diagnostics.Purpose:To meet the strict requirements, new beam measurement techniques have emerged. One of them is the Transverse Deflecting Structure (TDS) method that possesses advantages of versatility and high precision. This paper aims to design a TDS Structure for longitudinal measurements.Methods:Based on the work on TDS by scientists around the world, the Computer Simulation Technology-MICROWAVE STUDIO (CST-WS) software was applied to design a TDS cell structure-Disk loaded waveguide structure with two peripheral recesses matched to Hefei Light Source (HLS) parameters. Beam dynamics simulations are executed by using MATLAB and PARMELA to show the evolution of the bunch distribution in the structure, respectively.Results:Dimensions of this TDS, the field type and the resulting dispersion curve are obtained. And the impacts on the operating frequency of feature sizes are explicated. Conclusion: This structure can get the desired deflection field type. Stabilizing mode method can realize stable ～25.5 MHz frequency separation, which can be proved effective through CST simulations. Characteristic dimension b impacts the operating frequency most, and drimpacts changes most for different polarization modes. MATLAB and PARMELA simulation are consistent.

Transverse Deflecting Structure (TDS), Disk loaded waveguide, HEM11,MATLAB, PARMELA

TL53

10.11889/j.0253-3219.2014.hjs.37.090101

张慧，男，1989年出生，2011年毕业于西南科技大学，现为中国科学技术大学硕士研究生，核技术及应用专业

张善才，E-mail: shancai@ustc.edu.cn

2014-03-03，

2014-04-08