鲟鱼中荧光假单胞菌生长预测模型构建及货架期预测
章志超,桂 萌,彭朝辉,李平兰,*
(1.中国农业大学食品科学与营养工程学院,北京 100083;2.北京北水食品工业有 限公司, 北 京 100068)
鲟鱼中荧光假单胞菌生长预测模型构建及货架期预测
章志超1,桂 萌1,彭朝辉2,李平兰1,*
(1.中国农业大学食品科学与营养工程学院,北京 100083;2.北京北水食品工业有 限公司, 北 京 100068)
为快速预测有氧贮藏鲟鱼的货架期、预防鱼肉变质,通过将鲟鱼有氧冰藏条件下的特定腐败菌(荧光假单胞菌)接种于灭菌鲟鱼片后置于0、4、10、15、20 ℃有氧贮藏,分析其生长动态及货架期终点的感官评分、pH值和挥发性盐基氮值,在以修正的Gompertz方程为一级模型的基础上,分别以平方根方程和Arrhenius方程为二级模型,建立 并验证荧光假单胞菌 的生长预测模型。结果显示:荧光假单胞菌菌数的最小腐败值为(7.35±0.05)(lg( CFU/g));同时,分别在8 ℃ 和波动温度 条件下对模型验证的结果表明:基于平方根方程的荧光假单胞菌生长预测模型的残差分布在- 0.09~0.10之间,准确度Af为1.14、1.17,偏 差度Bf为 0.97、1.02,货架期预测相对误差为-7.95%、-3.28%;而基于Arrheni us方程的模型误差较大,其中残差分布在-0.17~0.24 之间,Af为1.21、1.31,Bf为0.94、1.08,货架期预测相对误差为24.87%、7.54%。因此,基于平方根方程建立的模型可以更有效地预测有氧包装鲟鱼在0 ~20 ℃贮藏温度条件下的荧光假单胞菌的生长及相应货架期。
鲟鱼;荧光假单胞菌;温度;预测模型;货架期
鲟鱼是世界上一种最古老的中大型淡水鱼类,有“水中活化石”之称[1]。它具有低脂肪、低能量、高蛋白和多不饱和脂肪酸含量丰富的特点,味道鲜美,经济价值较高[2]。近年来,随 着鲟鱼人工繁育及养殖技术的不断发展与推广,我国已成为鲟鱼养殖的世界第一大国[3]。但新 鲜鱼肉因营养丰富、水分含量高 等特点而极易腐败。Gram等[4]研究发现,在贮藏过程中逐 渐占据优势地位并产生腐败代谢产物的特定腐败菌(specific spoilage organism,SSO)是促使鱼肉腐败的最重要原因之一。由于冷藏鲜鱼货架期短,容易成为食品安全隐患,因此确定鱼肉在贮藏中的SSO并建立其生长预测模型来预测产品 货架期,是预防鱼肉腐败变质的关键手 段之一。
目前微 生物预测模 型已广泛应用于食 品行业当中,其中修正的Gompertz方程、Baranyi方程及Logistic方程是应用较为广泛的一 级模型;二级 模型中,平方根方程及Arrhenius方程使用最为普遍,其中温度是二级模型研究中考虑最多的因素[5]。根据现有文献报道,虽然针对假单胞菌生长预测模型研究较多,但多以液体培养基为培养介质[6-7]或选择性培养基计数[8-11]获得实验数据,虽然操作简便,但没有考虑到食品基质间的组织复杂性和差异性等因素。当然,每种模型都有不同的适用对象和范围,因此需要根据产品特点和相应腐败现象,选择合适的数学模型进行评价,才能保证所构建的模型具有实用价值。
目前针对鲟鱼SSO的生长预测模型和货架期模型的研究较少,本研究以鲟鱼有氧冰藏确定的SSO—荧光假单胞菌(Pseudomonas fluorescens)为实验菌株,将SSO反接于无菌的食品基质中以有效控制微生物初始菌数、保证所建的模型的稳定性、有效模拟实际微生物生长环境,利用修正的Gompertz模型对SSO在有氧包装的无菌鲟鱼鱼片中的生长情况进行拟合,同时就平方根方程与Arrh enius方程描述温度对特定腐败菌生长动力学参数的影响进行了比较。在此基础上,建立了0~20 ℃范围内的特定腐败菌生长预测模型及鲟鱼货架期预测模型,并对模型的可靠性进行了评价,为快速预测有氧贮藏鲟鱼的货架期提供一定的参考。
1 材料与方法
1.1 材料与试剂
鲜活鲟鱼(质量1~1.5 kg,体长40~50 cm)购自北京回龙观城北水产 市场;荧光假单胞菌分离于货架期终点的有氧冰藏鲟鱼鱼肉中,并由菌相和腐败能力分析确定为有氧贮藏鲟鱼的特定腐败菌;营养肉汤培养基、假单胞菌分离培养基 青岛海博生物技术有限公司。
1.2 仪器与设备
LSB35L-I型立式压力灭菌器 江阴滨江医疗设备有限公司;KDY-9820型凯氏定氮仪 北京通润机电技术公司;Satroris PB-10型pH计 赛多利斯科学仪器(北京)有限公司;LRH-250型生化培养箱 上海一恒科技有限公司。
1.3 方法
1.3.1 灭菌鲟鱼片 的制备
参照Macé等[11]的方法并适当调整:将购买的鲜活鲟鱼敲击头部致死后,立刻用50 g/L Na2CO3溶液清洗去除 表面黏液,去除头、尾、内脏。在无菌环 境下再依次用50 g/L Na2CO3溶液、2%福尔马林溶液清洗,无菌条件下切成鱼片(每片约30 g),用无菌水充分洗净后沥干。经培养计数 ,灭菌鱼片的细菌总数小于2(lg(CFU/g))。
1.3.2 菌悬液的制备
将从有氧贮藏鲟鱼腐败终点分离得到、甘油管保藏的荧光假单胞菌于营养肉汤培养基中活化2次,再以2%接种量接种于营养肉汤培养基中,30 ℃培养约12 h,使菌悬液浓度达到8 (lg(CFU/mL)),稀释至5 (lg(CFU/mL))后用于鱼片接种。
1.3.3 接种与贮藏
参照李学英等[12]的方法并作适当调整取:将制备好的灭菌鱼片浸于5 (lg(CFU/mL))菌液中,1 5 s后涝出沥干,经测定鱼肉初始接种量为3~4 (lg(CFU/g)),将接种后的鱼块无菌托盘包装,实验设空白对照, 分别置于0、4、8、10、15、20 ℃及波动温度条件下贮藏(参考SC/T 2009-1999《水产品加工质量管理规范》[13]设计:20 ℃,6 h(加工);0 ℃,2 d(运输销售);20 ℃,2 h(购买回家);4 ℃,贮藏(家庭贮藏))。
1.3.4 指标测定
1.3.4.1 感官评价
感官评价采用质量指数法(quality index method,QIM)。参照朱志伟等[14]的方法并适当调整:参照评定人员由经过专门培训的6 名人员组成。随机抽取不同贮藏期的鱼肉样品,对鱼肉的颜色、光泽度、通透性、气味、表面黏液和质地进行评价。 QIM中每个参数的分值范围根据贮藏期的变化特征在0~3之间,其中0 代表最佳的品质,分数越高质量越差。每个参数分值相加,形成QI值,用以代表鱼肉品质。
1.3.4.2 菌落计数
参照GB/T 4789.2-2010《食品卫生微生物学检验:菌落总数测定》[15]方法,采用假单胞分离培养基对假单胞菌进行计数。
1.3.4.3 pH测定
采用GB/ T 5009.45-2003《水产品卫生标准的分析方法》[16]中的酸度计法测定。
1.3.4.4 挥发性盐基氮(total volatile base nitrogen,TVBN)含量测定
采用GB/T 5009.44-2003《肉与肉制品卫生标准的分析方法》[17]中半微量定氮法测定。
1.3.5 荧光假单胞菌生长预测模型的建立
在0、4、10、15、20 ℃获得的荧光假单胞菌的生长数据,用修正的Gompertz模型拟合不同温度条件下荧光假单胞菌的生长动态。修正的Gompertz模型如式(1)[18-19]:
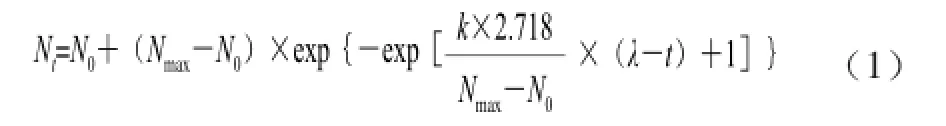
式(1)中:Nt为t时刻微生物的对数值(lg(CFU/g));N0和Nmax分别为Nt的初始值、最大值(lg(CFU/g));λ为恒温条件下迟滞期/h;k为最大比生长速率/h-1。
Bělehrádek平方根方程[20]、Arrhenius方程[21]广泛用于描述温度对荧光假单胞菌的最大比生长速率k和延滞期λ的影响,其表达如式(2)、(3):

式(2)中:T为摄氏温度/℃;Tmin为微生物没有代谢活动时的理论最小温度/℃;bk、bλ为方程常数。
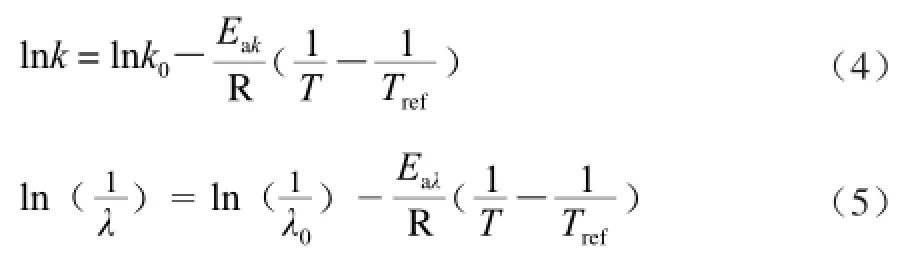
式(3)~(5)中:T为绝对温度/K;Tref为基准温度(273K);k0和λ0分别为Tref时的最大比生长速率/h-1和延滞时间/h;Eak、Eaλ分别是k、λ的活化能/(kJ/mol);R为通用的气体常数/(J/(mol·K))。
1.3.6 生长预测模型可靠性评价
评价预测模型可靠性的最有效的手段之一是将预测值与真实检测数据进行比较。本研究采用准确度(Af)、偏差度(Bf)及残差分析来评价建立的生长预测模型的可靠性。同时参考实际流通条件,以8 ℃和波动温度(同1.3.3节)条件下贮藏鲟鱼实验得到的荧光假单胞菌生长实测值与模型预测值进行比较,验证生长预测模型的可靠性。其中Af、Bf的表达式[22]如下:
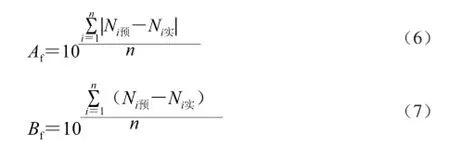
式中:n为实验次数;Ni预为第i次实验预测值;Ni实为第i次实验实测值。
1.3.7 鲟鱼货架 期(shelf life,SL)预测及评价
0~20 ℃的贮藏温度范围内,在建立的荧光假单胞菌生长预测模型的基础上,利用鲟鱼中荧光假单胞菌从初始菌数增殖到感官拒绝点时的最小腐败菌数的时间来表示有氧贮藏鲟鱼的货架期。将在8 ℃和波动温度条件下有氧贮藏的鲟鱼货架期实测值与模型预测值进行比较,根据相对误差的评价货架期预测的可靠性。
1.4 数据分析
所有实验重复测定2 次,数据统计分析采用SPSS 17.0和ANOVA方差分析处理,结果以“平均值±标准误差”表示。
2 结果与分析
2.1 荧光假单胞菌生长预测模型的建 立与可靠性评价
2.1.1 不同贮藏温度条件下荧光假单胞菌的生长预测模型的建立
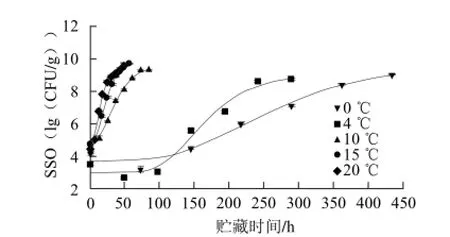
图1 鲟鱼在不同温度条件下的荧光假单胞菌生长曲线Fig.1 Grow th curves of Pseudo monas fl uorescens in sturgeon stored at different temperatures
由表1可知,利用修正的Gompertz方程拟合的R2均大于0.97,拟合度高,模型均为极显著(P<0.000 1),说明该一级模型能够很好地描述荧光假单胞菌的在不同温度条件下的生长曲线,许振伟等[23]对鲤鱼、罗非鱼等研究中均有类似结论。同时,初始菌数值集中在3~4 lg(CFU/g),符合实验预期;稳定期的最大菌数对数9~10 (lg(CFU/g)),平均值为9.55(lg(CFU/g)),受温度影响不大;随着温度的升高,荧光假单胞菌的最大比生长速率k从0℃时的0.02/h增加到20℃的0.24/h;而生长延滞期λ则随温度的升高而减小,0℃时的延滞期最长,为118.93 h,20 ℃时缩短为1.86 h,说明在0~20 ℃范围内,贮藏温度对荧光假单胞菌的k、λ等影响较大。因此贮藏温度常被认为是肉品腐败中最重要的影响因素[24],在SSO二级模型研究中也考虑较多。

表1 不同温度条件下的荧光假单胞菌的生长动力学参数Table1 Kinetic parameters of Pseudomonas fluoresceennss growth at different temperatuurreess
2.1.2 温度对荧光假单胞菌生长动力学参数的影响
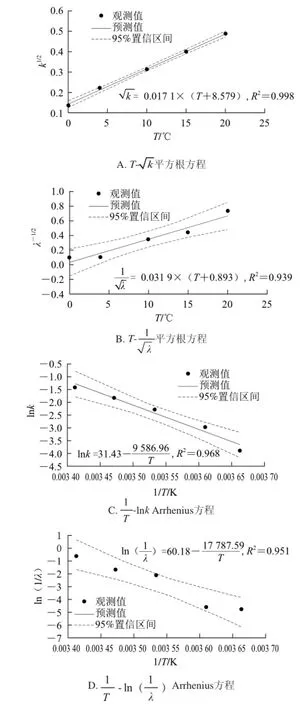
图2 温度对荧光假单胞菌的最大比生长速率(k)、延滞期(λ)的影响Fig.2 Effect of temperature on maximum specific growth rate (k) and lag phase (λ) of Pseudomonas fl uorescens
分别利用平方根方程和Arrhenius方程描述温度T与最大比生长速率k、延滞期λ的关系,从图2可以看出:实际观测值都在95%预测置信区间之内,同时平方根方程和Arrhenius方程分别对k、λ的拟合度均大于0.93,表现出良好的线性相关性。假单胞菌在青鱼、多宝鱼等生长数据均得到类似结论[8,25];平方根方程和Arrhenius方程对T与k的关系的拟合效果均好于对T与λ的关系,这可能是由于延滞期受计数时间、条件的波动和微生物物种的差异等影响较大,从而导致延滞期的预测重复性较最大比生长速率差,预测难度也更大[7]。
2.1.3 荧光假单胞菌生长预测模型的建立与可靠性评价
将2.1.2节中的方程A、B代入修正的Gompertz方程,可以得到基于平方根方程的荧光假单胞菌在0~20 ℃条件下的生长预测模型Ⅰ,表达如下:
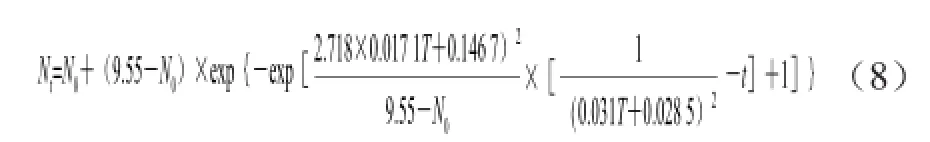
同理,将2.1.2节中的方程C、D代入修正的Gompertz方程,可以得到基于Arrhenius方程的荧光假单胞菌在0~20 ℃条件下的生长预测模型Ⅱ,表达如下:
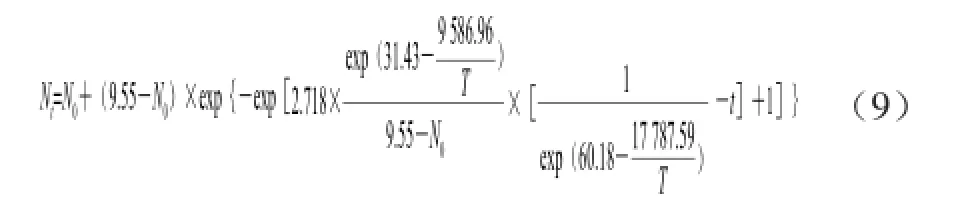

表2 8 ℃、波动温度条件下模型预测准确度(Af)和偏差度(Bf)Table2 Comparison of Afand Bffrom different models under isothermal (8 ℃) and non-isothermal conditions
冷链鲜鱼的温度一般保持在0~8 ℃[26],但在实际加工与流通过程也可能发生冷链中断等情况而造成贮藏温度波动。为使建立的模型更具实用价值,选取在8 ℃、波动温度条件下荧光假单胞菌的生长情况对预测模型进行验证。利用预测值和观察值的直观对比图可以揭示偏差,残差值越接近0,模型越可靠。根据荧光假单胞菌的菌数对数值的残差分析:基于方程(8)得到的8 ℃、波动温度的残差值均在在±0.1以内,没有离群值,观测值较为可靠。但方程(9)得到的8 ℃条件下的残差分布在-0.17~0.1,波动温度为-0.15~0.24,残差分布相对较散。
为进一步对微生物生长预测模型验证,Ross[22]引入偏差因子衡量预测值和观测值之间的平均偏差,利用准确因子评估所建立模型的准确度,其中Af、Bf为1.0表示模型拟合效果最理想。由表2可知,在8℃、波动温度条件下,方程(8)得出的Bf分别为0.97、1.02,Bf平均值为1.00,说明生长预测模型Ⅰ的预测值与实测值基本一致(Bf=1);而方程(9)得出的Bf则为0.94和1.08,Bf平均值为1.01,生长预测模型Ⅱ预测值超出实测值1%(Bf>1),可认为这类模型是安全的(faildangerous)[22]。方程(8)、方程(9)的Af分别为1.14~1.17、1.21~1.31,则生长预测模型Ⅰ的预测误差可能在14%~17%,生长预测模型Ⅱ的预测误差可能在21%~31%,可见基于平方根方程的生长预测模型Ⅰ的预测效果更好。Koutsoumanis等[9]用平方根方程建立了在变温下金头鲷中假单胞菌生长预测模型,预测效果与本研究类似,其中Bf均值为1.04,Af为1.11~1.17,可能的预测误差为11%~17%等;而Bruckner等[10]基于Arrhenius方程的猪肉中假单胞菌生长预测模型的Bf均值为0.97,Af为1.05~1.24,可能的预测误差为5%~24%等,结果较本研究略好。这可能与不同假单胞菌菌种的腐败能力及其作用的食品基质等差异有关。
2.2 0~20 ℃鲟鱼贮藏货架期模型的建立与可靠性评价
2.2.1 特定腐败菌最小腐败值的确定
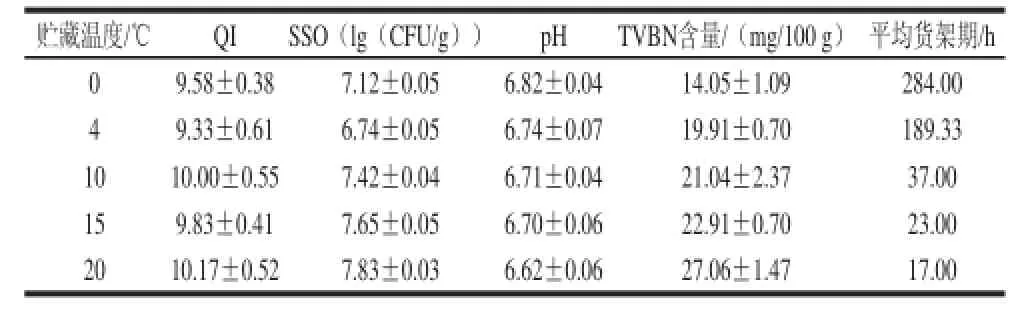
表3 不同贮藏温度条件下感官拒绝点的各指标测定Table3 Physiochemical properties of surgeon stored at different temperatures at the end of shelf life
表3表明,经感官评价得出有氧包装鲟鱼片在0、4、10、15 ℃和20 ℃条件下分别在284.00、189.33、37.00、23.00和17 h达到感官拒绝点,即货架期终点。同时当达到感官拒绝点时,不同温度条件下QI值集中在9~10,pH值约为6.60~6.80,菌数平均对数值为(7.35±0.04)(lg(CFU/g)),TVBN平均值为(20.99±1.27)mg/100 g,达到GB 2733-2005《鲜、冻动物性水产品卫生标准》[27]对淡水鱼的20 mg/100 g卫生限值,说明当菌数对数值超过上述的范围,鱼肉可能腐败,因此,确定荧光假单胞菌菌数的最小腐败平均值为7.35(lg(CFU/g))。国际食品微生物规格委员会规定:消费者对食品中微生物可接受限值为7.00(lg(CFU/g))[28];Bruckner等[10]研究在有氧包装猪肉、禽肉中SSO(假单胞菌)生长情况时,也得到相似的结果,SSO的最小腐败值为7.50(lg(CFU/g)),说明本实验确定的SSO的菌数最小腐败值是可接受的。
2.2.2 货架期预测模型的建立与可靠性评价
已确定的SSO菌数最小腐败值,结合2.1.2节中的方程A、B,由修正的Gompertz方程可以出鲟鱼在0~20 ℃的货架期预测模型Ⅰ,其表达如下:

同理,结合2.1.2节中的方程C、D可以推导出鲟鱼在0~20 ℃的货架期预测模型Ⅱ:
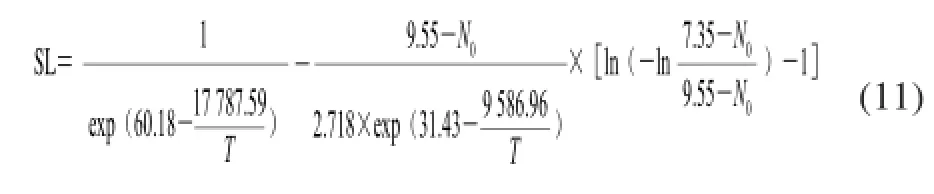
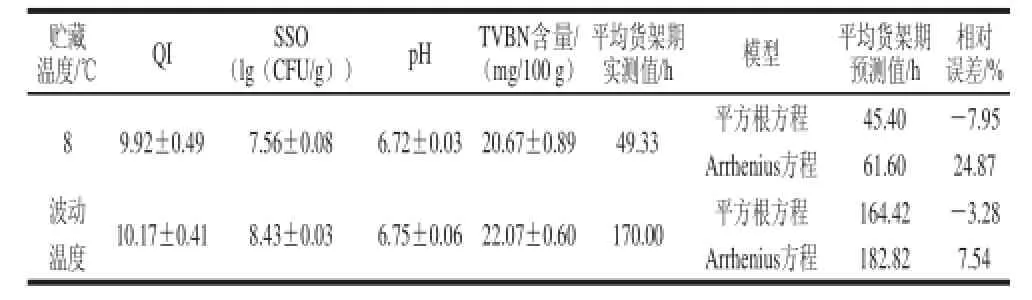
表4 8 ℃、波动温度条件下对货架期预测模型验证Table4 Validation of shelf life prediction models under isothermal (8 ℃) and non-isothermal conditions
根据实际的冷链流通情况,在8 ℃、波动温度条件下对货架期预测模型进行验证。由表4可知:当达到感官拒绝点时,8 ℃和波动温度条件下的菌数对数值分别为(7.56±0.08)(lg(CFU/g))、(8.43±0.03)(lg(CFU/g)),大于荧光假单胞菌菌数的最小腐败值,由于不可能做到对样品实时监测,波动温度条件下的4 ℃贮藏阶段只能每12 h监测一次,这可能是造成误差的原因,但QI、pH值和TVBN值均处于确定的最小腐败水平范围内,因此表4数据仍具有参考价值。与建立的鲟鱼货架期预测模型得到的预测值相比较,方程(10)对8 ℃、波动温度的预测相对误差分别为-7.95%和-3.28%,均小于10%,预测效果良好;而方程(11)的预测相对误差则分别为24.87%和7.54%,对8 ℃条件下的货架期预测偏差较大;可见方程(10)对货架期的预测效果更好。但同一模型在类似的应用(相同的SSO及包装形式等)中,结果仍存在一定的差异。在Gompertz、平方根方程基础上,Koutsoumanis等[9]建立的金头鲷、碎肉货架期预测模型的预测相对误差为5.80%、13.10%;宋志强等[8]货架期预测相对误差则为5.74%~20.80%;Bruckner等[10]基于Gompertz、Arrhenius方程对猪肉、禽肉货架期预测相对误差则为-0.60%~13.30%、-0.50%~26.20%。这可能与研究对象差异、数据采集点的方式和采集数量及确定感官拒绝点的主观差异等有关。
3 结 论
修正的Gompertz模型能够很好地拟合0、4、10、15 ℃和20 ℃条件下SSO(荧光假单胞菌)在有氧贮藏鲟鱼片中生长情况。在此基础上,基于平方根方程的温度模型对0~20 ℃范围内的有氧贮藏鲟鱼片的SSO生长动态和相应的鲟鱼货架期的预测误差更小,预测效果更好。
[1] 高露姣, 夏永涛, 黄艳青, 等. 俄罗斯鲟鱼卵与西伯利亚鲟鱼卵的营养成分比较[J]. 海洋渔业, 2012, 34(1): 57-63.
[2] 庞景贵, 刘丽杰, 陈力. 世界鲟鱼类资源及其养殖前景[J]. 淡水渔业, 2002, 32(1): 53-55.
[3] 孙大江, 曲秋芝, 张颖, 等. 中国的鲟鱼养殖[J]. 水产学杂志, 2011, 24(4): 67-70.
[4] GRAM L, HUSS H H. Microbiological spoilage of fish and fish products[J]. International Journal of Food Microbiology, 1996, 33(1): 121-137.
[5] 李琳, 潘子强. 水产品特定腐败菌的确定及生长模型建立研究进展[J].食品研究与开发, 2011, 32(6): 152-156.
[6] PIN C, SUTHERLAND J P, BARANYI J. Validating predictive models of food spoilage organisms[J]. Journal of Applied Microbiology, 1999, 87(4): 491-499.
[7] 傅鹏, 李平兰, 周康, 等. 冷却肉中假单胞菌温度预测模型的建立与验证[J]. 农业工程学报, 2008, 24(4): 229-234.
[8] 宋志强, 刘超群, 侯温甫. 草鱼鱼整片品质变化研究及货架期预测[J].食品工业, 2013, 34(9): 123-127.
[9] KOUSTSOUMANIS K. Predictive modeling of the shelf life of fish under nonisothermal conditions[J]. Applied and Environmental Microbiology, 2001, 67(4): 1821-1829.
[10] BRUCKNER S, ALBRECHT A, PETERSEN B, et al. A predictive shelf life model as a tool for the improvement of quality management in pork and poultry chains[J]. Food Control, 2013, 29(2): 451-460.
[11] MACÉ S, Joffraud J J, Cardinal M, et al. Evaluation of the spoilage potential of bacteria isolated from spoiled raw salmon (Salmo salar) fillets stored under modified atmosphere packaging[J]. International Journal of Food Microbiology, 2013, 160(3): 227-238.
[12] 李学英, 杨宪时, 郭全友, 等. 大黄鱼腐败菌腐败能力的初步分析[J].食品工业科技, 2009, 30(6): 316-319.
[13] 国家水产品质量监督检验中心. SC/T 3009—1999 水产品加工质量管理规范[S]. 北京: 中国标准出版社, 2010.
[14] 朱志伟, 李汴生, 阮征, 等. 脆肉鲩鱼片冷藏货架期的QIM及理化方法评价的比较研究[J]. 水产科技, 2010, 27(4):11-16.
[15] 国家质量技术监督局. GB 4789.2-2010 食品微生物学检验: 菌落总数测定[S]. 北京: 中国标准出版社, 1999.
[16] 上海市食品卫生监督检验所, 江苏省卫生防疫站, 杭州市卫生防疫站, 等. GB/T 5009.44—2003 水产品卫生分析标准方法[S]. 北京: 中国标准出版社, 2004.
[17] 上海市食品卫生监督检验所. GB/T 5009.44—2003 肉与肉制品卫生标准分析方法[S]. 北京: 中国标准出版社, 2004.
[18] ZWIETERING M, JONGENBURGER I, ROMBOUTS F, et al. Modeling of the bacterial growth curve[J]. Applied and Environmental Microbiology, 1990, 6(6): 1875-1881.
[19] HUANG L. A new mechanistic growth model for simultaneous determination of lag phase duration and exponential growth rate and a new Bĕlehdrádek-type model for evaluating the effect of temperature on growth rate[J]. Food Microbiology, 2011, 28(4): 770-776.
[20] DAVEY K. A predictive model for combined temperature and water activity on microbial growth during the growth phase[J]. Journal of Applied Microbiology, 1989, 67(5): 483-488.
[21] RATKOWSKY D, OLLEY J, MCMEEKIN T, et al. Relationship between temperature and growth rate of bacterial cultures[J]. Journal of Bacteriology, 1982, 149(1): 1-5.
[22] ROSS T. Indices for performance evaluation of predictive models in food microbiology[J]. Journal of Applied Microbiology, 1996, 81(5): 501-508.
[23] 许振伟, 李学英, 杨宪时, 等. 冷藏鲤鱼和罗非鱼优势腐败菌腐败能力分析[J]. 食品科学, 2012, 33(4): 243-246.
[24] DOULGERAKI A I, ERCOLINI D, VILLANI F, et al. Spoilage microbiota associated to the storage of raw meat in different conditions[J]. International Journal of Food Microbiology, 2012, 157(2): 130-141.
[25] 张璐, 侯红漫, 伦成成. 多宝鱼优势腐败菌生长动态模型和货架期预测[J]. 食品科技, 2010, 35(7): 158-162.
[26] 曲敏. 鲜鱼冷却链物流技术与货架期预测[J]. 现代农业科技, 2011(21): 334-336.
[27] 辽宁省食品卫生监督检验所, 上海市卫生监督所, 大连市卫生防疫站, 等. GB 2733—2005 鲜、冻动物性水产品卫生标准[S]. 北京: 中国标准出版社, 2005.
[28] NOORDHUIZEN J, WELPELO H. Sustainable improvement of animal health care by systematic quality risk management according to the HACCP concept[J]. Veterinary Quarterly, 1996, 18(4): 121-126.
Predictive Modeling of Pseudomonas fl uorescens Growth and Shelf Life Prediction of Stu rgeo n
ZHANG Zhi-chao1, GUI Meng1, PENG Chao-hui2, LI Ping-lan1,*
(1. College of Food Science and Nutritional Engineering, China Agricultural U nive rsity, Beijing 100083, China; 2. Beijing Beis hui Food Co. Ltd., Beijing 100068, China)
The aim of this study was to establish predictive models for the growth of Pseudomonas fl uorescens in sturgeon and its shelf life. Pseudomonas fluorescens, the special spoilage organi sm (SSO) of aerobically stored sturgeon, was inoculated to sterile sturgeon fi llets and stored aerobically at 0, 4, 10, 15 or 20 ℃. The models were developed based on the data of kinetic growth of Pseudomonas fl uorescens and sensory evaluation, pH, total volatile base nitro gen (TVBN) at the end of the shelf life of sturgeon. On the basis of the m odifi ed Gompertz equation, square root equations and Arrhenius equations were used as the secondary models to construct the prediction models of growth and shelf life for Pseudom onas fl uorescens. The results showed that the average logarithmic val ue of Pseudomonas fl uorescens was (7.35 ± 0.05) lg (CFU/g) at the end of shelf life. Meanwhile, the models were validated under isothermal (8 ℃) and non-isothermal conditions. The residual errors, accuracy factors (Af), bias factors (Bf) and relative errors of shelf lives from the models based on square root equations we re -0.09–0.10, 1.14 and 1.1 7, 0.97 and 1.02, and -7.95% and -3.28%, respectively. In contrast, the residual errors, Af, Bf, and relative errors of shelf lives from the models based on Arrhenius equation were -0.17–0.24, 1.21 and 1.31, 0.94 and 1.08, and 24.87% and 7.54%, re spectively. In conclusi on, the square root equatio n models were more ef fective for predi cting the growth of Pseudomonas fl uorescens and the shelf lives of sturgeon stored aerobically at 0–20 ℃.
sturgeo n; Pseudomonas fl uorescens; tem perature; prediction mo del; shelf life
S983
A
1002-6630(2014)10-0278-06
10.7506/spkx1002-6630-201410052
2014-01-04
北京市鲟鱼、鲑鳟鱼创新团队项目(SCGWZJ20131105-2)
章志超(1989—),男,硕士研究生,研究方向 为食品微生物学。E-mail:zhgio2008@126.com
*通信作者:李平兰(1964—),女,教授,博士,研究方向为食品微生物学。E-mail:lipinglan@cau.edu.cn

