基于多级计分题目的分步功能差异检验
李美娟,刘红云
(1.北京教育科学研究院,北京 100191;2.北京师范大学心理学院,北京 100875)
0 引言
从20世纪60年代起,美国教育界就开始关注性别与种族在测验结果上的差异,即测验公平的问题.测验的公平性是测验研发者、使用者,乃至整个社会所普遍关注的一个非常重要而又异常复杂的问题.对于中国这个考试大国来讲,为了提高试题质量,对于一些高考、公务员等考试进行题目的公平性检验是十分必要的.美国的教育研究学会(AERA)、心理学学会(APA)、教育测量年会(NCME)认为测验的公平必须满足4个条件:(i)项目没有偏差;(ii)所有的考生都有平等的机会证实自己对于测验内容掌握的熟练性程度;(iii)所有的考生都有平等的机会学习测验内容(除了就业、认证或者入学考试);(iv)不同类别考生的分数分布是相同的[1].中国教育学会教育测量与统计分会认为测验公平性是指如果一个测验对来自不同团体而具有相同能力或熟练程度的个体所测得的特性相同,则说明该测验具有公平性,如果测得的特性不同,则说明该测验不公平而具有偏差[2].即公平性检查的目的是找出是否存在测验范围之外引起组间差异的因素.
项目偏差这个概念是美国在20世纪60年代提出的,主要用于对跨文化团体、性别、种族差异的研究.一直以来,对于项目偏差的研究,项目功能差异(DIF,differential item functioning)一直发挥着非常重要的作用,DIF是项目偏差的充分而非必要条件.相对于项目偏差,DIF是一个有关统计分析的术语,表示不同团体相同能力水平的被试对于相同测验题目的通过率却不同,引起DIF的原因是2组被试在与测验所测的能力无关的知识或经验上存在差异[3-5].目前大多数检测DIF的方法都集中在2级计分题目上,其中包括(i)非参数方法:MH,SIBTEST,LRDIF,STND等;(ii)参数方法:基于IRT的Lord卡方检验法,Raju面积测量法和似然比率法(IRT和LRDIF);而对于多级计分题目DIF的检测方法多来源于2级计分题目检测方法的拓展,目前也有许多关于多级计分题目DIF检测的方法,其中包括标准化均值差异法、Mantel的卡方检验、广义 Mantel-Haenszel法、多级SIBTEST法、逻辑斯蒂克判别函数分析法、累积发生比方法等.但是,这些传统的多级计分题目检测DIF的方法只能提供项目水平上的DIF指标,不能测量题目在哪个分数水平上存在DIF,进而也不能进一步解释DIF的产生原因.
纵观国外对于DIF的研究,大多数研究者集中在其方法的探讨上,有少数研究涉及到DIF检测的影响因素,如样本量、维度,以及模型的参数等方面.而国内对DIF的研究也比较早,主要是对DIF相关概念以及检测方法的研究.之后也有不少研究者使用实际数据对DIF检测方法进行应用,并对几种方法进行比较,还有一些研究者将DIF的检测直接应用到心理测验中,对心理测验的公平性进行初步探讨.但是很少有研究对DIF的解释进行深入分析,或者对产生DIF的原因进行挖掘,从而使测量在心理学的实际应用中变得更有意义.近年来,对多级计分项目的DIF的研究有进一步细化和深入的趋势,本研究的目的在于回顾DIF研究方法这一领域的新进展及应用,介绍一种新的检测DIF的方法——分步功能差异(DSF)检验法,同时结合一个实际测验,简要介绍这一方法的具体应用.本研究的目的在于为研究者进一步探讨产生DIF的原因提供更充分的依据和途径.
1 分步功能差异(DSF)的相关概念
1.1 分步函数的定义
分步功能差异(DSF)可以检测多级计分题目的不同分数水平上是否存在DIF,即通过分步函数的特征(基本参数)得到特定能力的被试在各个分数水平上正确做答的概率[6].其分步函数根据IRT模型的不同具有不同的形式.基于不同形式的分步功能特征的含义是不同的,最常用的是等级反应模型(GRM)下的累积形式和分部计分模型(PCM)下的连接形式的分步功能差异.
分步函数主要是在多级计分题目上,个体从低分数水平跨越到高分数水平的概率,对于一个有r个分数水平的多级计分题目,则有J=r-1个分步水平.例如,一个4级计分题目,分数水平定为0,1,2,3,r=4,分步水平 J=3,结果用符号 Y 表示.其累积形式的分步函数是:(i)被试从分数水平0到分数水平1或者高于1的概率,即Y≥1概率;(ii)被试从分数水平1到分数水平2或者高于2的概率,即Y≥2概率;(iii)被试从分数水平2到分数水平为3的概率,即Y=3概率.而其连接形式的分步函数是:(i)被试从分数水平0到分数水平1的概率,即Y=1概率.(ii)被试从分数水平1到分数水平2的概率,即Y=2概率.(iii)被试从分数水平2到分数水平3的概率,即Y=3概率.
1.2 分步函数的参数
每个分步水平均使用2参数Logistic回归模型进行参数估计[7]:

其中bj为j分步水平的难度系数,且每个分步水平的难度系数是不同的;a为分步水平的区分度系数,且每个分步水平的区分度系数是相同的;θ为被试的能力水平;D为1.7.G=0为目标组,G=1为参照组.a描述了每个分步水平能够区分高低能力被试的程度,bj描述了通过该分步水平的概率为0.5的特定被试的能力水平.在GRM模型中,假设bj随着分步水平的提高而增加,而在PCM模型中,则没有这样的假设.ωj=0表示不存在DSF,ωj>0表示参照组占优势,ωj<0表示目标组占优势.
1.3 一致性DSF和非一致性DSF的概念
在DSF的分析中,一致性DSF和非一致性DSF是基于j个分步水平的DSF分析.一致性DSF指j个分步水平的DSF均相同,而非一致性DSF是指j个分步水平的DSF不完全相同[8].由此可见,虽然DSF和2级计分题目DIF的研究较相似,但是对于非一致性DIF和DSF,组间a参数差异的不同是区分两者最重要的因素.在2级计分题目中,a参数的不同表示非一致性DIF的存在,而非一致性DSF表示在不同的分步水平上2组DIF方向不一致或DIF大小程度不一致,如DSF分析结果在第1个分步水平上有利于男生组,在第2个分步水平上有利于女生组,以上属于非一致性DSF的一种情况.
非一致性DSF的检测方法与2级计分的非一致性DIF检验方法是相同的,但是相关研究文献中还没有真正应用过,所以应用的价值还有待进一步证实.
2 DSF的估计
已有研究关于DSF的估计方法主要有参数和非参数2类方法,其中参数法主要有IRT方法,而非参数法主要有odds比率法和Logistic回归法.这些方法曾是检测2级计分DIF的方法,所以在应用时要注意:(i)必须将所研究题目的等级水平转化为j个分步水平,(ii)必须对每个分步水平独立分析.
2.1 分步水平的建构方法
虽然从理论上讲构建分步水平的方法有多种,但主要的是以广义分部计分模型[9](GPCM)为基础的连接方法(AC-LOR)和以等级计分模型[10](GRM)为基础的累积方法(CU-LOR),这2种方法对DSF的定义如前所述,但是2种概念下DSF的结果和解释是否相同也是DIF研究者们需要深入考察的一个内容.对以这2种模型为基础的DSF发生比方法进行了统计特征的模拟研究比较,结果发现累积方法下的DSF结果更稳定[7],精确性更高.另外,将2种方法应用于实际数据时[11],当不存在DSF或者DSF很小时,两者结果一致.但是第1种方法缺乏独立性,一个水平存在较大的DSF,将伴随着高水平反方向的较大DSF.当存在较大的DSF时,使用第2种方法更容易获得显著的结果,而且这种方法标准误更小,稳定性和检验力更强.研究还发现,当仅有一个分数水平上存在DSF时,第1种方法的精确性更强,解释更加合理.
2.2 参数估计方法
IRT检测DSF的基础是比较参照组和目标组在多级计分题目的每个分步水平上的差异[8],表示为Δ(bj)=bjF-bjR.如果 Δ(bj)=0,则不存在 DSF.若Δ(bj)>0,则表示参照组占优势.反之,目标组占优势.Δ(bj)为j分步水平上参照组和目标组的有符号面积测度[12],这与 Raju对2级计分题目DIF的面积测量法是相同的.因此,DSF的效应大小的衡量标准与Raju的面积测量法的衡量标准是相同的.
常用的检验标准是:若︱Δ(bj)︱<0.25,则表示较小的DSF值.︱Δ(bj)︱<0.50,则表示中等的DSF值.如果︱Δ(bj)︱>0.50,则表示较大的DSF值.检验IRT模型下不存在DSF的虚无假设的方法有2种,其中一种是将Δ(bj)除以标准误,并且假设其是标准正态分布的.另外一种方法是似然比检验法,即将紧缩模型(2组项目参数固定)和扩展模型(自由估计2组分步函数参数)的似然值进行比较.
2.3 非参数方法
与检验DSF的参数方法比较,在实际应用中非参数方法更受欢迎,因为其不受样本量、数据与模型拟合程度的影响,而且易操作.
2.3.1 发生比方法(odds ratio) 发生比方法(odds ratio)主要是比较参照组和目标组成功通过j分步水平的发生比,该发生比的自然对数就是λ值,即不同能力水平被试的λ值[13].λ的算法为

其中Ajk为k能力水平的参照组成功通过j分步水平的人数;Bjk为k能力水平的参照组未成功通过j分步水平的人数;Cjk为k能力水平的目标组成功通过j分步水平的人数;Djk为k能力水平的参照组未成功通过j分步水平的人数;若λj=0,则表示在j分步水平上不存在DSF;若λj>0,则表示在j分步水平上,题目得分会有利于参照组;若λj<0,则表示j分步水平上,题目得分会有利于目标组.
发生比(odds ratio)方法可以检验DSF的显著性,检验方法为
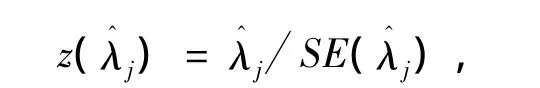
其中 SE(λ^j)的算法如下:

另外,上述方程所检验的统计量服从标准正态分布的[14].
ETS常用的判断标准为:当︱λj︱ <0.43时,则表示存在较小的DSF值;当0.43≤︱λj︱≤0.63时,则表示存在中等的DSF值;当︱λj︱ >0.63时,则表示较大的DSF值.
2.3.2 Logistic回归 估计DSF的另一种非参数方法是Logistic回归[8],模型表述为

其中Y为被试在某个项目上第j步的得分,X为测验总分.G为一个关于组别变量的虚无变量,并且是G=0代表目标组,G=1代表参照组.βj2为j分步水平的DSF效应.其中βj2=0为j分步水平不存在DSF,βj2>0则表示j分步水平上存在DSF,题目得分有利于参照组,βj2<0则表示j分步水平上存在DSF,题目得分有利于目标组.这个方法也可以通过在模型中加入测验分数X和分组变量G的交互作用来考察是否存在非一致性DSF.
显著性检验方法:似然比方法,即将紧缩模型(无βj2G项)和扩展模型(有βj2G项)的似然值进行比较.统计软件提供β的估计值,显著性水平以及模型的(-2×似然值),以便进行适当的似然比检验.该方法划定DSF范围的标准是ΔR2,若ΔR2<0.10,则表示较小的DSF值,若0.10≤ΔR2≤0.20,则表示中等的DSF值.若ΔR2>0.20,则表示较大的DSF 值[15].
2.4 3种估计方法之间的区别和联系
IRT参数估计要求样本量大,数据需与相关分步函数拟合,并且该方法比较耗时,建议使用BILOGMG3、IRTLRDIF[16]和 MULTILOG7.DIFAS程序,均可计算 λj和 z(λj)[17].如果在观测分数与IRT模型拟合的情况下,并且将测验总分认为是能力水平的近似估计时,3种估计方法的结果具有一定的关系,即 Logistic回归(迭代法)和 odds ratio(非迭代法)方法估计的β值和λj是等值的[18],另外,这2个数值与2组难度系数的差异是成比例的,其中比例系数就是区分度值[16].
3 使用DSF的结果检测DIF
3.1 利用DSF效应模式识别DIF产生的原因
R.D.Penfield等[19]根据 DSF产生的轨迹将DSF分为普遍性DSF和非普遍性DSF,普遍性DSF是指所有的分步水平都有DSF效应,说明导致DIF的因素在题目水平上造成影响.而非普遍性DSF是指一些分步水平上存在DSF,说明导致DIF的因素仅仅在一个或者少数几个分步水平上造成影响.根据DSF产生的一致性将分为一致性DSF、会聚性DSF、发散性DSF 3种.一致性DSF是指分步水平DSF值的大小和符号都相同,会聚性DSF是指分步水平的DSF值符号相同,大小却不同,发散性DSF是指分步水平的DSF值符号不同,详见表1.
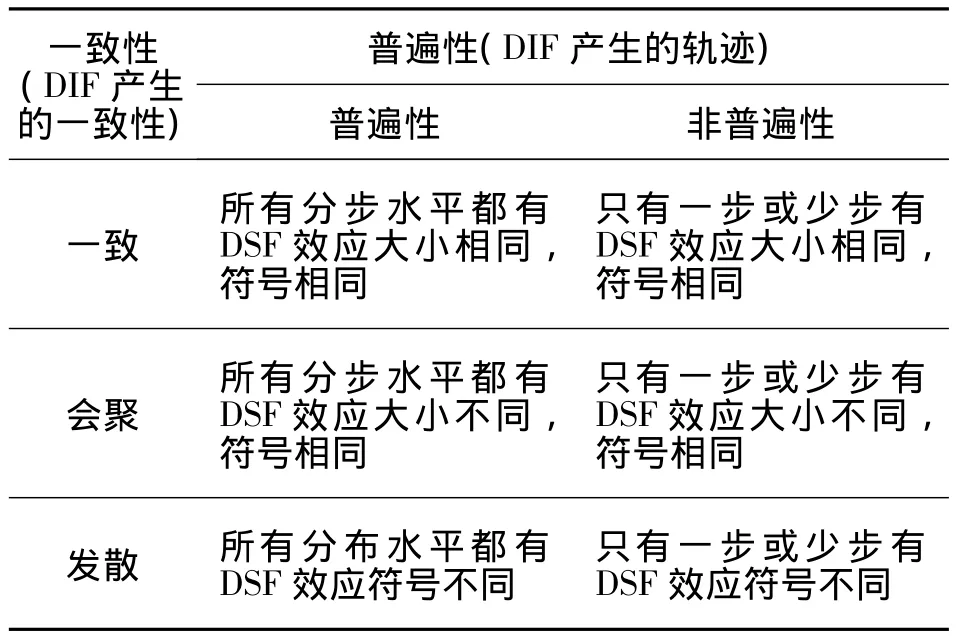
表1 DSF效应模式
一致普遍性DSF对DIF的产生源于题目水平的特征提供了充足的证据,而一致非普遍性DSF说明DIF的产生不一定源于题目水平的特征,而是源于存在DSF效应的分步水平的特征.会聚性DSF说明DIF可能源于题目水平的特征,也可能源于不同分数水平的不同特征.会聚性DSF的解释很有挑战性,尤其在分步水平较多的情况下.发散性DSF给DIF源于不同分步水平的特征提供了充足的证据,而且不同的分步特征使得有利的组别不同.所以DIF研究者的任务就是检测定义分步水平的分数等级的特征,从而识别是一个特征对不同分步水平有影响还是多个特征分别对不同分步水平有影响.
3.2 基于DSF结果检验项目DIF
每个分步水平不存在DSF是题目不存在DIF的充分必要条件.这种方法也就是R.D.Penfield提出的DIF同时性分步水平检测方法(SSL),其源于发生比的DSF估计法[6].SSL基于分步水平,并且在DSF的符号和大小随着分步水平的变化而变化时,具有比其它DIF方法更强的检验力.
上述方法也就是DIF的global检验方法的一种,DIF的global检验则关注无符号DSF,因此它对发散性DSF是敏感的.当分步水平的DSF符号不同、大小不同时,global检验法对DIF的检测是比较敏感的,其中现有的global检验法包括,IRT的似然比方法,多级逻辑斯蒂克回归方法,广义的MH卡方检验法,还有SSL法[7],但是在分步水平的 DSF一致时,net检验法的敏感性更强.DIF的net检验基于所有分步水平有符号DSF的集合,它对发散性DSF是不敏感的.其中DIF的net检验包括Mantel的卡方检验法、多级计分SIBTEST检测法、标准均值差异和其相关方法,以及 Liu-Aresti的累积 common odds ratio估计法.因此,DIF的 net检验对发散性DSF是不敏感的,而 DIF的 global检验对发散性DSF 是敏感的[21].
3.3 DSF和DIF的联合使用
对于如何使DIF和DSF的检测最有效地发挥作用,最重要的是弄清楚两者在多级计分模型中评价测量不变性的优缺点.在关注造成DIF的分数水平时,DIF的检测并没有提供任何的信息.相反,DSF的检测却能提供给项目水平的DIF提供分数水平上的信息.虽然DIF存在这样的缺点,但是有时DIF的检验力可能更强.因为其分析综合了j个分步水平的结果.总之,DIF在非等同测量中可能更敏感,而DSF可以给非等同测量的形式提供更多的信息.
基于DIF和DSF检测的优缺点,建议在虚无假设为不存在DIF的多级计分题目中,测量等同的开始阶段则同时使用DIF的net检验和global检验.前有研究发现:(i)当DSF效应不一致时(除了普遍性DSF),global检验法的检验力更强.(ii)当DSF效应一致时(普遍一致性DSF),net检验法的检验力更强.如果结果接受虚无假设,则说明测量的等同性存在,如果拒绝虚无假设,则说明需要进一步的DSF分析[20].
因此,DSF和DIF检验的联合可以提高敏感性,并且可以给题目提供更多的信息.DSF的检测可以对DIF产生原因和轨迹提供更多的信息.在实际应用中,建议同时进行DIF的net检验和global检验,如果两者中的一种检验结果显著,那么需要继续进行DSF的检测[19],所以建议同时使用3种方法对DIF进行检验,检验力会更强.
4 应用举例
以下是一个对DSF使用以及解释的实证研究.本研究的研究材料是Ralf Schwarzer等编制的一般自我效能感量表[21],其中有10个题目,均为4点计分.被试为美国人和香港人,其中美国被试1 167人,约占48%,香港被试1 152人,约占52%.另外,在此研究中,美国为参照组,香港为目标组.
分别使用发生比方法,Logistic回归法,IRT方法对自我效能感量表的10个题目DSF分析.结果如表2所示.

表2 发生比的DSF数据分析
在表2中,使用DIFAS程序[17]计算各分步水平上的 common log-ratio(λj),λj值的标准误.为了验证如何将DSF的分析与DIF结合在一起,每个题目也均进行了global和net检验,其中DIF的global检验对每个分步水平的DSF进行显著性水平为Bonfereoni-adjusted Typed Ierror rate(0.05/J)的显著性检验,而DIF的net检验使用Liu-Agresti累积 common Log-odds ration(LA),LA值服从正态分布,可通过Z值对其进行显著性检验[22].
在表2中第1列为题目,第2列为分步水平,第3列为λi,第4列为λi的标准误,第5列为显著性水平为Bonfereoni-adjusted typed I error rate(0.05/J)的显著性检验,即DSF的global检验,第6列是根据判断标准判别的DSF效应大小,第7列为DSF模式,第8列为DSF的net检验.
表3中,使用Logistic回归法(SPSS)和IRT方法(Multilog软件)对上述10个题目进行DSF分析,结果发现,Logistic回归法和IRT方法计算的结果与发生比方法的计算结果基本相似,符合上文中的理论假设,另外,也说明该数据和IRT的分步函数是拟合的.
综上所述,本研究将使用发生比方法对研究结果进行解释,在本结果中,8个题目的global检验结果显著,net检验结果也显著.DSF模式完全决定于DSF的大小,而不是DSF效应的显著性水平.研究结果发现,2,7,10题的net DIF检验显著,且DSF属于普遍一致型,由此可以说明造成DIF的原因在于题目本身;2题和7题的λ值为正,表明对于第2和7题讲,相同自我效能感的香港人和美国人,美国人在此题目上会得分更高,而10题相反,香港人得分会更高.9题属于普遍会聚型DSF,说明造成DIF的原因在于不仅在于题目本身,而且在于题目选项的设置,λj值越大,说明选项j的设置出现问题的程度越大,并且λ值为正,则说明在每个选项的设置上美国人得分都比较高,只是差异程度不同.3,4,5,8题的DSF属于非普遍会聚型,与前面一致的是,λj值越大,说明选项j的设置出现问题的程度越大,并且具有中等或者较大程度λ值的选项j的设置标准比较容易出现问题.总之,使用该问卷对美国人和香港人的自我效能感进行测量和比较是很不公平的.

表3 Logistic方法和IRT方法的DSF分析
5 本方法的未来研究趋势以及局限
分步功能差异(DSF)检验法的优点是:(i)测量不变性水平高于DIF的整体测量方法.(ii)DSF方法可以分数水平上(分步水平)分析产生DIF的原因.即如果一个多级计分题目标记有DIF,那么DSF可以分离题目的成分来确定导致DIF的原因给题目内容的审核以及修订提供依据.造成DIF的影响因素是修订或者删除题目的关键[18].(iii)越来越多的研究者对题目认知策略感兴趣[23],这就强调了研究者应在有关认知策略的测量特征上理解组别差异,而DSF可以对多级计分题目检测其认知策略的组别差异.但是,面对一个显著的分步水平DSF值,研究者的任务就是将分步水平的DSF转为特定分数水平的DSF.2种概念下DSF的解释是不同的,由于累积方法的DSF稳定性强,所以其是研究者们常用的一种方法.例如,4级计分题目的第2个分步水平上存在DSF表示2个最低分数水平到2个最高分数水平的过渡对于其中一个组来说要更难.但是,仅DSF是不足以说明哪个高分数水平造成DSF,有可能是第3个分数水平,也有可能是第4个分数水平,也有可能两者都有.
一些研究者提出的策略是,如果一个分步水平上存在DSF(如,第j分步水平)表示在第j个分数水平上存在着组间差异,说明DIF的产生是由于第j个分数水平的特征因素造成的;如果第j和j+1个分步水平均存在着组间差异,说明DIF的产生是由于第j和j+1个分数水平的特征因素造成的.但是通过这种方法计算的结果是有偏的,所以寄予在未来研究中能够发现一种能够对分步水平到分数水平进行准确转化的方法,也希望未来的研究能够更深刻得理解非一致性DSF,并且进一步对检测非一致性DSF的方法进行研究和实践应用.另外,DSF是DIF研究领域的一种新方法,其可以在分数水平上检测DSF,从而对DIF产生的原因深入探讨,但是无论从方法上来讲,还是从实践上来讲,这种方法还不是很成熟,所以期望未来大量的将其应用于心理测验的实证研究,进而为测验公平性提供充足的证据.
[1] American Educational Research Association,American Psychological Association,National Council on Measurement in Education.Standards for educational and psychological testing[M].Washington D C:American Psychological Association,1999.
[2]中国教育学会教育测量与统计分会.测量术语测验公平性[J].中国考试,2003,12(上半月刊):19.
[3]Holland PW,Thayer D T.Differential item performance and the Mantel-Haenszel procedure[C].NJ:Erlbaum,1998:129-145.
[4]Penfield R D,Camilli G.Differential item functioning and item bias[C].New York:Elsevier,2007:125-167.
[5]Zumbo B D.Three generations of DIF analyses:considering where it has been,where it is now,and where it is going [J].Language Assessment Quarterly,2007,4(2):223-233.
[6] Penfield R D.Assessing differential step functioning in polytomous items using a common odds ratio estimator[J].Journal of Educational Measurement,2007,44(3):187-210.
[7]Penfield R D.Three classes of nonparametric differential step functioning effectestimators[J].Applied Psychological Measurement,2008,32(6):480-501.
[8]Penfield R D,Gattamorta K,Childs R A.An NCME instructionalmodule on using differential step functioning to refine the analysis of DIF in polytomous items[J].Educational Measurement:Issues and Practice,2009,28(1):38-49.
[9]Muraki E.A generalized partial credit model:application of an EM algorithm[J].Applied Psychological Measurement,1992,16(2):159-176.
[10]Wim Jvan der Linden,Ronald K Hambleton.Handbook of modern item response theory[M].New York:Springer-Verlag New York Inc,1997:85-100.
[11]Gattamorta K A.A comparison of adjacent categories and cumulative DSF effect estimators[D].Miami:University of Miami,2009.
[12]Cohen A S,Kim SH,Baker F B.Detection of differential item functioning in the graded response model[J].Applied Psychological Measurement,1993,17(4):335-350.
[13]Penfield R D.A nonparametricmethod for assessing differential step functioning in polytomous items[C].San Francisco:CA,2006.
[14] Hauck W W.The large sample variance of the Mantel-Haenszel estimator of a common odds ratio[J].Biometrics,1979,35(4):817-819.
[15]Jodoin M G,Gierl M J.Evaluating type I error and power rates using an effect sizemeasure with the logistic regression procedure for DIF detection [J].Applied Measurement in Education,2001,14(4):329-349.
[16]Thissen D.IRTLRDIF v.2.0 b:software for the computation of the statistics involved in item response theory likelihood-ratio tests for differential item functioning.2001,Unpublished ms.
[17]Penfield R D.Computer program exchange DIFAS:differential item functioning analysis system [J].Applied Psychological Measurement,2005,29(2):150-151.
[18]Alvarez K,Penfield R D.Using differential step functioning(DSF)to refine the analysis of DIF in polytomous items:an illustration[C].Washington D C,2007.
[19]Penfield R D,Alvarez K,Lee O.Using a taxonomy of differential step functioning to improve the interpretation of DIF in polytomous items:an illustration [J].Applied Measurement in Education,2009,22(1):61-78.
[20]Penfield R D.Distinguishing between net and global DIF in polytomous items[J].Journal of Educational Measurement,2010,47(2):129-149.
[21]Schwarzer R,Jerusalem M.Generalized self-efficacy scale[EB/OL].[2014-05-16].www.thefindingsgroup.com.
[22]Penfield R D,Algina J.Applying the Liu-Agrestiestimator of the cumulative common odds ratio to DIF detection in polytomous items[J].Journal of Educational Measurement,2003,40(4):353-370.
[23] Leighton JP,GierlM J.Defining and evaluatingmodels of cognition used in educational measurement to make inferences aboutexaminees’thinking processes[J].Educational Measurement:Issues and Practice,2007,26(2):3-16.
- 江西师范大学学报(自然科学版)的其它文章
- 材料带隙和阴极功函数对有机太阳能电池开路电压的分析

