基于极点展开法无芯片电子标签的识别与传感
胡 伟,邹传云,胥 磊,苏立冬
(西南科技大学 信息工程学院,四川 绵阳 621010)
射频识别技术(RFID)[1]是20世纪80年代发展起来的一种新兴自动识别技术,射频识别技术是一项利用射频信号通过空间耦合,实现无接触信息传递并通过所传递的信息达到识别目的的技术。目前无芯片RFID标签类的识别,大都采用频率内的幅度,相位等之间的变化关系,来对标签结构的识别。但存在许多的限制,观测的方位,激励的入射角度,入射波的极化角度等变化,频率内的数据也会随之发生变化[2-6]。为克服这些限制,C.Baum提出奇点展开法[7-9],在复频域内,散射场的信号可以由极点与相应的留数共同表征,信号的特性由极点与留数确定,极点与散射体结构有关,与其它外部因素无关。留数则与其它的外界因素有关,可以通过留数的变化感知外界的条件因素。文献[10]设计分析一种开槽型的标签结构,本文在此研究的基础上,进一步地利用极点展开的方法与理论,应用极点与留数的特性关系,不仅可以对标签结构的识别,还可感知标签结构其它特征。
1 极点展开法与矩阵束算法的相关理论
1.1 极点展开法的理论
根据C.Baum提出的理论,电磁波激励金属导体时,瞬态响应后期可以近似成一系列的衰减复指数之和,可以将时域信号表示为如下公式所示的形式。
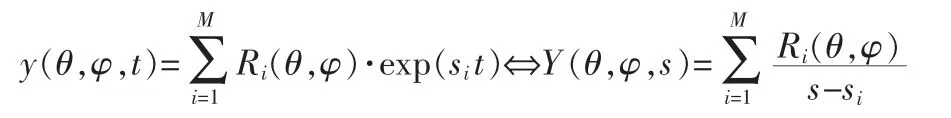
其中,y(t)是观测时域信号;Ri是留数;Si可以表达为 σi+jωi,σi为衰减因子,ωi为谐振频率。
在复频域,信号的特性由极点(或称奇点),留数等参数确定,极点的个数及大小与金属导体的结构有关,与其它的外部因数和激励无关。相应的留数,则与激励的波形,入射波的入射方向,观测的角度等参数有关。通过极点与留数,可以表征信号的衰减因子,谐振频率,幅度,以及相位。由于极点是结构的基本属性,与其它别的因数无关,从而可以通过极点的变化来映射结构的变化,可以通过极点来对导体标签结构的识别,留数感知标签结构的其它物理信息的功能。
1.2 极点的提取
目前,极点提取的办法有prony法,矩阵束算法[5]等数学方法,矩阵束算法,与prony法相比较,具有低方差,高效等特点。其矩阵束法的基本思想是,将得到的数据信息转化成矩阵的形式,并根据数据矩阵间的相互关系求解它们的广义特征值,广义特征值包含了所要求解的信息(信号的极点),因此,求解“衰减指数和”的信号模型的极点问题转化为求解矩阵束的广义特征值问题。通过数学公式的演算与推导,在一定的程度上,矩阵束算法得到的极点与留数有比较高的精度。
2 极点与留数的变化关系
2.1 入射方向或观测的角度对极点与留数的影响
如图1,开槽圆环型的标签结构,其外圈的半径r1=20 mm,次外圈的半径r2=16 mm,最里圈的半径r3=9 mm,开槽的宽度依次等间距,其中宽度w=9 mm。如图1所示,对同一标签结构,入射波的极化方式一样(即极化的角度与入射传播方向成90度),考虑不同的入射方向激励标签结构,激励入射波与标签结构XOY平面之间的角度依次为90度,75度,60度,45度,30度,15度。

图1 不同的入射角度激励标签结构Fig.1 Angle of incidence of different excitation to tag structure
通过电磁波仿真软件FEKO,仿真得到其标签结构的RCS(Radar Cross Section)数据,运用矩阵束算法提取极点。如图2所示,在标签结构与入射波的极化角度相同的条件下,不同入射角度所得到的主要极点近似一样。
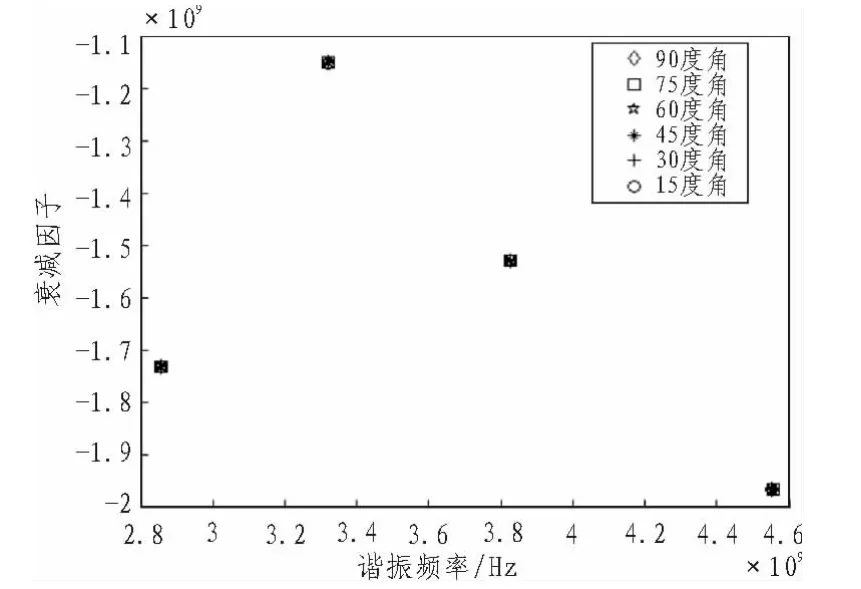
图2 不同入射角度的极点分布图Fig.2 Different incident angles of pole distribution
由开槽型结构所形成的谐振频率,与槽的长度成反比关系,槽的长度越长,所成的谐振频率值越小,相反,槽的长度越短,所形成的谐振频率值就越高。
由极点与结构的开槽数成对应映射关系,可以通过极点的个数与相应的谐振频率分布来设别标签的开槽数与开槽情况。
与极点相应得留数,如图3所示,在不同的入射角度下,留数呈现有规律的分布,随着入射的角度变化,依次的变化,其留数的绝对值越小。不难理解,入射的角度越大,其标签结构得到的散射信息的强度越低,而留数则可以表征这些极点幅度的强弱关系。

图3 不同入射角度时留数分布图Fig.3 Number of different angles of incidence of residue distribution
可以根据留数的相关信息可感知标签结构应对入射波或观测点的方位角度变化,进一步的对无芯片电子标签识别。
2.2 不同的极化角度,对标签结构的影响,极点与留数的关系
如图4所示,标签结构的尺寸与图1中的尺寸一致,图a,b,c分别表示在入射方向与标签结构的中心位置成45度角时,不同的入射波极化角度,依次的极化角度为0度,30度,90度。
从图5中大致的可以得到,在相同的标签结构,相同的入射角度的条件下,不同的入射极化角度,其极点分布情况也近似一致。通过理论仿真分析可以得到,这种开槽圆环型的标签结构,具有高度的对称性,入射波的入射的角度,与入射波的极化角度,对主要极点的分布影响不大,在理想环境下,可以近似为一样。
同样,与极点相应的留数,如图6所示,同样随着极化角度的变化而规律的变化,极化角度为0度时,相应的留数的值最小,极化角度为90度时,其留数的值最大。通过留数值的分布,反过来去感知标签结构相对于入射波的极化角度。这样可以通过留数值的变化情况,识别标签结构的极化特性。

图4 入射角度为45度时不同的极化角度Fig.4 Incident angle of 45 degrees angle of different polarization
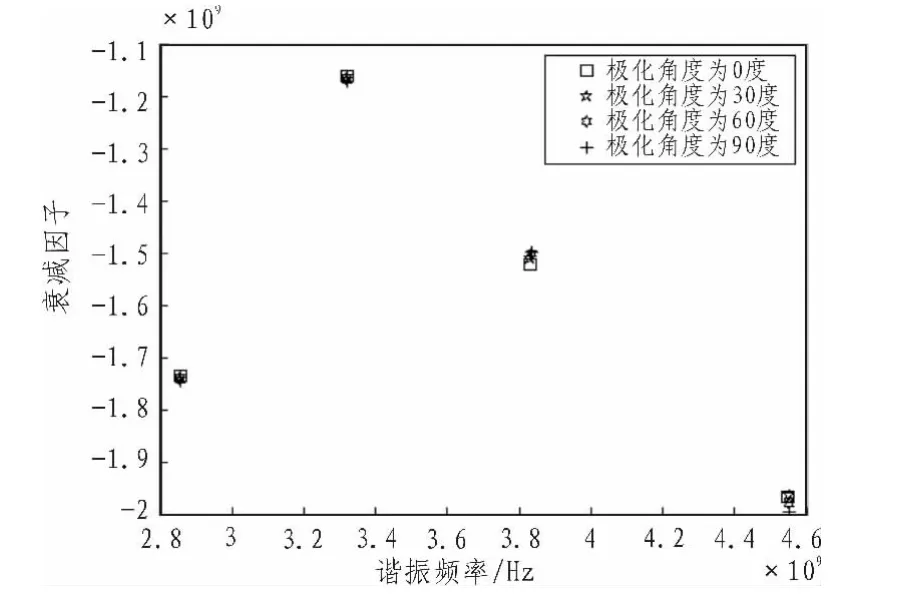
图5 入射角度为45度时不同极化角度的极点分布图Fig.5 When the incident angle is 45 degrees different polarization angles pole distribution
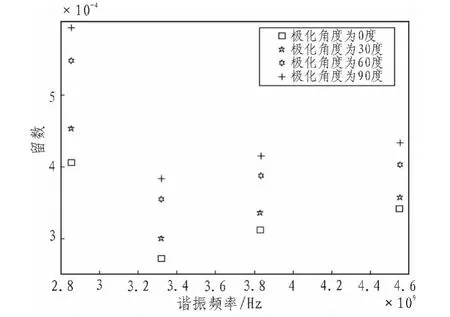
图6 入射角度为45度时不同极化角度的留数分布图Fig.6 When the incident angle is45 degrees different polarization angles residue distribution
2.3 弯曲形变的标签对极点留数的影响
如图7(a)所示,标签结构在弯曲曲率半径为30 mm的情况下的俯视图,(b)为侧视图。标签结构尺寸与开槽尺寸如图1所示。
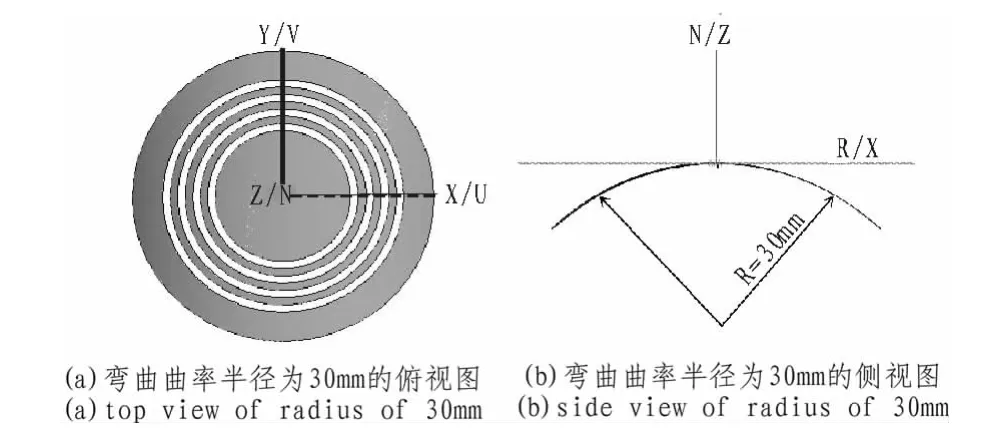
图7 弯曲型标签结构的示意图Fig.7 diagram strncture of bendable label
标签结构在不同的弯曲条件下,极点与留数分布情况,如图8图9所示。从图8中可以分析到,标签结构在不同程度上的弯曲,极点也会出现偏差而不同。由不同弯曲程度的标签结构,标签结构的基本属性也随之改变,极点中的衰减因子与谐振频率之间的关系则可恰好可表征标签结构的属性特征。
从图8可以得到,由于极点与留数共同表征信号,留数也随之有规律的变化,随弯曲半径的增多,其留数也随之变大。不难发现,平整平面时,标签结构接受到激励的有效单位面积越大,由RCS有关的定义与概念,其值与有效面积成正向关系,在散射场内,散射回的信号幅度越大。进而可以通过极点或留数的分布情况,识别与感知标签结构的弯曲程度。

图8 不同程度弯曲标签结构的极点分布图Fig.8 Varying degrees of bending the pole distribution label structure
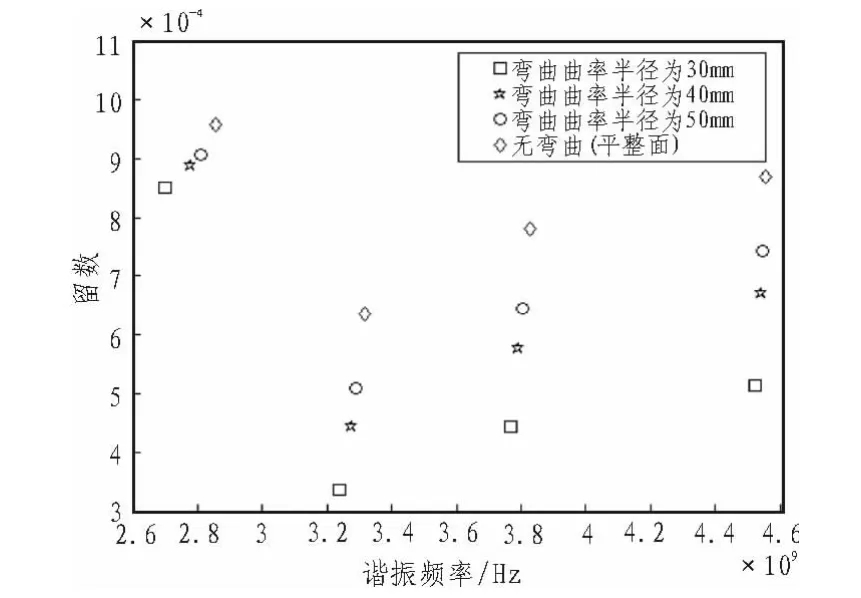
图9 不同程度弯曲标签结构的留数分布图Fig.9 Structure of varying degrees of bend label residue distribution
2.4 入射波的极化特性对弯曲型标签结构极点与留数的关系
对同一弯曲程度的标签结构(弯曲的曲率半径为30 mm时),相同的标签结构尺寸,相同入射波,不同的入射极化角度,由于结构的对称性,可依次取入射波的极化角度为0度,15度,30度,45度,75度,90度。

图10 弯曲半径为30 mm时极点分布图Fig.10 Pole distribution of bending radius of 30 mm
对同一弯曲程度的标签结构,极化角度的不同,极点与留数的分布情况如图10与图11所示,可以从图10中大致的分析到,对谐振频率在2.8 GHz附件的极点,在激励波的极化角度为45度左右时,其衰减因子的绝对值为最大,相应的留数也会随之变化,在激励波的极化角度为45度左右时,其留数的绝对值存在最大值,这表明变形的标签结构存在最佳激励波的极化角度。可以通过极点或者留数这种变化关系,感知弯曲型标签结构相对于入射波的极化特性。
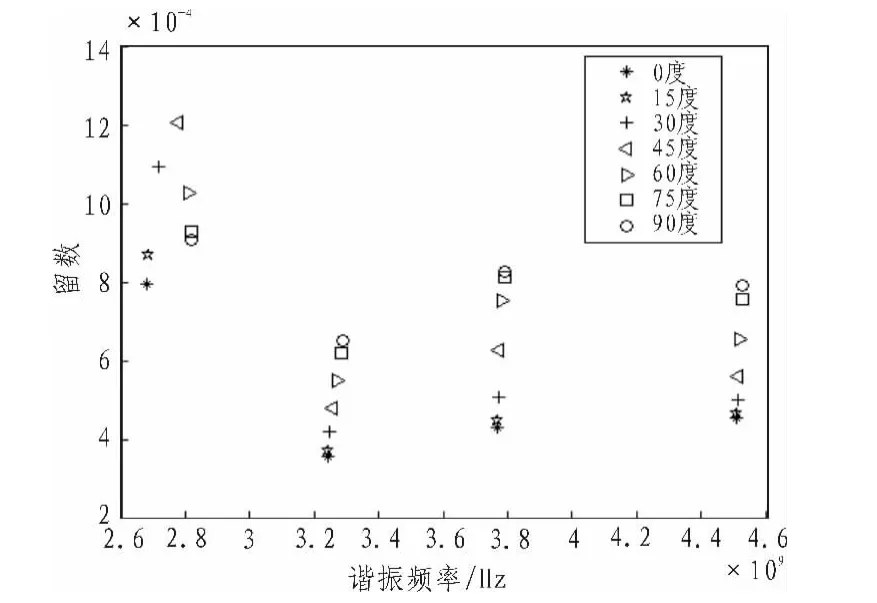
图11 弯曲半径为30 mm时留数分布图Fig.11 Residue distribution of bending radius of 30 mm
3 结束语
这种开槽圆环型的标签结构简单紧凑,还具有高度的对称性。通过极点的数据信息,可分析得到标签结构的基本属性,即开槽数以及开槽情况;还可以利用极点相对应的留数数据信息,感知标签结构的其它特征属性,即标签结构相对于入射波或者观测点的空间角度信息,标签结构的弯曲变形程度等。很大程度上,极点或留数还能够起到传感标签结构其它特性的作用。这种开槽圆环型的结构潜在成为一种具有感知传感功能的无芯片电子标签。
[1]KLAUS Finkenzeller,吴晓峰,陈大才译.射频识别技术[M].北京:电子工业出版社,2006.
[2]PRERADOVIC S,BALBIN I,KARMAKAR N C,et al.A novel chipless RFID system based on planar multiresonators for barcode replacement[C]//RFID,2008 IEEE International Conference on.IEEE,2008:289-296.
[3]ISLAM M A,KARMAKAR N.Design of a 16-bit ultra-low cost fully printable slot-loaded dual-polarized chipless RFID tag[C]//Microwave Conference Proceedings (APMC),2011 Asia-Pacific.IEEE,2011:1482-1485.
[4]VENA A,PERRT E,TEDJINI S.Chipless RFID tag using hybrid coding technique [J].Microwave Theory and Techniques,IEEE Transactions on,2011,59 (12):3356 -3364.
[5]JANG H S,LIM W G,OH K S,et al.Design of low-cost chipless system using printable chipless tag with electromagneti c code [J]. Microwave and Wireless Components Letters,IEEE,2010,20(11):640-642.
[6]PRERADOVIC S,KARMAKAR N C.Multiresonator based chipless RFID tag and dedicated RFID reader[C]//Microwave Symposium Digest (MTT),2010 IEEE MTT-S International.IEEE,2010:1520-1523.
[7]BAUM C E,ROTHWELL E J,CHEN K M,et al.The singularity expansion method and its application to target identification[J].Proceedings of the IEEE,1991,79 (10):1481-1492.
[8]SARKAR T K,PARK S,KOH J,et al.Application of the matrix pencil method for estimating the SEM(singularity expansion method)poles of source-free transient responses from multiple look directions[J].Antennas and Propagation,IEEE Transactions on,2000,48(4):612-618.
[9]王宝义,时振栋.电磁场在目标识别中的应用[M].北京:电子工业出版社,1995.
[10]BLISCHAK A T,MANTEDHI M.Embedded singularity chiplessRFID tags[J].Antennasand Propagation,IEEE Transactions on,2011,59(11):3961-3968.

