采用链路聚类的动态网络社团发现算法

董 哲，伊 鹏

（国家数字交换系统工程技术研究中心，450002，郑州）

社团作为复杂网络的重要特性受到了研究者的日益关注。社团将网络划分成许多由节点组成的群组，群组内部节点连接非常紧密而群组之间连接则较为稀疏。发现复杂网络中的社团结构具有很多重要的应用，如恐怖组织识别、网络舆情监控以及谣言的传播行为分析等。在动态网络中，由于其结构更加复杂，因此挖掘动态网络中的社团结构变得异常困难。

目前，关于复杂网络中的社团结构的研究已经取得了很多成果［1-3］。在现实生活中，绝大多数的网络都具有动态特性，这些网络随着时间的推移不断发生演化。虽然，这些变化对于网络的局部结构产生的影响较小，但随着时间积累网络中的社团结构会发生明显的变化，因此需要对其社团进行重新发现。目前，已经提出了许多动态网络社团发现算法。如Tang等人提出一种类似于语义迭代分析过程的算法［4］，发现动态多模网络中社团演化情况，该算法能够得到局部最优的社团结构，但是却需要人为指定社团个数，不能自适应地得到最优的社团结构。文献［5］提出了分析动态网络中社团的Social Cost算法，将社团发现转化为图着色问题，但该算法只关注特定个体的演化关系，不能从全局的角度来得到社团结构。还有其他一些动态社团发现算法，如：Gong等人提出一种基于局部搜索的多目标免疫算法［6］，但该算法复杂度非常大；Nguyen等人提出一种自适应增量算法QCA算法［7］，该算法只对发生变化的节点进行处理，能够得到较优的社团，但节点的变化情况复杂多变，导致算法的复杂度较大；文献［8］提出一种主题模型来发现网络中的社团结构，但是其算法的复杂度较大；文献［9］提出一种简单的增量社团发现算法，该算法复杂度较小，但是其算法精度较差；文献［10］提出了一种基于优化算法的动态社团发现方法，该算法避免了网络中离群点对算法的影响，提高了算法精度，但是其复杂度较大。

大多数社团结构发现方法是基于节点聚类的算法，难以发现稳定的社团。在网络中当节点存在交互关系时认为两节点间存在链路且唯一。因此，文献［11］提出一种基于链路的Link算法，该算法发现网络中稳定的社团具有明显的优势。算法首先对网络中的链路进行聚类，将得到的链路社团通过节点链路关系映射为节点社团［12］，但该算法无法发现动态网络中的社团结构。

针对上述问题，本文提出一种基于链路聚类的增量社团发现算法（link-based dynamic community detection algorithm，LDC）。该算法通过各个时刻的网络结构信息得到相关链路增量信息，再基于改进的链路划分密度函数（LD）对链路增量信息进行处理，以改进的链路模块度为目标函数，得到链路社团。为了验证算法的有效性，本文将其应用于人工动态网络和真实的动态网络中。实验证明，本文算法能够有效地发现具有典型动态信息网络中的多尺度稳定社团结构。

1 相关定义与指标

给定网络G（V，E），V 为节点集合，E为边集合，Ci为第i个社团节点集合。给出以下定义：定义1 节点时序图St表示t时刻个体间的关系，动态网络G可以用节点时序图的集合表示，T为时间段划分总数，G=（S1，S2，S3，…，St，…，ST），1≤t=G。

定义2 给定St，则链路图LG是St中节点间边的关系构成的链路集合，如图1所示。LG=｛0，1，2，3，4，5，6，7，8，9，10，11｝。

图1 链路图

定义3 给定链路L1和L2，L1=＜v1，v2＞，L2=＜v3，v4＞，其中v1、v2、v3、v4为节点。若L1∩L2=＜v1，v2＞∩＜v3，v4＞∅，则链路L2与L1互为邻链路。

定义4 给定t时刻链路社团Ci、Cj和链路L=＜v1，v2＞，若｛L|L∉Ci，L∉Cj，v1∈Ci，v2∈Cj，i≠j｝则L为桥链路。

1.1 链路划分密度

本文通过文献［11］中的链路划分密度D函数提出一种改进的链路划分密度函数DL处理增量信息。假定一个网络有M 条链路，｛P1，…，PC｝分别将网络划分成C个链路子集。定义社团的链路划分密度

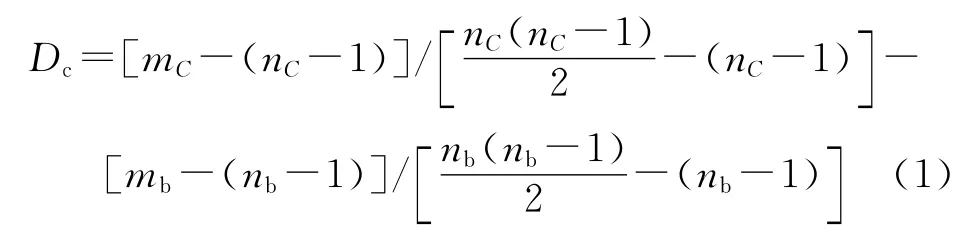
式中：mC=|PC|和为子集PC中链路数和节点数；mb表示社团之间的桥链路数；nb｝|表示社团之间的节点数。改进的链路划分密度，则

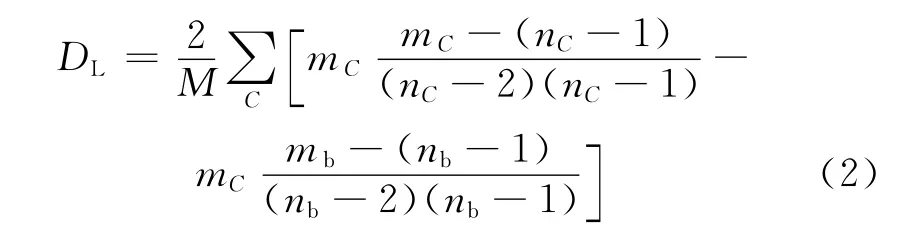
1.2 链路模块度

给出矩阵HN×M，N为网络中节点总数，M为网络中链路总数。如果链路l与节点i相关（i∈l），则H中的元素Hil=1，否则为0。令节点度ki=，表示与链路l相关的节点数，则模块度为

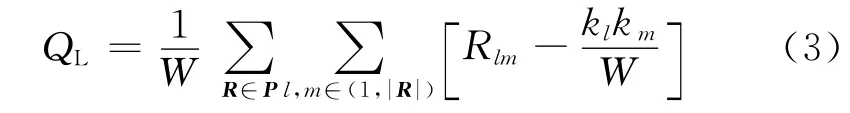
2 LDC动态社团发现算法

给定网络 G=（V，E），C=｛C1，C2，…，Ck｝，令动态网络中的增量信息为ε=｛ε1，ε2，…，εn｝。网络中的链路可分为2类：社团内部的链路（intracommunity links，IL），即边的2个端点均在该社团内；社 团 之 间 的 链 路 （bridge-community links，BL），即边的2个端点位于2个不同的社团内。对于G中的每一个社团C，当添加IL链路或者移除BL链路时使得社团的紧密性更强且网络结构更加清晰。相反，移除IL链路和添加BL链路使得网络结构渐渐模糊。当2个社团之间不存在干扰关系，或者干扰较小时，链路的增加或者移除有可能形成一个新的社团结构。因此，在更新社团结构时，网络结构的细微变化将会导致其社团产生巨大的变化。从链路的角度出发，通常随着时间的推移网络的变化其实就是链路的增加或移除。因此，网络中的变化信息就是一系列简单事件的集合，这些简单的事件包括新的链路的加入和已经存在的链路的移除等信息。

2.1 链路添加

当新增加一条链路e时，有2种情况：①链路e完全处于社团Ci内部；②链路e处于社团Ci和Cj之间，i≠j。对于情况①，根据定理1，社团结构保持不变。对于情况②，由定理2可知，如果桥链路e被划分进新的社团中，则该社团必为Ci和Cj之一。推论1给出了对桥链路e进行划分的判断条件，如果链路i或者j对应的链路划分密度变化值Δdi和Δdj均不满足，则不对该链路进行操作，具体见算法1。

算法1 添加边new-link

步骤1 输入新加入的链路e和t时刻链路社团结构Ct；

步骤2 输出t+1时刻链路社团结构Ct+1；

步骤3 若e是社团内部链路，则Ct+1≡Ct，否则k=arg max（Δdi，Δdj）并将e加入到Ck，更新Ct+1。

定理1 如果Ci是网络G中一个社团，那么添加任何一条IL链路到Ci，Ci不会分解成更小的模块。

证明 假设增量信息εi表示要添加一条内部链路e到社团Ci中，则Ci的链路划分密度为

令D′c表示e加入到社团Ci时的链路划分密度，则

令Δ=D′c-Dc，则Δ＞0，D′c＞Dc，故当加入内部链路e到Ci中后，社团更稳健。

定理2 如果添加的链路位于社团Ci和Cj之间，若该桥链路要被重新划分，则社团Ci和Cj为首选。证明 假设要添加的位于社团Ci和Cj之间的链路为e，则由于e的节点分别位于社团Ci和Cj中，所以当把链路e加入到其他社团时，DL值并不变。对社团Ci，链路e未加入时，相应链路前后对应的链路划分密度为

令Δ1=D′L，i-DL，i，则Δ1＞0，故链路e加入社团Ci之后，Ci的链路划分密度增大。同理，令Δ2=D′L，j-DL，j，Δ2＞0，Cj的链路划分密度也增大。

综上所述，如果添加的链路位于社团Ci和Cj之间时，则社团Ci和Cj为首选。

推论1 如果添加的桥链路e位于社团Ci和Cj之间，若满足条件Δd=DL，i（E+e）-DL，j（E+e）+DL，j（E）-DL，i（E）＞0，则桥链路e将被划分进社团Ci中，反之，桥链路e将被划分进社团Cj中。

证明 由定理2可知，如果添加的桥链路e位于社团Ci和Cj之间，Ci和Cj为其首选，则有

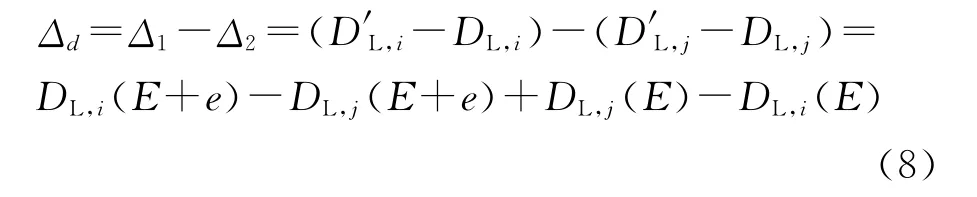
当Δd＞0时，Δ1＞Δ2，则桥链路e应被划分进社团Ci中；当Δd＜0时，Δ1＜Δ2，则桥链路e应被划分进社团Cj中。

2.2 链路移除

当某链路e被移除时，可分为2种情况：①该桥链路e处于社团Ci和Cj之间，i≠j；②该链路e完全处于社团Ci内部。依据推论3，对于情况①，移除桥链路时，社团不发生变化。

推论3 如果链路e为社团Ci和Cj之间的桥链路，当移除该链路时社团Ci和Cj结构更加明显，整体社团结构不变。

证明 当移除的链路e是社团Ci和Cj之间的桥链路时，社团内部节点间的链路关系未发生变化，而链路社团之间的链路被移除时，社团间的连接关系变得更稀疏，网络中的社团结构更加健壮、明显。因此，整体社团结构不会发生变化。对于情况②，当移除的链路e是一条IL链路时，令S（e）表示e的邻链路集合，∀l∈S（e），若Ck=argmax（DL，k（l）），则将链路l划分进社团Ck中，其中1≤k≤N，N为当前时刻的链路社团总数，具体见算法2。

算法2 移除边removal＿link

步骤1 输入被删除的链路e和t时刻链路社团结构Ct；

步骤2 输出t+1时刻链路社团结构Ct+1；

步骤3 若链路e是一条BL链路，则Ct+1≡Ct，否则Ck=arg max（DL，k（l）），l∈S（e）、k∈（1，N），并将链路l加入到社团Ck，更新Ct+1。

算法3给出了本文LDC算法的具体步骤。

算法3 LDC算法

步骤1 输入G=G0=（V0，E0），增量信息ε=｛ε1，ε2，…，εn｝；

步骤2 输出t时刻网络Gt的社团结构Ct；

步骤3 将节点图G0转化为链路图；

步骤4 发现初始时刻链路图社团结构C0；

步骤5 从初始时刻起，若e∈new＿link（L（u，v）），则new＿link（Ct，L（u，v）），否则removal＿link（Ct，L（u，v））；

步骤6 将链路社团结构Ct映射成为节点社团，得到各个时刻节点社团结构。

2.3 LDC算法的时间复杂度分析

如LDC算法所示，算法的步骤5虽然对所有时刻和变化的链路信息进行扫描，但之后的操作都是以步骤5作为判断条件的，如果条件不满足，就不会有后续操作。因此，运算中真正进行操作的遍数是εt的集合mi，即所有与增量信息有关的链路的数目。mi的大小与网络的时刻划分尺度有关，通过统计发现，网络中mi的规模为O（m），m为链路数。在步骤5添加边操作，每次循环有O（1）个单元操作，移除边操作需要O（lk）个单元操作，其中l为链路的邻链路数，k为社团个数，因此每一遍需要时间O（lk）。综合起来，总的算法时间复杂度为O（m x lk）。

3 仿真实验

为验证LDC算法的有效性，本节分别对人工动态网络和真实的动态社会网络数据集进行仿真实验。本文将LDC算法分别与Link算法［11］、GaoCD算法［12］、QCA 算 法［7］及 MIEN 算 法［13］进 行 比 较。Link算法从链路的角度发现网络中社团；GaoCD基于遗传算法，从链路的角度发现静态网络中重叠社团结构；QCA算法是基于节点的增量动态网络社团发现算法；MIEN算法通过压缩与解压缩，使用快速模块度算法更新网络中的社团。

3.1 人工网络

采用文献［14］的方法来生成人工数据集。该人工网络数据集共由128个节点组成，共4个社团，每个社团共有32个节点，如图2所示。同一社团内的节点对之间存在链路的概率为pin，不同社团的节点间存在链路的概率为pout，本文令pin=0.193 5，pout=0.020 8。

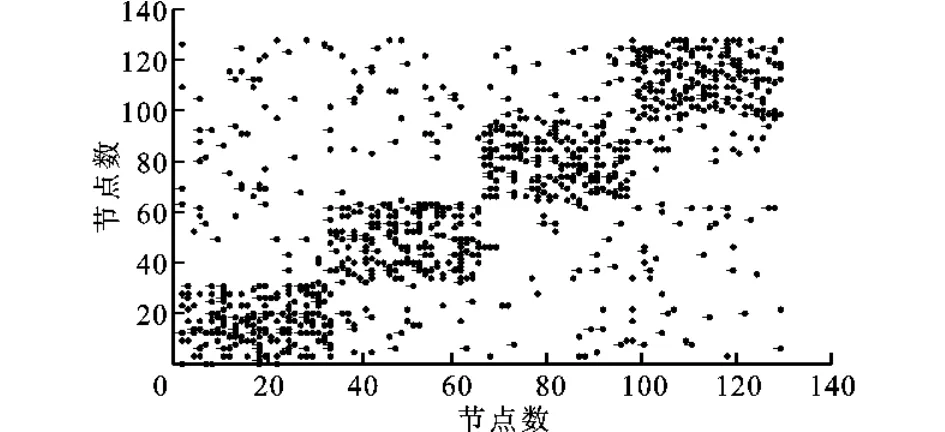
图2 具有128个节点4个社团结构的人工网络数据集

为了生成动态人工网络，在第一个时刻之后的每个时刻，随机选择10%的节点离开所属的社团，随机地加入到其他3个社团中。本文按照此方法生成10个时刻的人工网络。

将LDC算法应用于该数据集，仿真结果如图3所示。由图3a可知，在人工动态网络数据集中，本文提出的LDC算法其模块度要明显优于其他算法。由图3b可以看出，LDC算法发现的4个社团符合实际情况；由图3c可以看出，因为网络中的链路增量变化信息较少，所以LDC算法的运行时间相比于其他算法要少很多。标准化互信息值用来表征算法发现的社团结构与真实社团之间的差异，用于描述算法的准确性。由图3d可以看出，由于LDC算法只针对发生变化的链路信息进行处理，符合真实网络中社团的变化情况，所以其标准化互信息值要大于其他算法，提高了0.15。因此，LDC算法能够准确地发现网络中的社团结构。

图3 5种算法处理人工数据集的性能对比

3.2 真实网络

为了验证LDC算法在现实社会网络中的性能，本文采用了2种真实的社会网络数据集，分别是ENRON邮件网络［5］和 VAST数据集。ENRON邮件网络数据集来自ENRON公司内部的邮件联系网络，包含来自151名用户邮件消息的网络数据集，其时间跨度为1999年5月到2002年3月；VAST数据集来自IEEE VAST 2008，是一个开放的竞赛项目的数据集，它包含一组共400人10天的通话数据。

采用VAST数据集，以每一天为一个时间粒度，对比本文LDC算法和其他4种算法处理人工数据集的性能，结果如图4所示。

由图4a可以看出，相比于其他算法，LDC算法的链路模块度提高了20%；由图4b可见，LDC算法中发现VAST数据集中的社团更加稳定；由图4c可知，LDC算法的效率较高，算法性能优越；由图4d可知，相比于其他算法，LDC算法的标准化互信息值整体提高了0.13，LDC算法利用网络中的链路增量信息，能够发现更加准确的社团结构。

采用ENRON数据集，以每个月为一个时间粒度，对比本文LDC算法并和其他4种算法处理人工数据集的性能，结果如图5所示。

由图5a可以看出，LDC算法能够更有效地发现社团结构，相比于其他算法，LDC算法的链路模块度提高了19%；由图5b中可以看出，相比于其他几种算法，LDC算法得到的社团数目相对较多，这是由于该公司内部出现了一些变动，导致网络中的链路增量信息不完整导致了社团个数的增加，但同时说明LDC算法更倾向于发现具有多尺度、结构更加稳定的社团结构；图5c说明，LDC算法的运行效率要优于其他算法；由图5d可知，LDC算法的NMI值相比于其他算法要提高0.15，且要比其他算法稳定。

图4 5种算法处理VAST数据集对比

通过将LDC算法分别应用于人工网络和真实网络数据集中并和其他算法进行对比，由仿真结果可知，由于LDC算法是从链路的角度来发现动态网络中的社团，只对网络中的链路变化信息进行处理，简化了网络中的增量信息，相比于其他算法，LDC算法更能够准确地发现网络中稳定的社团结构。

图5 5种算法处理Enron数据集性能对比

4 结 论

本文提出一种基于链路聚类的动态社会网络社团发现算法——LDC算法，并提出了一种改进的社团划分密度，将复杂的动态网络中的变化信息简化为链路添加和链路移除2种增量信息，从链路的角度重新解决社团结构的发现问题。本文分别将LDC算法应用于人工动态网络和真实的动态社会网络中进行仿真实验，结果表明，与当前的动态网络社团发现方法相比，LDC算法能够快速准确地发现动态社会网络中稳定的多尺度社团结构。

［1］ 汪小帆.复杂网络中的社团结构分析算法研究综述［J］.复杂系统与复杂性科学，2008，5（3）：1-12.

WANG Xiaofan.An overview of algorithms for analyzing community structure in complex networks［J］.Complex Systems and Complexity Science，2008，5（3）：1-12.

［2］ 李晓佳，张鹏，狄增如，等.复杂网络中的社团结构［J］.复杂系统与复杂性科学，2008，5（3）：19-42.

LI Xiaojia.ZHANG Peng， DI Zengru，et al.Community structure in complex networks ［J］.Complex Systems and Complexity Science，2008，5（3）：19-42.

［3］ 陈国强，王宇平.采用离散粒子群算法的复杂网络重叠社团检测 ［J］.西安交通大学学报，2013，47（1）：107-113.

CHEN Guoqiang， WANG Yuping.Overlapping community detection of complex networks based on discrete particle swarm algorithm ［J］.Journal of Xi’an Jiaotong University，2013，47（1）：107-113.

［4］ TANG L，LIU H，ZHANG J.Identifying evolving groups in dynamic multimode networks ［J］.IEEE Transactions on Knowledge and Data Engineering，2012，24（1）：72-85.

［5］ TANTIPATHANANANDH C，BERGER-WOLF T，KEMNE D.A framework for community identification in dynamic social networks ［C］∥Proceedings of the 13th ACM International Conference on Knowledge discovery and Data Mining.New York，USA：ACM，2007：717-726.

［6］ GONG M G，ZHANG L J，MA J，et al.Community detection in dynamic social networks based on multiobjective immune algorithm ［J］.Journal of Computer Science and Technology，2012，27（3）：455-467.

［7］ NGUYEN N P，DINH T N，XUAN Y，et al.Adaptive algorithms for detecting community structure in dynamic social networks ［C］∥ Proceedings IEEE INFOCOM.Piscataway，NJ，USA：IEEE，2011：2282-2290.

［8］ LI D，DING Y，SHUAI X，et al.Adding community and dynamics to topic models ［J］.Journal of Informetrics，2012，6（2）：237-253.

［9］ 单波，姜守旭，张硕，等.IC：动态社会关系网络社区结构的增量识别算法 ［J］.软件学报，2009，20（1）：184-192.

SHAN Bo，JIANG Shouxu，ZHANG Shuo，et al.IC：incremental algorithm for community identification in dynamic social network ［J］.Journal of Software，2009，20（1）：184-192.

［10］BASSETT D S，PORTER M A，WYMBS N F，et al.Robust detection of dynamic community structure in networks［EB／OL］.［2013-03-14］.http：∥dx.doi.org／10.1063／1.4790830.

［11］AHN Y Y，BAGROW J P， LEHMANN S.Link communities reveal multiscale complexity in networks［J］.Nature，2010，466（7307）：761-764.

［12］SHI C，CAI Y，FU D，et al.A link clustering based overlapping community detection algorithm ［J］.Data＆ Knowledge Engineering，2013，87（1）：394-404.

［13］DINH T N，XUAN Y，THAI M T.Towards socialaware routing in dynamic communication networks［C］∥Proceedings of IEEE 28th International Conference on Performance Computing and Communications.Piscataway，NJ，USA：IEEE，2009：161-168.

［14］YANG T，CHI Y，ZHU S，et al.Detecting communities and their evolutions in dynamic social networks：a Bayesian approach ［J］.Machine Learning，2011，82（2）：157-189.