全球定位系统BLOCKⅡF星载原子钟性能评估

张清华，隋立芬，贾小林，肖国瑞

(1.信息工程大学 地理空间信息学院，郑州 450052；2.西安测绘研究所，西安 710054；3.地理信息工程国家重点实验室，西安 710054)

1 引言

原子钟是现代物理和电子技术的集大成者，其具有极高的频率准确度和稳定度，在航天和太空探索中得到广泛应用。全球卫星导航系统(global navigation satellite system， GNSS)以精确的时间测量为基础[1]，在轨运行的星载原子钟成为导航卫星极为重要的载荷，其性能会直接影响整个导航系统的精度、完好性和连续性等[2-3]，故对其进行准确的评估、对导航系统的建设和发展是一项有意义的工作。由于星载原子钟处于在轨运行状态，直接获取其频率数据比较困难，需采取其他手段，可以采用载波相位平滑伪距观测量对其特性进行分析，但测距码相位噪声和星上时间维持系统在很大程度上淹没了原子钟的特性[4-5]，而利用全球卫星导航系统国际服务协会(international global navigation satellite system service，IGS)钟差产品，即星载原子钟的精密钟差数据，则可以较好地分析原子钟的性能[6]，本文也将选取后一种数据进行评估。

关于对导航卫星星载原子钟的性能评估，国内外学者做了大量的研究。美国海军实验室(naval research laboratory，NRL)曾对所有全球定位系统(global positioning system， GPS)在轨卫星的性能进行过评估[7]，并在BLOCKⅡF发射前对其星载原子钟做了大量的评估实验[8-9]。文献[10]利用IGS的精密钟差产品，对2008年第四季度GPS在轨运行的星载原子钟的性能进行了评估。文献[11-12]针对导航卫星的时频特性分析的指标做了大量系统的研究。除了原子钟的基本性能，其预报性能也非常重要，导航电文中的钟差由短期预报得到[13]，长期预报则与卫星的自主导航性能有关[14]。关于预报的模型，国内学者针对长期预报和短期预报做了大量的研究[15-19]，得出二次多项式模型适用于短期预报，灰色模型适用于长期预报。综上所述，已有的研究成果在原子钟的性能评估从理论和实践上都有了一定的积累，为本文进行的评估实验奠定了一定的基础。但是，有关影响钟差预报精度的本质原因，并没有文献做出有针对性的分析，本文拟通过评估星载原子钟三个基本特性的基础上，通过相关分析来探索其与钟差预报精度的关系。

美国于2012-10-04发射了第三颗BLOCKⅡF卫星，并宣称有更长的使用寿命和更精确地原子钟[20]。由于关于BLOCKⅡA、BLOCKⅡR和BLOCKⅡR-M三类卫星的星载原子钟的性能已有较多的评估结果，故本文只对三颗最新的BLOCKⅡF卫星星载原子钟进行评估。

2 原子钟性能评估

图1 三种基本指标的关系

关于在轨卫星原子钟的性能评估，本文将从准确度、漂移率、稳定性和预报性能四个方面进行评估。其中前三个指标的概念比较明确，其关系如图1所示，关于钟的预报性能，本文在前人研究基础上，拟采取二次多项式模型进行短期预报，灰色模型进行长期预报。

2.1 准确度

原子钟的准确度是指其频率准确度，即实际输出频率与标称频率的相对偏差为

A=(fx-f)/f

(1)

式中，fx为测量频率，f为标称频率，A为原子钟的准确度。

2.2 漂移率

星载原子钟在轨运行过程中，受外界电磁环境的干扰以及自身的电子器件的老化，其输出频率一般会随在轨运行时间的增加而程单调变化，这种变化成为频率漂移率(老化率)。关于频漂率的计算，通常采用最小二乘解的形式表述为[12]

(2)

2.3 稳定性

表征原子钟频率稳定性常采用的方法为阿仑方差(Allan variance)和哈达玛方差(Hadamard variance)。

阿仑方差，又名双采样方差，最初该方法是用于分析振荡器的相位和频率不稳定性，后被美国电气和电子工程师协会(IEEE)标准定义为常用频率稳定性分析方法[12]，其定义式为

(3)

(4)

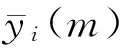
由于阿仑方差是一种双采样方差，频漂通常会对阿仑方差的估计产生影响，基于此，有人提出采用三次采样方差，即哈达玛方差来对原子钟的稳定性进行估计，其具有不受线性频漂影响的特性。其定义为

(5)

(6)

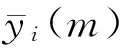
本文拟采用同时采用两种方差来对在轨卫星原子钟的稳定性做评估，并进行比较。

三是关于水功能区水质考核问题。对此项工作，省水利厅将按照2011年中央1号文件和国务院《关于实行最严格水资源管理制度的意见》要求，建立水功能区限制纳污制度。将积极与水利部和太湖流域管理局沟通衔接，确定好控制指标要求。同时将开展纳污总量管理，加快制定浙江省水功能区限制纳污指标体系和考核制度，促进包括太湖流域在内的全省水资源保护工作。目前，全省水功能区限制纳污指标分解和考核方案已完成初稿。强化入河排污口设置的审查管理，建立部门协作机制。进一步加强水资源监测能力建设，特别是加强《条例》确定的主要入太湖河道控制断面水资源监测能力建设，实行水功能区达标管理。

2.4 预报性能

通常情况下，假设钟差xj可由卫星钟读数T与系统时间t之间的关系表示，即钟差模型可以由下面的二次多项式拟合模型来表示

xj=T-t=a0+a1(tj-t0)+a2(tj-t0)2+ej

(7)

式中，a0、a1、a2分别为T相对于t0时刻、系统时间t的钟差、钟速和钟漂，ej为模型残差。根据最小二乘原理，三参数a0、a1及a2可由大量的钟差观测数据求出。

在建立灰色模型的过程中，首先要对钟差序列进行预处理，通常包括对数处理、方根处理、平移处理，通过这些变换得到一个新的适合灰色建模的序列用最小二乘法得到a，b后(a为发展系数，b为灰色作用量)，而灰色模型的预测值为

(8)

由式(8)的计算结果，再经过对数处理、方根处理、平移处理等的逆变换，就会得到x，则可以进行钟差的预报。

3 相关分析

变量之间的关系大致可归纳为两类，即函数关系和统计关系。关于钟的预报性能其实与以上三个性能都是有关的，但不是简单的函数关系，其受到多种因素的影响，这些关系不能用一个确定的数学式子描述，只能用统计关系来描述。相关分析是描述变量之间的变化关系一种统计学方法，对应的相关系数用以描述关系的密切程度。

本文采用典型皮尔逊(Pearson)简单相关分析来对在轨卫星钟三个基本特性和预报性能间的关系进行分析。典型Pearson简单相关系数计算公式为[22]

(9)

表1 不同相关系数值所表示的相关程度

4 算例分析

4.1 算例1

算例1对星载原子钟的性能进行评估，包含以下4个方面：1)准确度估计；2)漂移率估计；3)稳定度估计；4)预报性能评估，短期采用二次多项式模型，长期采用灰色模型。

三颗卫星准确度、漂移率和稳定性的统计可见表2，关于其长期和短期预报精度的统计结果见表3。图2和图3为PRN01星载原子钟相位和频率的。图4和图5PRN01星载原子钟的阿仑方差和哈达玛方差。(受篇幅所限，对于相位和频率图、阿仑方差和哈达玛方差图，文中只给出PRN01卫星的结果)。

对于钟差预报，短期预报采用1 d，长期预报分为1～30 d和1～100 d，值得注意的是，PRN05卫星由于在轨运行时间比较短，其没有积累100 d的精密钟差数据，故长期预报采用1～30 d。

图2 PRN01的相位数据

图3 PRN01的频率数据

图4 PRN01的阿仑方差

图5 PRN01的哈达玛方差

卫星号准确度(10-12)漂移率(10-15s/d)稳定度(10-14s/d)PRN011.439.030.43PRN052.533.174.10PRN250.875.153.58

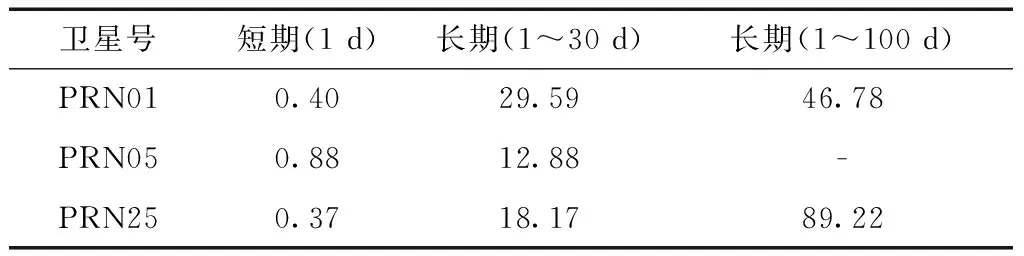
表3 不同尺度上的预报精度/ns

由算例1可以得到如下结论：

1)由图2及图3可知，导航卫星的钟差数据(相位)随时间的增加呈现一个近似线性的关系，故在较短的尺度内二次多项式模型可以很好地反映这种特性，导航卫星的频率数据存在一定程度上的漂移；

2)对比图4及图5可以发现，在较短尺度上评估稳定性，两种方差有相近的结果，但随着时间尺度的增大，线性频漂通会对阿仑方差的估计产生了一定影响，而哈达玛方差不受线性频漂的影响，由于三颗卫星采用的铷钟存在一定的线性频漂，故采取哈达玛方差比较合适；

3)由表2及表3可以得到在轨原子钟的性能指标：准确度在10-12量级，每天的漂移率在10-15s量级，每天的稳定性在10-14量级，短期(1 d)预报精度优于1 ns，长期预报精度分别优于30 ns(1～30 d)和90 ns(1～100 d)。

4.2 算例2

针对以上评估得到的卫星钟性能，下面来分析准确度、漂移率、天稳和短期(1 d)预报、长期(1～30 d)、长期(1～100 d)的相关关系。在分析的过程中，采取了多组数据来进行分析，并最终取平均值，以增加相关分析的可靠性。图6和表4反映了相关分析的结果。

图6 预报精度与三个钟性能指标的相关性

预报长度短期(1d)长期(1～30d)长期(1～100d)准确度0.79-0.17-0.31漂移率-0.260.69-0.24稳定性0.180.550.57

由算例2可以得到如下结论：

1)在短期(1 d)预报中，其精度与准确度显著相关，与漂移率和稳定性微相关；

2)在长期(1～30 d)预报中，其精度与漂移率和稳定性显著相关，与准确度微相关；

3)在长期(1～100 d)预报中，其精度与稳定性显著相关，与准确度低度相关，与漂移率微相关。

5 结束语

本文针对GPS最新型号的BLOCKⅡF卫星，不仅估计了其星载原子钟的三个常规性能，还分别估计了其长期和短期预报性能。在此基础上，用相关分析的方法，探索了星载原子钟钟差预报精度和三个常规性能之间的关系，得到了一些初步的结论，为进一步研究提供一些有益参考。

[1] KAPLAN E D，HEGARTY C J.Understanding GPS：Principles And Application[M].2nd ed.Norwood， MA：Artech House Publisher，2006.

[2] WEISS M，SHOME P，BEARD R.On-board GPS Clock Monitoring for Signal Integrity[EB/OL].[2013-10-25].http：//tf.nist.gov/general/pdf/2492.pdf.

[3] LEE S， KIM J， LEE Y.Protecting Signal Integrity Against Atomic Clock Anomalies on Board GNSS Satellites [J].IEEE Transactions on Instrumentation and Measurement， 2011，60(7)：2738-2745.

[4] PETZING J， REITH R，DASS T.Enhancements to the GPS Block IIR Rubidium Timekeeping System[EB/OL].[2013-10-25].www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA485237.

[5] REID W，MCCASKILL T，LARGAY M， et al.Performance of GPS Block IIR Rubidium Clocks[C]//Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000).Salt Lake City：[s.n.]，2000：937-946.

[6] SENIOR K L，RAY J R，BEARD R L.Characterization of Periodic Variations in the GPS Satellite Clocks[J].GPS Solution， 2008(12)：211-225.

[7] OAKS J，BUISSON J A.A Summary of the GPS Constellation Clock Performance[EB/OL].[2013-10-25].http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA485348.

[8] VANNICOLA F， BEARD R，WHITE J， et al.GPS BLOCK IIF Atomic Frequency Standard Analysis[C]//Proceedings of the 42nd Annual Precise Time and Time Interval Systems and Applications Meeting.Reston， Virginia：[s.n.]，181-196.

[9] VANNICOLA F， BEARD R，WHITE J， et al.GPS Block IIF Rubidium Frequency Standard Life Test[EB/OL].[2013-10-25].http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA518066.

[10] 贾小林，冯来平，毛悦，等.GPS星载原子钟性能评估[J].时间频率学报，2010，33(2)：115-121.

[11] 郭海荣，杨元喜.导航卫星原子钟时域频率稳定性影响因素分析[J].武汉大学学报：信息科学版.2009， 34(2)：218-221.

[12] 郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州：信息工程大学测绘学院，2004.

[13] GUO Chang-xu.GPS Theory， Algorithms and Applications [M].2nd ed.Berlin：Springer， 2007：76-77.

[14] ANANDA M P，BERNSTEIN H， CUNNINGHAM K E，et al.Global Positioning System (GPS) Autonomous Navigation [C]//Proceedings of Location and Navigation Symposium.Las Vegas， Nevada：IEEE， 1990：497-508.

[15] 崔先强，焦文海.灰色系统模型在钟差预报中的应用[J].武汉大学学报：信息科学版，2005，30(5)：447-450.

[16] 张清华，隋立芬，贾小林.应用Jones-Tryon Kalman滤波器对在轨GPS Rb钟进行状态监测[J].武汉大学学报：信息科学版，2012，37(4)：436-440.

[17] STEIN S R， EVANS J.The Application of Kalman Filters and ARIMA Models to the Study of Time Prediction Errors of Clocks for Use in the Defense Communication System (DCS) [C]//Proceedings of the 44th Annual Symposium on Frequency Control.Baltimore：[s.n.]， 1990：630-635.

[18] LEE A B.A Kalman Filter for Atomic Clocks and Timescales[EB/OL].[2013-10-25].http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA485679.

[19] SENIOR K.Report of the IGS Clock Products Working Group[EB/OL].[2013-10-25].http：//www.bipm.info/utils/common/documents/tai_2004/Doc_15.pdf.

[20] Boeing.Global Positioning System (GPS) IIF[EB/OL].[2013-10-25].http：//www.boeing.com/boeing/defense-space/space/gps/.

[21] EEE Standard 1139-1999，EEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology-Random Instabilities[S].

[22] ANDERSON T W.多元统计分析导论[M].张润楚，译.3版.北京：人民邮电出版社，2010.